ГлавнаяРазное2 x область определения

Область определения и множество значений. 2 x область определения


Область определения и множество значений

$ |x| = \begin{cases} x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \\ -x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x А графиком является

Свойства:

1) $|x| \geq 0$ 2) $|x|=0 \longleftrightarrow x=0$ 3) $|xy|=|x||y|$ 4) $|x+y| \leq |x|+|y|$ 5) $||x||=|x|$ 6) $|-x|=|x|$ 7) $|x-y|=0 \longleftrightarrow x=y$ 8) $|x-y| \leq |x-z|+|z-y|$ 9) $|\dfrac{x}{y}|=\dfrac{|x|}{|y|} \,\,\,\,\, y \neq 0$ 10) $ ||x|-|y|| \leq |x-y|$

Для того, чтобы найти область определения и множество значений функции, состоящей из абсолютных значений, необходимо учитывать вышеуказанные свойства. Пример:Найти область определения и множество значений $f(x)=\dfrac{x+2}{|x|-2}$ Решение:

$|x|-2=0 \rightarrow |x|=2 \rightarrow x=\pm 2$

Таким образом

$D_f=\mathbb{R} - \lbrace \pm 2 \rbrace$

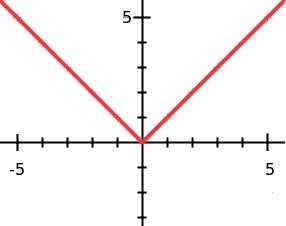
С другой стороны $f(x)=\dfrac{x+2}{|x|-2}= \begin{cases} \dfrac{x+2}{x-2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x \geq 0 \\ \\ \dfrac{x+2}{-x-2}=-1 \,\,\,\,\,\,\,\,\, x So

$x \geq 0 \rightarrow y=\dfrac{x+2}{x-2} \rightarrow x=\dfrac{2(y+1)}{y-1} \geq 0$

Следовательно $\begin{cases} x \geq 0 \,\,\,\,\,\,\,\, y\in (-\infty,-1] \cup (1,+\infty) \\ \\ x

$\rightarrow R_f=(-\infty,-1] \cup (1,+\infty)$

Вот график $f$ Пример: Найти область определения и множество значений $f(x)=\dfrac{1}{\sqrt{|x+1|-4}}$. Решение: $|x+1|-4 >0 \,\, \rightarrow|x+1|>4 \rightarrow$ $\begin{cases} x+1>4 \rightarrow x>3 \\ x+1

$D_f=(-\infty,-5) \cup (3,+\infty)$

Отметим, что

$y=\dfrac{1}{\sqrt{|x+1|-4}}>0$

С другой стороны

$y^2=\dfrac{1}{|x+1|-4} \rightarrow |x+1|=\dfrac{1}{y^2}+4>4 \rightarrow \dfrac{1}{y^2}>0 \rightarrow y \in (-\infty,0)\cup(0,+\infty)$

Следовательно

$y \in (\mathbb{R}-\lbrace 0 \rbrace ) \cap ( \mathbb{R} ^+ )$

Значит

$R_f=(0,+\infty)=\mathbb{R}^+$

Вот график $f$
Упражнения
Найти область определения и множество значений.

1) $y=\dfrac{x}{|x-1|}$ 2) $y=\dfrac{x-4}{|x|-4}$ 3) $y=\dfrac{\sqrt{\sqrt{(x+1)^2}-1}}{\sqrt{|x+1|-1}}$ 4) $y=\dfrac{\sqrt{(x-1)^2}}{x-1}$ 5) $y=\sqrt{-|x+1|}$ 6) $y=\dfrac{\sqrt{(x^2-3x+2)^2}}{\sqrt{(x-2)^2}}$ 7) $y=|x-1|+|x|+|x+1|$

Общий вид показательной функции $y=a^{u(x)}$, где $a>0$, а $u(x)$ - функция. Нахождение области определения и множества значений показательной функции зависит от $u(x)$. В специальном виде, если $a=e \simeq 2.71828\cdots$, то $y=e^{u(x)}$. Для лучшего понимания $y=a^{u(x)}$ его можно переписать как $y=e^{u(x)\log_e a}$. Отметим, что $\log_e a$ обозначается как $\ln a$. Следовательно,

$y=e^{u(x)\ln a}$

Согласно этому определению $a>0$ является достаточным условием для определения показательной функции, если $u(x)$ вещественная функция.

Совет:

$y=e^x=\lim_{n \rightarrow \infty} (1+\dfrac{1}{n})^nx=1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots\,\,\,\,\, (n \in \mathbb{N})$

Пример:Найти область определения и множество значений $f(x)=2^{-x^{-2}}$. Решение:Отметим, что если $x=0$, то знаменатель дроби неопределен. Следовательно,

$D_f=\mathbb{R}-\lbrace 0 \rbrace$

Определим множество значений: Для начала отметим, что $y>0$. С другой стороны

$\log y=-\dfrac{1}{x^2}\log 2 \rightarrow x^2=-\dfrac{\log 2}{\log y} \rightarrow x=\pm \sqrt{-\dfrac{\log 2}{\log y}} \rightarrow \dfrac{\log 2}{-\log y}>0 \rightarrow$

$ \log y 0 \rightarrow 0 Значит

$R_f=(0,1)$

График этой функции

Пример:Найти область определения и множество значений $f(x)=3^{-x}$. Решение:Очевидно, что $D_f=\mathbb{R}$. С другой стороны

$y=\dfrac{1}{3^x} \rightarrow 3^x=\dfrac{1}{y} \rightarrow x=\log_3 \dfrac{1}{y}$

$R_f= \lbrace y| y \in \mathbb{R},\dfrac{1}{y}>0 \rbrace = \lbrace y \in \mathbb{R} | y>0 \rbrace =(0,+\infty)$

$R_f=\mathbb{R^+}$

График $f$
Упражнения
Найти область определения и множество значений.

1) $y=e^{-\dfrac{1}{\sqrt{x-\lfloor x \rfloor}}}$ 2) $y=3^{\dfrac{\sqrt{8}}{2}}$ 3) $y=5^{-x^2}$ 4) $y=5^{\lfloor x \rfloor + \l

www.math10.com

Как найти область определения функции???

При решении многих задач приходится искать область определения функции. Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним.

И так, область определения функции – это множество всех тех значений переменной х, при каких функция f(x) имеет смысл. То есть значения переменной х, при которых функция от этой переменной существует, а могут быть и такие, при каких она не существует, нам нужны, только те, при которых – существует.

Рассмотрим конкретные варианты, в каких случаях функция может существовать не при всех значениях переменной:

Я постарался собрать самые основные случаи, когда область определения функции – это не все вещественные числа. Конечно, примеры могут быть на много сложнее, потому что даже эти четыре варианты можно так скомбинировать, что на то что бы разобраться, что там и от чего зависит, пойдёт не мало времени. И ещё, я даже не все перечислил.

Материалы по теме:

Поделиться с друзьями:

Загрузка...

matemonline.com

Область определения и множество значений

Автор: Sepehr Hassannejad

Часть 2

Определение:Множество первых элементов пары $f$ называется областью определения, а множество вторых элементов называется множеством значений. Область определения и множество значений функции обозначаются как $D_f$ и $R_f$ соответственно. Математическим языком

$D_f=\lbrace x |(x,y) \in f \rbrace$ $R_f= \lbrace y | (x,y) \in f \rbrace $

Пример:Пусть $f=\lbrace (1,-1),(3,3),(7,-1),(5,3) \rbrace$. Определить $D_f$ и $R_f$. Решение:

$D_f=\lbrace 1,3,5,7 \rbrace$ $R_f= \lbrace -1,3 \rbrace$

Пример:Если $D_f=R_f=\lbrace 1,2,3 \rbrace$, то сколько разных функций можно составить с данной областью определений и множеством значений? Решение:

$f=\lbrace (1, \bigcirc ),(2 , \bigcirc),(3,\bigcirc) \rbrace$

Первую позицию можно заполнить 1, либо 2 или 3, следовательно существует три способа заполнения первой позиции. Вторую позицию можно также заполнить тремя разными способами. Значит существует $ 3 \times 3 \times 3=27$ способов. Это означает, что есть 27 разных функций, у который будут данные $D_f$ и $R_f$. Некоторые из них указаны ниже. Можно также доказать ответ, написав все возможные решения.

$f_1 = \lbrace (1,1),(2,2),(3,3) \rbrace$ $f_2 = \lbrace (1,1),(2,1),(3,1) \rbrace$ $f_3 = \lbrace (1,1),(2,3),(3,2) \rbrace$

Если $f$ определена множеством пар или таблицей, тогда область определения и множество значений четко определены.

Пример:Найти область определения и множество значений у $f=\lbrace (1,4),(2,5),(3,6) \rbrace$. Решение:

$D_f=\lbrace 1,2,3 \rbrace \,\,,\,\, R_f= \lbrace 4,5,6 \rbrace$

Математически

$D_f= \lbrace x | x \in \mathbb{N} , 1 \leq x \leq 3 \rbrace$

$R_f= \lbrace x | x \in \mathbb{N} , 4 \leq x \leq 6 \rbrace$

Пример:Найти область определения и множество значений у $f=\lbrace (1,1),(2,3),(3,5),(4,7),(5,9),(6,11),(7,1),(8,7),(9,8),(10,9),(11,10) \rbrace$. Затем определить функцию. Решение:

$D_f=\lbrace 1,2,3 , \cdots ,11 \rbrace = \lbrace x| x \in \mathbb{N} , x \leq 11 \rbrace$

$R_f= \lbrace 1,3,5,7,8,9,10,11 \rbrace$

$f(x)= \begin{cases} 2x-1 \,\,\,\,\,\,\,\,\,\,\,\, x \leq 6 \,\,\,\, x \in \mathbb{N}\\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=7\\ x-1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 1 \leq x \leq 8 \,\,\,\, x \in \mathbb{N} \end{cases}$

Пример:Найти область определения и множество значений указаной ниже кусочно-заданной функции. Затем задать ее множеством пар и начертить ее график. $f(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0\\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0\\ -1 \,\,\,\,\,\,\,\,\,\,\,\, x Решение: Очевидно, что

$D_f= \mathbb{R} \,\,,\,\, R_f= \lbrace -1,0,1 \rbrace $

$f(x)=f_1 \cup f_2 \cup f_3= \begin{cases} f_1 = \lbrace (x,y) | x \in \mathbb{R^+} \,\,,\,\, y=1 \rbrace \\ f_2 = \lbrace (0,0) \rbrace \\ f_3 = \lbrace (x,y) | x \in \mathbb{R^-} \,\,,\,\, y=-1 \rbrace \end{cases}$

Совет: Эта функция также называется кусочно-постоянная функция и обозначается как $\textit{Sgn(x)}$. $Sgn(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0 \\ -1 \,\,\,\,\,\,\,\,\,\,\,\, x
Упражнения
Найти область определения и множество значений функций. 1) $f(x)= \begin{cases} 3 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>1 \\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=1 \\ -3 \,\,\,\,\,\,\,\,\,\,\,\, x

2) $g(x)= \begin{cases} -1 \,\,\,\,\,\,\,\,\,\,\, x0 \end{cases} $

3) $h(x)= \begin{cases} -2 \,\,\,\,\,\,\,\,\,\,\,\,-2 4 \end{cases} $

4)$k(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x\geq 2 \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x Полиномиальная функция Определение:$f$ называется полиномиальной функцией тогда и только тогда, если для каждого действительного значения $x$ ($x \in \mathbb{R}$)

$f(x)=a_n x^n+a_{n-1} x^{x-1}+\cdots+a_1 x+a_0 \,\,\,\,\,\,\,\, n \in \mathbb{N} \cup \lbrace 0 \rbrace$

$a_0,a_1,\cdots,a_n$, принимающие действительные значения, называют коэффициентом полинома, а неотрицательные целые значения $n$ если $a_n \neq 0$ называют степенью полинома. Область определения полиномиальной функции $\mathbb{R}$. Для определения множества значений полиномиал

www.math10.com

Как найти область определения функции y=2x+3

1)Область определения функций определяется как нахождение всех допустимых значеий х, и имеет некоторые ограничения. а. Если определяемая функция нахолится в знаменателе дроби, но значение функции не должно равняться нулю. б. Если определяемая функция находится под знаком корня, то её значение должно быть больше или равно 0. В данной функции нет знаменателя или корня, поэтому область определения функции имеет бесконечное множетво чисел. 2)Область значений- все значения переменной y 3) эта функция имеет общий вид y=kx+b. График-прямая.

Область определения функции это интервал на котором функция у=2х+3 имеет смысл... а область значения это множество чисел состоящее из всех значений функций.. ну в теории плохо понятно.. допустим на твоем примере.. у=2х+3 это прямая... она определена везде.. т. е область определения х принадлежит от минус бесконечности до плюс бесконечности и также область значений только y принадлежит от минус бесконечности до плюс бесконечности... а если взять у=корень (х-5).. то смотрите это функция имеет смысл только когда подкоренное выражение больше или равно нуля... т. е. х-5>=0 ; x>=5..Т. е. получается область определения от 5 до плюс бесконечности... А область значений.. это какие значения принимает у при х от 5 до бесконечности.. и получается что у принимает только положительные значения... т. е. у принадлежит от 0 до плюс бесконечности..

1 ???Это школа? Спроси учителя своего лучше, чем больше будешь узнавать про функции, тем более бедет усложняться алгоритм их решений (или я не поняла вопроса?? ) 2 Область определений - какие значения может принимать переменная в данной функции, в твоем случае функция определена на всей числовой прямой, а вот если бы у тебя была функция, например, y=1/x, то функция была бы не определена в точке х=0, потому что x здесь стоит в знаменателе и не может обращаться в 0 (на 0 делить нельзя) Область значений - какие значения может принимать функция (проще говоря чему равен y или f(x) ), в твоем случае опять же область значений от минус бесконечности до плюс бесконечности, а к примеру y=x^2 область значений от нуля до плюс бесконечности (потому что любое значение х при возведении в квадрат даст положительный у) 3 функции типа f(x)=kx+c, (k и c - числа) - всегда задают прямую

touch.otvet.mail.ru

Подскажите,как найти область определения функции y=1/x^2-x (после палочки в корне)?

Поскольку даная функция — дробь, то её знаменатель не должен быть равным нулю. Т. е. x^2-x ≠ 0 x(x-1)≠0 => x≠0, x≠1 Итого область определения функции включает в себя всё множество действительных чисел без 0 и 1: x є (-oo, 0)U(0,1)U(1, +oo)

Функция как то не понятная вы хоть бы скобочки использовали и что такое (после палочки в корне) ? x^2-x - это полностью знаменатель? если так то От минус бесконечности до плюс бесконечности Х не равно 0

Вообще надо просто найти все элементарные функции, из которых состоит заданная функция и найти х при которых у них допустимые аргументы. Пересечение этих множеств - будет область определения всей функции. Если есть дробь - её знаменатель не должен равняться 0. Если есть корень - выражение под ним должно быть неотрицательно ( >= 0 ) Если есть логарифм - выражение под ним (и его основание) должно быть положительным. Так что в данном случае надо решить неравенство (x^2-x) >= 0 (если там дроби нет) Решай. (З. Ы. Ну и записывать рекомендую иначе - лучше корень (x^2-x) или что-то в этом роде. ) &gt^.^&lt

touch.otvet.mail.ru

Область определения функции — Википедия РУ

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

где R{\displaystyle \mathbb {R} }  и C{\displaystyle \mathbb {C} }  — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции f(x)=x{\displaystyle f(x)=x}  совпадает с областью отправления (R{\displaystyle \mathbb {R} }  или C{\displaystyle \mathbb {C} } ).

Гармоническая функция

Область определения функции f(x)=1/x{\displaystyle f(x)=1/x}  представляет собой комплексную плоскость без нуля:

domf=C∖{0}{\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}} ,

поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.

Дробно-рациональные функции

Область определения функции вида

f(x)=a0+a1x+⋯+amxmb0+b1x+⋯+bnxn{\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}} 

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

b0+b1x+⋯+bnxn=0{\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0} .

Эти точки называются полюсами функции f{\displaystyle f} .

Так, например, f(x)=2xx2−4{\displaystyle f(x)={\frac {2x}{x^{2}-4}}}  определен на всех точках, где знаменатель не обращается в ноль, то есть, где x2−4≠0{\displaystyle x^{2}-4\neq 0} . Таким образом domf{\displaystyle \mathrm {dom} \,f}  является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть F={f∣f:X→R}{\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}}  — семейство отображений из множества X{\displaystyle X}  в множество R{\displaystyle \mathbb {R} } . Тогда можно определить отображение вида F:F→R{\displaystyle F\colon \mathbb {F} \to \mathbb {R} } . Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x0∈ X{\displaystyle x_{0}\in ~X} , то можно определить функцию F(f)=f(x0){\displaystyle F(f)=f(x_{0})} , которая принимает в «точке» f{\displaystyle f}  то же значение, что и сама функция f{\displaystyle f}  в точке x0{\displaystyle x_{0}} .

http-wikipediya.ru

Область определения Википедия

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Определение

Если на множествеX{\displaystyle X} задана функция, которая отображает множество X{\displaystyle X} в другое множество, то множество X{\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: f:X→Y{\displaystyle f\colon X\to Y}, то

Иногда рассматривают функции, определенные на подмножестве D{\displaystyle D} некоторого множества X{\displaystyle X}. В этом случае множество X{\displaystyle X} иногда называют областью отправления функции f{\displaystyle f}[3].

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

где R{\displaystyle \mathbb {R} } и C{\displaystyle \mathbb {C} } — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции f(x)=x{\displaystyle f(x)=x} совпадает с областью отправления (R{\displaystyle \mathbb {R} } или C{\displaystyle \mathbb {C} }).

Гармоническая функция

Область определения функции f(x)=1/x{\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:

domf=C∖{0}{\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}},

поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.

Дробно-рациональные функции

Область определения функции вида

f(x)=a0+a1x+⋯+amxmb0+b1x+⋯+bnxn{\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

b0+b1x+⋯+bnxn=0{\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0}.

Эти точки называются полюсами функции f{\displaystyle f}.

Так, например, f(x)=2xx2−4{\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x2−4≠0{\displaystyle x^{2}-4\neq 0}. Таким образом domf{\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть F={f∣f:X→R}{\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}} — семейство отображений из множества X{\displaystyle X} в множество R{\displaystyle \mathbb {R} }. Тогда можно определить отображение вида F:F→R{\displaystyle F\colon \mathbb {F} \to \mathbb {R} }. Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x0∈ X{\displaystyle x_{0}\in ~X}, то можно определить функцию F(f)=f(x0){\displaystyle F(f)=f(x_{0})}, которая принимает в «точке» f{\displaystyle f} то же значение, что и сама функция f{\displaystyle f} в точке x0{\displaystyle x_{0}}.

См. также

Примечания

Литература

wikiredia.ru