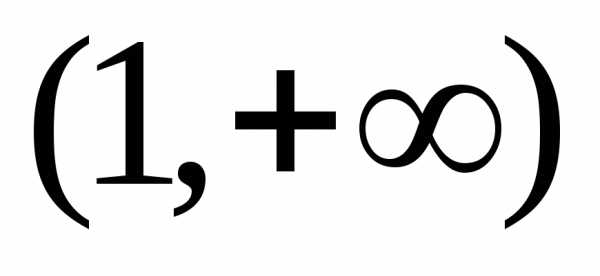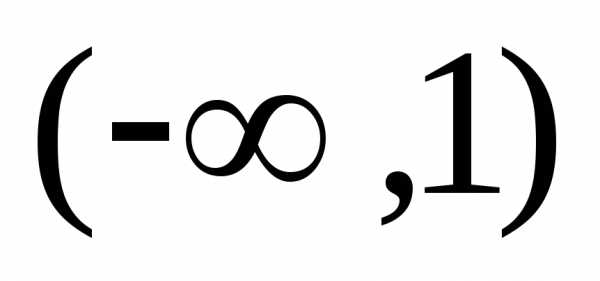7.4. Выпуклость, вогнутость графика функции, точки перегиба. Абсциссами точек перегиба графика y x3 функции являются
4.4. Выпуклость графика функции. Точки перегиба

y ' = 1 (a – 2x )2 +x 2(a – 2x )(-2)= (a – 2x )(a – 2x – 4x )=
= ( a – 2x )(a – 6x ).
Находим критические точки. Производная равна нулю при x 1 =а2 иx 2 =а6 .
Находим значения функции в критических точках и на концах отрезка:
| а |
| а | 2 | a 3, f(0) = 0. |
|
| |||||
f |
| = 0; | f |
| = |
|
| |||||
|
| 27 |
|
| ||||||||
| 2 |
| 6 |
| а |
|
| 2 |
| |||
Итак, наибольшее значение функции M = f |
| = | a 3. | |||||||||
|
|
|
|
|
|
| 6 |
|
| 27 |
| |
Если сторона вырезаемых квадратов x =а6 , получим короб-
ку наибольшего объёма
y = 2 a3.
27
Определение. График дифференцируемой функции
y = f(x) называется выпуклым вверхна интервале (а, b),если все точки графика лежат ниже любой касательной к графику функции на этом на интервале (рис. 28). График дифференцируемой функции y = f(x)называется выпуклым внизна интервале (а, b),если все точки графика лежат выше любой касательной к графику функции на этом интервале (рис.29).
Рис. 28
51
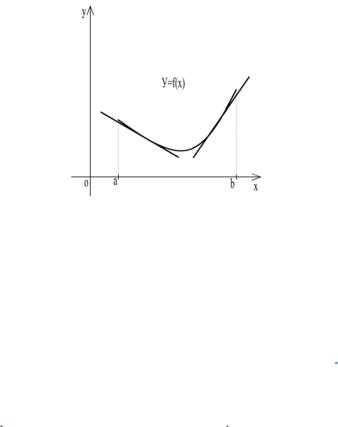
Рис. 29
Теорема. Достаточный признак выпуклости.
Если во всех точках интервала (a, b) вторая производная функцииf(x) отрицательна, т.е.f ''(x) < 0, то график функции на этом интервале выпуклый вверх. Если во всех точках интервала(a, b) вторая производная функцииf(x) положительна, т.е.
f ''(x)>0, то график функции на этом интервале выпуклый вниз.
Пример 6. Доказать, что график функцииy = x arctgx
везде выпуклый вниз.
Решение. Находим первую и вторую производные:
y' = (x arctgx)' = (x)' arсtgx + x(arсtgx)' = 1 arctg x + |
| x | ; | |||||
| 1 + x2 | |||||||
| x ′ | 1 |
| x'(1+ x2 )− x(1+ x2 )' |
|
|
| |
y" = arctgх+ |
| = |
| + |
| = |
| |
| 1+x2 | (1+ x2 )2 |
| |||||
| 1+x2 |
|
|
|
| |||
= |
| 1 | + | 1+x2 | −2x2 | = | 1+x2 | +1−x2 | = |
| 2 | > 0. | ||||
| + x2 |
| (1 | + x2)2 |
| (1 | + x2)2 |
| + x2)2 | |||||||
1 |
| (1 |
| |||||||||||||
Следовательно, по достаточному признаку график функции выпуклый вниз при x (−∞,+∞).
Определение. Точка, отделяющая выпуклую вверх часть графика непрерывной функции от выпуклой вниз, называется
точкой перегиба графика функции.
52

На рис. 30, 31, 32 точки О, А – точки перегиба.
Если в точке перегиба существует касательная к графику, то график функции с одной стороны от точки перегиба лежит над касательной, а с другой стороны – под касательной (рис. 30, 31).
Рис. 30
Теорема. Необходимый признак точки перегиба.
Если х0 – абсцисса точки перегиба графика функцииy = f(x), то вторая производнаяf "(x0) равна нулю или не существует.
Замечание 1. Таким образом, абсциссы точек перегиба графика функции следует искать среди точек, в которых вторая производная равна нулю или не существует.
Замечание 2. Равенствоf "(x0) = 0 является необходимым, но не достаточным признаком точки перегиба функции, имеющей вторую производную. Рассмотрим, например, функциюy = x4. Найдём производные:y' = 4x3, y " = 12x2 = 0 прих = 0.
Однако точка О (0; 0) не является точкой перегиба (рис. 33).
53

Рис. 31
Рис. 32
54

Рис. 33
Теорема. Достаточный признак точки перегиба.
Пусть функция y=f(x) непрерывна в точкех0, имеет вторую производную в некоторой окрестности точких0, за исключением, быть может, самой точких0. Если при переходе через точкух0 вторая производнаяf ''(х) меняет знак, то точка графика функцииМ (х0, f(x0)) – точка перегиба.
Доказательство. Так как вторая производнаяf ′′(x) слева и справа от точкиx0 имеет разные знаки, то направление выпуклости графика функции слева и справа от точкиx0 различны. Но тогда, по определению, точка графика функцииM (x0 ,f (x0 ))−
точка перегиба.
Пример 7. Найти точки перегиба и интервалы выпуклости вверх и вниз графика функцииy=x3-3x2-12x+3.
Решение. Находим производные: y=3x2-6x-12,y"=6x-6. Вторая производная обращается в нуль при x0=1. Так как f "(x)<0при x<1, то график функции выпуклый вверх на интервале
(-∞,1). Так какf "(х)> 0 прих>1, график функции выпуклый вниз на интервале (1,+∞). Следовательно,х0=1 – абсцисса точки перегиба. Найдем ординатуy0 =13-3 12-12 1+3=-11.Точка
M(1,-11) – точка перегиба графика функции.
55
studfiles.net
5.3. Исследование функций на выпуклость и вогнутость. Точки перегиба функций.
Функция  называется выпуклой (вогнутой) на интервале (a, b), если касательная расположена выше (ниже) графика функции.
называется выпуклой (вогнутой) на интервале (a, b), если касательная расположена выше (ниже) графика функции.
Теорема 1. Пусть  дважды дифференцируема на (a, b),
дважды дифференцируема на (a, b),  тогда
тогда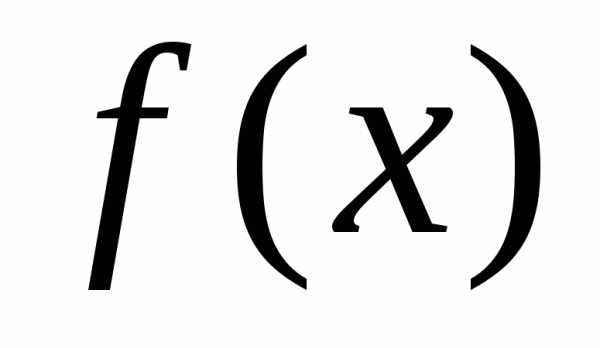 выпуклая (вогнутая) на (a, b).
выпуклая (вогнутая) на (a, b).
Точка называется точкой перегиба графика функции, если слева от этой точки график функции выпуклый (вогнутый), а справа – вогнутый (выпуклый).
Теорема 2 (необходимое условие перегиба). Пусть  - точка перегиба графика функции
- точка перегиба графика функции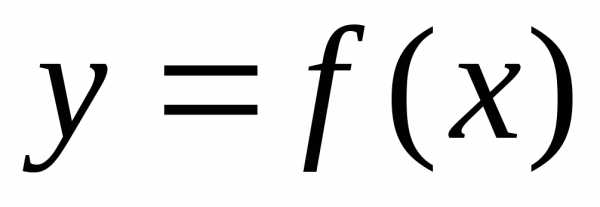 . Тогда илиили
. Тогда илиили не существует.
не существует.
Теорема 3 (достаточное условие перегиба). Пусть 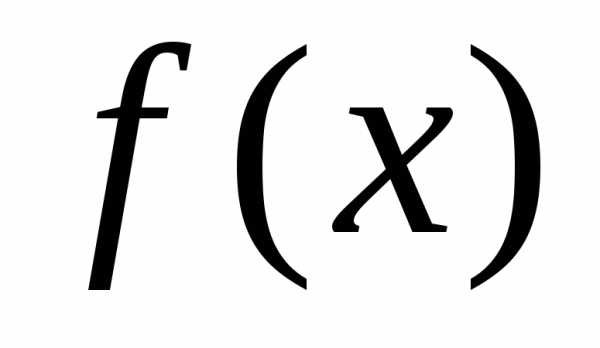 дважды дифференцируема в некоторой окрестности т.
дважды дифференцируема в некоторой окрестности т. и либо
и либо существует и конечна, либо
существует и конечна, либо не существует и
не существует и меняет знак при переходе через т.
меняет знак при переходе через т.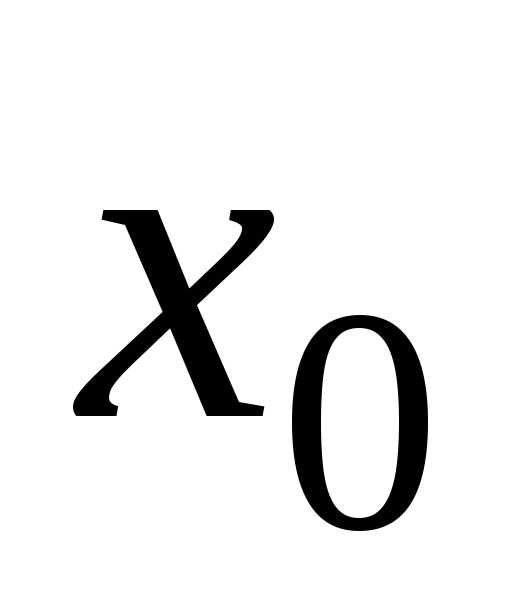 . Тогда
. Тогда
Пример. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции .
Область определения D(y)=R. Вычислим вторую производную.
.
.
Точки возможного перегиба :, т.к. и
и не существует и. Проверим смену знака
не существует и. Проверим смену знака :
:
- - + знак  .
.
-6 0
Следовательно, точка перегиба графика одна – (0,0). Функция выпукла на интервале  и вогнута на
и вогнута на .
.
Задачи для самостоятельного решения
22. Показать, что график функции везде выпуклый.
Найти точки перегиба и интервалы вогнутости и выпуклости для следующих функций.
24. . 25.26. .
.
27. . 28.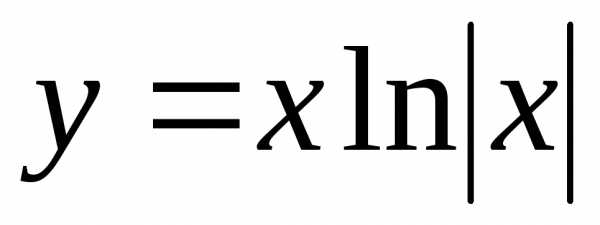 . 29..
. 29..
30. .
5.4. Асимптоты графика функции
Пусть существует такая прямая, что расстояние до нее от точки графика функции стремится к нулю при
стремится к нулю при стремящемся к бесконечности. Тогда прямая называетсяасимптотой графика функций. Прямая
стремящемся к бесконечности. Тогда прямая называетсяасимптотой графика функций. Прямая 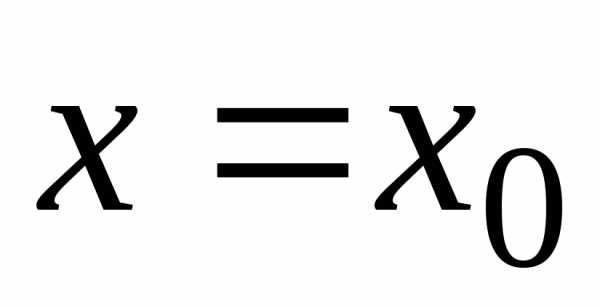 называетсявертикальной асимптотой, если хотя бы один из пределов:
называетсявертикальной асимптотой, если хотя бы один из пределов:  или
или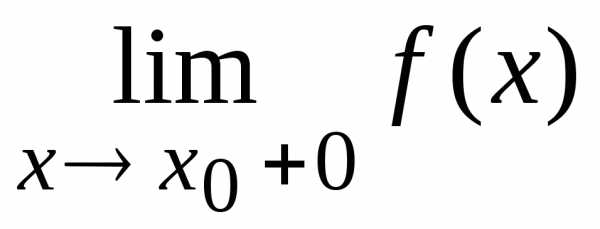
Если существуют конечные пределы  и, то прямаяестьнаклонная асимптота графика функции
и, то прямаяестьнаклонная асимптота графика функции  . Пределы могут не существовать или быть бесконечными прии существовать при(левая наклонная асимптота).
. Пределы могут не существовать или быть бесконечными прии существовать при(левая наклонная асимптота).
Если функция  может быть представлена в виде, где
может быть представлена в виде, где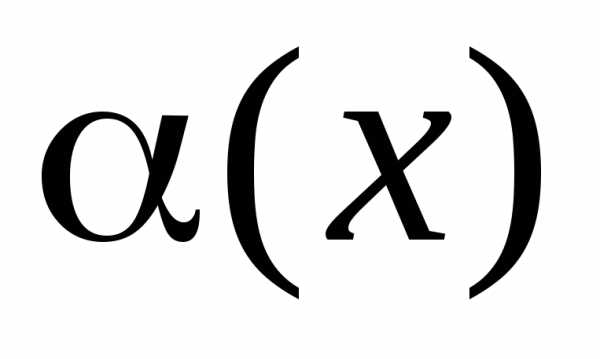 - бесконечно малая при, тоесть наклонная асимптота.
- бесконечно малая при, тоесть наклонная асимптота.
Пример. Найти асимптоты графика функции .
Найдем область определения функции: 
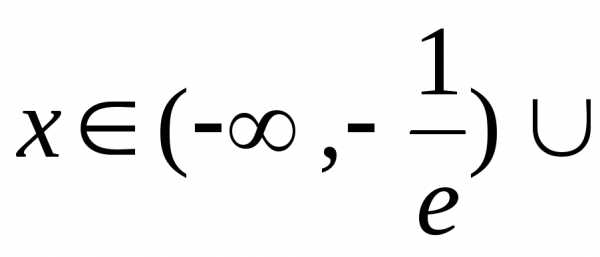
 ,
,
, ( применить правило Лопиталя)=. Следовательно- вертикальная асимптота, а
 , применим правило Лопиталя)=. Следовательно- наклонная асимптота.
, применим правило Лопиталя)=. Следовательно- наклонная асимптота.Задачи для самостоятельного решения
Найти асимптоты графиков следующих функций:
31.  . 32.
. 32. . 33.
. 33.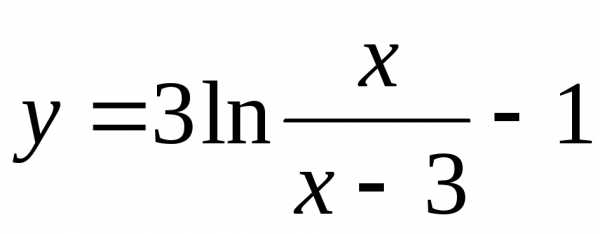 . 34.
. 34. .
.
35.  . 36.
. 36. . 37.. 38..
. 37.. 38..
5.5 Общая схема исследования функций.
Для построения графика функции  нужно провести исследование по следующей схеме:
нужно провести исследование по следующей схеме:
Область определения функции
 .
.Четность, нечетность, периодичность. Точки пересечения графика
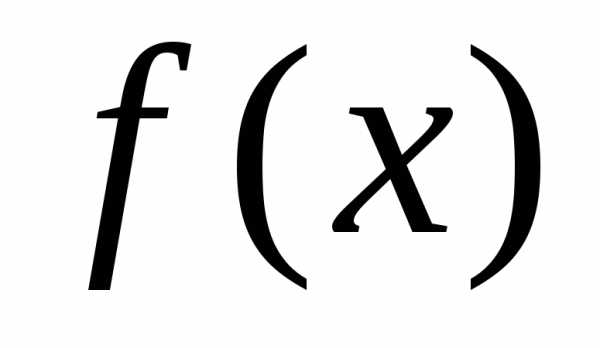 с осями координат.
с осями координат.Нахождение точек из области определения, в которых либо
 , либо
, либо не существует.
не существует.Нахождение точек из области определения, в которых либо
 , либо
, либо не существует.
не существует.Нахождение экстремумов, перегибов, интервалов возрастания и убывания, выпуклости и вогнутости графика по сводной таблице.
Асимптоты.
Построение графика.
Пример. Провести полное исследование функции и построить график.
В соответствие со схемой имеем:
.
Функция общего вида. График проходит через точку (0,0).
 . Точки возможного экстремума имеют абсциссы .
. Точки возможного экстремума имеют абсциссы . . Точка возможного перегиба имеет абсциссу x =0.
. Точка возможного перегиба имеет абсциссу x =0.Результаты сводим в таблицу
| x | | –3 | (–3, –1) | (–1, 0) | 0 |
|
| | + | 0 | – | + | 0 | + |
| | – |
| – | - | 0 | + |
| y |
| |
| | 0 | |
| лок. max | перегиб |
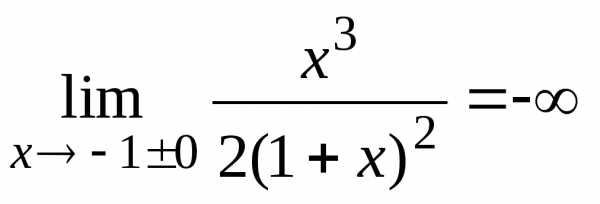
 . Следовательно
. Следовательно  - вертикальная асимптота. Выделим целую часть
- вертикальная асимптота. Выделим целую часть .и так как
.и так как - бесконечно малая при, то
- бесконечно малая при, то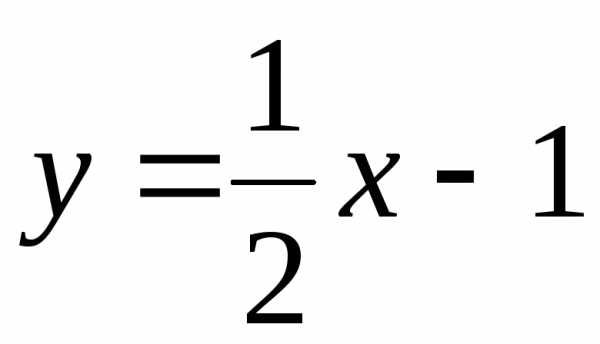 - наклонная асимптота.
- наклонная асимптота.Рисунок .
studfiles.net
3. Направление выпуклости функции. Точки перегиба
Пусть функция y=f(x) имеет конечную или бесконечную производную в каждой точке интервала Х = (а, b). Обозначим Г(Х) дугу графика функции f(x), соответствующую интервалу X.
Определение
Если дуга Г(Х) лежит не ниже (не выше) касательной к графику функции y=f(x), проведенной в любой точке M Г(Х), то функция или график функции называется выпуклым вниз (соответственно выпуклым вверх) в интервале X (рис. а).
Г(Х), то функция или график функции называется выпуклым вниз (соответственно выпуклым вверх) в интервале X (рис. а).
Точка на графике функции, в которой существует касательная к графику функции, называется точкой перегиба функции или графика функции, если она является границей дуг графика с разными направлениями выпуклости.
Рис. 9
Заметим, что в точке перегиба требуется существование касательной к графику.В некоторых учебных пособиях выпуклую вверх функцию называют выпуклой, а выпуклую вниз функцию вогнутой. Мы будем также пользоваться этими терминами, когда это удобно.
ТЕОРЕМА 4 (достаточное условие выпуклости вверх и вниз). Если функция f(x) дифференцируема дважды в интервале  и в ней f (x) > 0 (f (x) < 0), то f(x) является выпуклой вниз (соответственно выпуклой вверх) в интервале X.
и в ней f (x) > 0 (f (x) < 0), то f(x) является выпуклой вниз (соответственно выпуклой вверх) в интервале X.
Необходимое условие точки перегиба
Если M0 (x0, f(x0)) точка перегиба функции f(x), то либо и f (x0) = 0, либо f (x0) не существует (рис. б, в). Следовательно, абсциссы точек перегиба нужно искать в тех значениях x, при которых вторая производная либо равна нулю, либо не существует.
Первое достаточное условие точки перегиба
Пусть функция f(x) имеет производную (может быть бесконечную) в точке x0, существует вторая производная в проколотой окрестности точки x0 и либо f (x0) = 0, либо f (x0) не существует. Тогда если при переходе через x0 f (x) меняет знак, то (x0, f(x0)) является точкой перегиба.
Второе достаточное условие точки перегиба
Если ,, то точка точка перегиба функции.
точка перегиба функции.
Правило нахождения точек перегиба и промежутков выпуклости вверх и вниз:
1. Найти область определения функции f(x).
2. Найти f (x) и решить уравнение f (x) = 0 и найти точки x из области определения, в которых f (x) не существует.
3. Разбить область определения найденными в предыдущем пункте точками на промежутки и в них найти знаки второй производной.
4. Согласно теореме 4 в промежутках, где вторая производная положительна, функция выпукла вниз, а в промежутках, где вторая производная отрицательна, функция выпукла вверх.
5. В соответствии с необходимым условием абсциссы точек перегиба нужно искать среди значений, найденных в пункте 2. Пусть x0 такое значение. Если производная в точке x0 (конечная или бесконечная) существует и в интервалах непосредственно слева и справа от x0 вторая производная имеет разные знаки, то x0 абсцисса точки перегиба.
Типовые примеры
Исследовать функцию 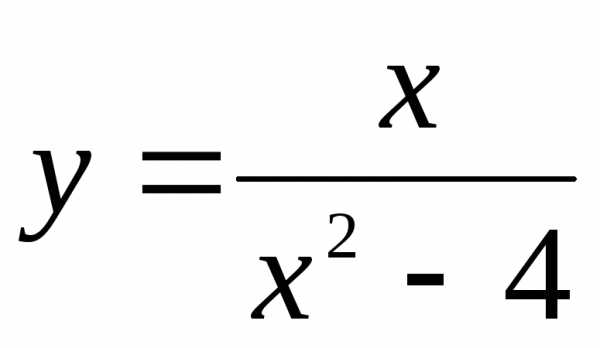 на выпуклость, вогнутость, найти точки перегиба.
на выпуклость, вогнутость, найти точки перегиба.
►1) Функция определена при всех действительных значениях x, таких, что x2-4 0, т.е. x 2.
2) Найдем вторую производную.

Рис. 10
y=0 при x = 0. y не существует при x = 2, но они не входят в область определения функции, поэтому они не могут быть абсциссами точек перегиба.
3) Разобьем область определения точкой x = 0 на интервалы (– ∞, -2),
(-2, 0), (0, 2), (2, +∞), в каждом из которых вторая производная сохраняет знак.
Определим знак второй производной в каждом из этих интервалов. В точке x=-3 из интервала (– ∞, -2) y< 0, следовательно, y< 0 во всем интервале (– ∞, -2). Аналогично определяем, что y > 0 в интервалах (-2, 0) и (2, +∞), y < 0 в интервале (0, 2) (рис. 5а).
4) Функция выпукла вверх в интервалах (– ∞, -2), (0, 2), выпукла вниз в интервалах (-2, 0), (2, +∞).
5) В интервалах (-2, 0), (0, 2) y имеет разные знаки. Значит, (0, 0) является точкой перегиба функции.
На рисунке б приведен схематически график функции. ◄
2. Исследовать функцию на экстремум, выпуклость. Найти точки перегиба.
►Данная функция определена и непрерывна на всей числовой оси. Найдем ее первую производную 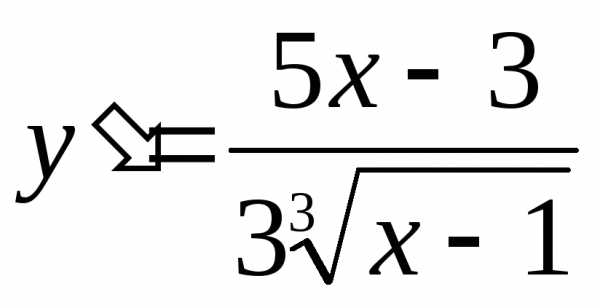 . Критическими точками являются
. Критическими точками являются  и
и Следовательно, интервалы возрастания и убывания таковы: . Сведем исследования в табл. ?.
Следовательно, интервалы возрастания и убывания таковы: . Сведем исследования в табл. ?.
Таблица ?
| Интервалы | | | | 1 | |
| f(x) | возрастает | | Убывает | 0 | возрастает |
| | >0 | 0 | <0 | | >0 |
| Выводы | max | min |
Найдем вторую производную
 . Очевидно, критические точки
. Очевидно, критические точки  и не существует). При переходе через точку
и не существует). При переходе через точку 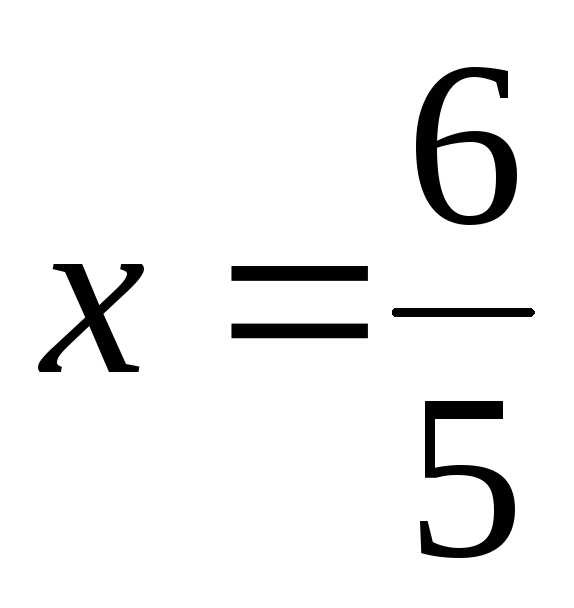
 меняет знак. Значит
меняет знак. Значит  – точка перегиба. При переходе через точку
– точка перегиба. При переходе через точку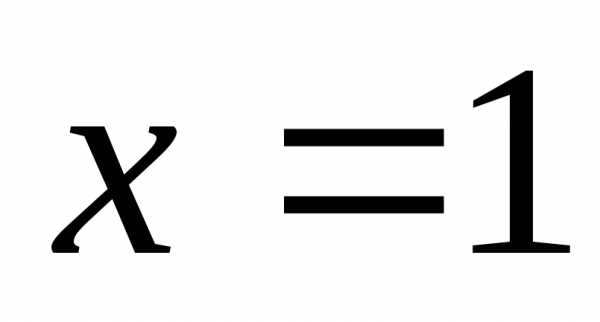 знака не меняет, следовательно, в этой точке перегиба нет.
знака не меняет, следовательно, в этой точке перегиба нет.Исследование удобно оформить в виде табл. ?.
Таблица ?
| Интервал | | 1 | | | |
| f(x) | выпукла вверх | выпукла вверх | выпукла вниз | ||
| | <0 | | <0 | 0 | >0 |
| Точка перегиба |
studfiles.net
Выпуклость и вогнутость графика функции. Точки перегиба (Лекция №10)
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
- Полуокружность выпукла на [–1; 1].
- Парабола y = x2 вогнута на интервале (-∞; +∞).
- График функции в одних интервалах может быть выпуклым, а в других вогнутым. Так график функции y = sin x на [0,2; π], выпуклый в интервале (0; π) и вогнутый в (π; 2π).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
Итак, уравнение кривой имеет вид y = f(x). Обозначим ординату касательной, соответствующую абсциссе x. Тогда . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет .
Разность f(x) – f(x0) преобразуем по теореме Лагранжа , где c между x и x0.
Таким образом,
.
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
- Предположим, что x>x0. Тогда x0<c1<c<x, следовательно, (x – x0) > 0 и (c – x0) > 0. Поэтому .
- Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
- Установить интервалы
выпуклости и вогнутости кривой y = 2 – x2.
Найдем y '' и определим, где вторая производная положительна и где отрицательна. y' = –2x, y'' = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
- y = ex. Так как y'' = ex > 0 при любых x, то кривая всюду вогнута.
- y = x3. Так как y'' = 6x, то y'' < 0 при x < 0 и y'' > 0 при x > 0. Следовательно, при x < 0 кривая выпукла, а при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.
Найдем производные заданной функции до второго порядка.
.
. Вторая производная не существует при x = 1. Исследуем эту точку на возможный перегиб.
Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
Возможные точки перегиба найдем, решив уравнение 2x2 – 1 = 0. Отсюда .
Точки перегиба . Функция выпукла на и вогнута на .
- y = ln (1 – x2). Область определения функции D(y) = (-1; 1).
.
при всех x из (–1; 1).
Следовательно, f(x) выпуклая на (–1; 1).
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е. или или . Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное, если прямая x = x0 является асимптотой, т. о. .
Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Примеры.
- Найти вертикальные асимптоты графика функции .
Так как , то прямая x = 2 является вертикальной асимптотой.
- .
Прямая x = 0 – вертикальная асимптота.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда . Аналогичное утверждение верно и при x → –∞.
Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что . Так как φ постоянный угол (φ ≠ π/2), то , но
MN = MK – NK = y - yас= f(x) - (kx+b).
Следовательно, мы можем записать следующее равенство .
Так как x → +∞, то должно выполняться равенство . Но при постоянных k и b и . Следовательно, , т.е. .
Если число k уже известно, то , поэтому .
Для доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство . Действительно
Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.
Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы
.
Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
- .
- Вертикальные:
x = 0 – вертикальная асимптота.
- Наклонные:
.
При x → - ∞ получим те же значения k и b. Следовательно, прямая y = x + 2 является наклонной асимптотой.
- Вертикальные:
- y = e–x sin x + x.
- Функция определена и непрерывна на всей числовой прямой, следовательно, вертикальных асимптот нет.
-
а) .
Итак, при x → +∞ наклонная асимптота у= х.
б) , т. к.
, поэтому при x → - ∞ наклонных асимптот нет.
- y = x – 2arctg x.
- Вертикальных асимптот нет.
-
а) .
. Наклонная асимптота y = x – π при .
б) при .
www.toehelp.ru
7.4. Выпуклость, вогнутость графика функции, точки перегиба
Пусть  – функция, дифференцируемая на интервале
– функция, дифференцируемая на интервале  . Рассмотрим кривую, являющуюся графиком функции
. Рассмотрим кривую, являющуюся графиком функции 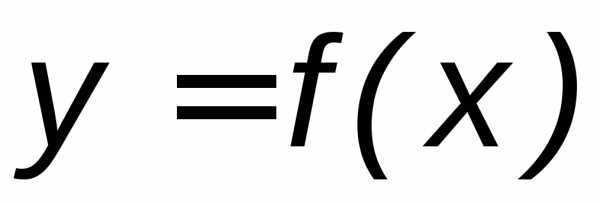 .
.
Кривая, заданная функцией  , называется выпуклой на интервале
, называется выпуклой на интервале  , если все точки кривой лежат ниже любой ее касательной на этом интервале.
, если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая называется вогнутой на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале.
Точка кривой M0(x0, f(x0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Теорема 4 (достаточные условия выпуклости и вогнутости графика функции). Если во всех точках интервала  вторая производная функции
вторая производная функции  отрицательна, т. е. , то кривая
отрицательна, т. е. , то кривая  на этом интервале выпукла; если во всех точках интервала
на этом интервале выпукла; если во всех точках интервала  –, то кривая
–, то кривая 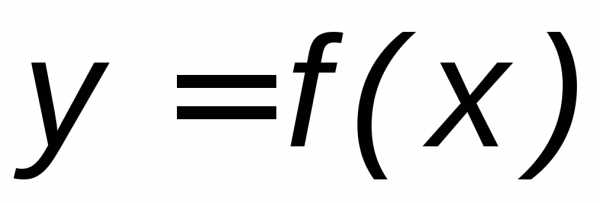 на этом интервале вогнута.
на этом интервале вогнута.
Пример 7.8. Определить направление выпуклости и точки перегиба кривой
Решение.
Ищем точки х из области определения функции, в которых  или не существует.
или не существует.
Вторая производная равна нулю 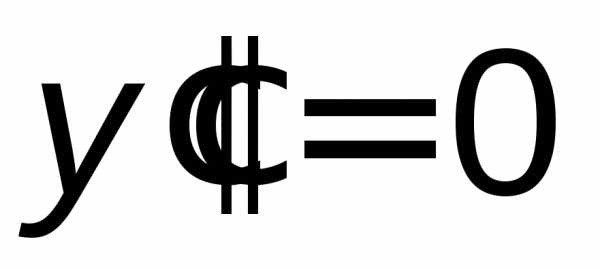 в точках . Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точекх, которые могли бы быть абсциссами точек перегиба, нет, так как
в точках . Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точекх, которые могли бы быть абсциссами точек перегиба, нет, так как  существует всюду.
существует всюду.
Исследуем найденные точки, определяя знак  слева и справа от каждой из них. Результаты исследования запишем в таблицу, подобную той, которая составляется при отыскании точек экстремума (табл. 3).
слева и справа от каждой из них. Результаты исследования запишем в таблицу, подобную той, которая составляется при отыскании точек экстремума (табл. 3).
Таблица 3
| x |
| 0 | (0, 1) | 1 |
|
|
| 0 | 0 |
| ||
|
| выпукла | нет перегиба | выпукла | точка перегиба | вогнута |
Выполним построение (рис. 6).

Рис. 6
7.5. Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Если , то прямая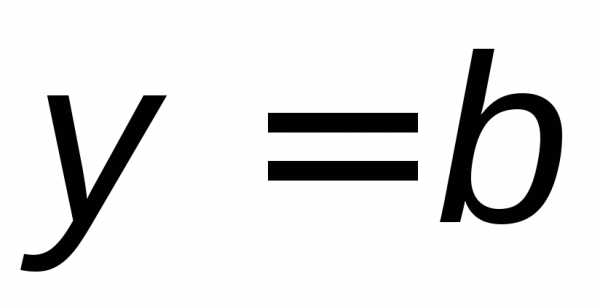 является асимптотой графика
является асимптотой графика  (при ). Эта асимптота параллельна осиOx и называется горизонтальной асимптотой (рис. 7). Аналогично, прямая
(при ). Эта асимптота параллельна осиOx и называется горизонтальной асимптотой (рис. 7). Аналогично, прямая 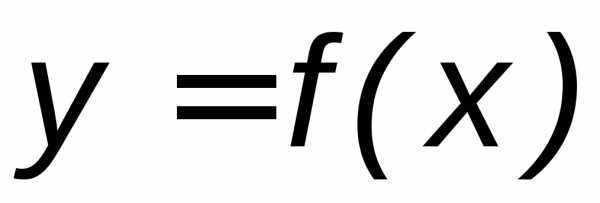 является асимптотой графика y = f(x) (при ), если.
является асимптотой графика y = f(x) (при ), если.
Рассмотрим асимптоты, параллельные оси Oy.
Прямая x=x0 называется вертикальной асимптотой, если хотя бы один из пределов  ,
, , является бесконечным (рис. 8).
, является бесконечным (рис. 8).
Рис. 8
Следовательно, для отыскания вертикальных асимптот нужно найти точки разрыва функции второго рода.
Пример 7.9. Найти вертикальные асимптоты для функции  .
.
Решение.
Функция 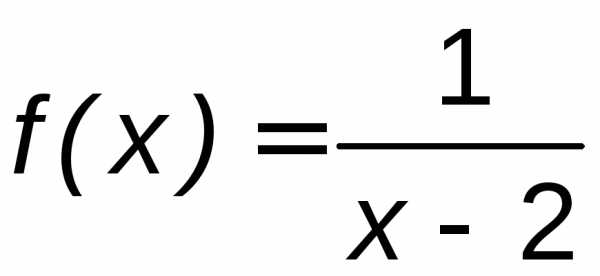 определена и непрерывна во всех точках числовой оси, за исключением точкиx0 = 2, в которой функция терпит разрыв,
определена и непрерывна во всех точках числовой оси, за исключением точкиx0 = 2, в которой функция терпит разрыв,
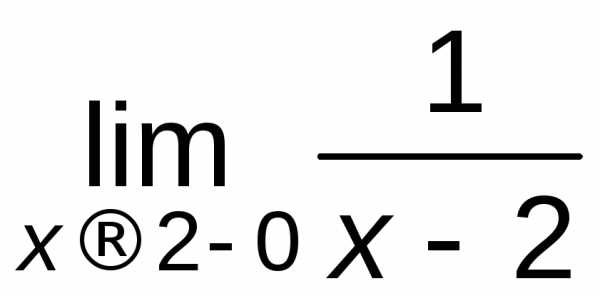 = –,
= –, = +. Следовательно, прямая х=2 является вертикальной асимптотой для графика y =
= +. Следовательно, прямая х=2 является вертикальной асимптотой для графика y = . Кроме того,
. Кроме того, = 0 и
= 0 и  = 0, следовательно, прямаяy = 0 является горизонтальной асимптотой при и при.
= 0, следовательно, прямаяy = 0 является горизонтальной асимптотой при и при.
Рассмотрим асимптоты, которые не параллельны координатным осям (рис. 9). Будем называть их наклонными асимптотами.
Прямая называется наклонной асимптотой функции  , если функцию можно представить в виде
, если функцию можно представить в виде
, (7.1)
где , при.
Определим числа k и b.
Поделим обе части равенства (7.1) на  и перейдем к пределу при:
и перейдем к пределу при:
Откуда:
 (7.2)
(7.2)
Определим коэффициент  .
.
Равенство (7.1) перепишем в виде:
Перейдем к пределу , получим.
.
(7.3)
Если хотя бы один из пределов (7.2), (7.3) не существует, то при кривая не имеет наклонной асимптоты.
Аналогично решается вопрос об асимптотах при .
Замечание. Отдельно находить горизонтальные асимптоты нет необходимости: они будут найдены при нахождении наклонных асимптот (при k=0).
Пример 7.10. Найти асимптоты линии .
Решение.
Функция определена, непрерывна на бесконечном интервале поэтому вертикальных асимптот нет.
поэтому вертикальных асимптот нет.
Найдем наклонные асимптоты. Для этого вычислим пределы (7.1), (7.3) при и при:
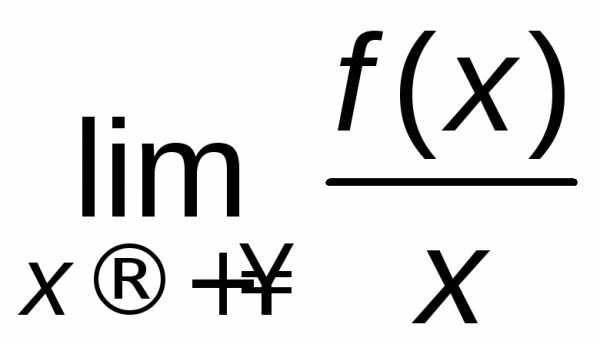 =
= 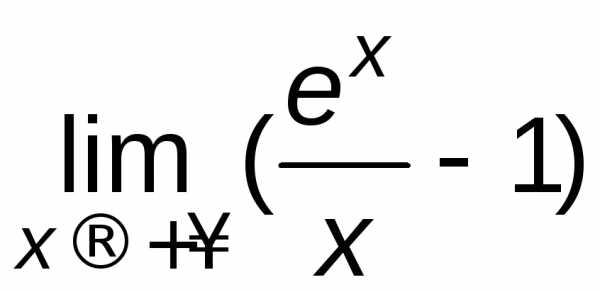 =
= ,
,
так как  (проверьте это по правилу Лопиталя). Отсюда следует, что принаклонных асимптот нет.
(проверьте это по правилу Лопиталя). Отсюда следует, что принаклонных асимптот нет.
 =
= 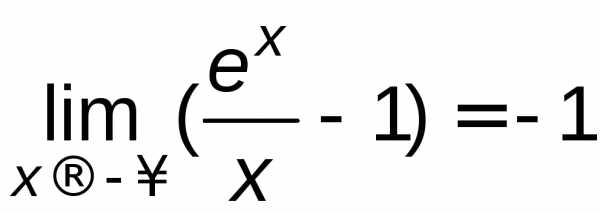 , так как
, так как ,
,
отсюда 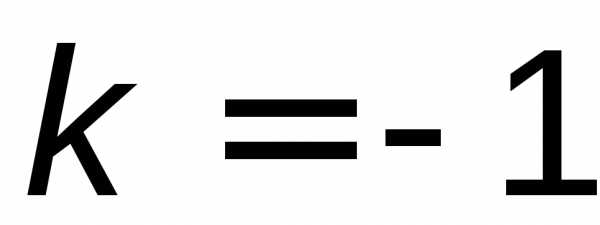 . Далее,значит,b = 0.
. Далее,значит,b = 0.
Итак, прямая y=-x есть наклонная асимптота при для графика функции(рис. 10).

studfiles.net
18
18. Выпуклые функции. Признаки выпуклости функции. Необходимый признак точки перегиба, достаточный признак точки перегиба, их геометрический признак. Примеры
Выпуклые функции
Функция f на интервале
1) выпукла (выпукла вниз), если
2) строго выпукла (строго выпукла вниз), если
3) выпукла вверх, если
4) строго выпукла вверх, если
Признаки выпуклости дифференцируемых функций
1. Если f' возрастает на , тоf выпукла на (еслиf' строго возрастает, то f строго выпукла).
2. Если , тоf выпукла на (еслиобращаясь в нуль, возможно, лишь в конечном числе точек, тоf строго выпукла).
3. Функция f выпукла тогда и только тогда, когда график функции лежит не ниже касательной, проведенной к нему в любой его точке.
Свойства выпуклых функций
В частности:
2.
3. Точки любой дуги графика лежат под хордой, стягивающей эту дугу.
4. Функция f непрерывна на интервале и имеет в каждой его точке конечные односторонние производные.
5. Функция f имеет на не более одного локального минимума и не имеет локальных максимумов.
Точки перегиба
Пусть функция f определена в некоторой окрестности точки x0, непрерывна в точке x0 и имеет в этой точке конечную или бесконечную производную. Если при переходе через точку x0 функция f меняет направление выпуклости, то x0 называют точкой перегиба функции f, а точку (x0; f(x0)) - точкой перегиба графика функции f. График функции переходит с одной стороны касательной, проведенной в точке (x0; f(x0)), на другую сторону. Точки перегиба f - точки экстремума для f'.
Необходимое условие перегиба.
Сформулируем необходимое условие перегиба графика функции.
Пусть график функции y=f(x) имеет перегиб в точке и имеет принепрерывную вторую производную, тогда выполняется равенство.
Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения , в которых вторая производная равна нулю, являются абсциссами точек перегиба.
Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все из области определения функции, для которыхи. Обычно это точки, в которых знаменатель первой производной обращается в ноль.
Первое достаточное условие перегиба.
После того как найдены все , которые могут быть абсциссами точек перегиба, следует воспользоватьсяпервым достаточным условием перегиба графика функции.
Пусть функция y=f(x) непрерывна в точке , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки. Тогда, если в пределах этой окрестности слева и справа от, вторая производная имеет разные знаки, тоявляется точкой перегиба графика функции.
Как видите первое достаточное условие не требует существования второй производной в самой точке , но требует ее существование в окрестности точки.
Сейчас обобщим всю информацию в виде алгоритма.
Алгоритм нахождения точек перегиба функции.
Находим все абсциссы возможных точек перегиба графика функции (илии) и выясняем, проходя через какиевторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точкибудут точками перегиба графика функции.
Второе достаточное условие перегиба.
Если , а , тогда является абсциссой точки перегиба графика функцииy=f(x).
Пример.
Выяснить, является ли точка точкой перегиба графика функции .
Решение.
Для начала убедимся, что точка принадлежит графику функции:
Функция определена для всех действительных значений аргумента. Найдем первую и вторую производные.
Вторая производная обращается в ноль при x=3, то есть необходимое условие перегиба графика функции в точке выполнено, и эта точка может быть точкой перегиба. Воспользуемся вторым достаточным условием перегиба. Для этого найдем третью производную и убедимся, что ее значение при x=3 отлично от нуля.
Очевидно, что значение третьей производной отлично от нуля для любых x, в том числе и для x=3. Поэтому, по второму достаточному условию перегиба графика функции, точка является точкой перегиба.
studfiles.net