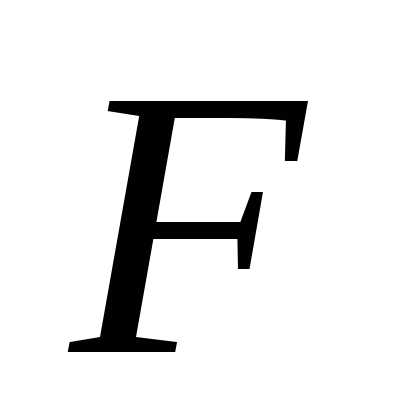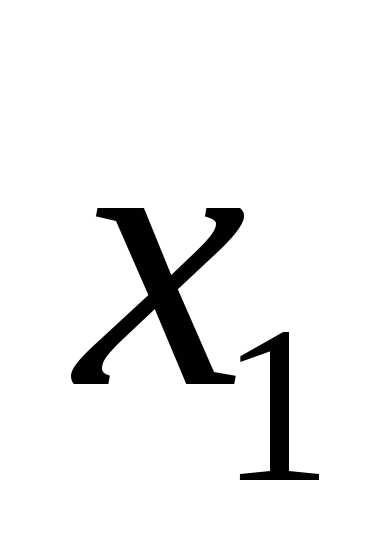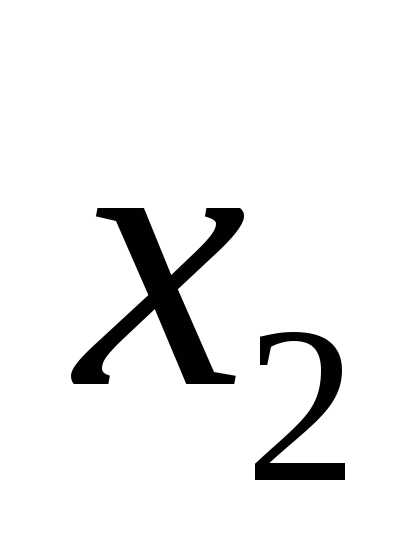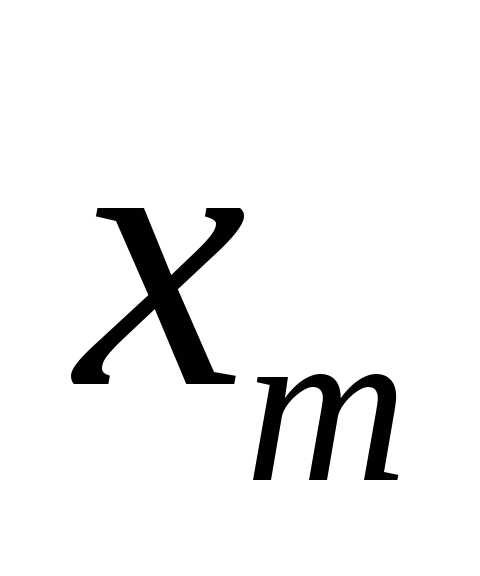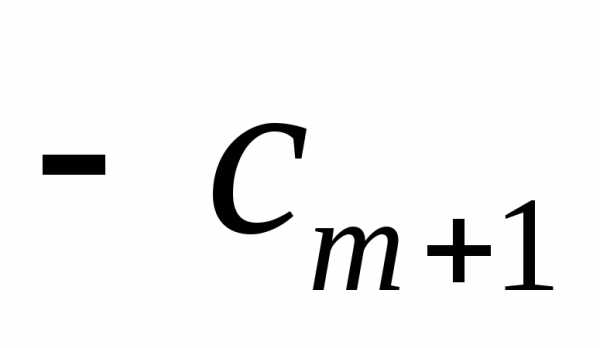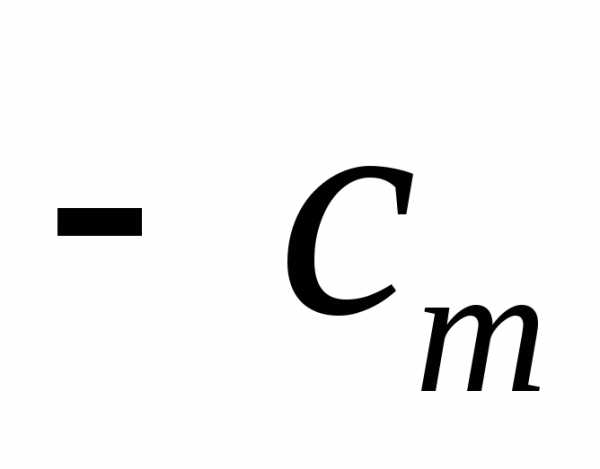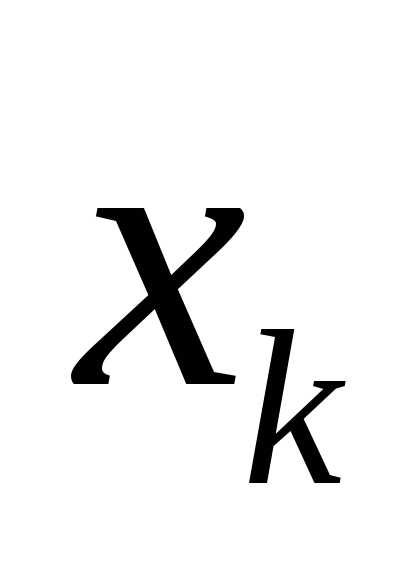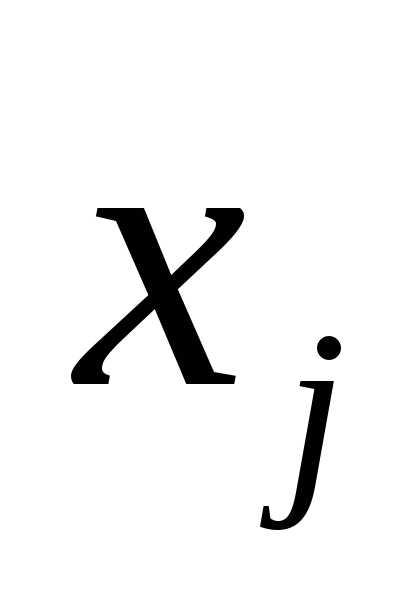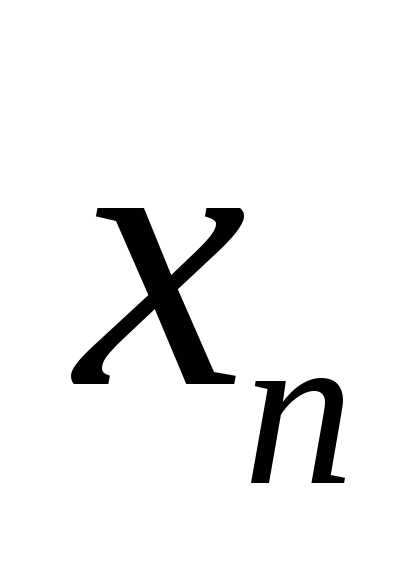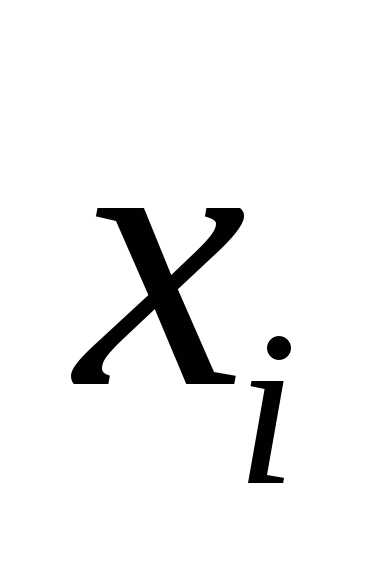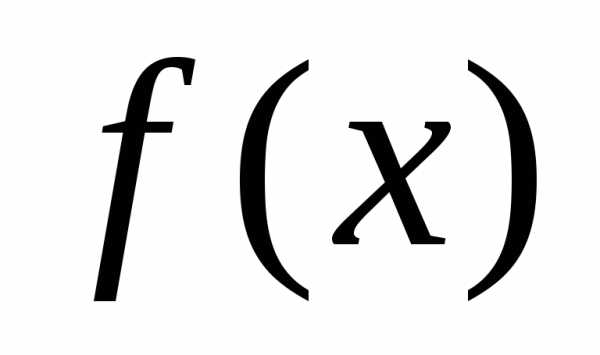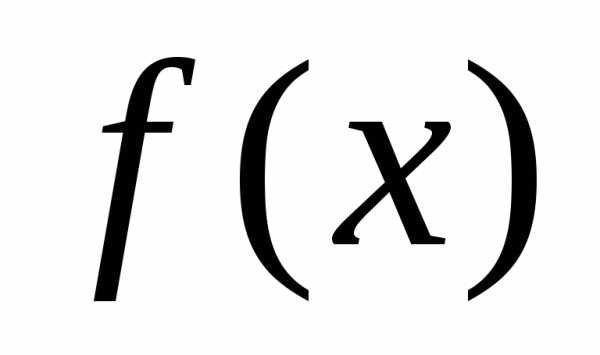Симплекс метод решения задач линейного программирования: типичный пример и алгоритм. Алгоритм симплекс метода
Решение симплекс методом задачи ЛП: пример и алгоритм
Симплекс метод - это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).
Симплекс метод был предложен американским математиком Р.Данцигом в 1947 году, с тех пор для нужд промышленности этим методом нередко решаются задачи линейного программирования с тысячами переменных и ограничений.
Перед тем, как перейти к алгоритму симплекс метода, несколько определений.
Всякое неотрицательное решение системы ограничений называется допустимым решением.
Пусть имеется система m ограничений с n переменными (m n).
Допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных и n - m неосновных. (небазисных, или свободных) переменных. Неосновные переменные в базисном решении равны нулю, основные же переменные, как правило, отличны от нуля, то есть являются положительными числами.
Любые m переменных системы m линейных уравнений с n переменными называются основными, если определитель из коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (или свободными).
Алгоритм симплекс метода
- Шаг 1. Привести задачу линейного программирования к канонической форме. Для этого перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножить на - 1) и в каждое ограничение ввести дополнительные переменные (со знаком "плюс", если в исходном неравенстве знак "меньше или равно", и со знаком "минус", если "больше или равно").
- Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению.
- Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению.
- Шаг 4. Из неосновных переменных, входящих в линейную форму с отрицательными (положительными) коэффициентами, выбирают ту, которой соответствует наибольший (по модулю) коэффициент, и переводят её в основные. Переход к шагу 2.
Важные условия
- Если допустимое базисное решение даёт оптимум линейной формы (критерий оптимальности выполнен), а в выражении линейной формы через неосновные переменные отсутствует хотя бы одна из них, то полученное оптимальное решение - не единственное.
- Если в выражении линейной формы имеется неосновная переменная с отрицательным коэффициентом в случае её максимизации (с положительным - в случае минимизации), а во все уравнения системы ограничений этого шага указанная переменная входит также с отрицательными коэффициентами или отсутствует, то линейная форма не ограничена при данной системе ограничений. В этом случае её максимальное (минимальное) значение записывают в виде .
Путём построения симплексных таблиц решить задачу линейного программирования намного проще, чем путём алгебраических преобразований, который показан в следующем параграфе. Симплексные таблицы очень наглядны. Существует несколько разновидностей правил работы с симплексными таблицами. Мы разберём правило, которое чаще всего называется правилом ведущего столбца и ведущей строки.
Будет нелишним открыть в новом окне пособие Действия с дробями: их, дробей в задачах на симплекс-метод, мягко говоря, хватает.
Пример. Найти максимум функции при ограничениях
Решение.
Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Это было сделано с соблюдением следующего правила: если в первоначальном ограничении знак "меньше или равно", то добавочную переменную нужно прибавлять, а если "больше или равно", то добавочную переменную нужно отнимать.
Введённые добавочные переменные принимаем за основные (базисные). Тогда и - неосновные (свободные) переменные.
Выразив основные (базисные) переменные через неосновные (свободные), получим
Функцию цели также выразим через неосновные (свободные) переменные:
Из коэффициентов при переменных (неизвестных) построим первую симплексную таблицу.
| Таблица 1 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X2 | |||
| X3 | -2 | 1 | -2 | |
| X4 | -4 | -1 | -1 | |
| X5 | 2 | 1 | -1 | |
| X6 | 6 | 0 | 1 | |
| F | 0 | -1 | -2 | |
Последнюю строку таблицы, в которой записаны функция цели и коэффициенты при свободных переменных в ней, будем называть в индексной строкой.
Полученное решение не оптимально, так как в индексной строке коэффициенты при свободных переменных отрицательны. То есть оптимальным будет то решение, в котором коэффициенты при свободных переменных в индексной строке будут больше или равны нулю.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей таблице найдём наибольшее (по модулю) из чисел и . Это число 2. Поэтому ведущий столбец - тот столбец, в котором записано
Для определения ведущей строки находим минимум отношений свободных членов к элементам ведущего столбца, причём если в числителе положительное число, а в знаменателе отрицательное, отношение считается равным бесконечности.
Итак,
.
Поэтому ведущая строка - та, в которой записано
Ведущим элементом, таким образом, является -2.
Составляем вторую симплексную таблицу.
Новый базисный элемент вписываем первой строкой, а столбец, в котором стояло , вписываем новую свободную переменную
Заполняем первую строку. Для этого все числа, стоящие в ведущей строке таблицы 1, делим на ведущий элемент и записываем в соответствующий столбец первой строки таблицы 2, кроме числа, стоящего в ведущем столбце, куда записывается величина, обратная ведущему элементу (то есть, единица, делённая на ведущий элемент).
Заполняем столбец вспомогательных коэффициентов. Для этого числа ведущего столбца таблицы 1, кроме ведущего элемента, записываем с противоположными знаками в графу вспомогательных коэффициентов таблицы 2.
| Таблица 2 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X3 | |||
| X2 | 1 | -1/2 | -1/2 | |
| X4 | -3 | -3/2 | -1/2 | 1 |
| X5 | 3 | 1/2 | -1/2 | 1 |
| X6 | 5 | 1/2 | 1/2 | -1 |
| F | 2 | -2 | -1 | 2 |
Кто ещё не открыл в новом окне пособие Действия с дробями, может сделать это сейчас, поскольку самое время.
Для получения остальных строк таблицы 2 числа, уже стоящие в первой строке этой таблицы, умножаем на вспомогательный коэффициент, стоящий в заполняемой строке, и к результату прибавляем число из таблицы 1, стоящее в той же строке при соответствующей переменной.
Например, для получения свободного члена второй строки число 1 умножаем на 1 и прибавляем из таблицы 1 число -4. Получаем -3. Коэффициент при во второй строке находим так же: . Так как в предыдущей таблице отсутствует столбец с новой свободной переменной , то коэффициент второй строки в столбце новой свободной переменной будет (то есть из таблицы 1 прибавляем 0, так как в таблице 1 столбец с отсутствует).
Так же заполняется и индексная строка:
Полученное таким образом решение вновь не оптимально, так как в индексной строке коэффициенты при свободных переменных вновь отрицательны.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей симплексной таблице найдём наибольшее (по модулю) из чисел и , то есть, модулей коэффициентов в индексной строке. Это число 2. Поэтому ведущий столбец - тот столбец, в котором записано .
Для поиска ведущей строки найдём минимум отношений свободных членов к элементам ведущей строки. Получаем:
.
Следовательно, ведущая строка - та, в которой записано , а ведущим элементом является -3/2.
Составляем третью симплексную таблицу
Новую базисную переменную записываем первой строкой. В столбец, в котором было , вписываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
| Таблица 3 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X4 | X3 | |||
| X1 | 2 | -2/3 | 1/3 | |
| X2 | 2 | -1/3 | -1/3 | 1/2 |
| X5 | 2 | 1/3 | -2/3 | |
| X6 | 4 | 1/3 | 1/3 | -1/2 |
| F | 6 | -4/3 | -1/3 | 2 |
Вычисление остальных строк на примере второй строки:
Полученное решение вновь не оптимальное, поскольку коэффициенты при свободных неизвестных в индексной строке вновь отрицательные.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к четвёртой симплексной таблице найдём наибольшее из чисел и . Это число .
Следовательно, ведущий столбец - тот, в котором записано .
Для нахождения ведущей строки найдём минимум модулей отношений свободных членов к элементам ведущего столбца:
.
Поэтому ведущая строка - та, в которой записано , а ведущий элемент 1/3.
В четвёртой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X3 | |||
| X4 | 6 | 3 | -2 | |
| X1 | 6 | 2 | -1 | 2/3 |
| X2 | 4 | 1 | -1 | 1/3 |
| X6 | 2 | -1 | 1 | -1/3 |
| F | 14 | 4 | -3 | 4/3 |
Вычисление остальных строк на примере второй строки:
Полученное решение так же не оптимально, но оно уже лучше предыдущих, так как один из коэффициентов при свободных переменных в индексной строке неотрицателено.
Для улучшения плана перейдём к следующей симплексной таблице.
Найдём наибольшее из чисел 4 и . Это число 4. Следовательно, ведущий столбец .
Для нахождения ведущей строки найдём
.
Следовательно, ведущая строка - та, в которой записано . Но и уже были вместе среди свободных переменных. Поэтому для перевода очередной переменной из свободных в базисные выбираем другой ведущий столбец - тот, в котором записано .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для нахождения ведущей строки найдём
.
Следовательно, ключевая строка - та, в которой записано , а ведущий элемент 1.
В пятой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X6 | |||
| X3 | 2 | -1 | 1 | |
| X4 | 10 | 2 | ||
| X1 | 8 | 1 | ||
| X2 | 6 | 1 | ||
| F | 20 | 1 | 3 | 3 |
Попробуем сразу узнать, не является ли решение оптимальным. Поэтому для остальных строк вычислим только свободные члены (чтобы узнать значения базисных переменных при равенстве свободных переменных нулю) и коэффициенты при свободных переменных в индексной строке.
Свободные члены:
- во второй строке ;
- в третьей строке ;
- в четвёртой строке .
Индексная строка:
Смотрим в симплексную таблицу 5. Видим, что получено оптимальное решение, так как коэффициенты при свободных неизвестных в индексной строке неотрицательны.
Ответ:
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс методом.
Решим алгебраическими преобразованиями тот же пример, что и в предыдущем параграфе. Следует отметить, что при решении этой разновидностью симплекс метода лучше не записывать функцию цели в виде , так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий оптимальности, будет модифицирован следующим образом.
Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, перейти к новому базисному решению.
Пример. Найти максимум функции при ограничениях
Решение.
Шаг I. Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Введённые добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда и - неосновные переменные.
Выразив основные переменные через неосновные, получим
Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение , которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдём к улучшенному.
Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести и , так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, а это произойдёт, если переведём любую из них в основные переменные, переменная увеличится).
Попробуем перевести в основные переменную . Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при . Имеем . Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную , которая в исходном базисном решении положительна. Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдёт.
Если же перевести в основные переменную , то наименьшее отношение свободных членов к коэффициентам при составит . Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя в основные, а в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим в основные, а в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось первое уравнение.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг II.
Основные переменные , неосновные переменные .
Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим
Следовательно, имеем новое базисное решение , которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и предвидели, только одна переменная отрицательна (а именно ).
От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно показывает, что в основные переменные можно перевести и . Переведём в основные переменные . Найдём наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при . Имеем . Значит, в неосновные переменные нужно перенести . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.
В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции - бесконечность и когда система не имеет ни одного решения.
Шаг III.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Новое базисное решение имеет вид . Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Так как мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.
Переводим в число основных переменную , имеющую больший положительный коэффициент. Находим . Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем. Оно показывает, что при переменная и поэтому перейдёт в число неосновных.
В некотором особом случае решение завершается на III шаге: это случай, когда оптимальное решение - не единственное.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг IV.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через те же неосновные переменные, примет вид . Продолжим перебор для поиска максимума.
Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная является основной. Находим . Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что при переменная и переходит в число неосновных.
Шаг V.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение является оптимальным, а максимум линейной формы
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Начало темы "Линейное программирование"
Продолжение темы "Линейное программирование"
Поделиться с друзьями
function-x.ru
Алгоритм и пример симплекс-метода (ММЭ). Пример решения симплекс-методом
Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.3
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
18 | 1 | 3 | ||
16 | 2 | 1 | ||
5 | 0 | 1 | ||
21 | 3 | 0 | ||
0 | –2 | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности.
Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.
Таблица 5.4
Исходная симплекс-таблица
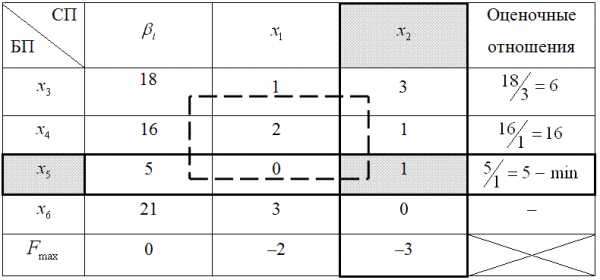
В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.
Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».
9 этап: преобразование симплекс-таблицы.
Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.
9.1. Преобразование разрешающего элемента.
Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:
Полученный результат вписываем в аналогичную клетку таблицы 5.5.
9.2. Преобразование разрешающей строки.
Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.
9.3. Преобразование разрешающей колонки.
Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.
9.4. Преобразование остальных элементов симплекс-таблицы.
Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».
К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5.4), а в числителе произведение двух других неиспользованных вершин, т.е.:
«х3»: .
Аналогично преобразуются значения других клеток:
«х3 х1»: ;
«х4»: ;
«х4 х1»: ;
«х6»: ;
«х6 х1»: ;
«»: ;
«х1»: .
В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).
II итерация:
1 этап: составление симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.5
Симплекс-таблица II итерации
СП БП | Оценочные отношения | |||
–(3/1)=–3 | ||||
–(1/1)=–1 | ||||
5/1=5 | 0/1=0 | (1)–1=1 | ||
–(0/1)=0 | ||||
–(–3/1)=3 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):
.
Как видно, при данном базисном решении значение целевой функции =15, что больше чем при предыдущем базисном решении.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.5, такой колонкой является только одна колонка: «х1». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Согласно полученным значениям положительных оценочных отношений в таблице 5.6, минимальным является отношение, соответствующее строке «х3». Следовательно, ее принимаем в качестве разрешенной.
Таблица 5.6
Симплекс-таблица II итерации
СП БП | Оценочные отношения | |||
3 | 1 | –3 | 3/1=3 – min | |
11 | 2 | –1 | 11/2=5,5 | |
5 | 0 | 1 | – | |
21 | 3 | 0 | 21/3=7 | |
15 | –2 | 3 |
9 этап: преобразование симплекс-таблицы.
Преобразования симплекс-таблицы (таблицы 5.6) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.7.
III итерация
1 этап: построение новой симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.7
Симплекс-таблица III итерации
СП БП | Оценочные отношения | |||
3/1=3 | (1)–1=1 | –3/1=–3 | ||
–(2/1)=–2 | ||||
–(0/1)=0 | ||||
–(3/1)=–3 | ||||
–(–2/1)=2 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.7):
.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.7 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.7 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.7) содержится отрицательный элемент: –3 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.7, такой колонкой является только одна колонка: «х5». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Согласно полученным значениям положительных оценочных отношений в таблице 5.8, минимальным является отношение, соответствующее строке «х4». Следовательно, ее принимаем в качестве разрешенной.
Таблица 5.8
Симплекс-таблица III итерации
СП БП | Оценочные отношения | |||
3 | 1 | –3 | – | |
5 | –2 | 5 | 5/5=1 – min | |
5 | 0 | 1 | 5/1=5 | |
12 | –3 | 9 | 12/9=1? | |
21 | 2 | –3 |
9 этап: преобразование симплекс-таблицы.
Преобразования симплекс-таблицы (таблицы 5.8) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.9.
IV итерация
1 этап: построение новой симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.9
Симплекс-таблица IV итерации
СП БП | Оценочные отношения | |||
–(–3/5)=3/5 | ||||
5/5=1 | –2/5 | (5)–1= | ||
–(1/5)=–1/5 | ||||
–(9/5)=–9/5 | ||||
–(–3/5)=3/5 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:
.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
7 этап: проверка альтернативности решения.
Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
Ответ: оптимальное значение целевой функции рассматриваемой задачи =24, которое достигается при .
Пример 5.2. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.10
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
18 | 1 | 3 | ||
16 | 2 | 1 | ||
5 | 0 | 1 | ||
21 | 3 | 0 | ||
0 | –2 | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
7 этап: проверка альтернативности решения.
Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
Ответ: оптимальное значение целевой функции рассматриваемой задачи =0, которое достигается при .
Пример 5.3. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация
1 этап: составление исходной симплекс-таблицы.
Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х1 и х2.
Умножим (поэлементно) первую строку на –3 и сложим со второй:
.
Умножим вторую строку на :
.
Сложим вторую с первой строкой:
.
В результате система ограничений примет следующий вид:
Выразим базисные переменные через свободные:
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:
.
Запишем целевую функцию в следующем виде:
.
Составим исходную симплекс-таблицу:
Таблица 5.11
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
–1 | 0 | |||
0 | 2 | |||
4 | – | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х2, равная нулю.
3 этап: проверка совместности системы ограничений ЗЛП.
Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.
Еще записи по теме
www.ikasteko.ru
Алгоритм симплекс-метода.
Изложим теперь этот метод решения, в общем виде.
Пусть дана симплексная форма задачи ЛП, то есть каноническая задача ЛП, матрица системы которой имеет разрешенный вид, свободные члены неотрицательны и целевая функция зависит только от свободных переменных:
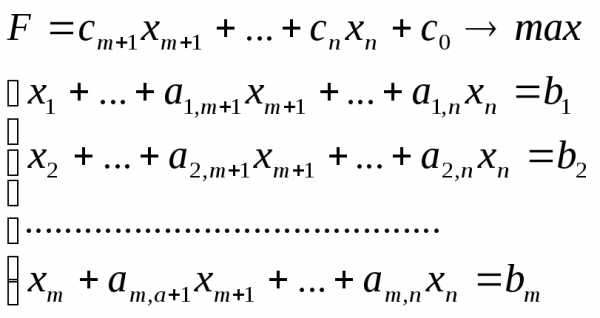(1)
Здесь мы считаем свободными переменные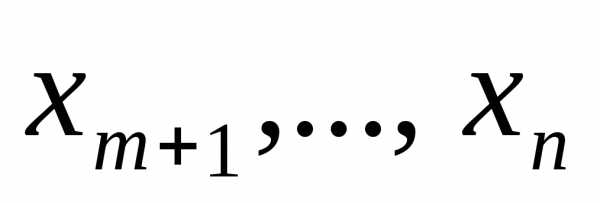 
. Запишем функцию
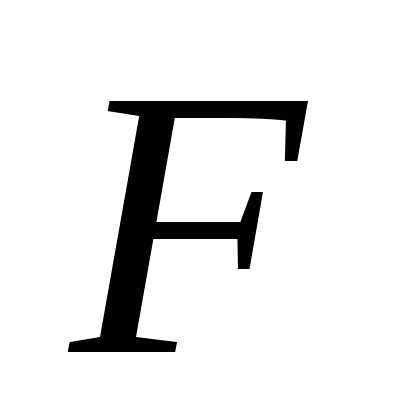в виде уравнения:
, (2)
Уравнениям (1) и (2) соответствует первая симплекс-таблица:
|
|
|
| ….. |
|
| ….. |
|
| |
| 0 | 1 | 0 | ….. | 0 |
| ….. |
|
| |
| 0 | 0 | 1 | ….. | 0 |
| ….. |
|
| (3) |
| ….. | ….. | ….. | ….. | ….. | ….. | ….. | ….. | ….. | |
| 0 | 0 | 0 | ….. | 1 |
| ….. |
|
| |
| 1 | 0 | 0 | ….. | 0 |
| ….. |
|
|
Начало алгоритма симплекс-метода.
Шаг 1. По симплекс-таблице находим опорное решение. На первом шаге это будет:
и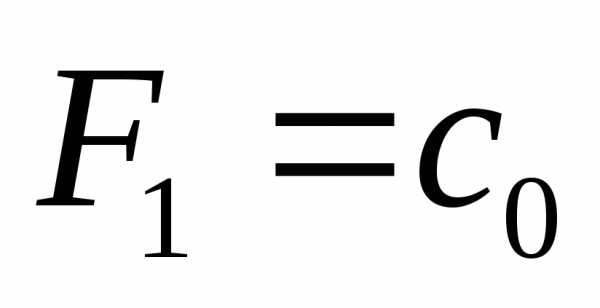 
(4)
Шаг 2. Проверяем условие оптимальности полученного опорного решения. Если последняя (индексная) строка таблицы (3) не содержит отрицательных элементов, то есть, все коэффициенты целевой функции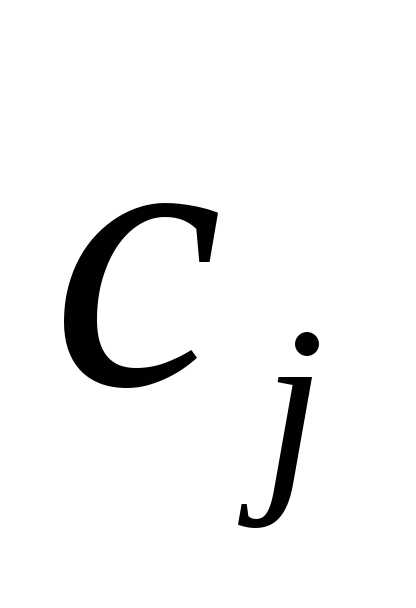 
неположительные:то опорное решение является оптимальным. Решение задачи заканчивается, и мы переходим к шагу 9.
Если условие оптимальности: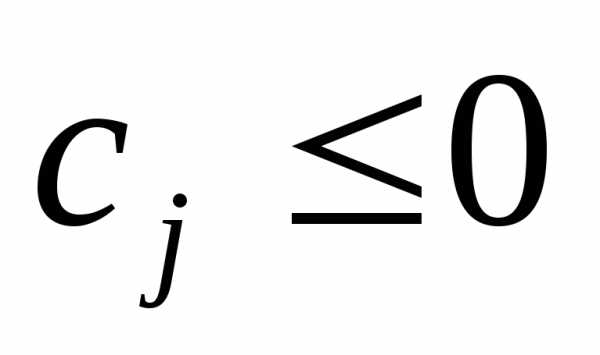 
, не выполнено, то продолжаем решение задачи.
Шаг 3. Выбираем номер 
одного из столбцов, содержащих отрицательные элементы в индексной строке. Соответствующий столбец объявляем ведущим.
Шаг 4. Определяем минимальное допустимое отношение 
для каждой строки по правилу:
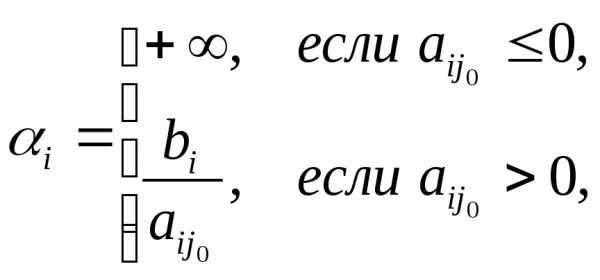
где 
- номер ведущего столбца.
Шаг 5. Выбираем номер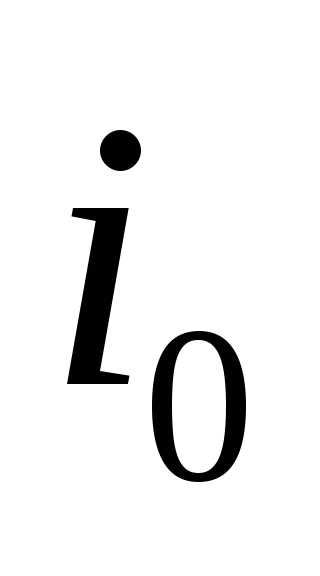 
ведущей строки с минимальным допустимым отношением
.
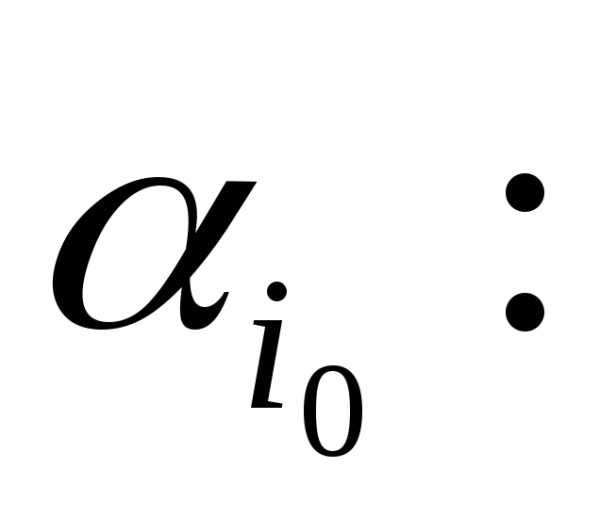Соответствующую строку называем ведущей. Если такой выбор невозможен, то есть все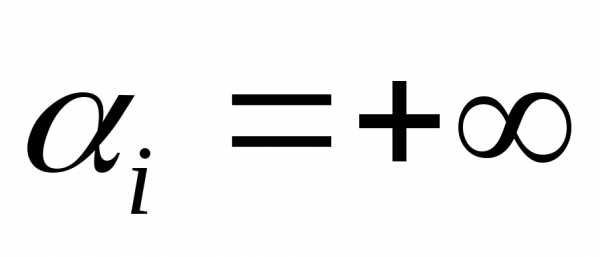 
, то заканчиваем решение, поскольку в этом случае задача не имеет решения. Переходим к шагу 10.
Шаг 6. Делим ведущую строку на ключевой элемент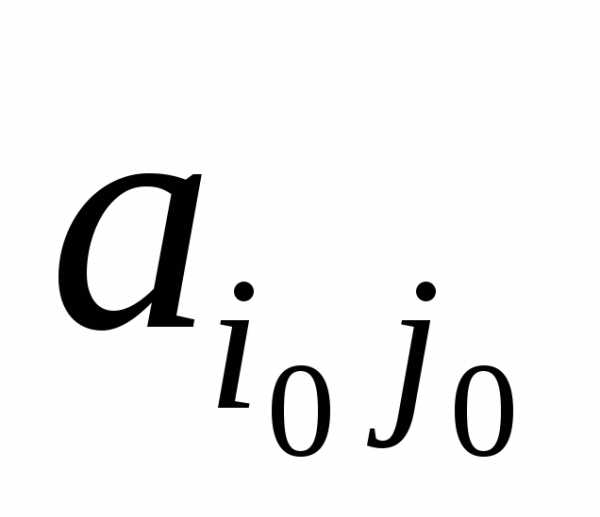 
, стоящий на пересечении ведущей строки и ведущего столбца. В результате на месте ключевого элемента
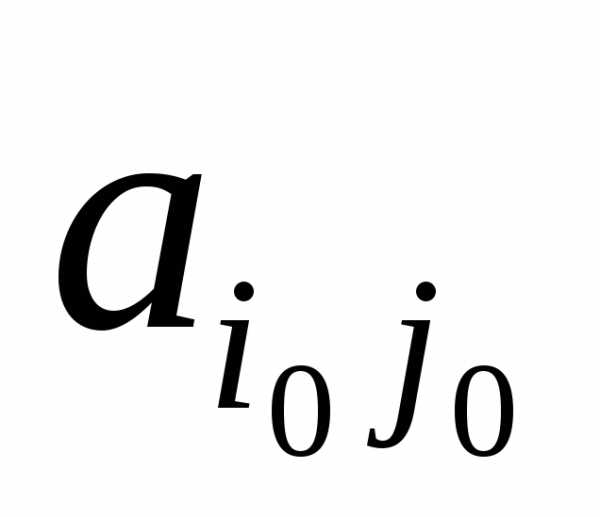получаем единицу:
.
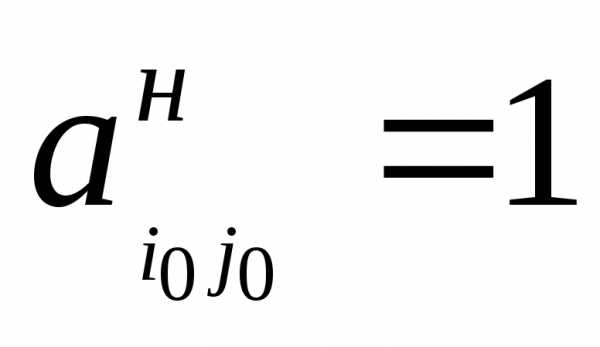Шаг 7. Из каждой строки таблицы, кроме ведущей, вычитаем ведущую строку, умноженную на элемент текущей строки, стоящий в ведущем столбце. В результате получаем, что все элементы ведущего столбца, кроме ключевого, равного единице, равны нулю, то есть ведущий столбец превратился в базисный. При этом оказывается, что один из базисных столбцов превратился в свободный (именно, тот, который содержал 1 в ведущей строке). Нами получена новая симплекс-таблица, отличающаяся от прежней набором базисных столбцов.
Шаг 8. Переходим к шагу 1.
Шаг 9. Объявляем, что получено оптимальное решение и выводим результаты решения. Затем переходим на конец алгоритма.
Шаг 10. Сообщаем, что задача не имеет решения и переходим на конец алгоритма.
Конец алгоритма.
1.9. Геометрическая интерпретация симплекс-метода.
Мы уже знакомы с геометрической интерпретацией задачи линейного программирования (п. 1.6.). Рассмотрим теперь симплекс-метод также с геометрической точки зрения. Суть дела проясняет следующая теорема.
Теорема. Каждое опорное решение канонической задачи ЛП. Является угловой точкой области допустимых решений. Наоборот, каждая угловая точка ОДР канонической задачи ЛП является опорным решением.
Доказательство. Докажем первое утверждение теоремы. Пусть 
- угловая точка. Пусть отрезок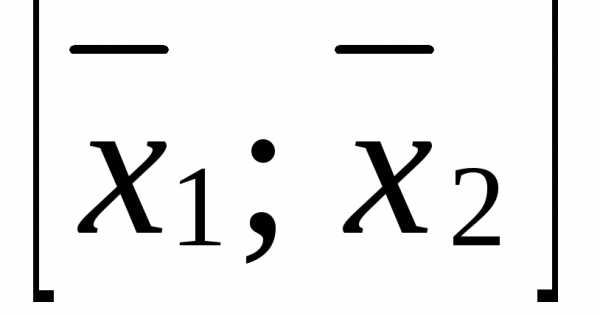
целиком лежит в ОДР, и его середина совпадает с
:
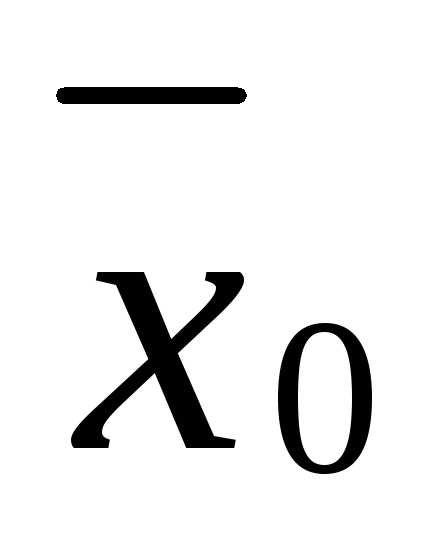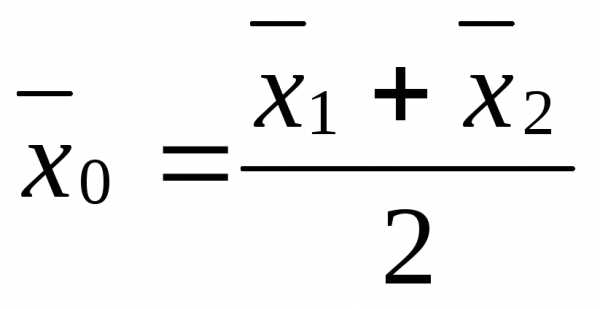(1)
Векторное равенство (1) равносильно системе равенств для координат
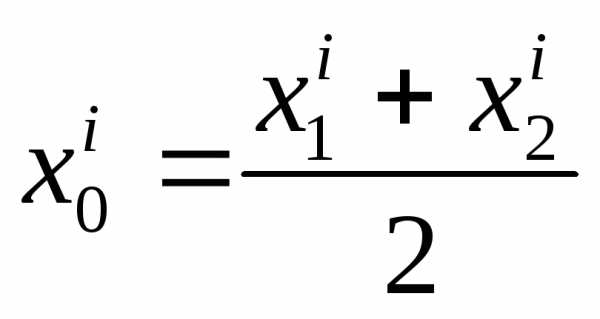(2)
Если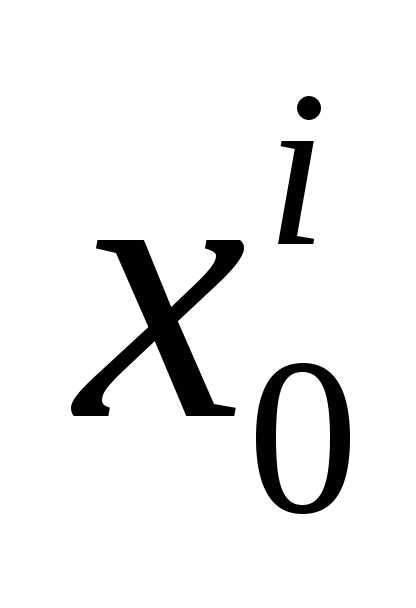 
- свободная переменная опорного решения
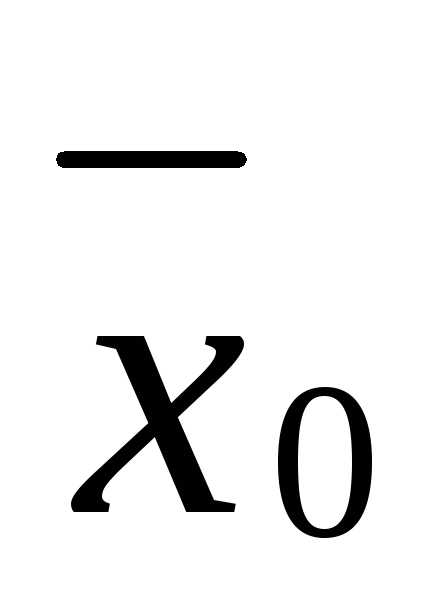, то из (2) следует, что
(3)
Поскольку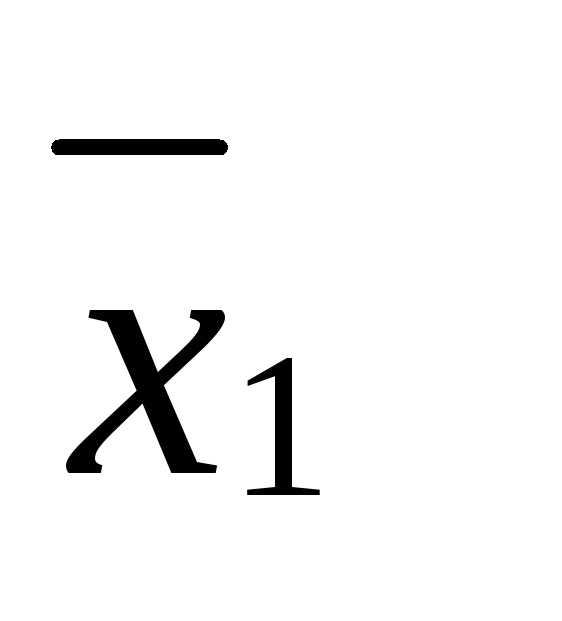 
и
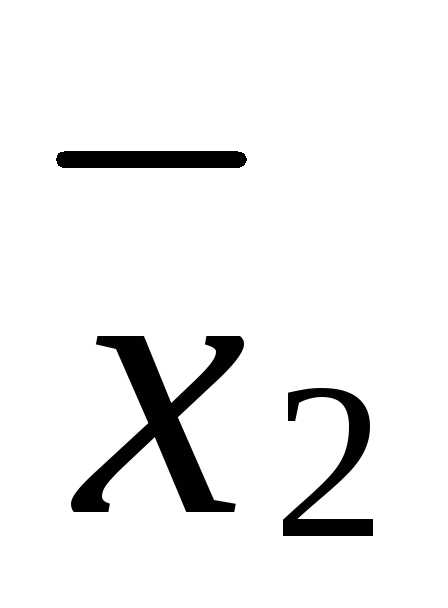- допустимые решения, то
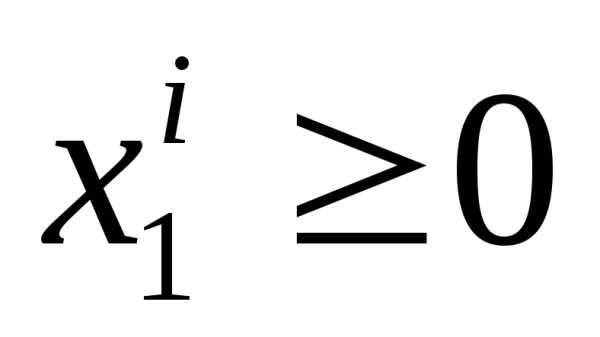и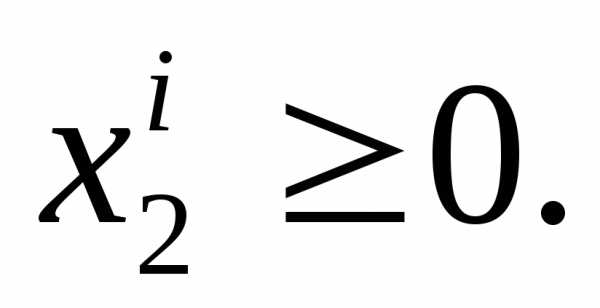
Сумма двух отрицательных чисел может равняться нулю, только, если эти числа сами равны нулю:
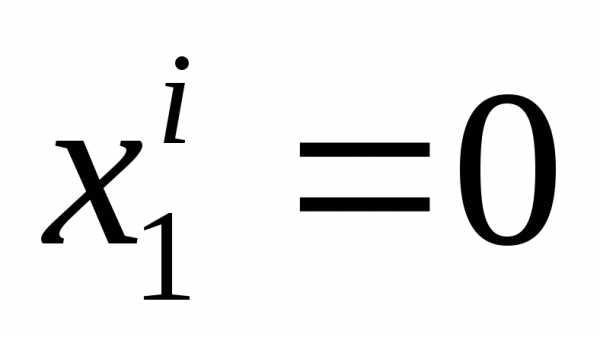и 
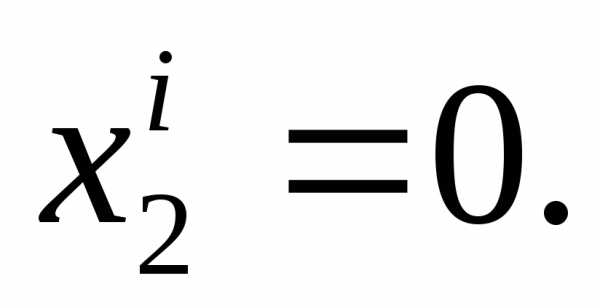(4)
Это означает, что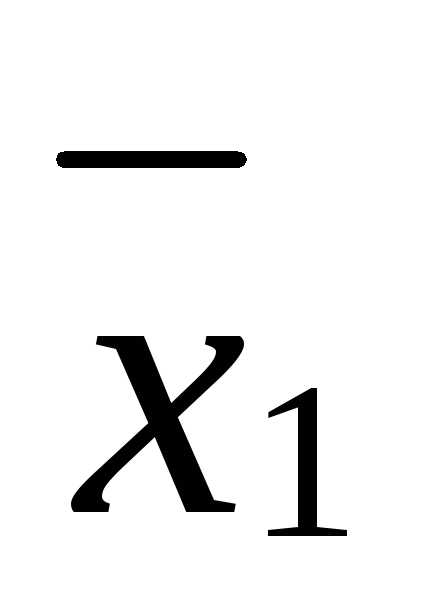 
и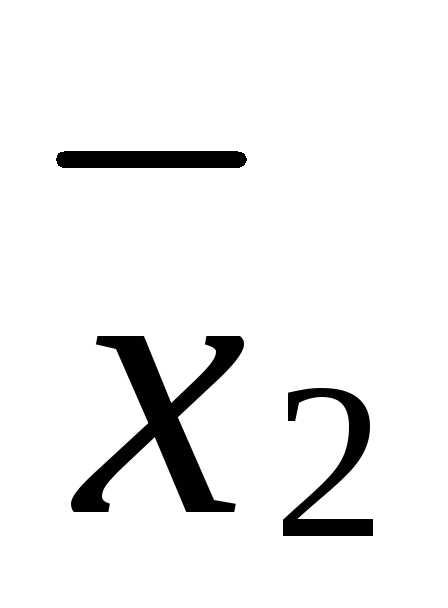
также являются опорными решениями с тем же набором свободных и, следовательно, базисных переменных. Но такое решение может быть только одно. Следовательно,, то есть отрезок
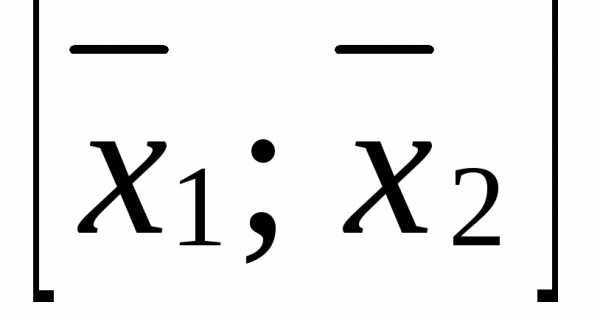, представляет из себя точку. Таким образом, мы показали, что не существует отрезка
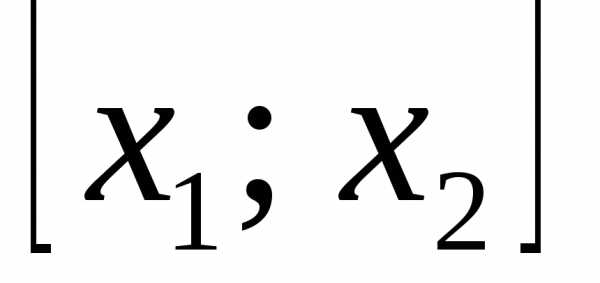целиком лежащего в ОДР и содержащего
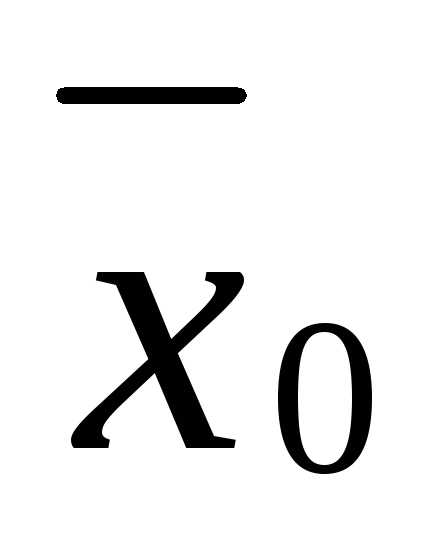в качестве своей внутренней точки. Утверждение доказано.
Доказательство второго утверждения довольно сложное и мы его не приводим.
Итак, мы видим, что симплекс-метод геометрически означает переход от одной угловой точки к другой, в которой значение целевой функции больше (или равно) предыдущему значению. Поскольку целевая функция растет только в направлении вектора роста, то движение по угловым точкам совершается в симплекс-методе в том же направлении.
studfiles.net
Алгоритм симплексного метода
Количество просмотров публикации Алгоритм симплексного метода - 579
Общая постановка задачи
Симплексный метод решения задач ЛП
Симплексный метод – метод последовательного улучшения плана.
Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования. Математическая модель задачи приводится к каноническому (стандартному) виду. Заполняется опорная симплекс – таблица с использованием коэффициентов целевой функции и системы ограничений. Решается задача по алгоритму.
Идея симплексного метода состоит по сути в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по допустимым решениям к оптимальному. Значение целевой функции для задач на максимум не убывает. Так как число допустимых решений конечно, то через конечное число шагов получим оптимальное решение.
1.Математическую модель задачи привести к каноническому (стандартному) виду.
2. Построить начальную симплекс-таблицу исходя из стандартного вида.
3. Найти разрешающий столбец.
В строке коэффициентов ЦФ найти значение с самим маленьким отрицательным числом. Этот столбец и будет разрешающим.
4. Вычислить разрешающую строку и ведущий элемент.
Почленно разделить столбец свободных членов на элементы разрешающего столбца, за исключением строки ЦФ. Выбрать наименьшее из частных. Эта строка будет разрешающей. Ведущий элемент будет на пересечении разрешающего столбца и разрешающей строки.
5.Построить новую симплекс-таблицу-второй шаᴦ.
При построении новой таблицы убрать из базиса строку с переменной разрешающей строки в предыдущей таблице. Ввести в базис строку с названием разрешающего столбца предыдущей таблицы.
-Построение ведущей строки в новой таблице.
Почленно поделить все элементы разрешающей строки на ведущий элемент.
-Построение других строк в новой таблице.
Почленно умножить ведущую строку на соответствующие этим строкам элементы разрешающего столбца из предыдущей таблицы и прибавить к соответствующим строкам в старой таблице.
6. Проверяем таблицу второго шага на оптимальность. В случае если в строке целевой функции нет отрицательных элементов, тогда таблица имеет оптимальный план, записать ответ. В случае если в строке ЦФ есть отрицательный элемент (элементы), тогда переходят к следующему (третьему) шагу, строят новую симплекс-таблицу в соответствии п.5 и затем проверяют ее на оптимальность. Построение таблиц заканчивается с нахождением оптимального плана.
Прямая задача на минимум решается следующим образом:
-Написать математическую модель двойственной задачи в стандартном виде
-Решить двойственную модель симплекс - методом
-Записать ответ.
Связь между задачами двойственной пары в том, что, решая симплексным методом одну из них, автоматически получаем решение другой.
Для этого достаточно воспользоваться соответствием переменных прямой и двойственной задач в последней симплекс-таблице.
| Х1 | x2 | … | xn | S1 | S2 | … | Sm |
| S1 | S2 | … | Sm | y1 | y2 | … | ym |
referatwork.ru
4 Переход от графического решения к алгебраическому. Алгоритм симплекс – метода. Вычислительный алгоритм симплекс-метода. - Математические методы исследования операций .Теория игр и расписаний.
Ограничения. Обозначим x1 и x2 соответственно количество порций пирога и гамбургеров. Можно ограничиться либо 200 фунтами мяса, либо докупить еще. В первом случае ограничение 0,25x1+0,2x2 200, во втором 0,25x1+0,2x2 200.
Естественно, выбор неравенства будет влиять на решение. Так как мы не знаем, какое ограничение необходимо, логично заменить их одним равенством 0,25x1+0,2x2-x3=200, где x3 –свободная переменная. Здесь она играет роль и избыточной, и остаточной.
Целевая функция. Раз надо максимизировать доход, надо продавать как можно больше продукции, то для этого нужны дополнительные закупки мяса, в этом случае x3 должна быть отрицательной, т.е. играть роль избыточной переменной. Для того, чтобы раскрыть «двойственную» природу переменной x3, представим ее в таком виде:
, где 0
Если >0 и , то переменная x3 играет роль остаточной. Если >0 и =0, то x3 выступает как избыточная. Итак ограничения теперь имеет вид
.
А целевая функция
Z=
Переход от графического решения к алгебраическому.
Идеи, лежащие в основе графического решения, лежат в основе алгебраического метода, который называется симплекс-методом. В графическом методе пространство решений определяется как пересечение полупространств, порождаемых ограничениями. В алгебраическом или симплекс-методе пространство решений задают m линейных уравнений и n неотрицательных переменных.
В алгебраическом представлении количество уравнений m всегда меньше или равно количеству переменных n. (Если количество уравнений m больше количества переменных n, тогда m-n уравнений избыточны.) Если m=n и система уравнений совместна, то она имеет одно решение (если она невырождена), если же m<n и система уравнений совместна, то она имеет бесконечное множество решений.
В алгебраическом представлении кандидаты на оптимальное решение (угловые точки в графическом представлении ) определяются из системы линейных уравнений следующим образом. Пусть m<n (это для большинства задач ЛП выполняется), тогда полагаем n-m переменных равным нулю и решаем систему из mуравнений относительно оставшихся m неизвестных, если решение единственно, то оно соответствует одной угловой точке пространства решений.
Пример. Z=2x1+3x2 max
2x1+x2 4
x1+2x2 5
x1,x2 0.
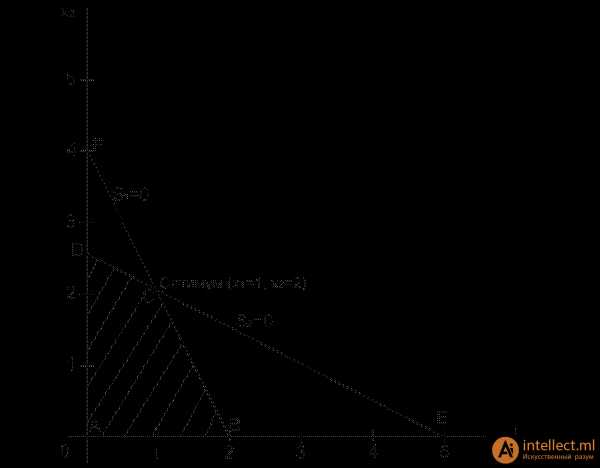
После преобразования к стандартной форме имеем следующую задачу ЛП.
Z=2x1+3x2 max
2x1+x2+S1 =4,
x1+2x2+S2=5,
x1, x2, S1, S2 0.
Имеем систему из m=2 уравнений для n=4 переменных. Как мы договорились, угловые точки можно определить алгебраически, присвоив n=m=4-2=2 переменным нулевые значения, а затем решив систему относительно m=2 переменных. Если положить x1=0 и x2=2 (точка C).
Какие же переменные полагать равными нулю, чтобы получить угловые точки? Надо просто рассмотреть все комбинации n-m переменных, приравнять их нулю и найти все угловые точки.
В нашем примере мы имеем угловых точек. На рисунке мы видим только 4. Где же еще две? В действительности точки E и F также являются угловыми точками. Но они еще не кандидаты на оптимальное решение, поскольку не удовлетворяют всем ограничениям.
Для полного перехода к алгебраическому методу решения задачи ЛП необходимо как-то назвать угловые точки разного типа. n-m переменных, которые полагают равными нулю называют небазисными переменными. Если оставшиеся m переменных имеют единственное решение, они называются базисными переменными, а совокупность решений, которые они дают составляют базисное решение. Если при этом все переменные принимают неотрицательные значения, такое базисное решение называют допустимым.
|
Небазисные (нулевые) переменные |
Базисные переменные |
Базисные решения |
Угловые точки |
Допустимо ли решение? |
Значение целевой функции Z |
|
(x1, x2) |
(S1, S2) |
(5, 4) |
A |
Да |
0 |
|
(x1, S1) |
(x2, S2) |
(4, -3) |
F |
Нет |
- |
|
(x1, S2) |
(x2, S1) |
(2.5, 1.5) |
D |
Да |
7,5 |
|
(x2, S1) |
(x1, S2) |
(2, 3) |
B |
Да |
4 |
|
(x2, S2) |
(x1, S1) |
(5, -6) |
E |
Нет |
- |
|
(S1, S2) |
(x1, x2) |
(1, 2) |
C |
Да |
8(опт.) |
Из этого примера видно, что при возрастании размерности задачи (n и m) процесс перечисления всех угловых точек задача становится очень сложной задачей. Например, при n=20 и m=10 необходимо решить 184756 систем уравнений порядка 1010. Это уже устрашающая вычислительная задача. Реально же m и n могут достигать сотен тысяч. Эту проблему снимает симплекс метод.
Алгоритм симплекс – метода.
Итак, процедура перебора всех базисных решений неэффективна. Рассмотрим симплекс – метод.
Итерационная природа симплекс – метода.
Рассмотрим пространство решений для того же примера.
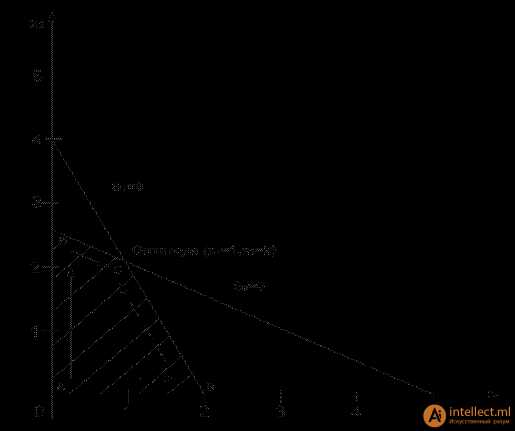
Обычно алгоритм симплекс – метода начинается с исходной точки, где x1=x2=0 (точка A). В этой начальной точке значение целевой функции Z равно нулю. Возникает вопрос: если одна или обе небазисные переменные x1 и x2 примут положительные значения, приведет ли это к улучшению целевой функции?
Z=2x1+3x2 max.
Очевидно, что если переменная x1 и x2 (или обе сразу ) примут положительные значения, то это приведет к увеличению значения ЦФ.
Однако алгоритм симплекс – метода на каждом шаге допускает изменение значения только одной небазисной переменной.
1. Если увеличивать значение переменной x1, то ее значение должно возрасти так, чтобы соответствовать угловой точке B (кандидаты – только угловые точки). В точкеB симплекс – метод должен увеличить значение переменной x2, перемещаясь в угловую точку C. Т.к. точка C соответствует оптимуму, то процесс заканчивается. Т.о. алгоритм симплекс – метода создает путь ABC.
2. Если сначала увеличивать значение переменной x2, то следующей угловой точкой будет точка D, из которой переходим в точку C и заканчиваем процесс ADC.
Отметим, что оба пути ABC и ADC расположены вдоль границы Г пространства решений. Т.о. симплекс – метод не может сразу перескочить из т.A в т.C.
Каждую же небазисную переменную сделать положительной в данной угловой точке? Если мы рассматриваем задачу максимизации, то следует выбирать такую небазисную переменную, которая имеет наибольший положительный коэффициент в выражении целевой функции. Если таких переменных несколько, то выбор произволен. Это правило эмпирическое.
Как переводить небазисные переменные в базисные и наоборот при переходе от одной угловой точки к другой?
На рисунке показано, что в точке А переменные S1 и S2 являются базисными, а переменные x1 и x2 – небазисными Если переменная x1 принимает положительное значение, мы переходим в угловую точку В, в которой изменяется состояние переменной x1 из небазисной в базисную. Одновременно переменная, которая была базисной в точке А становится небазисной и принимает нулевое значение в точке В. Здесь существенно, сто происходит одновременный «обмен состояниями» между небазисной переменной x1 и базисной S1, что приводит к новым базисным (x1,S2) и небазисным (S1,x2) переменным в точке В. В точке А переменная x1 вводится в базисное решение, а переменная S1 исключается из базисного решения. По терминологии симплекс-метода выбранная небазисная (нулевая) переменная называется вводимой (в базисное решение), а удаляемая (из базисного решения) базисная переменная исключаемой. В т. В вводимой и исключаемой переменными будутсоответственно x2 и S2.
Вычислительный алгоритм симплекс-метода.
Рассмотрим следующий пример.
Вернемся к задаче про компанию Reddy Mikks. В стандартной форме эта задача запишется так:
Z=5x1+4x2+0S1+0S2+0S3+0S4 max
при ограничениях:
6x1+4x2+S1=24
x1+2x2+S2=6
-x1+x2+S3=1
x2+S4=2
x1,x2,S1,S2,S3,S40
Здесь S1,S2,S3,S4 – дополнительные (остаточные) переменные.
Целевую функцию будем представлять в виде уравнения:
Z – 5x1 – 4x2 =0
Задачу ЛП в стандартной форме представим в виде таблицы:
|
Базис |
Z |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Решение |
|
|
Z |
1 |
- 5 |
- 4 |
0 |
0 |
0 |
0 |
0 |
Z-строка |
|
S1 |
0 |
6 |
4 |
1 |
0 |
0 |
0 |
24 |
S1-строка |
|
S2 |
0 |
1 |
2 |
0 |
1 |
0 |
0 |
6 |
S2-строка |
|
S3 |
0 |
-1 |
1 |
0 |
0 |
1 |
0 |
1 |
S3-строка |
|
S4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
S4-строка |
Таблица показывает множества базисных и небазисных переменных, а также решение, соответствующее данной (начальной) итерации. Начальная итерация начинается из точки (x1,x2)=(0,0). Это соответствует следующим множествам базисных и небазисных переменных:
Небазисные (нулевые): (x1,x2)
Базисные: (S1,S2,S3,S4)
Так как x1=0 , x2=0 и коэффициенты при базисных переменных S1,S2,S3,S4 в уравнении целевой функции равны нулю, а в формулах левых частей равенств ограничений – 1, то без дополнительных вычислений имеем: Z=0, S1=24, S2=6, S3=1, S4=0.
В таблице базисные переменные перечислены в левом столбце «Базис», а их значения – в правом столбце «Решение». Таким образом, определена текущая угловая точка.
Поскольку коэффициент при переменной x1 в формуле целевой функции наибольший, ее следует внести в число базисных (она станет вводимой). Из таблицы видно, что вводимая переменная определяется среди множества небазисных как имеющая наибольший отрицательный коэффициент во 2-й строке. Если все коэффициенты во 2-й строке будут неотрицательны, значит достигнут максимум.
Чтобы определить исключаемую переменную, надо вычислить точки пересечения всех функций с положительным направлением оси x1. Эти координаты можно вычислить как отношения правых частей равенства (столбец «Решение») и коэффициентов при переменной x1.
|
Базис |
Коэффициенты при x1 |
Решение |
Отношение (точка пересечения) |
|
S1 |
6 |
24 |
x1=24/6=4 |
|
S2 |
1 |
6 |
x1=6/1=6 |
|
S3 |
-1 |
1 |
x1=1/(-1)=-1 – не подходит |
|
S4 |
0 |
2 |
x1=2/0= – не подходит |
Максимальное неотрицательное соотношение соответствует базисной переменной S2, она определяется как исключаемая (т.е. на следующей итерации ее значение будет равно нулю). Значение вводимой переменной x1 также равно минимальному неотрицательному отношению: x1=6
Максимизировать
Z=5x1+4x2
1) 6x1+4x2+S1=24
2) x1+2x2+S2=6
3) -x1+x2+S3=1
4) x2+S4=2
x1,x2 0
Значение целевой функции при этом возрастет до 54=20.
Замена исключаемой переменной S1 на вводимую переменную x1 приводит к новым множествам базисных и небазисных переменных и к новому решению в т.В.
Небазисные (нулевые) переменные (S1,x2)
Базисные переменные (x1,S2,S3,S4)
Теперь надо выполнить преобразование в таблице, чтобы в столбцах «Базис» и «Решение» получить новое решение, соответствующее точке В.
В следующей таблице, которая пока совпадает с начальной определим ведущий столбец, ассоциируемый с вводимой переменной и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки называется ведущим.
|
Базис |
Z |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Решение |
|
|
Z |
1 |
- 5 |
- 4 |
0 |
0 |
0 |
0 |
0 |
|
|
S1 |
0 |
6 |
4 |
1 |
0 |
0 |
0 |
24 |
Ведущая строка |
|
S2 |
0 |
1 |
2 |
0 |
1 |
0 |
0 |
6 |
|
|
S3 |
0 |
-1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
|
S4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
|
Ведущий столбец
Процесс вычисления нового базисного решения состоит из двух этапов:
1. Вычисление элементов новой ведущей строки.
Новая ВС = Текущая ВС / Ведущий элемент
2. Вычисление элементов остальных строк, включая Z-строку.
Новая строка = Текущая строка – ее коэффициент в ведущем столбце Новая ВС
В примере вычисления таковы:
1. Новая ведущая S1-строка = Текущая ведущая S1-строка / 6
2. Новая Z-строка = Текущая Z-строка – (-5) Новая ВС
3. Новая S2-строка = Текущая S2-строка – (1) Новая ВС
4. Новая S3-строка = Текущая S3-строка – (-1) Новая ВС
5. Новая S4-строка = Текущая S4-строка – (0) Новая ВС
|
Базис |
Z |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Решение |
|
Z |
1 |
0 |
0 |
3/4 |
1/2 |
0 |
0 |
21 |
|
x1 |
0 |
1 |
0 |
1/4 |
-1/2 |
0 |
0 |
3 |
|
x2 |
0 |
0 |
1 |
-1/8 |
3/4 |
0 |
0 |
3/2 |
|
S3 |
0 |
0 |
0 |
3/8 |
-5/4 |
1 |
0 |
5/2 |
|
S4 |
0 |
0 |
0 |
1/8 |
-3/4 |
0 |
1 |
1/2 |
Так как Z-строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным S1 и S2, полученное решение оптимально.
Значения дополнительных переменных S1=S2=0, S3=5/2 и S4=1/2 согласуются со значениями переменных x1 и x2.
C помощью симплекс-таблицы можно получить много дополнительной информации о состоянии ресурсов. Статус «дефицитный» или «недефицитный» для ресурса определяется тем, использован он или нет. Если дополнительная переменная равна нулю, ресурс использован полностью, он получает статус дефицитного.
|
Ресурс |
Остаточная переменная |
Статус |
|
Сырье М1 |
S1=0 |
Дефицитный |
|
Сырье М2 |
S2=0 |
Дефицитный |
intellect.ml
Алгоритм симплекс-метода
Прежде чем решать ЗЛП симплекс-методом, её необходимо привести к канонической форме. После этого выделяют переменные, которые присутствуют только в одном уравнении и с коэффициентом «1», и принимают эти переменные в качестве базисных. Если в ограничении такую переменную выделить нельзя, то вводят искусственную базисную переменную. Затем определяется исходный базисный план и значение целевой функции для этого плана.
Шаги
1) Формирование начальной канонической формы и определение ДБР
Построение исходной симплекс-таблицы
№ итерации Таблица 2.3
| базис | B |
| … |
| … |
| … |
|
| ... | … | … | ||||||
|
|
|
|
| |||||
| ... | ||||||||
|
|
|
| … |
| ||||
| ... |
| … | ||||||
|
| 0 | -сj = -j |
В столбце «базис» записываются базисные переменные.
В последней строке столбца «базис» указывается функция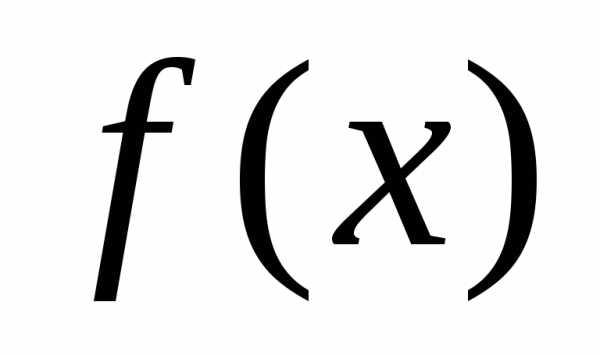 
.
В столбце «B» фиксируются свободные члены ограничений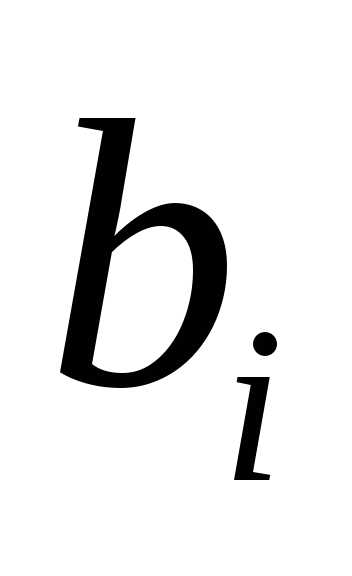
.
Bна 1-м этапе равно 0 (никакой прибыли).
Пример 2.5:
Рассмотрим пример 2.3 из предыдущего пункта.
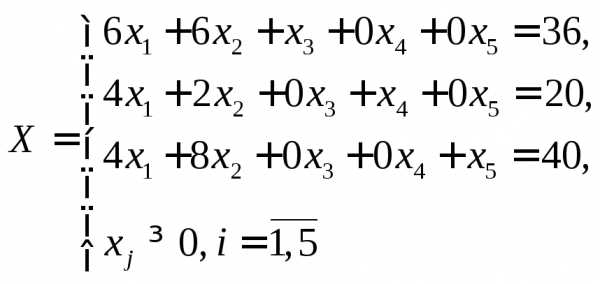
f(x) = 12x1+15x2 +0x3+0x4+0x5
В столбцах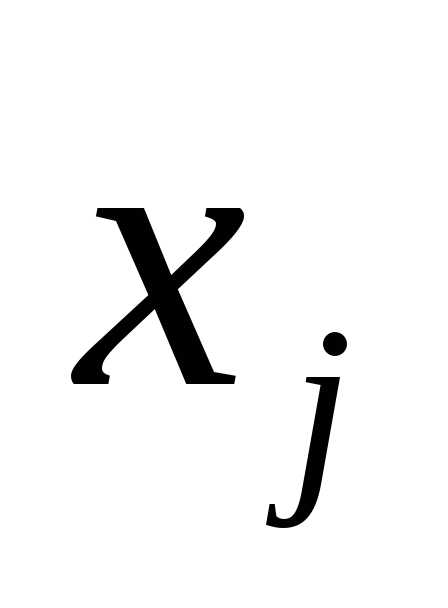 
для не базисных переменных отражаются коэффициенты при не базисных переменных в ограничениях (6,4,4)(6,2,8)
В столбцах базисных переменных содержится только 0 и 1 на пересечении столбца с соответствующей строкой базисной переменной
Последняя строка:
в «B» - значение целевой функции;
в остальных клетках - значение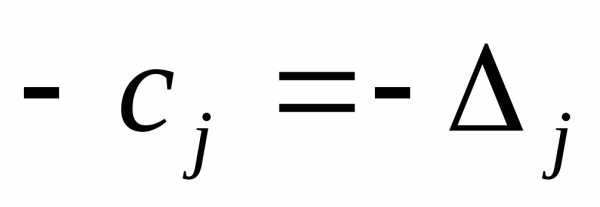 
из функции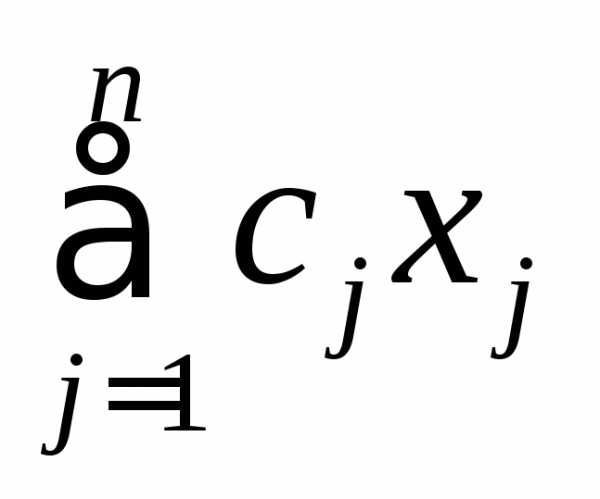
Таблица 2.4
| базис | В | х1 | х2 | х3 | х4 | х5 |
| х3 | 36 | 6 | 6 | 1 | 0 | 0 |
| х4 | 20 | 4 | 2 | 0 | 1 | 0 |
| х5 | 40 | 4 | 8 | 0 | 0 | 1 |
|
| 0 | -12 | -15 | 0 | 0 | 0 |
Проверка полученного базисного плана на оптимальность по условию оптимальности:
Если при каком-либо ДБР в симплекс-таблице все коэффициенты строки с f(x)(то есть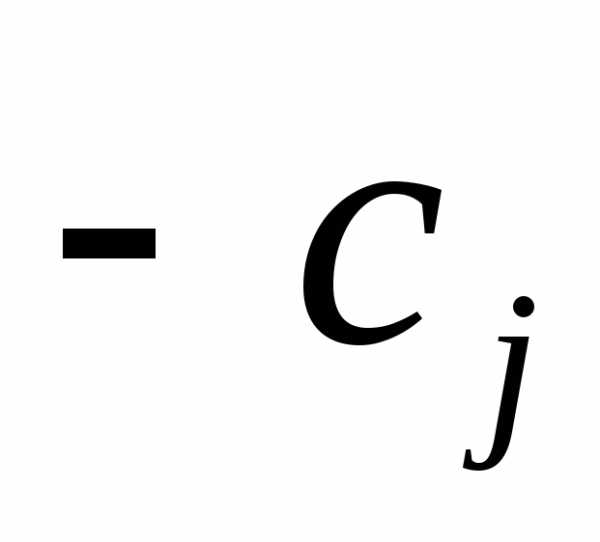
) не отрицательны, то данное ДБР оптимально.
Чтобы ДБР было оптимальным необходимо, чтобы среди базисных переменных не было искусственных
х5- является искусственной переменной, при этом все переменные от х1дох5больше или равны нулю.
Если для всех j, не принадлежащим базисным,
0, и среди базисных переменных есть искусственная, то задача неразрешима, так как её система ограничений несовместима.
Если 
0, то полученный базисный план не является оптимальным и необходимо переходить к другому базисному плану.
Если в оптимальном плане 
= 0 для не базисных переменных (х1, х2), то задача имеет бесконечное число планов.
Для перехода к новому базисному плану из числа небазисных переменных с отрицательными значениями
выбирается переменная, которая вводится в базис -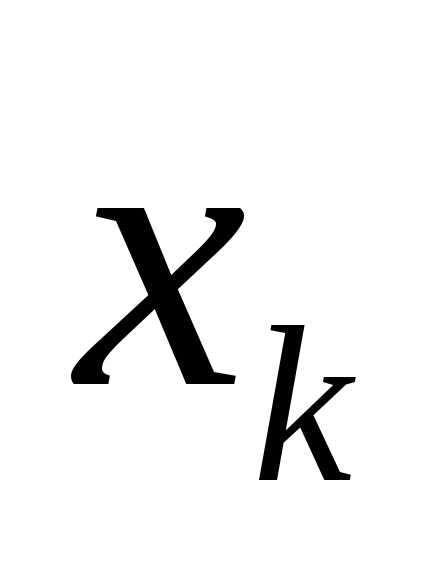 
, это переменная которой соответствует наибольшая по абсолютной величине отрицательная оценка
:
|k| =max|j| , среди
< 0,
=min
Столбец, отвечающий переменной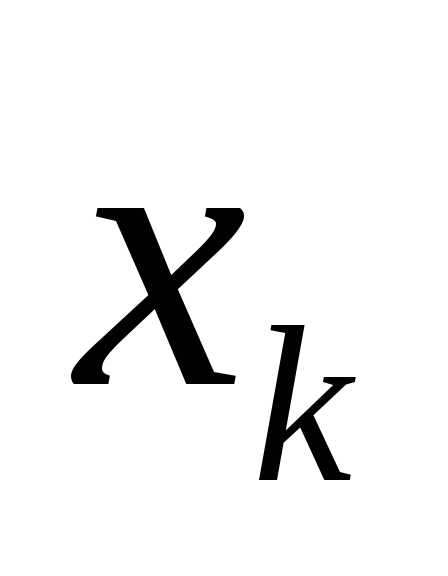 
, называется главным, или ведущим. Элементы этого столбца обозначаются через
.
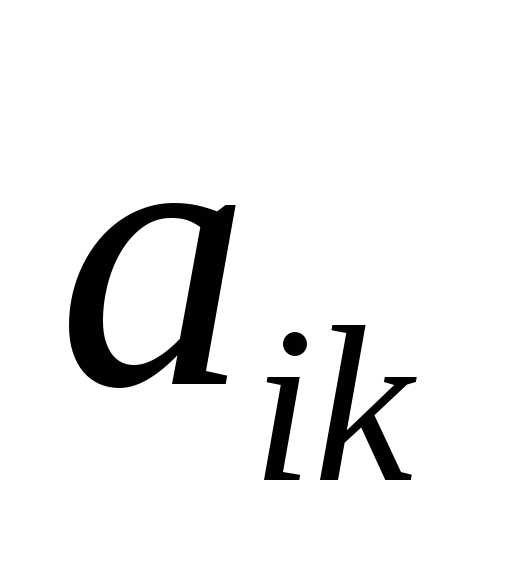Если окажется несколько одинаковых наибольших по абсолютной величине отрицательных оценок, то выбирается любая из соответственных переменных.
Выбираем переменную r- переменную, которая выводится из базиса. Данная переменная находится из соотношения
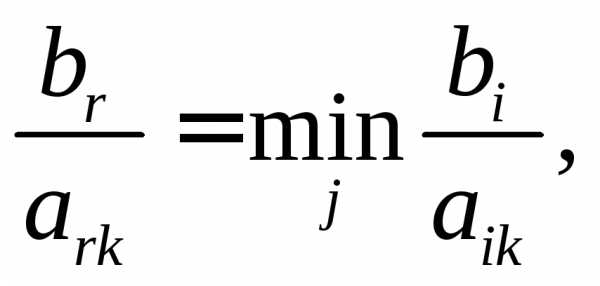(2.2)
≥ 0
Таблица 2.5
Для элементов ведущего столбца, которые больше 0, находим соотношение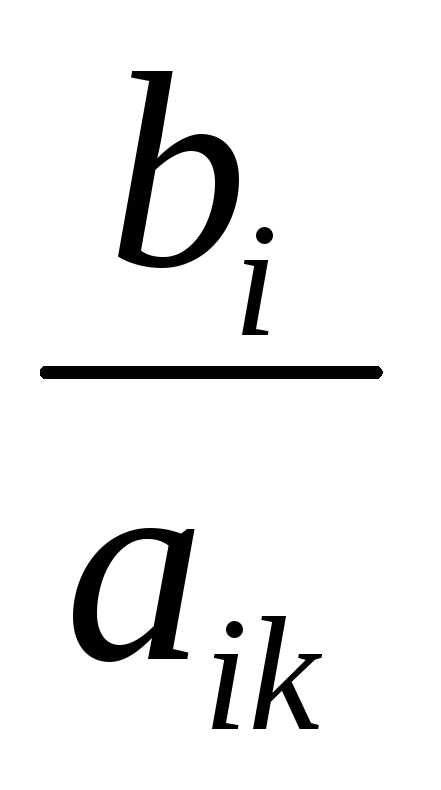 
и выбираем минимальное соотношение.
Строка таблицы, в которой получено наименьшее отношение элемента столбца «В» к соответствующему положительному элементу главного столбца, является главной, или ведущей.
Элементы главной строки обозначаются через 
. Выбранная переменная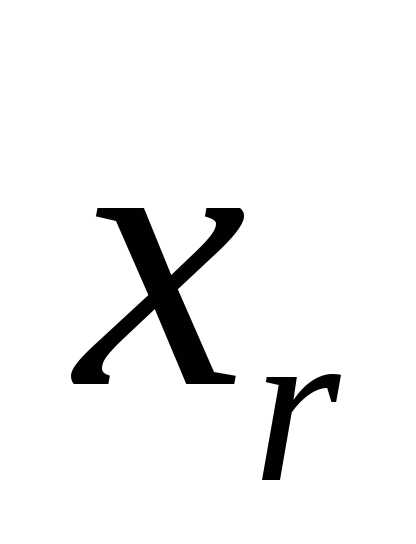
будет выводиться из базиса, то есть это исключаемая переменная.
Если окажется несколько одинаковых наименьших значений отношений, то выбирается любая из соответствующих им переменных.
Элемент, стоящий на пересечении главного столбца и строки называется главным, или ведущим, и обозначается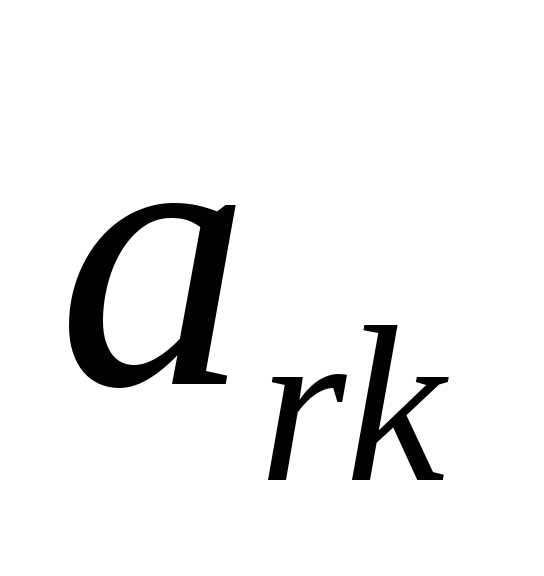 
В случае отсутствия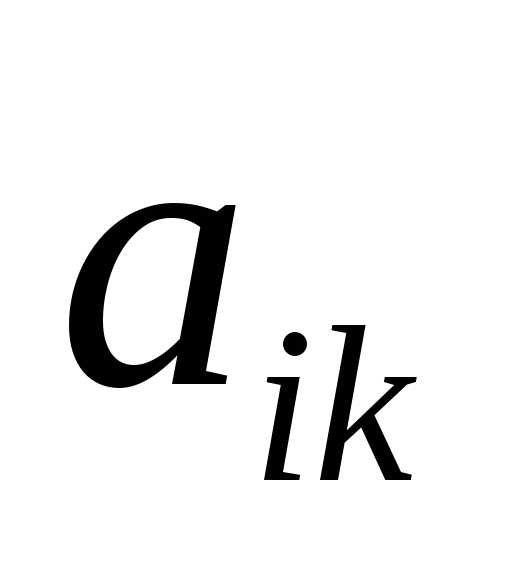 
0 задача неразрешима, то есть её целевая функция не ограничена на множестве планов задачи.
В примере 2.5:
Так как в строке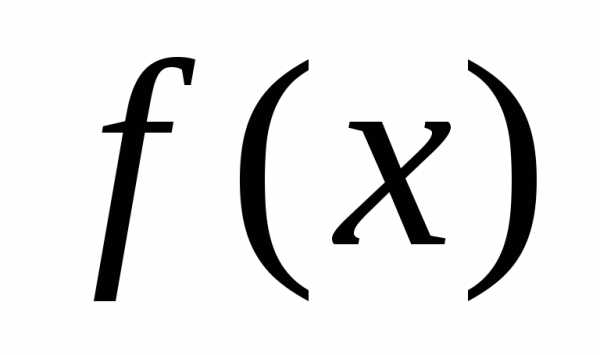 
минимальное значение -15, то вводимая переменная - х2и второй столбец является ведущим столбцом.
В столбце ищем элементы больше нуля, то есть 6, 2, 8, находим соотношения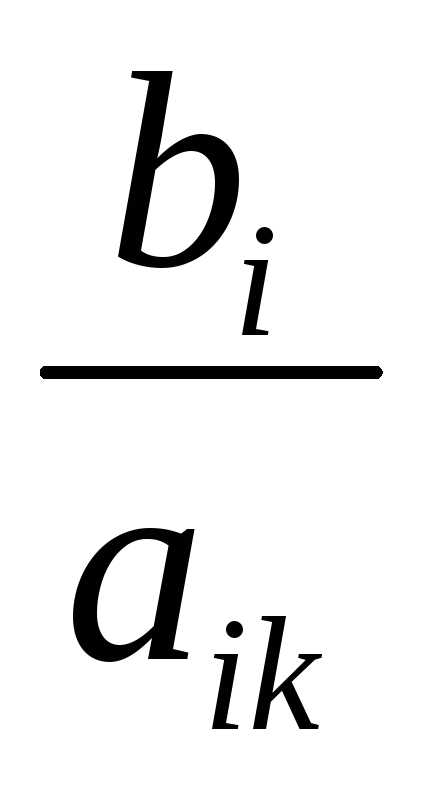 
, то естьвыбираем минимальное значение:
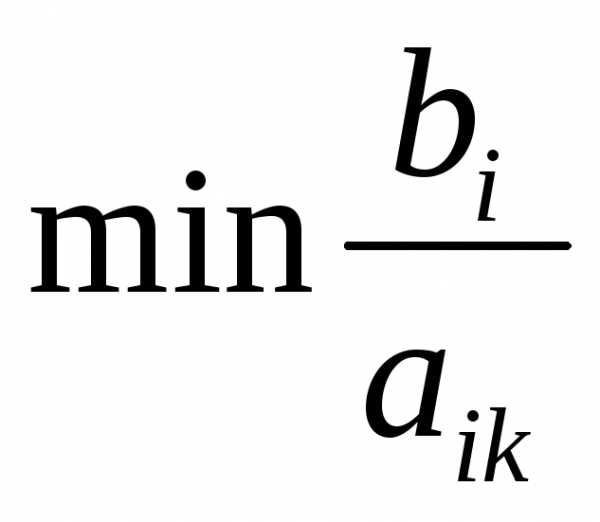соответствует третьей строке и переменной х5.
Следовательно, третья строка является главной строкой. Ведущий элемент 8.
Для определения нового базисного плана проводится пересчет элементов таблицы, и результаты заносятся в новую симплекс-таблицу. Выбранные переменные среди базисных и не базисных, лежащих на главной строке и главном столбце, меняются местами, то есть х2меняется с х5.
Процедура замены базиса осуществляется следующим образом:
а) элементы главной строки необходимо разделить на ведущий элемент
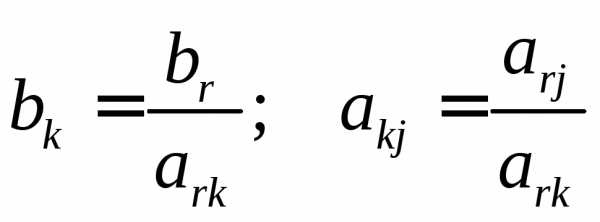(2.3)
б) элементы полученной строки умножаются на - 
, и результаты складываются сi-той строкой, причемi k.
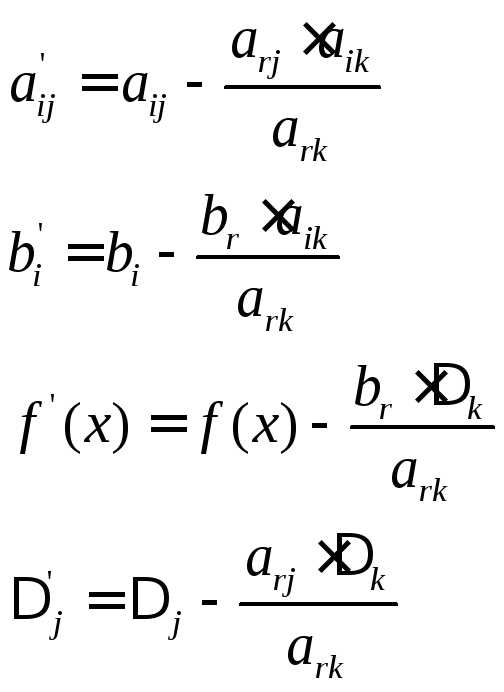(2.4)
Таблица 2.6
| базис | ЗН | х1 | х2 | х3 | х4 | х5 |
| х3 | 6 | 3 | 0 | 1 | 0 | -3/4 |
| х4 | 10 | 3 | 0 | 0 | 1 | -1/4 |
| х2 | 5 | 1/2 | 1 | 0 | 0 | 1/8 |
|
| 75 | -9/2 | 0 | 0 | 0 | 15/8 |
Строка при первой ведущей переменной получается из предыдущей строки делением на ведущий столбец, то есть на 8:
Строка с х2 (ведущая): 40 : 8 = 5;
4 : 8 = 1/2;
8 : 8 = 1;
0 : 8 = 0;
0 : 8 = 0;
1 : 8 = 1/8.
Строка с х3: 36 – 5 ∙ 6 = 6;
6 - 1/2 ∙ 6 = 3;
6 – 1 ∙ 6 = 0;
1 – 0 ∙ 6 =1;
0 – 0 ∙ 6 = 0;
0 – 1/8 ∙ 6 = -3/4.
Строка с х4: 20 – 5 ∙ 2 = 10;
4 - 1/2 ∙ 2 = 3;
2 – 1 ∙ 2 = 0;
0 – 0 ∙ 2 = 0;
1 – 0 ∙ 2 = 1;
0 – 1/8 ∙ 2 = -1/4
где 0 - предыдущее значение.
Коэффициенты целевой функции:
при
при
при
при
при
На следующей итерации выполняем аналогичные вычисления, и в результате получаем новую симплекс-таблицу
Таблица 2.7
| базис | ЗН | х1 | х2 | х3 | х4 | х5 |
| х1 | 2 | 1 | 0 | 1/3 | 0 | -1/4 |
| х4 | 4 | 0 | 0 | -1 | 1 | 1/2 |
| х2 | 4 | 0 | 1 | -1/6 | 0 | 1/4 |
|
| 84 | 0 | 0 | 3/2 | 0 | 3/4 |
Все коэффициенты в строке с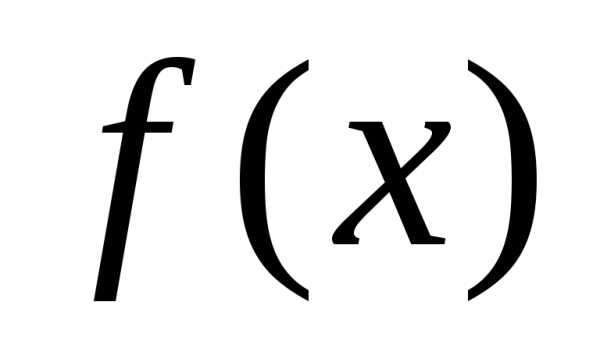
(
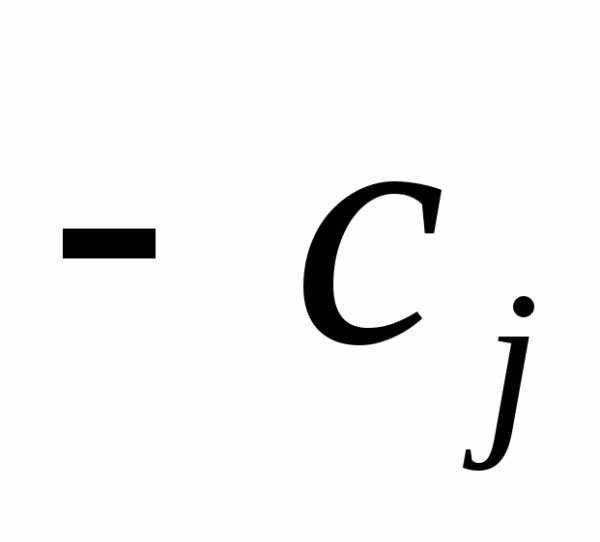) > 0, то есть это оптимальное значение.
Пример 2.6:
Рассмотрим пример 2.4 из предыдущего пункта.
Найдем наибольшее значение функции в заданной области, т.е. решим задачу линейного программирования (максимизируем линейную функцию при линейных ограничениях).
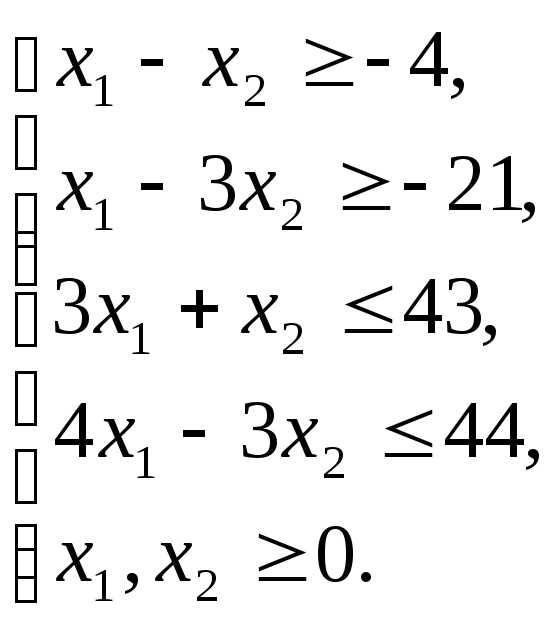
Приведем к канонической форме:
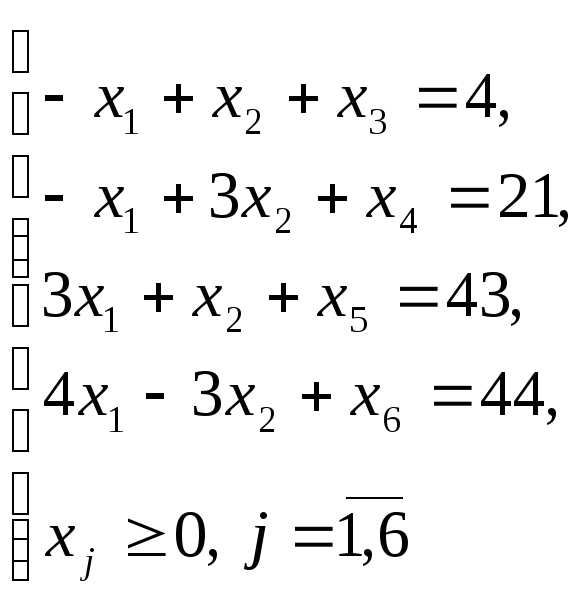
Исходная симплекс - таблица
Итерация №0 Таблица 2.8
| базис | значение | x1 | x2 | x3 | x4 | x5 | x6 |
| x3 | 4 | -1 | 1 | 1 | 0 | 0 | 0 |
| x4 | 21 | -1 | 3 | 0 | 1 | 0 | 0 |
| x5 | 43 | 3 | 1 | 0 | 0 | 1 | 0 |
| x6 | 44 | 4 | -3 | 0 | 0 | 0 | 1 |
| f (x) | 0 | -2 | -1 | 0 | 0 | 0 | 0 |
Переменную x1вводим в число базисных вместо переменнойx6
Ведущий элемент равен 4.
Итерация №1 Таблица 2.9
| базис | значение | x1 | x2 | x3 | x4 | x5 | x6 |
| x3 | 15 | 0 | 1/4 | 1 | 0 | 0 | 1/4 |
| x4 | 32 | 0 | 9/4 | 0 | 1 | 0 | 1/4 |
| x5 | 10 | 0 | 13/4 | 0 | 0 | 1 | -3/4 |
| x1 | 11 | 1 | -3/4 | 0 | 0 | 0 | 1/4 |
| f (x) | 22 | 0 | -5/2 | 0 | 0 | 0 | 1/2 |
Переменную x2вводим в число базисных вместо переменнойx5
Ведущий элемент равен 13/4.
Итерация №2 Таблица 2.10
| базис | значение | x1 | x2 | x3 | x4 | x5 | x6 |
| x3 | 185/13 | 0 | 0 | 1 | 0 | -1/13 | 4/13 |
| x4 | 326/13 | 0 | 0 | 0 | 1 | -9/13 | 10/13 |
| x2 | 40/13 | 0 | 1 | 0 | 0 | 4/13 | -3/13 |
| x1 | 173/13 | 1 | 0 | 0 | 0 | 3/13 | 1/13 |
| f (x) | 386/13 | 0 | 0 | 0 | 0 | 10/13 | -1/13 |
Переменную x6вводим в число базисных вместо переменнойx4
Ведущий элемент равен 10/13.
Итерация №3 Таблица 2.11
| базис | значение | x1 | x2 | x3 | x4 | x5 | x6 |
| x3 | 4,2 | 0 | 0 | 1 | -0,4 | 0,2 | 0 |
| x6 | 32,6 | 0 | 0 | 0 | 1,3 | -0,9 | 1 |
| x2 | 10,6 | 0 | 1 | 0 | 0,3 | 0,1 | 0 |
| x1 | 10,8 | 1 | 0 | 0 | -0,1 | 0,3 | 0 |
| f (x) | 32,2 | 0 | 0 | 0 | 0,1 | 0,7 | 0 |
Так как все значения 
> 0 , оптимальное значение найдено.
Ответ:
studfiles.net
Алгоритм двухэтапного симплекс-метода
Поиск ЛекцийКурсовая работа
по дисциплине «Программирование и основы алгоритмизации (Введение в исследование операций)»
Выполнила: Пагава Т.
Студентка 1 курса,
Гр. 1о-109с
Проверила: Топорова М.И.
Москва 2012г
Содержание
1. Условие задачи…………………………………………………………………………….. 3
2.Формализация задачи………………………………...……………………….. 3
3. Методы решения……………………………………………………………… 5
4.Решение задачи………………………………………………………………... 4
Симплекс метод ………………………………………………………….. 8
1. Условие задачи
Издательство, показатели деятельности которого отражены в таблице, выпускает литературу четырех серии.
| Показатель | Серия | |||
| Себестоимость единицы продукции, р./экз. Удельная пропускная способность типографии, оттиск/экз. Удельный расход бумаги, лист/экз. | 0,5 |
Прибыль от реализации ед. продукции (р./экз.) соответственно для каждой серии: 2,3,4,5. Издательство располагает финансовыми средствами в 10000р., лимитами на бумагу в размере 90000 лис. И пропускной способностью типографии, 110000 оттисков. Поступило предписание, что тиражи серий не должны быть менее 2000, 1300, 1500 и 1000 экз. соответственно. При каких тиражах выпускаемых серий издательство получит максимальную прибыль? Как изменится решения задачи, если у издательства появится возможность получить дополнительные финансовые средства? Насколько имеет смысл их увеличить?
2. Формализация задачи.
Требуется найти тиражи выпускаемых серий, при которых прибыль от их реализации максимальна.
В качестве критериальной функции L возьмем прибыль от реализации продукции. Таким образом, мы принимаем в качестве параметров, описывающих работу типографии тиражи соответствующих серий:
Х1 – тираж первой серии при этом X1≥ 2000
Х2 – тираж второй серии Х2≥ 1300 (1)
Х3 – тираж третий серии Х3≥1500
Х4 – тираж четвертой серии Х4≥1000
И
L=2х1+3Х2+4х3+5х4 (2)
Рассмотрим пропускную способность типографии, она равна 110000, мы принимаем в качестве параметров, описывающих количество оттисков на экземпляр при производстве:
Первого тиража – Х1
Второго тиража – 5Х2
Третьего тиража – 2Х3
Четвертого тиража – 2Х4
Поэтому:
Х1+5Х2+3Х3+2Х4 ≤ 110000 (3)
Рассмотрим ограничения на бюджет. Себестоимость тиража:
Первой серии – 0,5Х1
Второй серии – 4Х2
Третьей серии – Х3
Четвертой серии – 4Х4
При этом бюджет ограничен 10000 р.
Поэтому:
0,5Х1+2Х2+Х3+4Х4 ≤ 10000 (4)
Рассмотрим ограничения на бумагу: расход бумаги на тираж
Первой серии – 3Х1
Второй серии – 4Х2
Третьей серии – 2Х3
Четвертой серии – Х4
При этом лимит на бумагу 90000 л.
Поэтому
3Х1+4Х2+2Х3+Х4 ≤ 90000 л. (5)
Необходимо найти такие значения Х1, Х2, Х3, Х4, которые удовлетворяют ограничениям (1,3,4,5) и обеспечивают максимум критериальной функции (2)
Цель задачи – получение максимальной прибыли – может быть достигнута несколькими способами. Математическим выражением цели является критериальная (целевая) функция L, структура которой отражает вклад каждого из способов в достижении цели. В сформулированной задаче представлено n таких способов. Под способом достижения цели в сформулированной задаче понимается получение прибыли от одного тиража.
Коэффициент Сj представляет собой удельную прибыль при применении j-го способа достижения цели. (В нашем случае прибыль от реализации j-го типа тиража). Отсюда целевая функция также имеет стоимостное выражение.
Переменные Xj – искомые величины, представляющие собой интенсивность использования j-го способа достижения цели.
Для достижения цели имеется: m- виды ресурсов; bi – возможный объем потребления i-го ресурса. Коэффициент aij – это «расход» потребления i-го ресурса (пропускной способности) для производства j-го типа.
3. Методы решения
Данная задача относится к типу целочисленных.
Математическая модель целочисленной задачи:
Максимизировать
L=2Х1+3Х2+4Х3+5Х4
При ограничениях:
(1) 0,5Х1+2Х2+Х3+4Х4 ≤ 10000
3Х1+4Х2+2Х3+Х4 ≤ 90000
Х11+5Х2+3Х3+2Х4 ≤ 110000
Х1 ≥ 2000
Х2≥1300
Х3≥1500
Х4≥1000
ХJ ≥ 0. Целые j= 1,4
Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования, при их решении используются:
- методы отсечений
- методы разветвлений
- приближенные методы (даны допустимые решения, хотя и в общем случае неоптимальные)
- симплекс метод
-графический метод
- Двухэтапный симплекс (метод применяется к задачам, заданным не в канонической форме.)
Сформулированная ранее задача относится к классу задач целочисленного линейного программирования. Небольшая размерность задачи и то, что она не задана в канонической форме, позволяет нам применить двухэтапный симплекс метод.
4. Решение задачи
Прежде чем приступить к решению задачи запишем ее в общем виде:
(2) 0,5Х1+2Х2+Х3+4Х4+Х5 = 10000, Максимализировать
3Х1+4Х2+2Х3+Х4+Х6 = 90000,
Х11+5Х2+3Х3+2Х4+Х7=110000, L= СjXj
Х1 -Х8=2000, при ограничениях
Х2-Х9=1300,
Х3-Х10=1500, aij*Xj=bi
Х4-Х11=1000,
Где Xj≥0; j=1,…,11
Алгоритм двухэтапного симплекс-метода
1.
Привести задачу к стандартному виду. Если он является каноническим – решать одноэтапным симплекс-методом (см. 5)
2.
Составить вспомогательную задачу. Решить ее симплекс-методом.
3.
Если вспомогательная задача не имеет решения или по окончании решения получены ненулевые (положительные) коэффициенты в целевой функции вспомогательной задачи, то исходная задача не имеет решения, иначе см.4.
4.
Отбросить вспомогательную целевую функцию, выписать начальное допустимое базисное решение.
5.
Решить полученную каноническую задачу одноэтапным симплекс-методом.
(1.
Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных базисных переменных.(метод искусственного базиса).
2.
Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.
3.
Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делят на элементы того же знака ведущего столбца.
4.
Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.)
Воспользуемся искусственными переменными, решим следующую задачу (3).
(В качестве базиса мы можем взять только переменные Х5, Х6, Х7, нам не хватает еще четырех базисных переменных.)
L=2Х1+3Х2+4Х3+5Х4 max
0,5Х1+2Х2+Х3+4Х4+Х5 = 10000,
3Х1+4Х2+2Х3+Х4+Х6 = 90000,
Х11+5Х2+3Х3+2Х4+Х7=110000,
(3) Х1 -Х8+Х12=2000
Х2-Х9+Х13=1300
Х3-Х10+Х14=1500
Х4-Х11+Х15=1000
Х12, Х13, Х14, Х15 ≥0
Х1, Х2, Х3, Х4, Х5, Х6, Х7, Х8, Х9, Х10, Х11 ≥0
Если эта задача достигает оптимума при нулевых значения искусственных переменных (Х12 - Х15), тогда исходная задача (2) имеет решение и оно совпадает с решением (3).
Воспользуемся двухэтапным методом.
На первом этапе будем минимизировать сумму искусственных переменных ( если в результате мы получим ноль, значит задача (2) имеет решение, при этом мы найдем начальный опорный план и сможем перейти ко второму этапу. Что бы минимизировать сумму мы максимизируем W=-(-Х12+Х13+Х14+Х15).
Применим двухэтапный симплекс метод.
Исходными данными в подпрограмме является:
1) Размерность матрицы A=min
m=7, n=15
2) 0,5 2 1 4 1 0 0 0 0 0 0 0 0 0 0
3 4 2 1 0 1 0 0 0 0 0 0 0 0 0
1 5 3 2 0 0 1 0 0 0 0 0 0 0 0
A= 1 0 0 0 0 0 0 -1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 -1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 -1 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 -1 0 0 0 0
3) Вектор свободных членов в уравнении ограничений bi, i=1…m
=10000, 90000, 110000, 2000, 1300, 1500, 1000, 0, -5800
4) Коэффициент при переменных в критериальной функции Сj
J= 1 … n
= (2,3,4,5,0,0,0,0,0,0,0,0,0,0,0)
poisk-ru.ru
