ГлавнаяРазноеЧетная и нечетная функция

Четные и нечетные функции. Периодические функции. Четная и нечетная функция


Четность-нечетность функции. Период функции

Способы задания функции

Пусть функция задается формулой: y=2x^{2}-3. Назначая любые значения независимой переменной x, можно вычислить, пользуясь данной формулой соответствующие значения зависимой переменной y. Например, если x=-0,5, то, пользуясь формулой, получаем, что соответствующее значение y равно y=2 \cdot (-0,5)^{2}-3=-2,5.

Взяв любое значение, принимаемое аргументом x в формуле y=2x^{2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:

x−2−10123
y−4−3−2−101

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x. Наиболее часто, это будет приближенное значение функции.

Четная и нечетная функция

Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy.

Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. Такая функция будет симметрична относительно начала координат O (0;0).

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

f(x)=3x^{3}-7x^{7}

D(f)=(-\infty ; +\infty ) с симметричной областью определения относительно начала координат. f(-x)= 3 \cdot (-x)^{3}-7 \cdot (-x)^{7}= -3x^{3}+7x^{7}= -(3x^{3}-7x^{7})= -f(x).

Значит, функция f(x)=3x^{3}-7x^{7} является нечетной.

Периодическая функция

Функция y=f(x), в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x), называется периодической функцией с периодом T \neq 0.

Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T.

Промежутки, где функция положительная, то есть f(x) > 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.

f(x) > 0 на (x_{1}; x_{2}) \cup (x_{3}; +\infty )

Промежутки, где функция отрицательная, то есть f(x) < 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x) < 0 на (-\infty; x_{1} ) \cup (x_{2}; x_{3} )

Ограниченность функции

Ограниченной снизу принято называть функцию y=f(x), x \in X тогда, когда существует такое число A, для которого выполняется неравенство f(x) \geq A для любого x \in X.

Пример ограниченной снизу функции: y=\sqrt{1+x^{2}} так как y=\sqrt{1+x^{2}} \geq 1 для любого x.

Ограниченной сверху называется функция y=f(x), x \in X тогда, когда существует такое число B, для которого выполняется неравенство f(x) \neq B для любого x \in X.

Пример ограниченной снизу функции: y=\sqrt{1-x^{2}}, x \in [-1;1] так как y=\sqrt{1+x^{2}} \neq 1 для любого x \in [-1;1].

Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0, для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X.

Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1.

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).

а) Если при x > 0 четная функция возрастает, то убывает она при x < 0

б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0

г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0

Экстремумы функции

Точкой минимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняться неравенство f(x) > f(x_{0}). y_{min} - обозначение функции в точке min.

Точкой максимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняется неравенство f(x) < f(x^{0}). y_{max} - обозначение функции в точке max.

Необходимое условие

Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x), что дифференцируема в точке x_{0}, появится экстремум в этой точке.

Достаточное условие

  1. Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
  2. x_{0} - будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}.

Наибольшее и наименьшее значение функции на промежутке

Шаги вычислений:

  1. Ищется производная f'(x);
  2. Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b];
  3. Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.

academyege.ru

Нечётные и чётные функции | Математика

Файл:Function-x.svg Файл:Function x^2.svg

Нечётная фу́нкция — это функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

    • Функция $ f:[-X,X] \subset \mathbb{R} \to \mathbb{R} $ называется нечётной, если справедливо равенство
    $ f(-x)=-f(x), \quad \forall x \in [-X,X]. $
    • Функция $ f $ называется чётной, если выполнено равенство
    $ f(-x) = f(x),\quad \forall x \in [-X,X]. $
    • Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
    • График нечётной функции симметричен относительно начала координат $ O $.
    • График чётной функции симметричен относительно оси ординат $ Oy $.
    • Произвольная функция $ f:[-X,X] \subset \mathbb{R} \to \mathbb{R} $ может быть представлена в виде суммы нечётной и чётной функций:
    $ f(x) = g(x) + h(x), $

    где

    $ g(x) = \frac{f(x) - f(-x)}{2},\; h(x) = \frac{f(x)+f(-x)}{2}. $
    • Функция $ f(x) \equiv 0 $ — единственная функция, одновременно являющаяся нечётной и чётной.
    • Сумма двух нечётных функций сама нечётна.
    • Сумма двух чётных функций сама чётна.
    • Произведение или дробь двух нечётных функций чётно.
    • Произведение или дробь двух чётных функций чётно.
    • Произведение или дробь нечётной и чётной функций нечётно.
    • Композиция двух нечётных функция нечётна.
    • Композиция двух чётных функций чётна.
    • Композиция чётной функции с нечётной чётна.
    • Композиция любой функции с чётной чётна (но не наоборот).

    Нечётные функцииПравить

    • функции с нечетными степенями
    • .y=sin x, y=tg x, y=ctg x

    Чётные функцииПравить

    • Чётная степень $ f(x) = x^{2k},\quad x\in \mathbb{R} $ где $ k\in \mathbb{Z} $ — произвольное целое число.

    Вариации и обобщенияПравить

    cs:Sudé a liché funkcefa:توابع زوج و فردhe:פונקציות זוגיות ואי-זוגיות hu:Páros és páratlan függvényekpl:Funkcje parzyste i nieparzysteth:ฟังก์ชันคู่และฟังก์ชันคี่ uk:Непарна функція

    ru.math.wikia.com

    Четные и нечетные функции. Периодические функции

     

    Определение 1. Функция называется четной (нечетной), если вместе с каждым значением переменной значение –х также принадлежит и выполняется равенство

    (11.1)

    Таким образом, функция может быть четной или нечетной только тогда, когда ее область определения симметрична относительно начала координат на числовой прямой (числа х и –х одновременно принадлежат ). Например, функция не является четной и нечетной, так как ее область определения не симметрична относительно начала координат.

    Функция четная, так как симметрична относительно начала координат и .

    Функция нечетная, так как и .

    Функция не является четной и нечетной, так как хотя и симметрична относительно начала координат, равенства (11.1) не выполняются. Например, .

    График четной функции симметричен относительно оси Оу, так как если точка принадлежит графику, то и точка тоже принадлежит графику. График нечетной функции симметричен относительно начала координат, так как если принадлежит графику, то и точка тоже принадлежит графику.

    При доказательстве четности или нечетности функции бывают полезны следующие утверждения.

    Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).

    б) Произведение двух четных (нечетных) функций есть функция четная.

    в) Произведение четной и нечетной функций есть функция нечетная.

    г) Если f – четная функция на множестве Х, а функция g определена на множестве , то функция – четная.

    д) Если f – нечетная функция на множестве Х, а функция g определена на множестве и четная (нечетная), то функция – четная (нечетная).

    Доказательство. Докажем, например, б) и г).

    б) Пусть и – четные функции. Тогда , поэтому . Аналогично рассматривается случай нечетных функций и .

    г) Пусть f – четная функция. Тогда .

    Остальные утверждения теоремы доказываются аналогично. Теорема доказана.

    Теорема 2. Любую функцию , заданную на множестве Х, симметричном относительно начала координат, можно представить в виде суммы четной и нечетной функций.

    Доказательство. Функцию можно записать в виде

    .

    Функция – четная, так как , а функция – нечетная, поскольку . Таким образом, , где – четная, а – нечетная функции. Теорема доказана.

    Определение 2. Функция называется периодической, если существует число , такое, что при любом числа и также принадлежат области определения и выполняются равенства

    .

    Такое число T называется периодом функции .

    Из определения 1 следует, что если Т – период функции , то и число –Т тожеявляется периодом функции (так как при замене Т на –Т равенство сохраняется). С помощью метода математической индукции можно показать, что если Т – период функции f, то и , тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.

    Определение 3. Наименьший из положительных периодов функции называется ее основным периодом.

    Теорема 3. Если Т – основной период функции f, то остальные периоды кратны ему.

    Доказательство. Предположим противное, то есть что существует период функции f ( >0), не кратный Т. Тогда, разделив на Т с остатком, получим , где . Поэтому

    ,

    то есть – период функции f, причем , а это противоречит тому, что Т – основной период функции f. Из полученного противоречия следует утверждение теоремы. Теорема доказана.

    Хорошо известно, что тригонометрические функции являются периодическими. Основной период и равен , и . Найдем период функции . Пусть - период этой функции. Тогда

    (так как .

    Отсюда

    или или или .

    Значение T, определяемое из первого равенства, не может быть периодом, так как зависит от х, т.е. является функцией от х, а не постоянным числом. Период определяется из второго равенства: . Периодов бесконечно много, при наименьший положительный период получается при : . Это – основной период функции .

    Примером более сложной периодической функции является функция Дирихле

    Заметим, что если T – рациональное число, то и являются рациональными числами при рациональном х и иррациональными при иррациональном х. Поэтому

    при любом рациональном числе T. Следовательно, любое рациональное число T является периодом функции Дирихле. Ясно, что основного периода у этой функции нет, так как есть положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное число можно сделать выбором n сколь угодно близким к нулю).

    Теорема 4. Если функция f задана на множестве Х и имеет период Т, а функция g задана на множестве , то сложная функция тоже имеет период Т.

    Доказательство. Имеем , поэтому

    ,

    то есть утверждение теоремы доказано.

    Например, так как cos x имеет период , то и функции имеют период .

    Определение 4. Функции, не являющиеся периодическими, называются непериодическими.

     

    Обратная функция

     

    Пусть – некоторая функция, и - ее область определения и область значений соответственно. Если любым различным значениям аргумента соответствуют различные значения функции, то есть из , , то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение множества на множество . Это отображение называется обратной функцией к функции , то есть обратная функция такова, что . Функция и обратная для нее функция называются взаимно-обратными функциями. Заметим, что , а графики взаимно-обратных функций и симметричны относительно прямой – биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз.

    Чтобы найти аналитическое выражение для функции , обратной к функции , нужно решить уравнение относительно х, и если при этом получается несколько значений х, то выбрать те значения, которые принадлежат . Таким образом получают равенство , в котором обычно заменяют у на х и х на у.

    Обратные функции для функций нужно рассмотреть на практических занятиях.

    функцию. Найдем ее. Имеем т.е. Отметим, что каждое свое
    Заметим, что условие строгой монотонности функции является достаточным, но не необходимым условием существования обратной функции. Пусть, например, Эта функция не монотонна на , однако имеет обратную

    значение функция принимает только один раз (такие функции называются инъективными).

    Похожие статьи:

    poznayka.org

    Чётность функции — WiKi

    Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

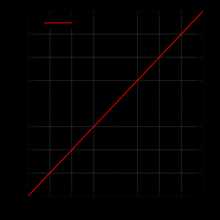    f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная
    • Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
    • Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
    • Ни чётная, ни нечётная функция (функция общего вида). В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

    Определения вводятся для любой симметричной относительно нуля области определения X⊂R{\displaystyle X\subset \mathbb {R} } , например, отрезка или интервала.

    • Функция f:X→R{\displaystyle f:X\to \mathbb {R} }  называется чётной, если справедливо равенство
    f(−x)=f(x),∀x∈X.{\displaystyle f(-x)=f(x),\quad \forall x\in X.} 
    • Функция называется нечётной, если справедливо равенство
    f(−x)=−f(x),∀x∈X.{\displaystyle f(-x)=-f(x),\quad \forall x\in X.} 
    • Функции, не принадлежащие ни одной из категорий выше, называются ни чётными, ни нечётными (или функциями общего вида).

    ru-wiki.org

    Чётные и нечётные функции Википедия

    Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

    f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная
    • Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
    • Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
    • Ни чётная, ни нечётная функция (функция общего вида). В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

    Строгое определение

    Определения вводятся для любой симметричной относительно нуля области определения X⊂R{\displaystyle X\subset \mathbb {R} }, например, отрезка или интервала.

    • Функция f:X→R{\displaystyle f:X\to \mathbb {R} } называется чётной, если справедливо равенство
    f(−x)=f(x),∀x∈X.{\displaystyle f(-x)=f(x),\quad \forall x\in X.}
    • Функция называется нечётной, если справедливо равенство
    f(−x)=−f(x),∀x∈X.{\displaystyle f(-x)=-f(x),\quad \forall x\in X.}
    • Функции, не принадлежащие ни одной из категорий выше, называются ни чётными, ни нечётными (или функциями общего вида).

    Свойства

    • График нечётной функции симметричен относительно начала координат O{\displaystyle O}.
    • График чётной функции симметричен относительно оси ординат Oy{\displaystyle Oy}.
    • Произвольная функция f:[−X,X]⊂R→R{\displaystyle f:[-X,X]\subset \mathbb {R} \to \mathbb {R} } может быть единственным образом представлена в виде суммы нечётной и чётной функций:
    f(x)=g(x)+h(x),{\displaystyle f(x)=g(x)+h(x),} где g(x)=f(x)−f(−x)2,h(x)=f(x)+f(−x)2.{\displaystyle g(x)={\frac {f(x)-f(-x)}{2}},\;h(x)={\frac {f(x)+f(-x)}{2}}.}
    • Функция f(x)≡0{\displaystyle f(x)\equiv 0} — единственная функция, одновременно являющаяся нечётной и чётной.
    • Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна. Поэтому чётные функции образуют линейное векторное пространство над полем действительных чисел, это же справедливо и для нечётных функций.
    • Произведение двух функций одной чётности чётно.
    • Произведение двух функций разной чётности нечётно.
    • Композиция двух нечётных функций нечётна.
    • Композиция чётной функции с нечётной чётна.
    • Композиция любой функции с чётной чётна (но не наоборот).
    • Производная чётной функции нечётна, а нечётной — чётна.
    • Для определённых интегралов от чётных функций выполняется равенство
    ∫−AAf(x)dx=2∫0Af(x)dx=2∫−A0f(x)dx.{\displaystyle \int \limits _{-A}^{A}f(x)\;dx=2\int \limits _{0}^{A}f(x)\;dx=2\int \limits _{-A}^{0}f(x)\;dx.} Соответственно, для определённых интегралов от нечётных функций выполняется равенство ∫−AAf(x)dx=0.{\displaystyle \int \limits _{-A}^{A}f(x)\;dx=0.}∫−∞∞f(x)dx=2∫0∞f(x)dx=2∫−∞0f(x)dx{\displaystyle \int \limits _{-\infty }^{\infty }f(x)\;dx=2\int \limits _{0}^{\infty }f(x)\;dx=2\int \limits _{-\infty }^{0}f(x)\;dx} и от нечётных функций: v.p.∫−∞∞f(x)dx=0{\displaystyle \mathrm {v.p.} \int \limits _{-\infty }^{\infty }f(x)\;dx=0} (v. p. обозначает главное значение несобственного интеграла по Коши).
    • Разложение в ряд Маклорена чётной функции содержит только члены с чётными степенями, а нечётной — только с нечётными.
    • Разложение в ряд Фурье периодической чётной функции содержит только члены с косинусами, а периодической нечётной — только с синусами.
    • Чётные функции образуют коммутативную алгебру над полем действительных чисел. Однако это неверно для нечётных функций, поскольку их множество незамкнуто относительно умножения (произведение двух нечётных функций является чётной функцией).

    Примеры

    Ниже везде x∈R.{\displaystyle x\in \mathbb {R} .}

    Нечётные функции

    • Возведение в степень с нечётным целым показателем: f(x)=x2k+1,{\displaystyle f(x)=x^{2k+1},} где k∈Z{\displaystyle k\in \mathbb {Z} } — произвольное целое число.
    • Сигнум: f(x)={  1,x>0  0,x=0−1,x<0{\displaystyle f(x)={\begin{cases}\ \ 1,&x>0\\\ \ 0,&x=0\\-1,&x<0\end{cases}}}
    • Кубический корень y=x3{\displaystyle y={\sqrt[{3}]{x}}} и вообще корень любой положительной нечётной степени y=x2k+1,k∈N.{\displaystyle y={\sqrt[{2k+1}]{x}},\quad k\in \mathbb {N} .}
    • Тригонометрические функции: синус f(x)=sin⁡x,{\displaystyle f(x)=\sin x,} тангенс f(x)=tg⁡x,{\displaystyle f(x)=\operatorname {tg} x,} котангенс f(x)=ctg⁡x,{\displaystyle f(x)=\operatorname {ctg} x,} косеканс f(x)=cosec⁡x.{\displaystyle f(x)=\operatorname {cosec} x.}
    • Обратные тригонометрические функции: арксинус f(x)=arcsin⁡x,{\displaystyle f(x)=\arcsin x,} арктангенс f(x)=arctg⁡x,{\displaystyle f(x)=\operatorname {arctg} x,} арксеканс f(x)=arcsec⁡x,{\displaystyle f(x)=\operatorname {arcsec} x,} арккосеканс f(x)=arccosec⁡x.{\displaystyle f(x)=\operatorname {arccosec} x.}
    • Гиперболические функции: гиперболический синус, гиперболический косеканс.
    • Обратные гиперболические функции: ареасинус, ареатангенс, ареакосеканс.
    • Специальные и обобщённые функции:

    Чётные функции

    Литература

    wikiredia.ru

    Нечётные и чётные функции - это... Что такое Нечётные и чётные функции?

    Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.

     — пример нечётной функции.  — пример чётной функции. ни чётная, ни нечётная.

    Другие определения:

    • Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
    • Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
    • Индифферентная функция[источник не указан 240 дней] — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории.

    Определения

    Определения вводятся для любой симметричной относительно нуля области определения , например, отрезка или интервала.

    • Функция называется чётной, если справедливо равенство
    • Функция называется нечётной, если справедливо равенство

    (или функцией общего вида).

    Свойства

    • График нечётной функции симметричен относительно начала координат .
    • График чётной функции симметричен относительно оси ординат .
    • Произвольная функция может быть единственным образом представлена в виде суммы нечётной и чётной функций:

    где

    • Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
    • Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
    • Функция, обратная чётной, чётна, а нечётной — нечётна.
    • Произведение двух функций одной чётности чётно.
    • Произведение двух функций разной чётности нечётно.
    • Композиция двух нечётных функций нечётна.
    • Композиция чётной функции с чётной/нечётной чётна.
    • Композиция любой функции с чётной чётна (но не наоборот!).
    • Производная чётной функции нечётна, а нечётной — чётна.
      • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
    • Производная чётного порядка имеет ту же чётность, что и первоначальная функция.

    Примеры

    Нечётные функции

    Чётные функции

    Вариации и обобщения

    dis.academic.ru

    Четность функции

    Четность и нечетность функции являются одним из основных ее свойств, и исследование функции на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.

    Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.

    Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:

    • -x (противоположная точка) также лежит в данной области определения,

    Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О , являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка - b тоже лежит в этой области. Из вышесказанного, таким образом, вытекает вывод: четная функция имеет симметричный по отношению к оси ординат (Oy) вид.

    Как на практике определить четность функции?

    Пусть функциональная зависимость задается с помощью формулы h(x)=11^x+11^(-x). Следуя алгоритму, вытекающему непосредственно из определения, исследуем прежде всего ее область определения. Очевидно, что она определена для всех значений аргумента, то есть первое условие выполнено.

    Следующим шагом подставим вместо аргумента (x) его противоположное значение (-x).Получаем :h(-x) = 11^(-x) + 11^x. Поскольку сложение удовлетворяет коммутативному (переместительному) закону, то очевидно, h(-x) = h(x) и заданная функциональная зависимость – четная.

    Проверим четность функции h(x)=11^x-11^(-x). Следуя тому же алгоритму, получаем, что h(-x) = 11^(-x) -11^x. Вынеся минус, в итоге, имеем h(-x)=-( 11^x-11^(-x))=- h(x). Следовательно, h(x) – нечетная.

    Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.

    Четные функции обладают рядом интересных свойств:

    • в результате сложения подобных функций получают четную;
    • в результате вычитания таких функций получают четную;
    • функция, обратная четной, также четная;
    • в результате умножения двух таких функций получают четную;
    • в результате умножения нечетной и четной функций получают нечетную;
    • в результате деления нечетной и четной функций получают нечетную;
    • производная такой функции – нечетная;
    • если возвести нечетную функцию в квадрат , получим четную.

    Четность функции можно использовать при решении уравнений.

    Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами. Один из них подлежит проверке.

    Это же свойство функции успешно применяют для решения нестандартных задач с параметром.

    Например, есть ли какое-либо значение параметра a, при котором уравнение 2x^6-x^4-ax^2=1 будет иметь три корня?

    Если учесть, что переменная входит в уравнение в четных степенях, то понятно, что замена х на – х заданное уравнение не изменит. Отсюда следует, что если некоторое число является его корнем, то им же является и противоположное число. Вывод очевиден: корни уравнения, отличные от нуля, входят в множество его решений «парами».

    Ясно, что само число 0 корнем уравнения не является, то есть число корней подобного уравнения может быть только четным и, естественно, ни при каком значении параметра оно не может иметь трех корней.

    А вот число корней уравнения 2^x+ 2^(-x)=ax^4+2x^2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.

    fb.ru