ГлавнаяРазноеДоказать что функция непрерывна

6.5. Непрерывность функции и точки разрыва. Краткая теория. Доказать что функция непрерывна


6.5. Непрерывность функции и точки разрыва. Краткая теория

1.Функцияназываетсянепрерывной в точкеx0, если она удовлетворяет следующим условиям: 1) определена в точкеx0; 2) имеет конечный предел прих→x0;

3) этот предел равен значению функции в этой точке: (6.1)

(первое определение).

2. Функцияназываетсянепрерывной в точкеx0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:(6.2)

(второе определение).

3. Если функцииинепрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.

4.Если функцияу=непрерывна в точкеu0=, а функцияu=непрерывна в точкеx0, то сложная функция у =непрерывна в точкеx0.

5.Функция называетсянепрерывнойна некотором промежутке, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны во всех точках, где они определены.

6.Если не выполнено определение непрерывности (6.1) или (6.2), то функция в точкеx0терпит разрыв, причем:

а) если хотя бы один из односторонних пределов или

бесконечен, то x0-точка разрыва второго рода;

б) если оба односторонних предела иконечны, но не равны между собой, тоx0— точка неустранимого разрыва первого рода;

в) если оба односторонних предела иконечны, равны между собой, но не равны, тоx0— точка устранимого разрыва первого рода.

6.168. Исследовать на непрерывность функции у =в точкех = 1. В случае разрыва установить его характер в точкех= 1:

а) ; б); в); г).

Решение: а) При х = 1 функция не определена, следовательно, функция в точке

х= 1 терпит разрыв (рис. 6.1):, т.е. конечный предел существует; следовательно,х= 1 — точка устранимого разрыва первого рода. (Доопределив функцию в точкех= 1, т.е. положив= 0, получим, что новая функция

будет уже непрерывна в точке х = 1 .)

6) При x= 1 функция не определена, следовательно, функция в точкеx= 1 терпит разрыв (рис. 6.2):

Так как односторонние пределы (достаточно было бы одного) бесконечны, то х= 1 – точка разрыва функции второго рода.

в) При х= 1 функция определена,(x-1) = 0,(x-1) = 0,у(1) = 1 - 1 = 0, т.е.у(х)=у(х) =у(1) = 0, следовательно, функция в точкех= 1 непрерывна

(рис. 6.3).

г) При х= 1 функция определена,у(1)=0,

у(х)=(х+1)=2,у(х)=(х-1)=0,

имеему(х) ≠у(х), таким образом, в точкех = 1 функция терпит неустранимый разрыв первого рода (рис. 6.4.)

Глава 7. Производная

7.1. Определение производной Краткая теория

1.Производной функции называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):

.(7.1)

Если функция в точке (или на промежутке) имеет конечную производную, то функция называетсядифференцируемойв этой точке (или на промежутке).

2.Если функция дифференцируема в точке ,(или на промежутке), то она в этой точке непрерывна (или на промежутке). Если функция непрерывна в данной точке, то она обязательно дифференцируема в данной точке.

1. Используя определение производной, найти производную функции.

Решение.Придавая аргументуприращение, найдем соответствующее приращение функции:

.

Составим отношение:

.

Найдем предел этого отношения при :

(ибо в силу (6.1) первый предел равен 1).

Таким образом: .

2.Доказать, что функциянепрерывна, но не дифференцируема в точке.

Решение. Функция:

  1. определена на всей числовой оси, в том числе в точке ;

  2. существует конечный предел ;

  3. этот предел равен значению функции в точке , т.е..

Таким образом, согласно определению (6.4) непрерывности функции в точке, функция непрерывна при .

Производная функции

,

т.е. функция не является дифференцируемой при .

Используя определение производной, найти производные функций:

1..

2..

3..

4..

5..

6..

Доказать, что функции непрерывны и дифференцируемы при :

7.,.

8.,.

Доказать, что функции являются непрерывными, но не дифференцируемы при :

9.,.

10.,.

studfiles.net

Непрерывность функции в точке и на промежутке. С примерами

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t, выраженная законом s = f(t), даёт пример непрерывной функции f(t). Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f(t). Непрерывна и линия, если её можно начертить, не отрывая карандаш от бумаги. Эта линия и является графиком непрерывной функции.

Графически функция непрерывна в точке , если её график не "разрывается" в этой точке. График такой непрерывной функции - показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:

Если хотя бы одно из этих условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 - на рисунке ниже.

Пример 1. Функция f(x) определена следующим образом:

Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0, x = 1, x = 3?

Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0. Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

.

Предел функции и значение функции в точке x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0.

Точка x = 1. Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1.

Точка x = 3. Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3.

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m, то есть l = f(m), m≥0.

Непрерывность функции на промежутке

Пусть функция y = f(x) определена в интервале ]a, b[ и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в интервале ]a, b[. Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b[, ]a, + ∞[, ]- ∞, + ∞[. Пусть теперь функция y = f(x) определена на отрезке [a, b]. Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a, оставаясь на отрезке [a, b], мы можем приближаться только справа, а к точке b - только слева. Функция называется непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b.

Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a, b], функция непрерывна на отрезке [0, b], функция непрерывна на любом отрезке, не содержащем точку a = 2.

Пример 2. Исследовать функцию на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках - 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах

.

Пример 3. Определить, при каком значении параметра a непрерывна на всей области определения функция

Решение. Найдём левосторонний предел функции в точке :

.

Найдём правосторонний предел при :

.

Очевидно, что значение в точке x = 2 должно быть равно ax:

Ответ: функция непрерывна на всей области определения при a = 1,5.

В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.

2. Функция f(x), непрерывная на интервале [a, b], принимает все промежуточные значения между значениями в концевых точках, то есть, между f(a) и f(b). В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.

3. Если функция непрерывна на интервале, то на этом интервале она достигает своего наибольшего и своего наименьшего значения: если m - наименьшее, а M - наибольшее значение функции на интервале [a, b], то найдутся на этом отрезке такие точки и , что и . Теорема, в которой изложено это свойство, называется второй теоремой Вейерштрасса.

Пример 5. Используя первое из приведённых выше свойств непрерывных функций, доказать, что уравнение имеет по меньшей мере один вещественный корень в интервале [1; 2].

Решение.

Пусть .

Вычислим значения функции при x = 1 и x = 2.

.

.

Получили, что функция на концах интервала принимает значения разных знаков: и , т. е.

Следовательно, в интервале [1; 2] существует такое число a, при котором f(a) = 0. То есть, уравнение имеет по меньшей мере один вещественный корень в данном интервале.

Установление непрерывности функции может быть как самостоятельной задачей, так и частью Полного исследования функции и построения графика.

Весь раздел "Исследование функций"

function-x.ru

Непрерывные функции (Лекция №4)

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

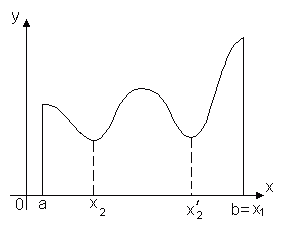
Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x1 Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x2'.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C.

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C.

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента xиз этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x0 и новое x.

Разность x– x0 называется приращением аргумента x в точке x0 и обозначается Δx. Таким образом, Δx = x – x0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x0+Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x0 значение функции было f(x0), то в новой точке x функция будет принимать значение f(x) = f(x0 +Δx).

Разность y – y0 = f(x) – f(x0) называется приращением функции y = f(x) в точке x0 и обозначается символом Δy. Таким образом,

Δy = f(x) – f(x0) = f(x0 +Δx) - f(x0). (1)

Обычно исходное значение аргумента x0 считается фиксированным, а новое значение x – переменным. Тогда y0 = f(x0) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δxтакже будут переменными и формула (1) показывает, что Dy является функцией переменной Δx.

Составим отношение приращения функции к приращению аргумента

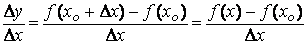
Найдем предел этого отношения при Δx→0. Если этот предел существует, то его называют производной данной функции f(x) в точке x0 и обозначают f '(x0). Итак,

.

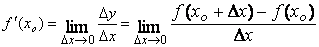Производной данной функции y = f(x) в точке x0 называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю.

Заметим, что для одной и той же функции производная в различных точках xможет принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)

Производная обозначается символами f '(x),y ', 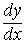. Конкретное значение производной при x = aобозначается f '(a) или y '|x=a.

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило:

  1. Придать x приращение Δx и найти наращенное значение функции f(x + Δx).
  2. Найти приращение функции Δy = f(x + Δx) – f(x).
  3. Составить отношение и найти предел этого отношения при Δx∞0.

Примеры.

  1. Найти производную функции y = x2

    а) в произвольной точке;

    б) в точке x= 2.

    а)

    1. f(x + Δx) = (x + Δx)2;
    2. Δy = (x + Δx)2 – x2=2xΔx– x2;
    3. .

      б) f '(2) = 4

  2. Используя определение найти производную функции в произвольной точке.
    1. .

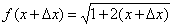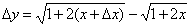
МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t0. К этому моменту точка прошла путь s=s(t0). Определим скорость vматериальной точки в момент времени t0.

Для этого рассмотрим какой-нибудь другой момент времени t0+Δt. Ему соответствует пройденный путь s=s(t0+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t0+Δt)–s(t).

Рассмотрим отношение 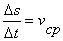. Оно называется средней скоростью в промежутке времени Δt. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt.

Итак, скоростью движения в данный момент времени t0 (мгновенной скоростью) называется предел средней скорости в промежутке от t0 до t0+Δt, когда Δt→0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

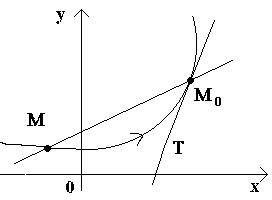
Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M0M. Если точка М начинает перемещаться по кривой, а точка М0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М0 с любой стороны секущая стремится занять положение определенной прямой М0Т, то прямая М0Т называется касательной к кривой в данной точке М0.

Т.о., касательной к кривой в данной точке М0 называется предельное положение секущей М0М, когда точка М стремится вдоль кривой к точке М0.

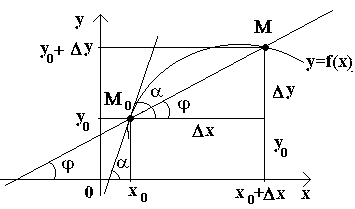
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х0 функция принимает значение y0=f(x0). Этим значениям x0 и y0 на кривой соответствует точка М0(x0; y0). Дадим аргументу x0 приращение Δх. Новому значению аргумента соответствует наращенное значение функции y0+Δ y=f(x0–Δx). Получаем точку М(x0+Δx; y0+Δy). Проведем секущую М0М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .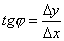

Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М0. Тогда секущая М0М будет стремиться занять положение касательной к кривой в точке М0, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

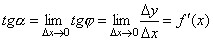
т.е. f '(x) = tg α .

Т.о., геометрически у '(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М0 (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х2 в точке М(-1; 1).

Ранее мы уже видели, что (x2)' = 2х. Но угловой коэффициент касательной к кривой есть tg α = y'|x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство. Если , то

,

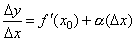где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

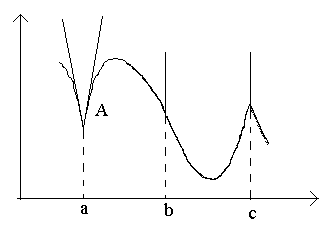
Рассмотрим на рисунке точки а, b, c.

В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.

В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной 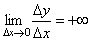. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.

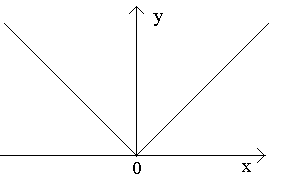
Примеры.

  1. Рассмотрим функцию y=|x|.Эта функция непрерывна в точке x = 0, т.к. .

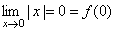    Покажем, что она не имеет производной в этой точке.

    f(0+Δx) = f(Δx) = |Δx|. Следовательно, Δy = f(Δx) – f(0) = |Δx|

    Но тогда при Δx< 0 (т.е. при Δx стремящемся к 0 слева)

    А при Δx > 0

    Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

  2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

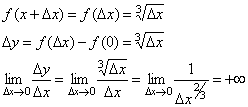
    Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

www.toehelp.ru

непрерывность-функции / Доказать, что $%f$% непрерывна в $%G$% / Математика

Отметим такой простой факт. Пусть расстояния от точек $%a$% и $%b$% числовой прямой до точки $%z_0$% меньше $%\varepsilon > 0$%. Тогда отрезок, соединяющий $%a$% и $%b$%, целиком содержится в $%\varepsilon$%-окрестности точки $%z_0$%. Поэтому для любой точки $%c$%, лежащей между $%a$% и $%b$%, её расстояние до $%z_0$% также будет меньше $%\varepsilon$%.

Пусть функция $%f$% непрерывна по каждой из переменных в отдельности и монотонна по $%x$%. Докажем, что она непрерывна в произвольной точке $%(x_0,y_0)$% как функция двух переменных. Рассмотрим $%\delta_1 > 0$% такое, что для всех $%x\in[x_0-\delta_1,x_0+\delta_1]$% выполняется неравенство $%|f(x,y_0)-f(x_0,y_0)| < \varepsilon/2$%. Теперь для каждой из точек $%x_0\pm\delta_1$% воспользуемся непрерывностью функции по $%y$% в этих точках, и выберем соответствующие окрестности по $%y$%, обозначая через $%\delta_2$% радиус меньшей из них. Получится, что при $%|y-y_0|\le\delta_2$% справедливы неравенства $%|f(x_0-\delta_1,y)-f(x_0-\delta_1,y_0)| < \varepsilon/2$%, а также $%|f(x_0+\delta_1,y)-f(x_0+\delta_1,y_0)| < \varepsilon/2$%.

Рассматривая прямоугольник $%[x_0-\delta_1,x_0+\delta_1]\times[y_0-\delta_2,y_0+\delta_2]$%, убеждаемся в том, что для любых точек вида $%(x,y)=(x_0\pm\delta_1,y)$% на его боковых сторонах справедливо неравенство $%|f(x,y)-f(x_0,y_0)| < \varepsilon$%, что следует из неравенства треугольника. Тогда, если $%(x,y)$% -- произвольная точка рассматриваемого прямоугольника, то значение $%f(x,y)$% находится между значениями функции $%f(x_0-\delta_1,y)$% и $%f(x_0-\delta_1,y)$% в точках на боковых сторонах. В силу сделанного в начале замечания, $%f(x,y)$% удалена от $%f(x_0,y_0)$% менее чем на $%\varepsilon$% для любой точки прямоугольника.

отвечен 21 Июн '15 15:54

math.hashcode.ru