ГлавнаяРазноеДроби как решать сложные

Как решать уравнения с дробями. Показательное решение уравнений с дробями. Дроби как решать сложные


Сложные выражения с дробями. Порядок действий

8 августа 2011

Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?

В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:

  1. Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
  2. Затем — деление и умножение;
  3. Последним шагом выполняется сложение и вычитание.

Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.

Задача. Найдите значения выражений:

Переведем все дроби из первого выражения в неправильные, а затем выполним действия:

Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2. Тогда:

Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3, имеем:

Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.

Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:

Многоэтажные дроби

До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.

Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:

Здесь и далее мы будем называть эти дроби многоэтажными. Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.

Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:

Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:

Задача. Переведите многоэтажные дроби в обычные:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:

В последнем примере перед окончательным умножением дроби были сокращены.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

Это выражение можно прочитать по-разному:

  1. В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
  2. В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.

Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

Задача. Найдите значения выражений:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

Смотрите также:

  1. Умножение и деление дробей
  2. Тест к уроку «Сложные выражения с дробями» (легкий)
  3. Тест к уроку «Округление с избытком и недостатком» (1 вариант)
  4. Площади многоугольников на координатной сетке
  5. Периодические десятичные дроби
  6. Задача B2: лекарство и таблетки

www.berdov.com

Сложные дробные выражения

Более сложным вариантом дробных выражений являются такие, в которых числитель и знаменатель являются числовыми выражениями.

Пример 1: Найти значение выражения $$\dfrac{1{,}2+\frac45}{2\frac58-0{,}7}$$.

Решение: Найдем отдельно значения выражений, стоящих в числителе и в знаменателе, а потом разделим первое на второе.

Числитель: $$$1{,}2+\frac45=1{,}2+0{,}8=2$$$ Знаменатель: $$$2\frac58-0{,}7=\dfrac{21}{8}^{\backslash 10}-\dfrac7{10}^{\backslash 8}=\dfrac{210}{80}-\dfrac{56}{80}=\dfrac{210-56}{80}=\dfrac{154}{80}=\dfrac{77}{40}$$$ Теперь разделим числитель на знаменатель: $$$\dfrac{2}{\frac{77}{40}}=2\cdot\dfrac{40}{77}=\dfrac{80}{77}$$$ Ответ: $$\dfrac{80}{77}$$

Пример 2: Найти значение выражения $$\dfrac{2{,}4\cdot 12{,}6\cdot3{,}5}{6{,}3\cdot3{,}6}$$.

Решение: В данном выражении числитель и знаменатель являются произведениями десятичных дробей. Для нахождения значения можно вычислить оба произведения, а потом разделить числитель на знаменатель. Но можно несколько упростить себе задачу, домножив на такой дополнительный множитель, чтобы десятичные дроби в числителе и знаменателе стали натуральными числами.

$$2{,}4$$ надо умножить на $$10$$, чтобы получить натуральное число $$2{,}4\cdot 10=24$$. $$12{,}6$$ надо умножить на $$10$$, чтобы получить натуральное число $$12{,}6\cdot 10=126$$. $$3{,}5$$ надо умножить на $$10$$, чтобы получить натуральное число $$3{,}5\cdot 10=35$$.

Значит, числитель надо умножить на $$10\cdot10\cdot10=1000$$, чтобы все множители стали натуральными. Но тогда и знаменатель надо умножить на это же число $$1000$$, иначе значение дроби изменится. Знаменатель в таком случае станет равен $$$6{,}3\cdot3{,}6\cdot(10\cdot10\cdot10)=(6{,}3\cdot10)\cdot(3{,}6\cdot10)\cdot10=63\cdot36\cdot10$$$ Итак, после домножения на дополнительный множитель $$1000$$ получаем: $$$\dfrac{2{,}4\cdot 12{,}6\cdot3{,}5}{6{,}3\cdot3{,}6}^{\backslash 1000}=\dfrac{24\cdot126\cdot35}{63\cdot36\cdot10}$$$ И теперь, перед тем как находить произведения в числителе и знаменателе, выполним предварительное сокращение: $$$\begin{align} &\phantom{=}\dfrac{24\cdot126\cdot35}{63\cdot36\cdot10}=&&\text{сократим 24 и 36 на 12}\\ \\ &=\dfrac{2\cdot126\cdot35}{63\cdot3\cdot10}=&&\text{сократим 126 и 63 на 63}\\ \\ &=\dfrac{2\cdot2\cdot35}{1\cdot3\cdot10}=&&\text{сократим 35 и 10 на 5}\\ \\ &=\dfrac{2\cdot2\cdot7}{3\cdot2}=\dfrac{2\cdot7}{3}=\dfrac{14}{3} \end{align}$$$ Ответ: $$\dfrac{14}{3}$$

Пример 3: Найти значение выражения $$\dfrac{(7-6{,}35):6{,}5+9{,}9}{\left(1{,}2:36+1{,}2:0{,}25-1\frac{5}{16}\right):\frac{169}{24}}$$.

Решение: Найдем отдельно значения выражений, стоящих в числителе и в знаменателе, а потом разделим первое на второе.

Числитель: $$\begin{align} &(7-6{,}35):6{,}5+9{,}9=&&\text{найдем разность в скобках}\\ \\ =&0{,}65:6{,}5+9{,}9=&&\text{преобразуем делимое и делитель в обыкновенные дроби}\\ \\ =&\dfrac{65}{100}:\dfrac{65}{10}+9{,}9=&&\text{заменим деление умножением на число, обратное делителю}\\ \\ =&\dfrac{65}{100}\cdot\dfrac{10}{65}+9{,}9=&&\text{сократим на 65 и на 10}\\ \\ =&\dfrac1{10}+9{,}9=0{,}1+9{,}9=10 \end{align}$$

Знаменатель:

$$\begin{align} &\left(1{,}2:36+1{,}2:0{,}25-1\frac{5}{16}\right):\frac{169}{24}=&&\text{преобразуем все дроби в обыкновенне}\\ \\ &=\left(\dfrac{12}{10}\cdot\dfrac1{36}+\dfrac{12}{10}\cdot\dfrac{100}{25}-\frac{21}{16}\right)\cdot\frac{24}{169}=&&\text{сократим первое произведение на 3, второе на 10 и 5}\\ \\ &=\left(\dfrac{1}{30}+\dfrac{24}{5}^{\backslash 6}-\frac{21}{16}\right)\cdot\frac{24}{169}=&&\text{приведем 1ю и 2ю дроби в скобках к общему знаменателю 30}\\ \\ &=\left(\dfrac{1}{30}+\dfrac{144}{30}-\frac{21}{16}\right)\cdot\frac{24}{169}=&&\text{сложим 1ю и 2ю дроби в скобках}\\ \\ &=\left(\dfrac{145}{30}-\frac{21}{16}\right)\cdot\frac{24}{169}=&&\text{сократим 1ю дробь в скобках на 5}\\ \\ &=\left(\dfrac{29}{6}^{\backslash 8}-\frac{21}{16}^{\backslash 3}\right)\cdot\frac{24}{169}=&&\text{приведем дроби в скобках к общему знаменателю 48}\\ \\ &=\left(\dfrac{232}{48}-\frac{63}{48}\right)\cdot\frac{24}{169}=&&\\ \\ &=\dfrac{232-63}{48}\cdot\dfrac{24}{169}=\dfrac{169}{48}\cdot\dfrac{24}{169}=\dfrac12 \end{align}$$

Теперь разделим числитель на знаменатель и найдем значение выражения: $$$\dfrac{10}{\frac12}=10\cdot\dfrac21=20$$$ Ответ: $$20$$

Дробные выражения, равные $$0$$ и дробные выражения не имеющие смысла

Если знаменатель дроби или дробного выражения равен $$0$$, то такая дробь или дробное вражение не имеет значения, так как на ноль делить нельзя. В таких случаях говорят, что дробь не имеет смысла.Пример 4: Убедимся, что дробное выражение $$\dfrac{9{,}7\cdot2\frac34-2\left( \dfrac{17}2:0{,}8+\dfrac89 \right)}{\left( 3{,}6-2\frac1{15} \right)\cdot 5-7\frac23}$$ не имеет смысла.

Решение: Дробь не имеет смысла, если её знаменатель равен $$0$$. Поэтому нам надо убедиться, что значение выражения, которое стоит в знаменателе данной дроби равно $$0$$. $$$\begin{align} &\left( 3{,}6-2\frac1{15} \right)\cdot 5-7\frac23=\left( \dfrac{36}{10}-\dfrac{31}{15} \right)\cdot 5-7\frac23=\\ \\ =&\left( \dfrac{108}{30}-\dfrac{62}{30} \right)\cdot 5-7\frac23=\dfrac{46}{30}\cdot5-7\frac23=\\ \\ =&\dfrac{46}{6}-7\frac23=\dfrac{23}3-7\frac23=7\frac23-7\frac23=0 \end{align}$$$ Как мы видим, знаменатель этого дробного выражения равен $$0$$, значит выражение не имеет смысла.

Ответ: дробное выражение не имеет смысла

Значение дроби или дробного выражения равно $$0$$, если эта дробь имеет смысл и её числитель равен $$0$$.Пример 5: Найти значение выражения $$\dfrac{\left( 1\frac29:7\frac13-\dfrac16 \right)\cdot 0{,}23}{2\frac16+1{,}7}$$.

Решение: Найдем отдельно значение числителя и знаменателя этого дробного выражения. Числитель: $$$\begin{align} &\left( 1\frac29:7\frac13-\dfrac16 \right)\cdot 0{,}23=\left( \dfrac{11}9:\dfrac{22}3-\dfrac16 \right)\cdot 0{,}23=\\ \\ =&\left( \dfrac{11}9\cdot\dfrac3{22}-\dfrac16 \right)\cdot 0{,}23=\left( \dfrac{11}9\cdot\dfrac3{22}-\dfrac16 \right)\cdot 0{,}23=\\ \\ =&\left( \dfrac16-\dfrac16 \right)\cdot 0{,}23=0\cdot0{,}23=0 \end{align}$$$ Знаменатель: $$$2\frac16+1{,}7=\dfrac{13}6+\dfrac{17}{10}=\dfrac{65}{30}+\dfrac{51}{30}=\dfrac{116}{30}$$$ Мы выяснили, что знаменатель этой дроби не равен нулю, то есть она имеет смысл, а числитель равен нулю. Значит, значение этого дробного выражения равно $$0$$.

Ответ: $$0$$

Пример 6: Найти значение выражения $$\dfrac{3{,}6:1\frac{11}{25}-2{,}5}{\dfrac59\cdot\left( \dfrac13-0{,}8\cdot \dfrac16 \right)-\dfrac19}$$.

Решение: Найдем отдельно значение числителя и знаменателя этого дробного выражения.

Числитель: $$$3{,}6:1\frac{11}{25}-2{,}5=\dfrac{36}{10}:\dfrac{36}{25}-2{,}5=\dfrac{36}{10}\cdot\dfrac{25}{36}-2{,}5=\dfrac{25}{10}-2{,}5=2{,}5-2{,}5=0$$$ Знаменатель: $$$\begin{align} &\dfrac59\cdot\left( \dfrac13-0{,}8\cdot \dfrac16 \right)-\dfrac19=\dfrac59\cdot\left( \dfrac13-\dfrac8{10}\cdot \dfrac16 \right)-\dfrac19=\\ =&\dfrac59\cdot\left( \dfrac{10}{30}-\dfrac4{30} \right)-\dfrac19=\dfrac59\cdot\dfrac6{30}-\dfrac19=\dfrac19-\dfrac19=0 \end{align}$$$ Числитель данного дробного выражения равен $$0$$, но и его знаменатель тоже равен $$0$$. Значит, данное выражение не имеет смысла.

Ответ: не имеет значения

lomonosovclass.com

Как складывать дроби с разными знаменателями

Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.

Чтобы сложить или вычесть дроби с разными знаменателями, надо:

1) Найти наименьший общий знаменатель (НОЗ) данных дробей.

2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.

3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.

4) Проверить, является ли полученная в результате дробь правильной и несократимой.

В следующих примерах надо сложить или вычесть дроби с разными знаменателями:

   

   

Решение:

   

1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится. Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.

2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.

3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.

4) Полученная дробь — правильная и несократимая. Значит, это — ответ.

   

1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.

2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.

3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.

4)Полученная в результате дробь — правильная и несократимая.

   

1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.

2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.

3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.

4) полученную дробь надо сократить на 5.

   

1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.

2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.

3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.

www.for6cl.uznateshe.ru

Как решать уравнения с дробями. Показательное решение уравнений с дробями.

Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.Например, требуется решить простое уравнение x/b + c = d.

Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.

Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.

Например, как решить дробное уравнение:x/5+4=9Умножаем обе части на 5. Получаем:х+20=45 x=45-20=25

Другой пример, когда неизвестное находится в знаменателе:

b/x + c = d

Уравнения такого типа называются дробно-рациональными или просто дробными.

Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:

Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.

Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.

Например, требуется решить дробное уравнение:

1/x + 2 = 5

Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.

Избавляемся от знаменателя путем умножения всех членов уравнения на х

1 + 2x = 5х

И решаем обычное уравнение

5x – 2х = 13x = 1х = 1/3

Ответ: х = 1/3

Решим уравнение посложнее:

Здесь также присутствует ОДЗ: х -2.

Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.

Для сокращения знаменателей требуется левую часть умножить на х+2, а правую - на 2. Значит, обе части уравнения надо умножать на 2(х+2):

Это самое обычное умножение дробей, которое мы уже рассмотрели выше

Запишем это же уравнение, но несколько по-другому

Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:

4 = х + 2

х = 4 – 2 = 2, что соответствует нашей ОДЗ

Ответ: х = 2.

Для закрепления материала рекомендуем еще посмотреть видео.

Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

Как научиться решать дроби? - Полезная информация для всех

  • Сама столкнулась с тем, что дроби оказались достаточно сложной темой для моих детей.

    Есть очень хорошая игра quot;Дроби Никитинаquot;, она предназначена для дошкольников, но и в школе отлично поможет ребенку разобраться , что же все-таки это такое - дроби, их соотношение друг к другу..., причем все в доступной, наглядной и увлекательной форме.

    Представляет она из себя двенадцать разноцветных кругов. Один круг - целый, а все остальные поделены на равные части - две, три.... ( до двенадцати).

    Ребнку предлагается выполнить несложные игровые задания, например:

    Как называютсячасти кружков? или

    Какая часть больше? ( наложить меньшую на большую.)

    Моим эта методика помогла. Вообще очень жалею , что все эти quot; Никитинские развивашкиquot; не попались на глаза, когда дети были еще малышами.

    Игру можно сделать самостоятельно или купить готовую, а узнать обо всем подробней - здесь.

  • Решение дробей можно объяснить и на кубиках Lego. Он развивает не только воображение, но и творческое и логическое мышление, а значит, его можно использовать и как учебное пособие.

    Алишия Зиммерман придумала использовать кубики известного конструктора для обучения детей основам математики.

    И вот как на основе конструктора Lego можно объяснить дроби.

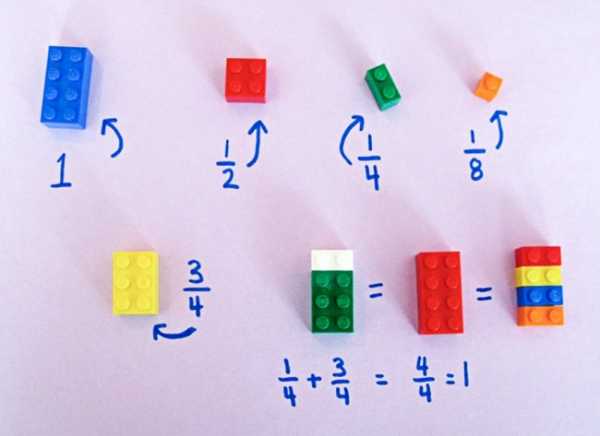
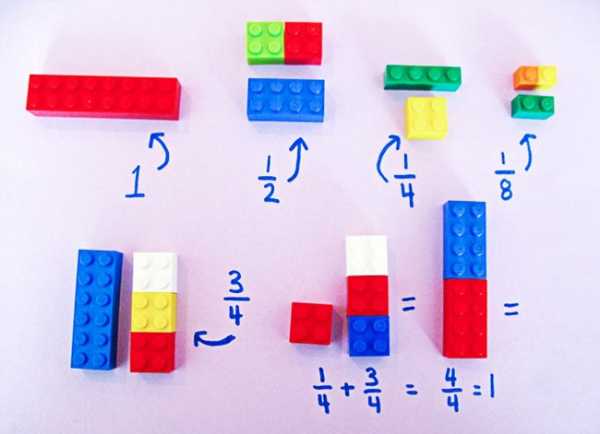
  • Практика показывает, что больше всего трудностей возникает при сложении (вычитании) дробей с разными знаменателями и при делении дробей.

    Трудности возникают из-за кривых указаний в учебнике, как, например, разделить дробь на дробь.

    quot;Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а числитель второй дроби на знаменатель первой дробиquot;.

    Может ли ребенок в 4 классе это понять и не запутаться? НЕТ!

    А нам учительница объяснила элементарно: нужно вторую дробь перевернуть, а потом умножить!

    Тоже самое со сложением.

    quot;Чтобы сложить две дроби, нужно числитель первой дроби умножить на знаменатель второй дроби, а числитель второй дроби умножить на знаменатель первой дроби, полученные числа сложить и записать в числитель. А в знаменатель нужно записать произведение знаменателей дробей. После этого полученную дробь можно (или нужно) сократитьquot;.

    А проще так: quot;Приведите дроби к общему знаменателю, который равен НОК знаменателей, а потом сложите числителиquot;.

  • Показать им на наглядном примере. Например, яблоко разрежьте на 4 части, на 8, на 12 сложите в целое, сложите несколько частей, отнимите. При этом на бумаге объясняйте с использованием правил. Правила сложения, вычитания. деления дробей, а так же как из неправильной дроби выделить целое - вс это учите в ходе манипуляций с яблоком. Не торопите детей, пусть внимательно с вашей помощью разберутся с дольками.

  • Научить решать дроби, в частности детей, это дело вполне обычно и не создаст много хлопот. Самое просто что можно сделать, это взять что-то целое, например мандарин, или любой другой плод, разделить его не части, и на примере показывать вычитания, сложение и другие операции с кусочками этого плода, что и будет дробями от целого. Все нужно объяснять и показывать, и завершающим фактором будет на математических примерах объяснять и решать задания совместно, пока ребенок сам не научиться делать эти задания.

    На рисунке наглядно видно что чему соответствует и как смотрится дробь на реальном предмете, именно так и нужно объяснять.

  • Вам к этому вопросу, нужно подойти основательно, так как решение дробей в жизни пригодится. Нужно в этом вопросе, как говорится, с детьми быть на равных, и объяснять теорию на им доступном языке, например на языке quot;тортаquot; или мандарина. Нужно делить торт на до и раздавать друзьям, после чего ребенок начнет вникать в суть решения дробей. Не начинайте с тяжелых дробей, начните с понятий 1/2, 1/3, 1/10. Сначала отнимайте и прибавляйте, а потом переходите на более сложные понятия как умножение и деление.

  • Проблемы с дробями бывают разные. Один ребнок не может понять, что одна вторая и пять десятых - это одно и то же, у других вызывает недоумение приведение различных дробей к одному знаменателю, у третьих - деление дробей. Поэтому и одного правила на все случаи жизни нет.

    Главное в задачах на дроби - не упустить момент, когда понятное перестат таковым быть. Возвращаться к quot;печкеquot; и повторять вс сначала, даже если оно кажется убого-примитивным. Например, вернуться к тому, что такое одна вторая.

    Ребнок должен понять, что математические понятия - абстрактны, что одно и то же явление можно описать разными словами, выразить разными числами.

  • Мне нравится ответ, данный Mefody66. Добавлю из личной многолетней практики: научить решать задачи с дробями (а не решать дроби; решать дроби нельзя, равно как невозможно решать числа) довольно несложно, надо лишь быть рядом с ребенком, когда он только приступает к решению таких задач, вовремя корректировать его решение, дабы ошибки, которые неизбежны при любом обучении, не успели закрепиться в сознании ребенка. Переучивать сложнее, чем учить новое. И как можно больше решать таких задач. Довести до автоматизма решение таких заданий - вот это хорошо бы сделать. Умение решать задачи с обыкновенными дробями по важности в школьном курсе математики занимает такое же место, как и знание таблицы умножения. Так что надо не полениться и проследить, как ваш ребенок решает такие задачи.

    И не очень опирайтесь при этом на учебник: учителя в школах объясняют именно так, как писал в своем ответе Mefody66. Лучше поговорить с учителем, выяснить, какими словами учитель объяснял эту тему. И использовать по возможности те же слова и фразы (чтобы не сильно запутывать ребенка)

    Еще: наглядные примеры использовать советую лишь на начальном этапе объяснения, потом побыстрее абстрагироваться, переходить к алгоритму решения. Иначе наглядность может повредить при решении более сложных задач. Например, если надо сложить дроби со знаменателями 29 и 121 - какая тут наглядность поможет? Только запутает.

  • Дроби - одна из тех благодатных математических тем, где нет не приложимых к делу абстракций. В ход идти должны продукты ( на quot;тортахquot; , как Хуаните Солис в quot;Отчаянных домохозяйкахquot; - реально классный метод объяснений). Все эти числители-знаменатели - потом. Потом нужно, чтобы ребенок понял, что деление на дробь уже и не уменьшение вовсе, а умножение- не прибавка. Тут лучше показать, как делить на дробь в форме умножения на перевертыш. В игровой форме подать сокращение, если делятся на одно число, то делить, почти судоку получается, если заинтересовать. Главное вовремя заметить непонятки, потому что дальше будут темы покруче, которые понять не просто. Поэтому побольше практики решении дробей и все быстро наладится. Мне, гуманитарию наичистейшему, далкому от малейшей степени абстракции, дроби всегда были понятны, чем остальные темы.

    • info-4all.ru

    Дроби, операции с дробями | umath.ru

    Дробь — форма представления числа в математике. Дробная черта обозначает операцию деления. Числителем дроби называется делимое, а знаменателем — делитель. Например, в дроби числителем является число 5, а знаменателем — 7.

    Правильной называется дробь, у которой модуль числителя больше модуля знаменателя. Если дробь является правильной, то модуль её значения всегда меньше 1. Все остальные дроби являются неправильными.

    Дробь называют смешанной, если она записана как целое число и дробь. Это то же самое, что и сумма этого числа и дроби:

       

    Основное свойство дроби

    Если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится, то есть, например,

       

    Приведение дробей к общему знаменателю

    Чтобы привести две дроби к общему знаменателю, нужно:

    1. Числитель первой дроби умножить на знаменатель второй
    2. Числитель второй дроби умножить на знаменатель первой
    3. Знаменатели обеих дробей заменить на их произведение

    Действия с дробями

    Сложение. Чтобы сложить две дроби, нужно

    1. Привести дроби к общему знаменателю
    2. Сложить новые числители обеих дробей, а знаменатель оставить без изменений

    Пример:

       

    Вычитание. Чтобы вычесть одну дробь из другой, нужно

    1. Привести дроби к общему знаменателю
    2. Вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений

    Пример:

       

    Умножение. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели:

       

    Деление. Чтобы разделить одну дробь на другую, следует числитель первой дроби умножить на знаменатель второй, а знаменатель первой дроби умножить на числитель второй:

       

    umath.ru

    Вычитание дробей с разными знаменателями. Сложение и вычитание обыкновенных дробей

    Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить абстрактное мышление и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» - сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.

    Как вычесть дроби, знаменатели которых одинаковые

    Дроби – это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:

    Примеры вычитания дробей, знаменатели которых одинаковы

    Рассмотрим, как это выглядит на примере:

    7/19 - 3/19 = (7 - 3)/19 = 4/19.

    От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби – «19».

    На картинке ниже приведено еще несколько подобных примеров.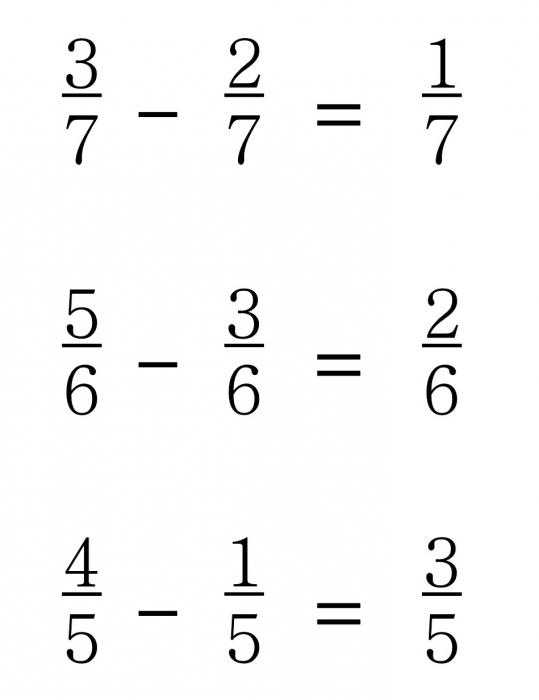

    Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:

    29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7)/47 = 9/47.

    От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей – «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, - «47».

    Сложение дробей, имеющих одинаковый знаменатель

    Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.

    Рассмотрим, как это выглядит на примере:

    1/4 + 2/4 = 3/4.

    К числителю первой слагаемой дроби - «1» - добавляем числитель второй слагаемой дроби - «2». Результат - «3» - записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, - «4».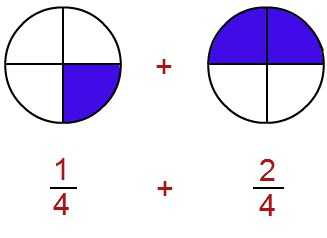

    Дроби с различными знаменателями и их вычитание

    Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.

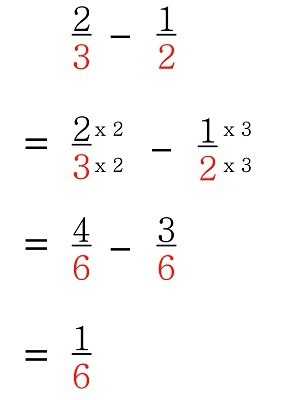
    О том, как это сделать, мы поговорим подробнее.

    Свойство дроби

    Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.

    Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:

    2/3 = 4/6 = 6/9 = 8/12…

    Как привести несколько дробей к одному и тому же знаменателю

    Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.

    Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.

    Рассмотрим первую дробь - 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.

    Аналогично производим действия с оставшимися дробями.

    Все вместе это выглядит так:

    Как вычесть и сложить дроби, имеющие различные знаменатели

    Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.

    Рассмотрим это на примере: 4/18 – 3/15.

    Находим кратное чисел 18 и 15:

    После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.

    Следующий этап нашего решения – приведение каждой дроби к знаменателю «90».

    Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:

    (4 х 5)/(18 х 5) – (3 х 6)/(15 х 6) = 20/90 – 18/90 = 2/90 = 1/45.

    Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.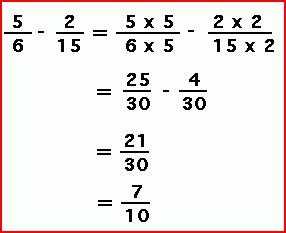

    Аналогично производится и сложение дробей, имеющих различные знаменатели.

    Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:

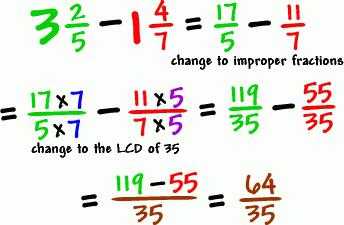
    Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.

    Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.

    Вычитание дробей из целого числа

    Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от натурального числа. На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:

    7 - 4/9 = (7 х 9)/9 - 4/9 = 53/9 - 4/9 = 49/9.

    Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.

    fb.ru