ГлавнаяРазноеЕсли известен класс точности что это означает

2.5.1 Классы точности средств измерений. Если известен класс точности что это означает


Что означает класс точности измерительного прибора

Класс точности измерительного прибора — это обобщенная черта, определяемая пределами допускаемых главных и дополнительных погрешностей, также другими качествами, влияющими на точность, значения которых установлены в эталонах на отдельные виды средств измерений. Класс точности средств измерений охарактеризовывает их характеристики в отношении точности, но не является конкретным показателем точности измерений, выполняемых с помощью этих средств.

Для того чтоб заблаговременно оценить погрешность, которую занесет данное средство измерений в итог, пользуются нормированными значениями погрешности. Под ними понимают предельные для данного типа средства измерений погрешности.

Погрешности отдельных измерительных устройств данного типа могут быть разными, иметь отличающиеся друг от друга периодические и случайные составляющие, но в целом погрешность данного измерительного прибора не должна превосходить нормированного значения. Границы основной погрешности и коэффициентов воздействия вносят в паспорт каждого измерительного прибора.

Главные методы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.

На шкале измерительного прибора маркируют значение класса точности измерительного прибора в виде числа, указывающего нормированное значение погрешности. Выраженное в процентах, оно может иметь значения 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 и т. д.

Если обозначаемое на шкале значение класса точности обведено кружком, к примеру 1,5, это значит, что погрешность чувствительностиδs=1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, измерительных шунтов, измерительных трансформаторов тока и напряжения и т. п.).

Это значит, что для данного измерительного прибора погрешность чувствительности δs=dx/x — неизменная величина при любом значении х. Граница относительной погрешности δ(х) постоянна и при любом значении х просто равна значению δs, а абсолютная погрешность результата измерений определяется как dx=δsx

Для таких измерительных устройств всегда указывают границы рабочего спектра, в каких такая оценка справедлива.

Если на шкале измерительного прибора цифра класса точности не подчеркнута, к примеру 0,5, это значит, что прибор нормируется приведенной погрешностью нуля δо=0,5 %. У таких устройств для всех значений х граница абсолютной погрешности нуля dx=dо=const, а δо=dо/хн.

При равномерной либо степенной шкале измерительного прибора и нулевой отметке на краю шкалы либо вне ее за хн принимают верхний предел спектра измерений. Если нулевая отметка находится посредине шкалы, то хн равно протяженности спектра измерений, к примеру для миллиамперметра со шкалой от -3 до +3 мА, хн= 3 — (-3)=6 А.

Но будет наигрубейшей ошибкой считать, что амперметр класса точности 0,5 обеспечивает во всем спектре измерений погрешность результатов измерений ±0,5 %. Значение погрешности δо возрастает назад пропорционально х, другими словами относительная погрешность δ(х) равна классу точности измерительного прибора только на последней отметке шкалы (при х = хк). При х = 0,1хк она в 10 раз больше класса точности. При приближении х к нулю δ(х) стремится к бесконечности, другими словами такими устройствами делать измерения в исходной части шкалы неприемлимо.

На измерительных устройствах с резко неравномерной шкалой (к примеру на омметрах) класс точности указывают в толиках от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».

Если обозначение класса точности на шкале измерительного прибора дано в виде дроби (к примеру 0,02/0,01), это показывает на то, что приведенная погрешность в конце спектра измерений δпрк = ±0,02 %, а в нуле спектра δпрк = -0,01 %. К таким измерительным устройствам относятся высокоточные цифровые вольтметры, потенциометры неизменного тока и другие высокоточные приборы. В данном случае

δ(х) = δк + δн (хк/х — 1),

где хк — верхний предел измерений (конечное значение шкалы прибора), х — измеряемое значение.

elektrica.info

Что такое класс точности прибора? :: SYL.ru

Класс точности – это характеристика прибора, которая определяется границами допускаемых основной и дополнительной погрешностей, а также другими свойствами, предусмотренными стандартами на данный вид изделия, которые оказывают влияние на точность. Этот параметр присутствует в технических характеристиках многих приборов, которые имеют эталонные выходные параметры, будь то электронные или механические измерительные устройства. Класс точности является основной характеристикой измерительной техники: весов, мультиметров, осциллографов, КИПовского оборудования и прочего. Чем выше это значение у прибора, тем больше стоит такое устройство, это связано со сложностью производства таких изделий.

Нормированная погрешность

Класс точности приборов измерений характеризует свойства таких изделий по отношению к точности, но при этом не является показателем точности этих измерений, выполненных при помощи данного устройства. С целью преждевременного выявления погрешности прибора, которую данное средство внесет в измеряемый результат, используют нормированные значения погрешностей. Значение этого параметра у каждого технического приспособления одной группы является индивидуальным, оно имеет отличные друг от друга случайные и систематические составляющие, но такая погрешность любого измерительного прибора одного класса не должна превышать установленное нормированное значение. Границы главной погрешности и коэффициента влияния заносятся в паспорт любого измерительного прибора. Все основные методы нормирования допустимых погрешностей и обозначения класса измеряющих устройств установлены ГОСТом, например, класс точности весов предусмотрен ГОСТом 24104-2001, который вступил в силу 01.07.2002.

Виды маркирования

Класс точности любого измерительного прибора маркируется на шкале устройства в виде числа. Это значение указывает нормированную величину погрешности, выраженную в процентном отношении. Если класс точности на шкале прибора обведен кружком, например 2,5, то это значит, что величина погрешности чувствительности устройства составляет 2,5 процента. По такому принципу нормируют погрешность масштабных преобразователей (измерительных шунтов, делителей напряжения, измерителей трансформаторов напряжения и тока и т. п.). Если значение класса точности на шкале прибора не подчеркнуто, например 0,7, это значит, что устройство нормируется погрешностью нуля равным 0,7. Эти приборы при любых з

начениях Х имеют абсолютную погрешность нуля, равную константе. В случае степенной или равномерной отметки класса точности на шкале устройства принимается верхний предел измерения. В том случае, когда нулевая отметка расположена по центру шкалы, то это значение принимается равным протяженности измеряемого диапазона. При этом будет неправильным считать, что амперметр с классом точности 0,7 обеспечит во всем измеряемом диапазоне погрешность результата 0,7%. В таком случае относительная погрешность будет равна классу точности только на последнем значении шкалы. На приборах с неравномерной шкалой (омметры) класс точности маркируют в долях от длины шкалы, его обозначают ниже значения знака «угол». В случае если класс точности указан в дробном виде (например, 0,03/0,02), это значит, что погрешность в конце измеряемого диапазона составит 0,03, а в начале 0,01. Такими приборами являются постоянные потенциометры, цифровые вольтметры и другие высокоточные измерительные приборы.

www.syl.ru

Класс точности - это... Что такое Класс точности?

Класс точности — основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.

Погрешность может нормироваться, в частности, по отношению к:

в этом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) заключается в кружок.

Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0 — 30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.

Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.

Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

Следует иметь в виду, что понятие класса точности встречается в различных областях техники. Так в станкостроении имеется понятие класса точности металлорежущего станка, класса точности электроэрозионных станков (по ГОСТ 20551).

Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.

Аппараты с классом точности 0,5 (0,2) начинают работать в классе от 5 % загрузки. а 0,5s (0,2s) уже с 1 % загрузки

См. также

Ссылки

dic.academic.ru

Konspekt_KSR_1_klassy_tochnosti

Конспект КСР1 (п. 8)

КЛАССЫ ТОЧНОСТИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

Класс точности измерительного прибора — это характеристика, определяемая нормированными предельными значениями погрешности средства измерений.

Способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ 8.401-80.

Способы нормирования допускаемых погрешностей:

- по абсолютной погрешности,

- по относительной погрешности,

- по приведенной погрешности – по длине или верхнему пределу шкалы прибора.

Обозначения классов точности измерительных приборов:

- арабскими цифрами без условных знаков - класс точности определяется пределами приведённой погрешности, в качестве нормирующего значения используется наибольший по модулю из пределов измерений.

- арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы.

По приведенной погрешности приборы делятся на классы: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Приборы класса точности 0,05; 0,1; 0,2; 0,5 применяются для точных лабораторных измерений и называются прецизионными.

В технике применяются приборы классов 1,0; 1,5: 2,5 и 4,0 (технические). 

Если на шкале такого обозначения нет, то данный прибор внеклассный, то есть его приведенная погрешность превышает 4%.

- арабскими цифрами в кружке - класс точности определяется пределами относительной погрешности.

- латинскими буквами, то класс точности определяется пределами абсолютной погрешности.

Когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления. При считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

Пример: вольтметр, диапазон измерений 0 — 30 В, класс точности 1,0 определяет, указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.

Относительная погрешность результата зависит от значения напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.

studfiles.net

2.5.1 Классы точности средств измерений

При высокоточных лабораторных измерениях предполагается строгое нормирование метрологических характеристик средства измерений (диапазон измерений, предел измерения, цена деления шкалы, чувствительность и др.). Основная метрологическая характеристика СИ – погрешность СИ – есть разность между показаниями СИ и истинными (действительными) значениями ФВ. Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные .

При технических измерениях, когда не предусмотрено выделение случайных и систематических составляющих, когда не существенна динамическая погрешность СИ, когда не учитываются влияющие (дестабилизирующие) факторы и т.д., можно пользоваться более грубым нормированием – присвоением СИ определенного класса точности по ГОСТ 8.401-80.

Класс точности — это обобщенная метрологическая характеристика СИ, определяемая предельными значениями допустимых основной и дополнительной погрешностей в рабочих диапазонах влияющих величин. Например, для основного параметра окружающей среды — температуры — в паспорте на прибор может быть записано: «......диапазон рабочих температур:0....+400С, диапазон температур хранения: -10...+600С». Класс точности СИ уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерений, выполняемых с помощью этих СИ, поскольку точность измерения зависит как от метода измерения, так и условий измерения. В частности, чтобы измерить величину с точностью до 1%, выбранное СИ должно обладать гораздо меньшей погрешностью. Для гарантированной заданной или расчетной погрешности измерений δиз относительная погрешность СИ δСИ должна быть на 25%-30% ниже чем δи (т.е. δси=0,7 δиз). Определяя класс точности, нормируют, прежде всего пределы допустимой основной погрешности δосн. Пределы допускаемой дополнительной погрешности устанавливают в виде дольного (кратного) значения ( δосн). Пределы допускаемых основной и дополнительной погрешностей выражают в форме абсолютной (), относительной (δ) или приведенной () погрешностей.

Приведенной погрешностью СИ (прибора) называют относительную погрешность, определяемую по формуле:

где — предельно допустимая (максимальная) абсолютная погрешность СИ, а Хн — нормирующее значение (чаще всего в качестве Хн выбирается верхний или конечный предел диапазона измерения прибора Хк).

ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования» в качестве основных устанавливает три вида классов точности СИ:

1) для пределов допускаемой абсолютной основной погрешности в единицах измеряемой величины или делениях шкалы;

2) для пределов допускаемой относительной погрешности в виде ряда чисел

где А=1; 1,5; 2; 2,5; 4; 5; n= 1; 0; -1; -2; -3......

3) для пределов допускаемой приведенной погрешности с тем же рядом чисел γ=±А10n. Например для класса точности 0,05 , А=5, n= -2. При этом проценты в обозначении класса точности не указываются;

Абсолютная погрешность может выражаться одним числом =а при аддитивном характере погрешности (ширина коридора значений не изменяется во всем измеряемом диапазоне значении Х, см. рисунок 2а), или двучленом Δ=(а+bх) при совместном проявлении аддитивной и мультипликативной составляющих, либо в виде таблицы (графика функции) при нелинейном изменении границ абсолютной погрешности (например, табл.1).

Таблица 1

Пределы допускаемой абсолютной погрешности вольтметра М-366

Показания СИ, В

0

10

20

30

40

50

60

70

75

Погрешность Δ, В

-0,2

-0,1

0

0,1

0,2

0,35

0,45

0,55

0,7

Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита тем больше значения допускаемой абсолютной погрешности. Буквенное обозначение принято для мер с аддитивной погрешностью, цифра ΙΙΙ для мер с обоими составляющими погрешности (см. табл.2).

Класс точности через относительную погрешность СИ назначается двумя способами:

- Если погрешность СИ имеет в основном мультипликативный характер (при этом относительная погрешность остается постоянной величиной g во всем измеряемом диапазоне), то пределы допускаемой основной относительной погрешности устанавливают по формуле [4 с.140.]

(2)

Так определяют классы точности мостов переменного тока, счетчиков электроэнергии, делителей напряжения, измерительных трансформаторов и др. При этом класс точности на СИ обозначается цифрой в кружке. Например .

- Если СИ имеют обе составляющих погрешности, то класс точности обозначается двумя цифрами c/d , соответствующими значениям с и d формулы

(3)

Здесь c и d выражаются также через ряд (1). Причем c>d, Хк — конечное значение шкалы, X – значение отсчета. Например, класс точности 0,02/0,01 означает, что с=0,02; а d=0,01.

Для некоторых СИ характерна сложная зависимость относительной погрешности от измеряемой величины или влияющих факторов, которая приводит к логарифмической характеристике точности. В основном это широкополосные СИ, например мосты постоянного тока, мосты сопротивлений, цифровые частомеры и т.д. Для них ГОСТ 8.401-80 допускает нормирование класса точности трехчленной формулой [4 c. 143]

δ(x)=(xmin/x+ δ3+x/xk)

(4)

где Хmin и Хк — порог и предел чувствительности, δз — относительная погрешность, ограничивающая снизу рабочий диапазон. При δз =0,5%, Хmin=0,02 Ом и Хк =20*106 Ом для любого Х относительная погрешность составит:

δx=(0,02/x+0,5/100+x/20∙10^6)100%.

(5)

Для приборов с существенно неравномерной шкалой нормирующее значение устанавливается равным длине шкалы или ее части, соответствующей диапазону измерений. В этом случае предел абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на шкалу прибора наносится обозначение класса точности в виде цифры под которой находится знак .Например, обозначение класса точности означает, что для данного прибора установлен предел допускаемой погрешности, составляющей 2,5% от длины шкалы, действительное значение измеряемой величины должно находиться в пределах ±2,5% от длины шкалы, отсчитанных от установившегося положения стрелки.

Обозначения классов точности в документах и на приборах приведены в табл. 2.

Таблица 2

Необходимо подчеркнуть, что класс точности является обобщенной характеристикой СИ данного типа. Значение его позволяет не определить погрешность конкретного измерения, а лишь указать пределы, в которых находится погрешность при измерении физической величины данным средством.

Пример. Отсчет по шкале прибора с приделами измерений 0-50А и равномерной шкалой составил 25А.Пренебрегаю другими видами погрешностей измерений, оценить пределы абсолютной погрешности этого отсчета при использовании амперметров с классами точности 0,02/0,01 , , 0,5. Выбрать амперметр, который бы давал погрешность отсчета, не превышающую 0,01А.

1.Для СИ класс точности 0,02/0,01 из табл.2 находим

,

2.Для СИ класс точности

% ,

3.Для СИ класс точности 0,5

,

Вывод. Погрешность отсчета не превышающую 0,01А обеспечит амперметр класса точности 0,02/0,01, а при использовании амперметра класса точности 0,5 погрешность отсчета будет превышать требуемую в 25 раз.

studfiles.net

Где и когда необходим класс точности

Точность измерительных приборов, а точнее, ее величина, имеет немаловажное значение, особенно когда речь идет о необходимости проведения измерения минимальных колебаний или взвешивании очень малых весов. Высокоточные приборы нужны при взвешивании химических веществ или драгоценных металлов, при замере показаний электрического напряжения, концентрации примесей в растворах или газах, фиксации колебаний давления или температуры.

Все измерительные приборы, неважно, являются они механическими или электрическими, вне зависимости от принципа их действия, подразделяются на несколько категорий. Главной метрологической характеристикой устройств и приборов для проведения измерений различного рода является класс точности, который определяет максимальную погрешность, допустимую при проведении измерений. Стоит отметить, что класс точности показывает лишь вероятные отклонения прибора от собственной шкалы, однако свидетельствовать о точности измерений, произведенных с помощью устройства, не может.

В зависимости от типа прибора, определяется его класс точности. Рассмотрим это на примерах. Так, у приборов со стрелочной шкалой класс точности будет обозначен цифрой, которая будет отображать величину погрешности при проведении измерений. В этом случае цифра 2,0 в обозначении класса скажет специалисту, что погрешность равна 2% от величины его шкалы.

Цифра, заключенная в кружок, будет говорить о том, что данная величина погрешности является константой для любой величины на шкале прибора. Погрешность в виде дроби будет означать величину неточности измерения в максимальном и минимальном измерении. Класс точности может быть обозначен цифрой (арабской или римской), буквой или цифрой с присоединением определенного символа или буквы. Так, например, класс точности весов будет обозначен цифрой и буквой. Например, 0а или 2б.

Класс точности приборов обязательно указывается шкале. Отсутствие подобного обозначения также имеет определенную смысловую нагрузку. Отсутствие показаний погрешности, которые могут быть получены в результате измерений, говорит о том, что данная цифра у конкретного прибора превышает 4%, он считается внеклассным. Для высокоточных измерений, необходимых, например, в лабораторных исследованиях, применяют устройства, величина погрешности у которых колеблется в диапазоне 0,05-0,5. Такие устройства принято называть прецезионными. Приборы с классом точности выше 1,0 являются техническими средствами и используются в тех сферах, где некоторая неточность не является критичной.

Подразделение приборов на классы в зависимости от величины погрешности регламентируется государственным стандартом, в котором четко прописано, для какого прибора какой категории допустима та или иная погрешность. Проверка средств измерений изначально производится на заводе-изготовителе. Так как в ходе эксплуатации погрешность, как и точность измерений, может терять первоначальные значения, все измерительные средства регулярно проходят процедуру поверки в специализированных центрах метрологии. В ходе этого процесса происходит сравнение показаний и величин измерений с эталонными значениями, после чего производят необходимую коррекцию.

fb.ru

5Бил. Класс точности си и его обозначение

Установление рядов пределов допускаемых погрешностей позволяет упорядочить требования к средствам измерений по точности. Это упорядочивание осуществляется путем установления классов точности СИ. Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей, а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Класс точности СИ конкретного типа устанавливают в стандартах технических требований или других нормативных документах. При выражении предела допускаемой основной погрешности в форме абсолютной погрешности класс точности в документации и на средствах измерения обозначается прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения. Выражение класса точности через относительные и приведенную погрешности рассмотрено в предыдущем разделе В настоящее время по отношению к современным средствам измерений понятие класс точности применяется довольно редко. В основном он чаще всего используется для описания характеристик электроизмерительных приборов, аналоговых стрелочных приборов всех типов, некоторых мер длины, весов, гирь общего назначения, манометров. Примеры обозначение классов точности для различных форм выражения погрешности приведены в таблице.

Обозначение классов точности

Пределы допускаемой основной погрешности

Обозначения

Форма выражения погрешности

в документации

на приборе

γ = ± 1,5

Класс точности 1,5

1,5

Приведенная погрешность

δ = ± 0,5

Класс точности 0,5

0,5

Относительная погрешность, постоянная

δ = ± [ 0,02 + 0,01( xk/x –1)]

Класс точности 0,02/0,01

0,02/0,01

Относительная погрешность, возрастает с уменьшением х

4бил

Понятие погрешности измерений Непосредственной задачей измерения является определение значений измеряемой величины. В результате измерения физической величины с истинным значением Хи мы получаем оценку этой величины Хизм. - результат измерений. При этом следует четко различать два понятия: истинные значения физических величин и их эмпирические проявления – действительные значения, которые являются результатами измерений и в конкретной измерительной задаче могут приниматься в качестве истинных значений. Истинное значение величины неизвестно и оно применяют только в теоретических исследованиях. Результаты измерений являются продуктами нашего познания и представляют собой приближенные оценки значений величин, которые находятся в процессе измерений. Степень приближения полученных оценок к истинным (действительным) значениям измеряемых величин зависит от многих факторов: метода измерений, использованных средств измерений и их погрешностей, от свойств органов чувств операторов, проводящих измерения, от условий, в которых проводятся измерения и т.д. Поэтому между истинным значением физической величины и результатом измерений всегда имеется различие, которое выражается погрешностью измерений (то же самое, что погрешностью результата измерений). Погрешность результата измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины:

∆X = Xизм - Xист

Так как истинное значение измеряемой величины всегда неизвестно и на практике мы имеем дело с действительными значениями величин Хд, то формула для определения погрешности в связи с этим приобретает вид:

∆X = Xизм - Xд

Погрешность СИ — разность между показанием средства измерений – Хп и истинным (действительным) значением измеряемой величины – Хд. Существует распространенная классификация погрешностей средств измерений. Ниже приводятся примеры их наиболее часто используемых видов. Абсолютная погрешность СИ – погрешность средства измерений, выраженная в единицах измеряемой величины: ∆Х = Хп – Хд. Абсолютная погрешность удобна для практического применения, т.к. дает значение погрешности в единицах измеряемой величины. Но при ее использовании трудно сравнивать по точности приборы с разными диапазонами измерений. Эта проблема снимается при использовании относительных погрешностей. Если абсолютная погрешность не изменяется во всем диапазоне измерения, то она называется аддитивной, если она изменяется пропорционально измеряемой величине (увеличивается с ее увеличением), то она называется мультипликативной Относительная погрешность СИ – погрешность средства измерений, выраженная отношением абсолютной погрешности СИ к результату измерений или к действительному значению измеренной величины: δ = ∆Х / Хд. Относительная погрешность дает наилучшее из всех видов погрешностей представление об уровне точности измерений, который может быть достигнут при использовании данного средства измерений. Однако она обычно существенно изменяется вдоль шкалы прибора, например, увеличивается с уменьшением значения измеряемой величины. В связи с этим часто используют приведенную погрешность. Приведенная погрешность СИ – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины ХN, которое называют нормирующим: γ = ∆Х / ХN. Относительные и приведенные погрешности обычно выражают либо в процентах, либо в относительных единицах (долях единицы). Для показывающих приборов нормирующее значение устанавливается в зависимости от особенностей и характера шкалы. Приведенные погрешности позволяют сравнивать по точности средства измерений, имеющие разные пределы измерений, если абсолютные погрешности каждого из них не зависят от значения измеряемой величины. По условиям проведения измерений погрешности средств измерений подразделяются на основные и дополнительные. Основная погрешность СИ – погрешность средства измерений, применяемого в нормальных условиях, т.е. в условиях, которые определены в НТД не него как нормальные. Нормальные значения влияющих величин указываются в стандартах или технических условиях на средства измерений данного вида в форме номиналов с нормированными отклонениями. Наиболее типичными нормальными условиями являются:

Иногда вместо номинальных значений влияющих величин указывается нормальная область их значений. Например, влажность (30–80)%. Дополнительная погрешность СИ – составляющая погрешности СИ, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения. Деление погрешностей на основные и дополнительные обусловлено тем, что свойства средств измерений зависят от внешних условий. Погрешности по своему происхождению разделяются на систематические и случайные. Систематическая погрешность СИ – составляющая погрешности средства измерений, принимаемая за постоянную или закономерно изменяющуюся. Систематические погрешности являются в общем случае функциями измеряемой величины и влияющих величин (температуры, влажности, давления, напряжения питания и т.п.). Случайная погрешность СИ – составляющая погрешности средства измерений, изменяющаяся случайным образом. Случайные погрешности средств измерений обусловлены случайными изменениями параметров составляющих эти СИ элементов и случайными погрешностями отсчета показаний приборов. При конструировании прибора его случайную погрешность стараются сделать незначительной в сравнении с другими погрешностями. У хорошо сконструированного и выполненного прибора случайная погрешность незначительна. Однако при увеличении чувствительности средств измерений обычно наблюдается увеличение случайной погрешности. Тогда при повторных измерениях одной и той же величины в одних и тех же условиях результаты будут различными. В таком случае приходится прибегать многократным измерениям и к статистической обработке получаемых результатов. Как правило, случайную погрешность приборов снижается до такого уровня, что проводить многократные измерений нет необходимости. Стабильность СИ — качественная характеристика средства измерений, отражающая неизменность во времени его метрологических характеристик. Градуировочная характеристика СИ – зависимость между значениями величин на входе и выходе средства измерений, полученная экспериментально. Может быть выражена в виде формулы, графика или таблицы.

9бил.

Классификация погрешностей измерений

Представленная классификация погрешностей измерений связана с причинами их возникновения. Кроме этого существуют и другие признаки, по которым классифицируются погрешности. По характеру проявления (свойствам погрешностей) они разделяются на систематические и случайные, по способам выражения - на абсолютные и относительные. Абсолютная погрешность выражается в единицах измеряемой величины, а относительная погрешность представляет собой отношение абсолютной погрешности к измеренному (действительному) значению величины и ее численное значение выражается либо в процентах, либо в долях единицы. Опыт проведения измерений показывает, что при многократных измерениях одной и той же неизменной физической величины при постоянных условиях погрешность измерений можно представить в виде двух слагаемых, которые по-разному проявляются от измерения к измерению. Существуют факторы, постоянно или закономерно изменяющиеся в процессе проведения измерений и влияющие на результат измерений и его погрешность. Погрешности, вызываемые такими факторами, называются систематическими. Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессирующие, периодические, изменяющиеся по сложному закону. Близость к нулю систематической погрешности отражает правильность измерений. Систематические погрешности обычно оцениваются либо путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений, либо использованием более точных средств измерений. Как правило, систематические погрешности стараются исключить с помощью поправок. Поправка представляет собой значение величины, вводимое в неисправленный результат измерения с целью исключения систематической погрешности. Знак поправки противоположен знаку величины. На возникновение погрешностей влияют также и факторы, нерегулярно появляющиеся и неожиданно исчезающие. Причем интенсивность их тоже не остается постоянной. Результаты измерения в таких условиях имеют различия, которые индивидуально непредсказуемы, а присущие им закономерности проявляются лишь при значительном числе измерений. Погрешности, появляющиеся в результате действия таких факторов, называются случайными погрешностями. Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью. Незначительность случайных погрешностей говорит о хорошей сходимости измерений, то есть о близости друг к другу результатов измерений, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях и с одинаковой тщательностью. Обнаруживаются случайные погрешности путем повторных измерений одной и той же величины в одних и тех же условиях. Они не могут быть исключены опытным путем, но могут быть оценены при обработке результатов наблюдений. Деление погрешностей измерений на случайные и систематические очень важно, т.к. учет и оценка этих составляющих погрешности требует разных подходов. Факторы, вызывающие погрешности, как правило, можно свести к общему уровню, когда влияние их на формирование погрешности является более или менее одинаковым. Однако некоторые факторы могут проявляться неожиданно сильно, например, резкое падение напряжения в сети. В таком случае могут возникать погрешности, существенно превышающие погрешности, оправданные условиями измерений, свойствами средств измерений и метода измерений, квалификацией оператора. Такие погрешности называются грубыми, или промахами. Грубая погрешность (промах) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных значений погрешности. Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных промахов при проведении измерений. Если же причины появления резко выделяющихся наблюдений установить нельзя, то для решения вопроса об их исключении используют статистические методы. Существует несколько критериев, которые позволяют выявить грубые погрешности. Некоторые из них рассмотрены ниже в разделе об обработке результатов измерений.

8

Виды измерений По характеру зависимости измеряемой величины от времени измерения разделяются на: статические, при которых измеряемая величина остается постоянной во времени; динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени. Статическими измерениями являются, например, измерения размеров тела, постоянного давления, электрических величин в цепях с установившемся режимом, динамическими - измерения пульсирующих давлений, вибраций, электрических величин в условиях протекания переходного процесса. По способу получения результатов измерений их разделяют на: прямые; косвенные; совокупные; совместные. Прямые - это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой , где- искомое значение измеряемой величины, а- значение, непосредственно получаемое из опытных данных. При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др.Косвенные - это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле , где- функциональная зависимость, которая заранее известна,- значения величин, измеренных прямым способом. Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения. Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка.Совокупные - это производимые одновременно измерения нескольких одноименных величин, при которых искомую величину определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь). Совместные - это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними. В качестве примера можно назвать измерение электрического сопротивления при 200С и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах.

Методы измерений Метод измерения – это способ экспериментального определения значения физической величины, т. е. совокупность используемых при измерениях физических явлений и средств измерений. Метод непосредственной оценки заключается в определения значения физической величины по отсчетному устройству измерительного прибора прямого действия. Например – измерение напряжения вольтметром. Этот метод является наиболее распространенным, но его точность зависит от точности измерительного прибора. Метод сравнения с мерой – в этом случае измеряемая величина сравнивается с величиной, воспроизводимой мерой. Точность измерения может быть выше, чем точность непосредственной оценки. Различают следующие разновидности метода сравнения с мерой: Метод противопоставления, при котором измеряемая и воспроизводимая величина одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между величинами. Пример: измерение веса с помощью рычажных весов и набора гирь. Дифференциальный метод, при котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой. При этом уравновешивание измеряемой величины известной производится не полностью. Пример: измерение напряжения постоянного тока с помощью дискретного делителя напряжения, источника образцового напряжения и вольтметра. Нулевой метод, при котором результирующий эффект воздействия обеих величин на прибор сравнения доводят до нуля, что фиксируется высокочувствительным прибором – нуль-индикатором. Пример: измерение сопротивления резистора с помощью четырехплечевого моста, в котором падение напряжения на резисторе с неизвестным сопротивлением уравновешивается падением напряжения на резисторе известного сопротивления. Метод замещения, при котором производится поочередное подключение на вход прибора измеряемой величины и известной величины, и по двум показаниям прибора оценивается значение измеряемой величины, а  затем подбором известной величины добиваются, чтобы оба показания совпали. При этом методе может быть достигнута высокая точность измерений при высокой точности меры известной величины и высокой чувствительности прибора. Пример: точное точное измерение малого напряжения при помощи высокочувствительного гальванометра, к которому сначала подключают источник неизвестного напряжения и определяют отклонение указателя, а затем с помощью регулируемого источника известного напряжения добиваются того же отклонения указателя. При этом известное напряжение равно неизвестному. Метод совпадения, при котором измеряют разность между измеряемой величиной и величиной, воспроизводимой мерой, используя совпадение отметок шкал или периодических сигналов. Пример: измерение частоты вращения детали с помощью мигающей лампы стробоскопа: наблюдая положение метки на вращающейся детали в моменты вспышек лампы, по известной частоте вспышек и смещению метки определяют частоту вращения детали.

2 И 3

    1. Статическая погрешность измерений

Погрешность результата измерений, свойственная условиям статического измерения

    1. Динамическая погрешность измерений

Погрешность результата измерений, свойственная условиям динамического измерения.

20 Б Элекродинамические измерительные приборы

Устройство электродинамического механизма и векторная диаграмма, поясняющая его работу, приведены на рисунке:

Электродинамический измерительный механизм работает по принципу взаимодействия магнитных потоков двух катушек. Электродинамический механизм состоит из двух катушек. Одна из них подвижная, а другая укреплена неподвижно. Токи, протекающие по этим катушкам и магнитные потоки ими образуемые при своем взаимодействии создают вращающий момент.

Приборы электродинамической системы имеют малую чувствительность и большое самопотребление. Применяются в основном при токах 0.1…10А и напряжениях до 300 В.

19 Б

Электромагнитные измерительные приборы

Устройство измерительного механизма электромагнитного типа показано на рисунке:

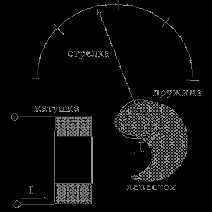
В электромагнитных измерительных механизмах для создания вращающего момента используется действие магнитного поля катушки с током на подвижный ферромагнитный (чаще пермоллоевый) лепесток. Достоинства электромагнитных механизмов: пригодность для работы в цепях постоянного и переменного тока; большая перегрузочная способность; возможность непосредственного измерения больших токов и напряжений; простота конструкции. Недостатки электромагнитных механизмов: неравномерная шкала; невысокая чувствительность; большое самопотребление мощности; подверженность влиянию изменения частоты; подверженность влиянию внешних магнитных полей и температуры.

21БИЛ

Электростатические измерительные приборы

Схемы механизмов различных конструкций показаны на рисунке. На рисунке а приведена схема с изменяющейся площадью электродов, а на рисунке б- с изменяющимся расстоянием между электродами.

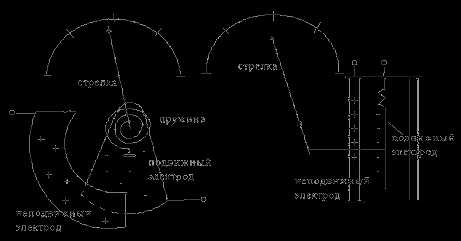
Принцип действия электростатического измерительного механизма основан на взаимодействии сил, возникающих между двумя разнозаряженными пластинами. Достоинства электростатических приборов: высокое входное сопротивление, малую входную емкость, малую мощность самопотребления, широкий частотный диапазон, могут использоваться в цепях переменного и постоянного тока, показания не зависят от формы кривой измеряемого сигнала. Недостатки электростатических приборов: приборы имеют малую чувствительность и невысокую точность.

31БИЛ

. Цифровые измерительные устройства.

Это устройства, автоматически вырабатывающие дискретные сигналы цифровой информации и показания представляются в цифровом виде.

Вырабатывает цифровой код в соответствии с измеряемой величиной, при этом непрерывная аналоговая величина квантуется по уровню и дискретизируется во времени.

Дискретизация во времени – преобразование, при котором значение величины отличается от 0 и совпадает с соответствующим значением измеряемой величины только в определенные моменты времени. Промежутки между этими значениями – шаг дискретизации.

Квантование по уровню – преобразование, при котором непрерывная аналоговая величина принимает фиксированные, квантованные значения. Эти значения – уровни квантования или кванты.

Важной характеристикой является правило отождествления измеряемой величины и уровней квантования. ----------------

studfiles.net