Математика курс лекций 1 курс / Лекция 4. Матрицы и определители. Формула определителя матрицы
Определитель матрицы.
Навигация по странице:
Определитель матрицы или детерминант матрицы - это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.Определение.
Определителем матрицы n×n будет число:| det(A) = | Σ | (-1)N(α1,α2,...,αn)·aα11·aα22·...·aαnn |
| (α1,α2,...,αn) |
Обозначение
Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).Свойства определителя матрицы
Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
- При транспонировании значение определителя матрицы не меняется:
det(A) = det(AT)
- Определитель обратной матрицы:
det(A-1) = det(A)-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
- Общий множитель в строке (столбце) можно выносить за знак определителя:
a11a12...a1na21a22...a2n....k·ai1k·ai2...k·ain....an1an2...ann = k·a11a12...a1na21a22...a2n....ai1ai2...ain....an1an2...ann
- Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени: B = k·A => det(B) = kn·det(A) где A матрица n×n, k - число.
- Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
a11a12...a1na21a22...a2n....bi1 + ci1bi2 + ci2...bin + cin....an1an2...ann = a11a12...a1na21a22...a2n....bi1bi2...bin....an1an2...ann + a11a12...a1na21a22...a2n....ci1ci2...cin....an1an2...ann
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
- Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)
Методы вычисления определителя матрицы
Вычисление определителя матрицы 1×1
Правило:
Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:∆ = |a11| = a11
Вычисление определителя матрицы 2×2
Правило:
Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:| ∆ = | = a11·a22 - a12·a21 |
Пример 1.
Найти определитель матрицы A| A = |
|
Решение:
| det(A) = | = 5·1 - 7·(-4) = 5 + 28 = 33 |
Вычисление определителя матрицы 3×3
Правило треугольника для вычисления определителя матрицы 3-тего порядка
Правило:
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.| + | – |
| ∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 - a13·a22·a31 - a11·a23·a32 - a12·a21·a33
Правило Саррюса для вычисления определителя матрицы 3-тего порядка
Правило:
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":| ∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 - a13·a22·a31 - a11·a23·a32 - a12·a21·a33
Пример 2.
Найти определитель матрицы A = 571-410203Решение:
det(A) = 571-410203 = 5·1·3 + 7·0·2 + 1·(-4)·0 - 1·1·2 - 5·0·0 - 7·(-4)·3 = 15 + 0 + 0 - 2 - 0 + 84 = 97Вычисление определителя матрицы произвольного размера
Разложение определителя по строке или столбцу
Правило:
Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:| n | |||
| det(A) = | Σ | aij·Aij | - разложение по i-той строке |
| j = 1 |
Правило:
Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:| n | |||
| det(A) = | Σ | aij·Aij | - разложение по j-тому столбцу |
| i = 1 |
При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.
Пример 3.
Найти определитель матрицы A| A = |
|
Решение: Вычислим определитель матрицы разложив его по первому столбцу:
= 2·(-1)1+1· 2111 + 0·(-1)2+1· 4111 + 2·(-1)3+1· 4121 == 2·(2·1 - 1·1) + 2·(4·1 - 2·1) = 2·(2 - 1) + 2·(4 - 2) = 2·1 + 2·2 = 2 + 4 = 6
Пример 4.
Найти определитель матрицы AA = 2411020021134023
Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):
det(A) = 2411020021134023 = - 0· 411113023 + 2· 211213423 - 0· 241213403 + 0· 241211402 == 2·(2·1·3 + 1·3·4 + 1·2·2 - 1·1·4 - 2·3·2 - 1·2·3) = 2·(6 +12 + 4 - 4 - 12 - 6) = 2·0 = 0
Приведение определителя к треугольному виду
Правило:
Используя свойства определителя для элементарных преобразований над строками и столбцами 8 - 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.Пример 5.
Найти определитель матрицы A приведением его к треугольному видуA = 2411021021134023
Решение:
det(A) = 2411021021134023
Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:
det(A) = 241102102 - 21 - 41 - 13 - 14 - 2·20 - 4·22 - 1·23 - 1·2 = 241102100-3020-801
Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):
det(A) = - 2141012000-3200-81
Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:
det(A) = - 214 + 1·81012 + 0·8000-3 + 2·8200-8 + 1·81 = - 211210120001320001 = -2·1·13·1 = -26
Теорема Лапласа
Присоединяйтесь
© 2011-2018 Довжик МихаилКопирование материалов запрещено.Добро пожаловать на OnlineMSchool.Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]
ru.onlinemschool.com
Определитель матрицы 2x2, 3x3, 4x4...
Определитель (детерминант) квадратной матрицы A - это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.
Обозначения
Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$
Свойства определителя
- Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12$\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$
- Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13$\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$
- Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14$\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)или$\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны)
- Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15$\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или
$ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
- При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 16В определителе$\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:$3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:$6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$
- При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.
Пример 17$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$ Пример 18$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$
- При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.
Пример 19$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$
Пример 20$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$
- Определитель матрицы равен определителю транспонированной матрицы.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
Один из миноров матрицы A есть $\begin{vmatrix} 1 & 2\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
www.math10.com
Определитель, детерминант матрицы
Способы вычисления определителя матрицы
Определителем матрицы второго порядка называется число, равное
Определитель матрицы третьего порядка
Определитель матрицы третьего порядка можно вычислить, используя правило треугольника или правило Саррюса.
Правило треугольника. Определителем матрицы третьего порядка можно вычислить по формуле
Схематически это правило можно изобразить следующим образом
Правило Саррюса. Для вычисления определителя третьего порядка, допишем два первых столбца и перемножим диагональные элементы, взяв произведение со знаком «плюс», если диагональ является главной или параллельна её и, взяв произведение со знаком «минус», если диагональ является побочной или параллельной ей, получим
Вычисление определителей высших порядков
Для вычисления определителей высших порядков, используется способ разложения определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения. При этом вычисление определителя -го порядка сводится к вычислению определителей -го порядка.
Свойства определителя матрицы
Определитель любого порядка может быть вычислен с использованием свойств определителя:
- определитель не изменяется при элементарных преобразованиях строк или столбцов;
- при перестановке строк или столбцов знак определителя меняется на противоположный;
- определитель треугольной матрицы равен произведению элементов расположенных на диагонали. Например, для верхнетреугольной матрицы
определитель равен
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Лекция 4. Матрицы и определители
Матрицы и определители. Лекция 4.
Матрицы.
Основные понятия.
Матрицей называется прямоугольная таблица чисел.
Пример 13. , ,,.
В общем случае матрица может содержать строк истолбцов
.
Числа называютсяэлементами матрицы, где - указывает номер строки,- указывает номер столбца.
Элементы образуютглавную диагональ матрицы. Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров называетсяматрицей – го порядка.
Матрицы называются равными, если у них равны элементы, стоящие на соответствующих местах, т. е. тогда и только тогда, когда, для всех,.
Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной.
Пример 14. .
Если все элементы матрицы равны нулю, то матрица называется нулевой.
Пример 15. .
Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной.
Пример 16. , .
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю.
Пример 17. ,.
Матрица, содержащая одну строку (столбец), называется вектором (вектор-строкой, вектор-столбцом).
Пример 18. ,.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной .
Пример 19. ;
Очевидно, что .
Действия над матрицами.
Матрицы одинаковых размерностей можно складывать и вычитать. Если
, , то, причем
, для всех .
Пример 20. ,
.
Умножение матрицы на число.
Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.
Пример 21. Пусть , тогда. Матрицаназываетсяпротивоположной к матрице.
Умножение матриц.
Умножение матриц можно только в том случае, когда число столбцов матрицыравно числу строк матрицыВ этом случае справедливо соотношение, причем элементы матрицыравны,,. Другими словами строки матрицыумножаются на столбцы матрицы
Пример 22. Пусть ,. Тогда
,
.
Видим, что в общем случае . Если же выполняется условие, то матрицыиназываютсяперестановочными друг с другом.
Матрица называется ступенчатой, если для её элементов выполняются условия:
под первым не нулевым элементом каждой строки находится 0;
первый ненулевой элемент любой строки находится правее первого не нулевого элемента любой строки, расположенной выше.
Пример 23. Следующая матрица является ступенчатой.
.
Элементарные преобразования матриц.
Элементарными преобразованиями матриц являются:
Перестановка местами двух любых её строк (столбцов).
Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число.
Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Две матрицы называютсяэквивалентными, если одна из них получается из другой с помощью элементарных преобразований
Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
Определители.
Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.
Пример 24. Если , то. Так.
Если , то.
Так .
Если , то
. Так
.
При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.
С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.
Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.
Вычисление определителей более высоких порядков осуществляется путем использования их свойств.
Свойства определителей.
Пусть дана квадратная матрица
Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы и обозначается
Минором некоторого элемента определителя называют определитель, который получается вычеркиванием из негостроки истолбца. Например
, .
Алгебраическим дополнением элемента определителя называют число. Например
, .
Свойства определителей.
1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. е. .
2. Определитель меняет знак при перестановке любых двух его строк (столбцов).
3. Определитель, имеющий две равные строки (столбца), равен 0.
4. Общий множитель строки (столбца) можно выносить за знак определителя, например
.
5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например
6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.
(I=I+II).
7. Определитель треугольной матрицы равен произведению её диагональных элементов.
8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например
.
Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов.
9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.
22
studfiles.net
Как найти определитель матрицы
Определитель(он же determinant(детерминант)) находится только у квадратных матриц. Определитель есть ничто иное, как значение сочетающее в себе все элементы матрицы, сохранающееся при транспонировании строк или столбцов. Обозначаться он может как det(A), |А|, Δ(A), Δ, где А может быть как матрицей, так и буквой обозначающей ее. Найти его можно разными методами:
Все выше предложенные методы будут разобраны на матрицах размера от трех и выше. Определитель двумерной матрицы находится с помощью трех элементарных математических операций, поэтому ни в один из методов нахождение определителя двумерной матрицы не попадет. Ну кроме как дополнение, но об этом потом.
Найдем определитель матрицы размером 2х2:
Для того, чтобы найти определитель нашей матрицы, требуется вычесть произведение чисел одной диагонали из другой, а именно , то есть
Примеры нахождения определителя матриц второго порядка
Разложение по строке/столбцу
Выбирается любая строка или столбец в матрице. Каждое число в выбранной линии умножается на (-1)i+j где(i,j - номер строки,столбца того числа) и перемножается с определителем второго порядка, составленного из оставшихся элементов после вычеркивания i - строки и j - столбца. Разберем на матрице
- Выберем строку/столбец
Например возьмем вторую строку.
Примечание: Если явно не указано, с помощью какой линии найти определитель, выбирайте ту линию у которой есть ноль. Меньше будет вычислений.
- Составим выражение
Не трудно определить, что знак у числа меняется через раз. Поэтому вместо единиц можно руководствоваться такой таблицей:
- Поменяем знак у наших чисел
- Найдем определители у наших матриц
- Считаем все это
Решение можно написать так:
Примеры нахождения определителя разложением по строке/столбцу:
Метод приведения к треугольному виду(с помощью элементарных преобразований)
Определитель находится с помощью приведения матрицы к треугольному(ступенчатому) виду и перемножению элементов на главной диагонали
Треугольной матрицей называется матрица, элементы которой по одну сторону диагонали равны нулю.
При построении матрицы следует помнить три простых правила:
- Каждый раз при перестановке строк между собой определитель меняет знак на противоположный.
- При умножении/делении одной строки на не нулевое число, её следует разделить(если умножали)/умножить(если разделяли) на него же или же произвести это действие с полученным определителем.
- При прибавлении одной строки умноженной на число к другой строке, определитель не изменяется(умножаемая строка принимает своё исходное значение).
Попытаемся получить нули в первом столбце, потом во втором. Взглянем на нашу матрицу:
Та-а-ак. Чтобы вычисления были поприятнее, хотелось бы иметь самое близкое число сверху. Можно и оставить, но не надо. Окей, у нас во второй строке двойка, а на первой четыре.
Поменяем же эти две строки местами.
Поменяли строки местами, теперь мы должны либо поменять у одной строки знак, либо в конце поменять знак у определителя. Сделаем это потом.
Теперь, чтобы получить ноль в первой строке - умножим первую строку на 2.
Отнимем 1-ю строку из второй.
Согласно нашему 3-му правилу возващаем исходную строку в начальное положение.
Теперь сделаем ноль в 3-ей строке. Можем домножить 1-ую строку на 1.5 и отнять от третьей, но работа с дробями приносит мало удовольствия. Поэтому найдем число, к которому можно привести обе строки - это 6.
Умножим 3-ю строку на 2.
Теперь умножим 1-ю строку на 3 и отнимем из 3-ей.
Возвратим нашу 1-ю строку.
.
Не забываем, что умножали 3-ю строку на 2, так что потом разделим определитель на 2.
Один столбец есть. Теперь для того чтобы получить нули во втором - забудем про 1-ю строку - работаем со 2-й строкой. Домножим вторую строку на -3и прибавим к третьей.
Не забываем вернуть вторую строку.
Вот мы и построили треугольнаую матрицу. Что нам осталось ? А осталось перемножить числа на главной диагонали, чем и займемся.
Ну и осталось вспомнить, что мы должны разделить наш определитель на 2 и поменять знак.
Правило Саррюса(Правило треугольников)
Правило Саррюса применимо только к квадратным матрицам третьего порядка.
Определитель вычисляется путем добавления первых двух столбцов справа от матрицы, перемножением элементов диагоналей матрицы и их сложением, и вычитанием суммы противоположных диагоналей. Из оранжевых диагоналей вычитаем фиолетовые.
У правила треугольников то же, только картинка другая.
Пример
Теорема Лапласа см. Разложение по строке/столбцу
Наверх
kak-reshit.su
§9. Формула полного разложения определителя по элементам матрицы.
Теорема 1.2. detA = (;\s\do10(I(j1(1)I(j1,j2,…,jn)aj1; 1aj2; 2… ajn;n.
Поясним, что здесь записано. Мы выбираем в матрице n элементов, так чтобы из каждой строки и каждого столбца был выбран ровно один элемент. Мы расположим эти элементы в порядке возрастания номеров строк и составим их произведение. Тогда номера столбцов образуют перестановку I(j1,j2,…,jn). Если эта перестановка нечётная, то мы добавляем к произведению знак минус. Затем мы все такие произведения складываем. Число слагаемых равно числу различных перестановок (j1,j2,…,jn) нижних индексов, т.е. равно n!.
Например, множество индексов {1,2,3} имеет 6 перестановок:
(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1),
среди которых нечётными являются вторая, третья и шестая. Поэтому разложение определителя третьего порядка имеет вид
= a1;1a1;2a1;3+ a2;1a3;2a1;3+ a3;1a1;2a2;3a1;1a3;2a2;3a2;1a1;2a3;3a3;1a2;2a1;3.
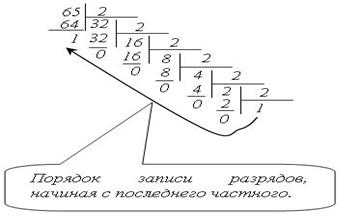
Эту формулу можно запомнить виде схемы
§10. Системы линейных уравнений. Правило Крамера.
Определение. Система из m линейных уравнений с n неизвестными (СЛУ) имеет вид:
(1.11)
Числа aij называются коэффициентами системы, а числа b1, b2,…, bm– свободными членами. Коэффициенты системы образуют матрицу A, а свободные члены – столбец B:
A= , B=
Символы x1, x2,…, xn называются неизвестными. Матрица
A*=
Называется расширенной матрицей СЛУ (8).
Определение. Решением системы линейных уравнений (1.11) (частным решением) называется любой набор чисел (1, 2,…, n), при подстановке которых вместо неизвестных x1, x2,…, xn все уравнения системы превращаются в верные равенства. Система называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.
Например, следующая система несовместна:
СЛУ может иметь более, чем одно решение. Тогда она имеет бесконечное количество решений. Например, все решения системы
можно записать в виде (12,),R (т.е. выступает здесь в качестве параметра: вместо мы можем подставить любое число, и получится частное решение). Такая запись называется общим решением системы.
Пусть теперь число уравнений в СЛУ равно числу неизвестных: m=n. Тогда матрица A является квадратной. Обозначим =detA, а i – определитель матрицы, которая получается из A заменой i-го столбца на столбец свободных членов B. Например,
1= .
Теорема 1.3. (Правило Крамера). Если 0, то СЛУ (1.11) (при m=n) имеет, и притом единственное решение. Это решение можно найти по формулам
x1= , x2= , …, xn= .
Обратите внимание, что данная теорема состоит из двух утверждений. Первое предложение о существовании и единственности решения имеет самостоятельное большое значение.
Пример 3. Найти решение системы уравнений
Решение.
== –2, 1= = 6, 2= = – 4.
x1 = = = –3, x2 = = = 2.
Ответ: (–3, 2).
§11. Ранг матрицы.
Определение. Рангом системы строк (системы столбцов) матрицы A называется максимальное количество её линейно независимых строк (столбцов). Т.е. говорим, что ранг системы строк матрицы A равен r1, если в матрице существует r1 линейно независимых строк, а любые r1+1 строк линейно зависимы; говорим, что ранг системы столбцов матрицы A равен r2, если в матрице существует r2 линейно независимых столбцов, а любые r2+1 столбцов линейно зависимы.
Определение. Рангом матрицы A называется максимальная размерность её ненулевого минора. Т.е. говорим, что ранг матрицы A равен r, если в ней существует ненулевой минор порядка r, а любой минор порядка r+1 равен нулю (или таких миноров вообще нет).
Ранг матрицы обозначаем rankA или rkA. Если L – ненулевой минор порядка r, то он называется базисным минором. В матрице может быть несколько базисных миноров. Строки и столбцы, в которых расположен базисный минор будем называть базисными.
Пример 3. В следующей матрице первая и вторая строки пропорциональны, а третья строка им не пропорциональна.
A= .
Поэтому в матрице есть 2 линейно независимые сроки, а 3 строки линейно зависимы. Значит ранг системы строк матрицы A равен 2.
Минор
L12;23 = 0,
а любой минор порядка три должен включать в себя часть первой и часть второй сроки. Поэтому любой минор порядка 3 равен нулю. Значит, L12;23 – базисный минор и rankA=2. Также базисными будут миноры L13;23 , L14;23 , L34;23 , L24;23 .
Перебирать все миноры в поисках базисного – это очень трудоёмкая задача. Поэтому можно использовать метод окаймляющих миноров. Если мы нашли ненулевой минор L порядка k, то мы затем перебираем не все миноры порядка k+1, а только те, которые содержат в себе минор L (их будем называть окаймляющими). Если все окаймляющие миноры окажутся равными нулю, то и все миноры порядка k+1 тоже будут равны нулю, и мы сделаем вывод, что rankA=k. Если среди окаймляющих миноров мы найдём ненулевой минор L, то переходим к минорам порядка k+2, которые содержат в себе L, и т.д.
Другой метод вычисления ранга матрицы и нахождения базисного минора – это метод Гаусса. С подобным методом мы уже познакомились, когда приводили матрицу к треугольному виду с целью вычислить её определитель. При вычислении ранга матрицы мы можем позволить себе больше видов действий.
Назовём элементарными преобразованиями матрицы следующие преобразования.
1. Вычёркивание срок и столбцов, которые состоят только из нулей.
2. Перестановка строк или столбцов.
3. Умножение строки или столбца на число не равное нулю.
4. Прибавление к одной строке (столбцу) матрицы другой строки (столбца), домноженной на некоторое число.
Предложение 4. Элементарные преобразования не изменяют ранга матрицы.
Шаг 1. Вычеркнем все строки и столбцы, состоящие только из нулей.
Шаг 2. В первом столбце матрицы выберем ненулевой элемент и строку, в которой он находится, поставим на первое место.
Шаг 3. Разделим первую строку на a1;1. К каждой i-ой строке матрицы прибавим первую строку, домноженную на число a1; i. В результате мы получим матрицу вида
A= .
Шаг 4. Совершаем те же действия над матрицей
B=,
совершая их на самом деле над всей матрицей. Т.е., если в матрице B какой-либо столбец равен нулю, то мы вычёркиваем его во всей матрице A. В результате мы получим матрицу вида
A= .
Шаг 5. Совершаем те же самые действия, которые были описаны выше с матрицей
,
совершая на самом деле их над всей матрицей A.
В конечном итоге мы получим матрицу вида
, (1.12)
определитель которой равен 1. Сколько в этой матрице осталось строк и столбцов, таков и ранг матрицы. Для того, чтобы указать в исходной матрице A базисный минор, надо вспомнить какие номера в ней имели оставшиеся не вычеркнутыми строки и столбцы. В этих сроках и столбцах находится базисный минор.
В процессе преобразований мы вычеркнули все строки, которые не были базисными, т.е. они превратились в нулевые. До этого мы прибавляли к ним другие строки, домноженные на некоторые числа. Получается, что небазисные строки являются линейной комбинацией тех строк, которые мы к ним прибавляли. Мы могли совершать элементарные преобразования над столбцами матрицы и прийти к аналогичному выводу для столбцов. Отсюда вытекает теорема.
Теорема 1.4. (О базисном миноре) Любая строка матрицы является линейной комбинацией базисных строк, а любой столбец – линейной комбинацией базисных столбцов.
Следующую теорему примем без доказательства.
Теорема 1.5. (О ранге матрицы) Ранг системы строк матрицы равен рангу системы столбцов и равен рангу матрицы.
Мы можем продолжить элементарные преобразования матрицы (1.12) и с помощью единиц, стоящих на диагонали занулить все элементы, обозначенные звёздочками. В результате мы получим единичную матрицу. Тем самым мы базисный минор можем привести к виду единичной матрицы. Если исходная матрица A является квадратной и для неё detA0, то этот определитель и будет её базисным минором. При этом все столбцы будут базисными, и нам не придётся вычёркивать столбцы в процессе элементарных преобразований. Отсюда вытекает теорема.
Теорема 1.6. Если для квадратной матрицы detA0, то с помощью элементарных преобразований одних только строк матрицы мы можем привести эту матрицу к виду единичной матрицы.
Если не вычёркивать столбцы в матрице, но допускать их перестановку, то с помощью элементарных преобразований строк мы можем привести матрицу к виду
.
Для этого нам понадобится на первое место переставить базисные столбцы. Все оставшиеся не вычеркнутыми строки будут базисными и их количество равно рангу матрицы. Этот результат окажется нам очень полезным, когда мы будем вести речь о решении СЛУ методом Гаусса. Затем, с помощью выделенных единиц мы можем занулить все стоящие выше их элементы и наша матрица примет вид
. (1.13)
Теорема 1.4. Если для квадратной матрицы detA=0, её строки столбцы линейно зависимы (без доказательства).
studfiles.net
Определитель матрицы | Virtual Laboratory Wiki
Определи́тель (или детермина́нт[1]) — одна из важнейших характеристик квадратных матриц. Определитель матрицы размера $ n\times n $ равен ориентированному $ n $-мерному объёму параллелепипеда, натянутого на её векторы-строки (или столбцы).
Для матрицы $ n\times n $ определитель выражается в виде многочлена степени $ n $ от элементов матрицы, который представляет собой сумму произведений элементов матрицы со всевозможными комбинациями различающихся номеров строк и столбцов, причём в каждом из произведений элемент из любой строки и любого столбца ровно один. Каждому произведению приписывается знак плюс или минус в зависимости от чётности перестановки номеров.
Если элементами матрицы являются числа, то определитель — это тоже число. В общем случае определитель может быть функциональным, векторным и т. п., то есть, представлять собой иные выражения, составленные из элементов.
Определитель матрицы $ n\times n $ задаётся формулой:
$ \det(A) = |A| = \begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = \sum_{i=1}^{n!} (-1)^{p(i)} \cdot a_{1k_{i1}}a_{2k_{i2}} \ldots a_{nk_{in}} $где
- $ |A| $ и $ \det(A) $ — так обозначается определитель,
- $ k_{ij} $ − i-я перестановка последовательности $ k_1 = 1,..,n $, то есть, $ k_{1j} = j $
- $ p(i) $ − количество перестановок пар номеров в последовательности $ k_{1j} $, необходимое для того, чтобы она превратилась в последовательность $ k_{1j} $.
или формула для вычисления определителя по заданной строке матрицы:
$ \det(A) = |A| = \sum_{k=1}^{n} (-1)^{k+i} a_{ik} M_{ik} $где
ЗамечанияПравить
Можно выделить следующие особенности построения выражения для определителя матрицы n $ \times $ n:
- выражение есть сумма членов, каждый из которых состоит из n сомножителей
- количество слагаемых в сумме равно количеству перестановок n номеров, то есть, n!
- номера строк и столбцов элементов, входящих в одно слагаемое, не повторяются
- слагаемые входят в сумму либо с плюсом, либо с минусом, в зависимости от чётности перестановки
- слагаемое из элементов главной диагонали матрицы, то есть, $ a_{11}a_{22} \ldots a_{nn} $ входит с плюсом
Определитель матрицы 2 $ \times $ 2 Править
Для вычисления определителя матрицы размером 2 $ \times $ 2, перемножаются её элементы, стоящие на главной диагонали и из них вычитается произведение остальных элементов:
$ |A| = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a_{12}a_{21} $
На рисунке элементы, входящие в сумму с плюсом, помечены красным, а с минусом — синим.
Определитель матрицы 3 $ \times $ 3 Править
Для вычисления определителя матрицы размером 3 $ \times $ 3, строится шесть произведений следующим образом:
$ |A| = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{12}a_{21}a_{33} - a_{11}a_{23}a_{32} $
На рисунке элементы, входящие в сумму с плюсом, помечены красным, а с минусом — синим, каждой законченной фигуре из трёх точек соответствует один член суммы из трёх сомножителей.
Свойства определителей Править
- Определитель матрицы $ n\times n $ равен ориентированному $ n $-мерному объёму параллелепипеда, натянутого на её векторы-строки (или столбцы).
- Отсюда видно, что если строки линейно зависимы (соответствующие векторы лежат в подпространстве меньшей размерности), то объём и определитель равны нулю.
- Если матрицу транспонировать (сделать строки столбцами), то определитель не изменится. $ \det(A^T) = \det(A) $
- $ \det(AB) = \det(A)\det(B) $.
- Доказательство: Легко увидеть, что строки $ c_1,...,c_n $ матрицы AB получаются из строк $ a_1,...,a_n $ матрицы A умножением на B: $ c_i=a_i*B $ (i=1,..,n) => что при фиксированной матрице B det( AB) есть кососимметрическая полилинейная функция строк матрицы A. Пусть $ a_1=\dot{a_1}+\ddot{a_1} $, где $ \dot{a_1},\ddot{a_1} $ — какие-то строки => $ \det (a_1*B,a_2*B,...,a_n*B) $=$ \det ((\dot{a_1}+\ddot{a_1})*B,a_2*B,...,a_n*B) $=$ \det (\dot{a_1}*B+\ddot{a_1}*B,a_2*B,...,a_n*B) $=$ \det (\dot{a_1}*B,a_2*B,...,a_n*B)+\det (\ddot{a_1}*B,a_2*B,...,a_n*B) $ Так как det( AB) есть кососимметрическая полилинейная функция, то справедливо: $ \det(AB)=\det(EB)*\det(A)=\det(A)*\det(B) $.
- Определитель треугольной матрицы (в частности, конечно, и диагональной) равен произведению её диагональных элементов.
- Определитель косотреугольной матрицы равен произведению её элементов побочной диагонали со знаком $ (-1)^{n(n-1)/2}=(-1)^{[n/2]} $ ($ [x] $ — целая часть числа $ x $).
Следующие свойства определителей, касающиеся строк, справедливы также и для столбцов.
- Если строку (т.е. все ее элементы) умножить на некоторое число, то определитель умножится на то же самое число.
- Если у матрицы переставить две строки, то её определитель изменит знак на противоположный.
- Если две строки матрицы совпадают, то её определитель равен нулю.
- Если хотя бы одна строка нулевая, то определитель равен нулю.
- При добавлении к любой строке линейной комбинации других строк определитель не изменится.
- Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
- Сумма произведений всех элементов любой строки на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Специальные виды определителей Править
- ↑ термин определитель предпочтилен.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Определитель матрицы. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
ru.vlab.wikia.com