СРЕДНИЕ АБСОЛЮТНОЕ И КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЯ. Формула среднего квадратичного отклонения
формула в excel, какая используется для расчета
Программа Excel высоко ценится как профессионалами, так и любителями, ведь работать с нею может пользователь любого уровня подготовки. Например, каждый желающий с минимальными навыками «общения» с Экселем может нарисовать простенький график, сделать приличную табличку и т.д.
Вместе с тем, эта программа даже позволяет выполнять различного рода расчеты, к примеру, расчет коэффициента вариации, но для этого уже необходим несколько иной уровень подготовки. Впрочем, если вы только начали тесное знакомство с данной прогой и интересуетесь всем, что поможет вам стать более продвинутым юзером, эта статья для вас. Сегодня я расскажу, что собой представляет среднеквадратичное отклонение формула в excel, зачем она вообще нужна и, собственно говоря, когда применяется. Поехали!
Что это такое
Начнем с теории. Средним квадратичным отклонением принято называть квадратный корень, полученный из среднего арифметического всех квадратов разностей между имеющимися величинами, а также их средним арифметическим. К слову, эту величину принято называть греческой буквой «сигма». Стандартное отклонение рассчитывается по формуле СТАНДОТКЛОН, соответственно, программа делает это за пользователя сама.
Суть же данного понятия заключается в том, чтобы выявить степень изменчивости инструмента, то есть, это, в своем роде, индикатор родом из описательной статистики. Он выявляет изменения волатильности инструмента в каком-либо временном промежутке. С помощью формул СТАНДОТКЛОН можно оценить стандартное отклонение при выборке, при этом логические и текстовые значения игнорируются.
Формула
Помогает рассчитать среднее квадратичное отклонение в excel формула, которая автоматически предусмотрена в программе Excel. Чтобы ее найти, необходимо найти в Экселе раздел формулы, а уже там выбрать ту, которая имеет название СТАНДОТКЛОН, так что создать формулу в Excele очень просто.
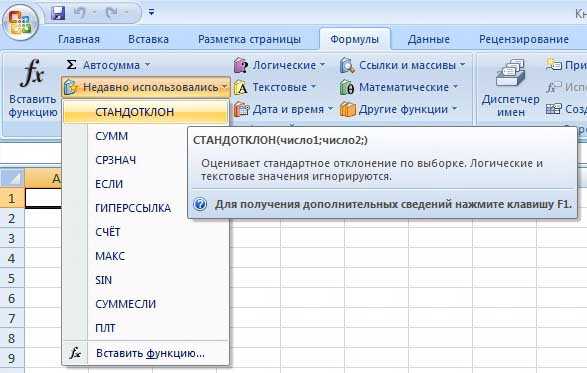
После этого перед вами появится окошко, в котором нужно будет ввести данные для вычисления. В частности, в специальные поля следует вписать два числа, после чего программа сама высчитает стандартное отклонение по выборке.

Бесспорно, математические формулы и расчеты – вопрос достаточно сложный, и не все пользователи с ходу могут с ним справиться. Тем не менее, если копнуть немного глубже и чуть более детально разобраться в вопросе, оказывается, что не все так уж и печально. Надеюсь, на примере вычисления среднеквадратичного отклонения вы в этом убедились.
Видео в помощь
userologia.ru
Оценка дисперсии, среднеквадратичное отклонение. — КиберПедия
Оценка дисперсии (S2) и среднеквадратичного отклонения (S) производится по формулам:
Выборочная дисперсия (S2) определяется по формуле:
Где:
- объем выборки;
| mi– частота встречаемости значения признака хi; |
Хi -случайные (текущие) величины;
X̅–среднее значение случайных величин по выборке, рассчитывается по формуле:
Итак, дисперсия - это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности.
Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, мы просто рассчитываем среднюю арифметическую.
Разгадка магического слова «дисперсия» заключается всего в этих трех словах: средний – квадрат – отклонений.
Среднее квадратичное отклонение (СКО)
Извлекая из дисперсии квадратный корень, получаем, так называемое «среднеквадратичное отклонение». Встречаются названия «стандартное отклонение» или «сигма» (от названия греческой буквыσ.). Формула среднего квадратичного отклонения имеет вид:
.
Итак, дисперсия – это сигма в квадрате, или – среднее квадратичное отклонение в квадрате.
Среднеквадратичное отклонение, очевидно, также характеризует меру рассеивания данных, но теперь (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые (это явствует из формулы расчета). Размах вариации – это разница между крайними значениями. Среднеквадратичное отклонение, как мера неопределенности, также участвует во многих статистических расчетах. С ее помощью устанавливают степень точности различных оценок и прогнозов. Если вариация очень большая, то стандартное отклонение тоже получится большим, следовательно, и прогноз будет неточным, что выразится, к примеру, в очень широких доверительных интервалах.
Поэтому в методах статистической обработки данных в оценках объектов недвижимости в зависимости от необходимой точности поставленной задачи используют правило двух или трех сигм.
Для сравнения правила двух сигм и правила трех сигм используем формулу Лапласа:
Ф— Ф,
где Ф(x) – функция Лапласа;
= минимальное значение
β = максимальное значение
s = значение сигмы (среднее квадратичное отклонение)
a = среднее значение
Правило двух сигм
Почти достоверно (с доверительной вероятностью 0,954) можно утверждать, что все значения случайной величины X с нормальным законом распределения отклоняются от ее математического ожидания M(X) = a на величину, не большую 2s (двух средних квадратических отклонений). Доверительной вероятностью (Pд) называют вероятность событий, которые условно принимаются за достоверные (их вероятность близка к 1).
Проиллюстрируем правило двух сигм геометрически. На рис. 6 изображена кривая Гаусса с центром распределения а. Площадь, ограниченная всей кривой и осью Оx, равна 1 (100%), а площадь криволинейной трапеции между абсциссами а–2s и а+2s, согласно правилу двух сигм, равна 0,954 (95,4% от всей площади). Площадь заштрихованных участков равна 1-0,954 = 0,046 (»5% от всей площади). Эти участки называют критической областью значений случайной величины. Значения случайной величины, попадающие в критическую область, маловероятны и на практике условно принимаются за невозможные.

Вероятность условно невозможных значений называют уровнем значимости случайной величины. Уровень значимости связан с доверительной вероятностью формулой:
= 1-,
где q – уровень значимости, выраженный в процентах.
Правило трех сигм
При решении вопросов, требующих большей надежности, когда доверительную вероятность (Pд) принимают равной 0,997 (точнее - 0,9973), вместо правила двух сигм, согласно формуле (3), используют правило трех сигм.
Согласно правилу трех сигм при доверительной вероятности 0,9973 критической областью будет область значений признака вне интервала (а-3s, а+3s). Уровень значимости составляет 0,27%.
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. Т.е. выборка высокоточная.
В этом и состоит сущность правила трех сигм:
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения (СКО).
На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
Уровень значимости принимают в зависимости от дозволенной степени риска и поставленной задачи. Для оценки недвижимости обычно принимается менее точная выборка, следуя правилу двух сигм.
cyberpedia.su
Квадратичное отклонение Википедия
Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок (измерений), это среднее арифметическое называют оценкой математического ожидания .
В литературе обычно обозначают греческой буквой σ{\displaystyle \sigma } (сигма) или буквой S{\displaystyle S}.
Основные сведения
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.
На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.
Стандартное отклонение на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[1]):
S=1n∑i=1n(xi−x¯)2.{\displaystyle S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}где S2{\displaystyle S^{2}} — выборочная дисперсия; xi{\displaystyle x_{i}} — i-й элемент выборки; n{\displaystyle n} — объём выборки; x¯{\displaystyle {\bar {x}}} — среднее арифметическое выборки (выборочное среднее):
x¯=1n∑i=1nxi=1n(x1+…+xn).{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}Само по себе, однако, S0{\displaystyle S_{0}} не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.
Обе оценки являются состоятельными[1].
В более общем случае среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[2]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии.
Правило трёх сигм
Правило трёх сигм (3σ{\displaystyle 3\sigma }) — практически все значения нормально распределённой случайной величины лежат в интервале (x¯−3σ;x¯+3σ){\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)}. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x¯{\displaystyle {\bar {x}}} истинная, а не полученная в результате обработки выборки).
Интерпретация величины среднеквадратического отклонения
Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение
На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.
Экономика и финансы
Среднее квадратическое отклонение доходности портфеля σ=D[X]{\displaystyle \sigma ={\sqrt {D[X]}}} отождествляется с риском портфеля.
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.
Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
См. также
Примечания
- ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
- ↑ C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — DOI:10.1088/1674-1137/40/10/100001.
Литература
- Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. — СПб.: Питер, 2003. — 688 с. — ISBN 5-272-00078-1..
wikiredia.ru
СРЕДНИЕ АБСОЛЮТНОЕ И КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЯ
⇐ ПредыдущаяСтр 5 из 8Следующая ⇒Степень разнообразия признака более точно выражается рядом других показателей.
При проверке вычисления средней арифметической скорости роста оврагов, были найдены центральные отклонения (хi- ) (табл. 1), которые представляли следующий ряд чисел: -2, -1,0, 1,2. Среднюю арифметическую из абсолютных значений этих чисел называютсредним абсолютным отклонением и обозначают буквой q (тета). Формула среднего абсолютного отклонения будет иметь следующий вид:
В математической статистике отдают предпочтение другому показателю степени колеблемости -среднему квадратическому отклонению, который вычисляется следующим образом. Каждое центральное отклонение возводится в квадрат. Затем находят среднюю арифметическую из этих квадратов и извлекают из нее квадратный корень. Формула среднего квадратического отклонения:
где d (сигма) - знак среднего квадратического отклонения. Схема вычисления дана в таблице 6.
Более правильно в знаменателе подкоренного выражения ставить не n, a n - 1. Однако при достаточно большом числе наблюдений уменьшение знаменателя на 1 практически не скажется на значении δ.
Таблица 6. Схема, облегчающая вычисление среднего квадратического отклонения
| x | хi- | (хi- )2 |
| -2 | ||
| -1 | ||
| о | ||
| 15 Итого |
Результаты вычислений могут быть записаны в следующем виде:
= 3 d = 1,6 м/год. Эта запись сжато передает основные свойства скоростей роста совокупности изучаемых оврагов: среднюю скорость их роста и границы средней колеблемости. Назовем = 3 простейшей математико-статистической моделью изучаемого показателя.
Средние квадратические отклонения обычно несколько больше средних абсолютных отклонений (примерно на 1/4).
Вычисление взвешенного среднего квадратического отклонения при сгруппированных данных производится по формуле
Таблица 7. Схема вычисления среднего арифметического и среднего квадратического отклонения
| Интервалы длин оврагов | Центры интервалов х | Число оврагов M | х • m | X; -X | (х,-х)2 | ( -)•) |
| 10-20 | -22 | |||||
| 20-30 | -12 | |||||
| 30-40 | -2 | |||||
| 40-50 | ||||||
| 50-60 | ||||||
| Итого: | 25 925 2600 |
Следовательно, длины 25 рассмотренных оврагов можно охарактеризовать двумя числами: 37 ± 10,2 м.
В теоретических формулах d часто выступает возведенной в квадрат. Эта величина называетсядисперсией. Она также является мерой колеблемости признака.
Средние квадратические отклонения климатических, почвенных, экономических показателей строго закономерны в пределах изучаемых территорий и отрезков времени. К сожалению, до сих пор при изучении колеблемости признаков географы весьма редко прибегают к вычислению d и даже q, а ограничиваются рассмотрением более простого, но менее корректного показателя колеблемости -размаха. Пример: основной показатель вертикального расчленения рельефа обычно представляет собой разность максимальной и минимальной высот. По матеатико-статистической терминологии это «размах» высот. Правильнее было бы вычислить d или хотя бы q.
КОЭФФИЦИЕНТ ВАРИАЦИИ
Среднее квадратическое отклонение является размерным показателем колеблемости признака. Оно выражается в тех же единицах, что и варианты признака. Поэтому сигма может служить непосредственным показателем колеблемости только тогда, когда сравниваются однородные количественные признаки. Пример сравнения колеблемости неоднородных признаков: имеются данные о значениях средних квадратических отклонений следующих показателей природных условий в одном и том же районе (табл. 8):
Таблица 8. Сравнение неоднородных признаков
| Признаки | 5 |
| 1. Длины оврагов | 100 м |
| 2. Распаханность площадей водосборов | 20% |
| 3. Углы наклона площадей водосборов | 0,5 |
По этим числам невозможно установить, какой из приведенных признаков варьирует больше, а какой меньше. Действительно, метры нельзя сравнить с процентами и градусами, так как единицы измерения оказываются разными. Поэтому для сравнения разнородных признаков введен особый показатель - коэффициент вариации (V), представляющий собой отношение d к . Обычно коэффициент вариации выражается в процентах, тогда его формула будет иметь следующий вид:
Зная средние арифметические и средние квадратические отклонения признаков, указанные в нашем примере, по формуле (6) можно вычислить коэффициенты вариации (см. табл. 9).
Таблица 9. Схема вычисления коэффициента вариации
| Признаки | d | V | |
| 1. Длины оврагов | 200м | 100м | 50% |
| 2. Распаханность площадей водосборов | 80% | 20% | 25% |
| 3. Углы наклона площадей | 0,5 | 10% |
Оказалось, что на исследуемой территории наиболее изменчивым количественным признаком является длина оврагов (V1 = 50%), а наименее изменчивы углы наклона (V3 = 10%).
Обратим внимание на то, что коэффициент вариации применим для сравнения колеблемостей только тех количественных показателей, которые не могут принимать отрицательных значений. Этому условию полностью отвечают признаки, рассмотренные в таблице 9. Действительно, длины оврагов, распаханность и углы наклонов площадей водосборов немыслимы со знаком минус. То же можно сказать и о вещественных разновидностях продукции промышленного и сельскохозяйственного производств, о вещественных природных ресурсах (биологических, водных, минеральных). Не удовлетворяют отмеченному условию высоты земной поверхности, температуры, предельно-допустимые нормы концентраций (ПДК). В зависимости от выбора точки отсчета этих показателей будут изменяться значения вычисленных средних арифметических и зависимых от них коэффициентов вариации. Например, коэффициент вариации абсолютных высот земной поверхности окажется гораздо меньше коэффициента вариации относительных высот, началом отсчета которых служат самые различные высотные уровни. Аналогично численные значения коэффициента вариации температур будут зависеть от выбора точки их отсчета (точки кипения, замерзания и др.).
Читайте также:
lektsia.com