План урока по теме " Избавление от иррациональности в знаменателе дроби". Как избавиться от иррациональности в дроби
Иррациональность в знаменателе дроби
Если дробь содержит корень в знаменателе, то мы говорим об иррациональности в знаменателе дроби. Часто бывает необходимо освободиться от иррациональности в знаменателе дроби. То есть заменить исходную дробь, содержащую иррациональность в знаменателе на тождественно равную ей дробь, которая иррациональность не содержит. Как это сделать?
Общее правило такое: нужно числитель и знаменатель дроби умножить на выражение, сопряженное знаменателю дроби.
Выражение А называется сопряженным иррациональному выражению В, если произведение АВ не содержит знака корня, то есть произведение АВ является рациональным числом.
Рассмотрим примеры сопряженных выражений.
1. Иррациональное выражение В содержит квадратный корень.
Возможны два случая:
a) . В этом случае :
Например, чтобы исключить иррациональность из знаменателя в дроби , нужно числитель и знаменатель дроби умножить на , получим
Внимание! Обязательно умножаем на выражение, сопряженное знаменателю и числитель, и знаменатель дроби - только в этом случае мы получим дробь, тождественно равную исходной.
б) ,
В этом случае сопряженным выражением будет дополняющее до разности квадратов:
Для выражения сопряженным будет :
Соответственно, для выражения сопряженным будет :
Например, исключим иррациональность из знаменателя дроби
Для этого умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, то есть на
Получим:
2. Иррациональное выражение В содержит корень n-й степени:
В этом случае сопряженное выражение :
Пример: исключим иррациональность из знаменателя дроби
Умножим числитель и знаменатель дроби на выражение . Получим:
3. Иррациональное выражение В является одним из множителей в разложении на множители разности или суммы кубов. В этом случае сопряженным ему выражением будет второй множитель:
Исключим иррациональность из знаменателя дроби:
Рассмотрим пример упрощения выражения, содержащего иррациональность в знаменателе дроби.
Найти значение выражения:
Внимание! Если нужно упростить выражение, содержащее иррациональность в знаменателе, то первым делом исключаем иррациональность из знаменателя, даже если кажется, что без этого можно обойтись.
Итак, исключим иррациональность из знаменателя первой и второй дроби:
Подставим полученные выражения в исходное:
Итак,
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Урок алгебры по теме "Освобождение от иррациональности в знаменателе дроби"
Разделы: Математика
Цели урока:
- Повторить преобразование выражений, содержащих квадратный корень, с использованием формул сокращенного умножения.
- Выработать алгоритм освобождения от иррациональности в знаменателе дроби.
- Сформировать у учащихся навыки применения этого алгоритма при преобразовании выражений, содержащих иррациональность в знаменателе дроби.
Ход урока
1. Организационный момент.
2. Устная работа.
Задание 1. Объясните, почему верно равенство:
3. Изучение нового материала.
Задача. Преобразовать алгебраическое выражение к такому виду, чтобы знаменатель дроби не содержал знаков квадратных корней:
Решение.
Используем основное свойство дроби, то есть подбираем такой множитель, чтобы при умножении на него в знаменателе дроби не оказалось квадратных корней.
Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе.
Алгоритм освобождения от иррациональности в знаменателе дроби:
- Разложить знаменатель дроби на множители.
- Если знаменатель имеет вид или содержит множитель , то числитель и знаменатель следует умножить на . Если знаменатель имеет вид или или содержит множитель такого вида, то числитель и знаменатель дроби следует умножить соответственно на или на .
- Преобразовать числитель и знаменатель дроби , если возможно, то сократить полученную дробь.
Выражения вида и называются сопряженными.
4. Закрепление нового материала.
Используя алгоритм освобождения от иррациональности в знаменателе дроби решить следующие задания.
Задание 1. Освободите выражение от иррациональности в знаменателе.
Умение освобождаться от иррациональности в знаменателе во многих случаях облегчает тождественные преобразования выражений.
Задание 3. Упростить выражение.
Решение.
Ответ:
Решить по учебнику задание 15.74 (а, б), 15.98 (а, б).
5. Итог урока.
Д /з. п. 15 (стр. 74–75), № 15.39–15.46, 15.74 (в, г), 15.98 (в, г).
xn--i1abbnckbmcl9fb.xn--p1ai
Иррациональность в знаменателе дроби | Ластики.ру
Суть метода состоит в умножении и делении дроби на такое выражение, которое позволит исключить иррациональность (квадратные и кубические корни) из знаменателя и сделает его проще. После этого дроби проще привести к общему знаменателю и окончательно упростить исходное выражение.
Дробь можно освободить от иррациональности (от иррационального выражения) в в знаменателе, например, так:
Чтобы освободить дробь от иррациональности в числителе или в знаменателе, можно применять формулы сокращенного умножения, которые применительно к корням имеют вид:
Выражения
и
называются взаимно сопряженными выражениями. Их произведение равно разности подкоренных выражений:
Пример. Освободить дроби от иррациональности в знаменателе:
Решение.
Ответ:
Г) Избавьтесь от иррациональности в знаменателе (ЕГЭ)
Решение основано на основном свойстве дроби, позволяющим умножать числитель и знаменатель дроби на одно и то же, не равное нулю число. Чтобы избавиться от знаков радикала в знаменателе дроби, обычно используют ФСУ (формулы сокращенного умножения). Ведь если разность двух радикалов умножить на их сумму, то получится разность квадратов корней, т.е. получится выражение без знаков радикалов.
Д) Освободиться от иррациональности в знаменателе дроби:
Решение:
Помните: в математике главное – тренировка. Чем больше примеров Вы решаете, тем лучше Вы это делаете.
Ластики.ру желают Вам отличной учебы!
lastici.ru
Урок 19. Избавление от иррациональности в числителе или знаменателе дроби
Используя предыдущие преобразования радикалов, можно освобождать подкоренное выражение от дроби. Освободить подкоренное выражение от дроби: Чтобы из знаменателя можно было извлечь кубический корень, умножим оба члена дроби на 32. ПРИМЕР:Освободить подкоренное выражение от дроби:
Чтобы из знаменателя можно было извлечь корень четвёртой степени, умножим оба члена дроби на 2 (так как 8 = 23). Если подкоренное выражение – алгебраическая дробь, подобные примеры решаются аналогично. ПРИМЕР: ПРИМЕР: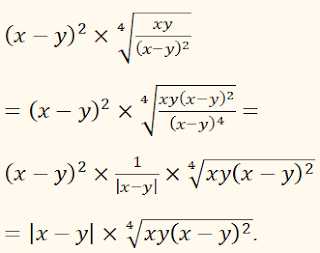
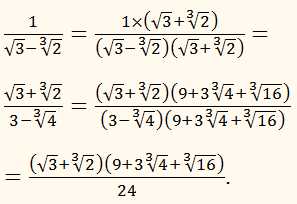 Если в знаменателе имеются три и более радикалов, то иногда полезно предварительно сгруппировать члены и свести данный случай к уже разобранным. ПРИМЕР: ПРИМЕР: Избавьтесь от знака корня в знаменателе дроби: Ближайшее натуральное число, превосходящее 3 и делящееся на 5, есть 5. Чтобы показатель шестёрки стал равен пяти, выражение в знаменателе надо умножить на Следовательно, освобождение от иррациональности в знаменатели дроби будет способствовать выражение На которое надо умножить числитель и знаменатель: ПРИМЕР: Избавьтесь от знака корня в знаменателе дроби: Очевидно, что ближайшее натуральное число, которое превосходит 15 и при этом делится без остатка на 4, это 16. Чтобы получить показатель степени в знаменателе равным 16, нужно умножить находящееся там выражение на Таким образом, умножение числителя и знаменателя исходной дроби на (заметим, значение этого выражение не равно нулю при любых действительных х) позволит избавиться от иррациональности в знаменателе: Задания к уроку 19
Если в знаменателе имеются три и более радикалов, то иногда полезно предварительно сгруппировать члены и свести данный случай к уже разобранным. ПРИМЕР: ПРИМЕР: Избавьтесь от знака корня в знаменателе дроби: Ближайшее натуральное число, превосходящее 3 и делящееся на 5, есть 5. Чтобы показатель шестёрки стал равен пяти, выражение в знаменателе надо умножить на Следовательно, освобождение от иррациональности в знаменатели дроби будет способствовать выражение На которое надо умножить числитель и знаменатель: ПРИМЕР: Избавьтесь от знака корня в знаменателе дроби: Очевидно, что ближайшее натуральное число, которое превосходит 15 и при этом делится без остатка на 4, это 16. Чтобы получить показатель степени в знаменателе равным 16, нужно умножить находящееся там выражение на Таким образом, умножение числителя и знаменателя исходной дроби на (заметим, значение этого выражение не равно нулю при любых действительных х) позволит избавиться от иррациональности в знаменателе: Задания к уроку 19 Как в дроби избавиться от иррациональности в знаменателе
Существует несколько типов иррациональности дроби в знаменателе. Она связана с присутствием в нем алгебраического корня одной или различных степеней. Чтобы избавиться от иррациональности, нужно выполнить определенные математические действия в зависимости от ситуации.Инструкция
- Прежде чем избавиться от иррациональности дроби в знаменателе, следует определить ее тип, и в зависимости от этого продолжать решение. И хотя любая иррациональность следует из простого присутствия корней, различные их комбинации и степени предполагают разные алгоритмы.
- Квадратный корень в знаменателе, выражение вида a/√bВведите дополнительный множитель, равный √b. Чтобы дробь не изменилась, умножать нужно и числитель, и знаменатель:a/√b → (a•√b)/b.Пример 1: 10/√3 → (10•√3)/3.
- Наличие под чертой дроби корня дробной степени вида m/n, причем n>mЭто выражение выглядит следующим образом:a/√(b^m/n).
- Избавьтесь от подобной иррациональности также путем ввода множителя, на этот раз более сложного: b^(n-m)/n, т.е. из показателя степени самого корня нужно вычесть степень выражения под его знаком. Тогда в знаменателе останется только первая степень:a/(b^m/n) → a•√(b^(n-m)/n)/b.Пример 2: 5/(4^3/5) → 5•√(4^2/5)/4 = 5•√(16^1/5)/4.
- Сумма квадратных корнейУмножьте обе составляющих дроби на аналогичную разность. Тогда из иррационального сложения корней знаменатель преобразуется в разность выражений/чисел под знаком корня:a/(√b + √c) → a•(√b - √c)/(b - c).Пример 3: 9/(√13 + √23) → 9•(√13 - √23)/(13 - 23) = 9•(√23 - √13)/10.
- Сумма/разность кубических корнейВыберите в качестве дополнительного множителя неполный квадрат разности, если в знаменателе стоит сумма, и соответственно неполный квадрат суммы для разности корней:a/(∛b ± ∛c) → a•(∛b² ∓ ∛(b•c) + ∛c²)/ ((∛b ± ∛c)• ∛b² ∓ ∛(b•c) + ∛c²) →a•(∛b² ∓ ∛(b•c) + ∛c²)/(b ± c).Пример 4: 7/(∛5 + ∛4) → 7•(∛25- ∛20 + ∛16)/9.
- Если в задаче присутствует и квадратный и кубический корень, тогда разделите решение на два этапа: последовательно выведите из знаменателя квадратный корень, а затем кубический. Делается это по уже известным вам методам: в первом действии нужно выбрать множитель разности/суммы корней, во втором – неполный квадрат суммы/разности.
completerepair.ru
План урока по теме " Избавление от иррациональности в знаменателе дроби"
Преобразование выражений, содержащих арифметические квадратные корни
Цель урока: создание условий для формирования умений, упрощать выражения, содержащие арифметические квадратные корни в ходе работы в группах сменного состава.
Задачи урока: проверить теоретическую подготовку учащихся, умение извлекать квадратный корень из числа, формировать навыки правильного воспроизведения своих знаний и умений, развивать вычислительные навыки, воспитывать умение работать в парах и ответственности за общее дело.
Ход урока.
I. Организационный момент. «ТАБЛИЦА ГОТОВНОСТИ»
Фиксация уровня готовности к началу занятия.
25 карточек красного цвета (5 баллов), желтого цвета (4 балла), синего
цвета (3 балла).
Таблица готовности
5 баллов (хочу знать, делать, решать)
4 балла (я готов к работе)
3 балла (я не очень хорошо себя чувствую, я не понимаю материал, мне нужна помощь)
II. Индивидуальная работа по карточкам
Карточка 1
Вынести множитель из-под знака корня:
Карточка 2
Внести множитель под знак корня:
3
Карточка 3
Упростить:а) б) в)
(Проверка после проверки домашнего задания)
III. Проверка домашнего задания.
№166, 167 устно фронтально
(самооценивание с помощью сигнальных карточек: зелёный - всё верно, красный – есть ошибка)
IV. Изучение нового материала. Работа в группах сменного состава.
Самостоятельно изучить материал, чтобы потом суметь объяснить его членам группы. Класс делится на 6 групп по 4 человека.
1, 2 и 3 группы – учащиеся со средними способностями
Как избавиться от иррациональности в знаменателе дроби? Рассмотрим общий случай и конкретные примеры.
Если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей, чтобы избавиться от иррациональности в знаменателе и числитель, и знаменатель дроби умножаем на квадратный корень из этого числа или выражения:
Примеры. Освободиться от иррациональности в знаменателе дроби:
1) ;
2) .
4, 5 и 6 группы – учащиеся со способностями выше средних.
Если знаменатель дроби — сумма либо разность двух выражений, содержащих квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный радикал:
;
Примеры. Освободиться от иррациональности в знаменателе дроби:
1) ;
2) ;
3)
Работа в новых группах (4 группы по 6 человек, от каждой группы по 1 человеку).
Объяснение изученного материала членам новой группы. (взаимооценивание – прокомментировать объяснение материала учеником)
V. Проверка усвоения теоретического материала. На вопросы отвечают учащиеся, не объясняющие данную часть теоретического материала.
1) Как избавиться от иррациональности в знаменателе дроби, если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей?
2) Как избавиться от иррациональности в знаменателе дроби, если знаменатель дроби — сумма либо разность двух выражений, содержащих квадратный корень?
3) как избавиться от иррациональности в знаменателе дроби
а)
4) Как избавиться от иррациональности в знаменателе дроби
?
VI. Закрепление изученного материала. Проверочная самостоятельная работа.
№81 («Алгебра» 8 класс, А.Абылкасымова, И.Бекбоев, А.Абдиев, З,Жумагулова)
№170 (1,2,3,5,6) («Алгебра» 8 класс, А.Шыныбеков)
Критерии оценивания:
Уровень А – № 81 примеры 1-5 отметка «3»
Уровень В – № 81 примеры 6-8 и №170 примеры 5,6 отметка «4»
Уровень С – № 170 примеры 1-6 отметка «5»
(самооценивание, проверка по образцу в флипчарте)
VII. Домашнее задание.
№ 218
VIII. Рефлексия. «Телеграмма»
Каждому предлагается заполнить бланк телеграммы, получив при этом следующую инструкцию: «Что вы думаете о прошедшем занятии? Что было для вас важным? Чему вы научились? Что вам понравилось? Что осталось неясным? В каком направлении нам стоит продвигаться дальше? Напишите мне, пожалуйста, об этом короткое послание –телеграмму из 11 слов. Я хочу узнать ваше мнение для того, чтобы учитывать его в дальнейшей работе».
Итог урока.
infourok.ru
Избавление от иррациональности в знаменателе дроби
Избавление от иррациональности в знаменателе дроби.
Цель урока: создание условий для формирования умений, избавляться от иррациональности в знаменателе дроби, содержащие арифметические квадратные корни в ходе работы в группах сменного состава.
Задачи урока: проверить теоретическую подготовку учащихся, умение извлекать корень п-й степени из числа, формировать навыки правильного воспроизведения своих знаний и умений, развивать вычислительные навыки, воспитывать умение работать в парах и ответственности за общее дело.
Ход урока.
I. Организационный момент
II. Повторение ранее изученного
Вынести множитель из-под знака корня:
Внести множитель под знак корня:
3
Упростить:а) б) в)
(Проверка после проверки домашнего задания)
III. Проверка домашнего задания.
(самооценивание с помощью сигнальных карточек: зелёный - всё верно, красный – есть ошибка)
IV. Изучение нового материала. Работа в группах сменного состава.
Самостоятельно изучить материал, чтобы потом суметь объяснить его членам группы. Класс делится на 6 групп по 4 человека.
1, 2 и 3 группы – учащиеся со средними способностями
Как избавиться от иррациональности в знаменателе дроби? Рассмотрим общий случай и конкретные примеры.
Если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей, чтобы избавиться от иррациональности в знаменателе и числитель, и знаменатель дроби умножаем на квадратный корень из этого числа или выражения:
Примеры. Освободиться от иррациональности в знаменателе дроби:
1) ;
2) .
4, 5 и 6 группы – учащиеся со способностями выше средних.
Если знаменатель дроби — сумма либо разность двух выражений, содержащих квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный радикал:
;
Примеры. Освободиться от иррациональности в знаменателе дроби:
1) ;
2) ;
3)
Работа в новых группах (4 группы по 6 человек, от каждой группы по 1 человеку).
Объяснение изученного материала членам новой группы. (взаимооценивание – прокомментировать объяснение материала учеником)
V. Проверка усвоения теоретического материала. На вопросы отвечают учащиеся, не объясняющие данную часть теоретического материала.
1) Как избавиться от иррациональности в знаменателе дроби, если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей?
2) Как избавиться от иррациональности в знаменателе дроби, если знаменатель дроби — сумма либо разность двух выражений, содержащих квадратный корень?
3) как избавиться от иррациональности в знаменателе дроби
а)
4) Как избавиться от иррациональности в знаменателе дроби
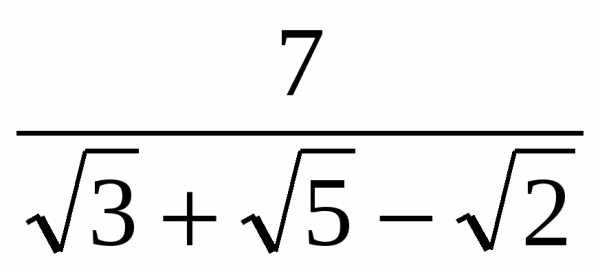 ?
?
VI. Закрепление изученного материала. Работа с учебником
VII. Домашнее задание.
VIII. Рефлексия. «Телеграмма»
Итог урока.
videouroki.net