Как найти синус, косинус и тангенс. Как найти синус через тангенс и косинус
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 | ||
| (2) | Основное тождество через тангенс и косинус | 1 + tg2(α) = 1/cos2(α) | ||
| (3) | Основное тождество через котангенс и синус | 1 + ctg2(α) = 1/sin2(α) | ||
| (4) | Соотношение между тангенсом и котангенсом | tg(α)ctg(α) = 1 | ||
| (5) | Синус двойного угла | sin(2α) = 2sin(α)cos(α) | ||
| (6) | Косинус двойного угла | cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α) | ||
| (7) | Тангенс двойного угла |
| ||
| (8) | Котангенс двойного угла |
| ||
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) | ||
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) | ||
| (11) | Косинус суммы/разности | cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) | ||
| (12) | Синус суммы/разности | sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) | ||
| (13) | Тангенс суммы/разности | tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β)) | ||
| (14) | Котангенс суммы/разности | ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β)) | ||
| (15) | Произведение синусов | sin(α)sin(β) = ½(cos(α–β) – cos(α+β)) | ||
| (16) | Произведение косинусов | cos(α)cos(β) = ½(cos(α+β) + cos(α–β)) | ||
| (17) | Произведение синуса на косинус | sin(α)cos(β) = ½(sin(α+β) + sin(α–β)) | ||
| (18) | Сумма/разность синусов | sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) | ||
| (19) | Сумма косинусов | cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β)) | ||
| (20) | Разность косинусов | cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β)) | ||
| (21) | Сумма/разность тангенсов | tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β) | ||
| (22) | Формула понижения степени синуса | sin2(α) = ½(1 – cos(2α)) | ||
| (23) | Формула понижения степени косинуса | cos2(α) = ½(1 + cos(2α)) | ||
| (24) | Сумма/разность синуса и косинуса | sin(α) ± cos(α) = &sqrt;2sin(α±π/4) | ||
| (25) | Сумма/разность синуса и косинуса с коэффициентами | Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²))) | ||
| (26) | Основное соотношение арксинуса и арккосинуса | arcsin(x) + arccos(x) = π/2 | ||
| (27) | Основное соотношение арктангенса и арккотангенса | arctg(x) + arcctg(x) = π/2 |
scolaire.ru
Основные формулы тригонометрии | umath.ru
1. Определения синуса, косинуса, тангенса и котангенса угла.
Синус угла (обозначается ) – ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинус угла (обозначается ) – абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенс угла (обозначается ) – отношение синуса угла к его косинусу, т.е.
Котангенс угла (обозначается ) – отношение косинуса угла к его синусу, т.е. 2. Основное тригонометрическое тождество: 3. Зависимость между синусом, косинусом, тангенсом и котангенсом: 4. Чётность, нечётность и периодичность тригонометрических функций.Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента :
Синус и косинус – периодические с периодом 2\pi функции, а тангенс и котангенс – периодические с периодом функции:Число является наименьшим положительным периодом синуса и косинуса, а число – наименьшим положительным периодом тангенса и котангенса. Для любого целого справедливы равенства 5. Формулы сложения: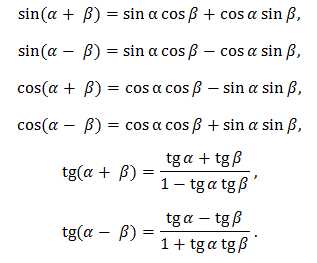
umath.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике - Тригонометрия
| Справочник по математике | Тригонометрия |
| Связи между тригонометрическими функциями одного угла |
| Тригонометрические функции суммы и разности двух углов |
| Тригонометрические функции двойного угла |
| Формулы понижения степени для квадратов тригонометрических функций |
| Формулы понижения степени для кубов синуса и косинуса |
| Выражение тангенса угла через синус и косинус двойного угла |
| Преобразование суммы тригонометрических функций в произведение |
| Преобразование произведения тригонометрических функций в сумму |
| Выражение тригонометрических функций через тангенс половинного угла |
| Тригонометрические функции тройного угла |
Связи между тригонометрическими функциями одного угла
| sin2α + cos2α = 1 |
Тригонометрические функции суммы и разности двух углов
| Формула | Название формулы |
| sin (α + β) = sin α cos β + cos α sin β | Синус суммы |
| sin (α – β) = sin α cos β – cos α sin β | Синус разности |
| cos (α + β) = cos α cos β – sin α sin β | Косинус суммы |
| cos (α – β) = cos α cos β + sin α sin β | Косинус разности |
| Тангенс суммы | |
| Тангенс разности |
| Синус суммы |
| sin (α + β) = sin α cos β ++ cos α sin β |
| Синус разности |
| sin (α – β) = sin α cos β –– cos α sin β |
| Косинус суммы |
| cos (α + β) = cos α cos β –– sin α sin β |
| Косинус разности |
| cos (α – β) = cos α cos β ++ sin α sin β |
| Тангенс суммы |
| Тангенс разности |
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α | Косинус двойного угла |
| Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
| Выражение квадрата синусачерез косинус двойного угла | |
| Выражение квадрата косинусачерез косинус двойного угла | |
| Выражение квадрата тангенсачерез косинус двойного угла |
| Выражение квадрата синуса через косинус двойного угла |
| Выражение квадрата косинуса через косинус двойного угла |
| Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
| Выражение куба синуса черезсинус угла и синус тройного угла | |
| Выражение куба косинуса черезкосинус угла и косинус тройного угла |
| Выражение куба синуса черезсинус угла и синус тройного угла |
| Выражение куба косинуса черезкосинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
| Формула | Название формулы |
| Сумма синусов | |
| Разность синусов | |
| Сумма косинусов | |
| Разность косинусов | |
| Сумма тангенсов | |
| Разность тангенсов |
| Сумма синусов |
| Разность синусов |
| Сумма косинусов |
| Разность косинусов |
| Сумма тангенсов |
| Разность тангенсов |
Преобразование произведения тригонометрических функций в сумму
| Формула | Название формулы |
| Произведение синусов | |
| Произведение косинусов | |
| Произведение синуса и косинуса |
| Произведение синусов |
| Произведение косинусов |
| Произведение синуса и косинуса |
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
| Выражение синуса угла черезтангенс половинного угла | |
| Выражение косинуса угла черезтангенс половинного угла | |
| Выражение тангенса угла черезтангенс половинного угла |
| Выражение синуса угла через тангенс половинного угла |
| Выражение косинуса угла через тангенс половинного угла |
| Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
| Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
| подготовительные курсы для школьников 10 и 11 классов |
У нас также для школьников организованы
| индивидуальные занятия с репетиторами по математике и русскому языку |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Онлайн калькулятор: Тригонометрические функции
 Простейшие тригонометрические функции
Простейшие тригонометрические функции Тригонометрические функции — вид элементарных функций, к которым относятся следующие функции:sin — синусcos — косинусtg — тангенсctg — котангенсsec — секансcosec — косекансversin — версинус (синус-верзус)vercos — коверсинус (косинус-верзус)haversin — гаверсинус (половина от синус-верзус)exsec — экссекансexcsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.
Единицы измерения Точность вычисленияЗнаков после запятой: 10
Значение тригонометрических функций
Сохранить share extension
Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:Тангенс: (отношение длины противоположного углу катета к прилежащему катету)Котангенс: (отношение длины прилежащего к углу катета к противоположному катету)Секанс: (отношение длины гипотенузы к прилежащему к углу катету)Косеканс: (отношение длины гипотенузы к противоположному катету)
Редко используемые тригонометрические функции:
Версинус:
Коверсинус:
Гаверсинус:
Экссеканс:
Экскосеканс:
planetcalc.ru
Как найти синус, косинус и тангенс
Синус, косинус и тангенс являются тригонометрическими функциями. Исторически они возникли как соотношения между сторонами прямоугольного треугольника, поэтому удобнее всего и вычислять их через прямоугольный треугольник. Однако через него можно выразить только тригонометрические функции острых углов. Для тупых углов придется вводить окружность.Вам понадобится
- окружность, прямоугольный треугольник
Инструкция
- Пусть в прямоугольном треугольнике угол B - прямой. AC будет являться гипотенузой этого треугольника, стороны AB и BC - его катетами. Синусом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к гипотенузе AC. То есть sin(BAC) = BC/AC.Косинусом острого угла BAC будет называться отношение прилежащего к этому углу катета BC к гипотенузе AC. То есть cos(BAC) = AB/AC. Косинус угла можно также выразить через синус угла с помощью основного тригонометрического тождества: ((sin(ABC))^2)+((cos(ABC))^2) = 1. Тогда cos(ABC) = sqrt(1-(sin(ABC))^2).Тангенсом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к прилежащему к этому углу катету AB. То есть tg(BAC) = BC/AB. Тангенс угла также можно выразить через его синус и косинус по формуле: tg(BAC) = sin(BAC)/cos(BAC).
- В прямоугольных треугольниках можно рассматривать только острые углы. Для рассмотрения прямых углов необходимо вводить окружность.Пусть O - центр декартовой системы координат с осями X (ось абцисс) и Y (ось ординат), а также центр окружности радиуса R. Отрезок OB будет являться радиусом этой окружности. Углы можно измерить как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначьте за xB, ординату - за yB.Тогда синус угла определяется как yB/R, косинус угла - xB/R, тангенс угла tg(x) = sin(x)/cos(x) = yB/xB.
- Косинус угла можно рассчитать и в любом треугольнике, если известны длины всех его сторон. По теореме косинусов AB^2 = ((AC)^2)+((BC)^2)-2*AC*BC*cos(ACB). Отсюда, cos(ACB) = ((AC^2)+(BC^2)-(AB^2))/(2*AC*BC).Синус и тангенс этого угла можно вычислить из приведенных выше определения тангенса угла и основного тригонометрического тождества.
completerepair.ru
Как найти синус, косинус и тангенс
Синус, косинус и тангенс являются тригонометрическими функциями. Исторически они появились как соотношения между сторонами прямоугольного треугольника, следственно комфортнее каждого и вычислять их через прямоугольный треугольник. Впрочем через него дозволено выразить только тригонометрические функции острых углов. Для тупых углов придется вводить окружность.

Вам понадобится
- окружность, прямоугольный треугольник
Инструкция
1. Пускай в прямоугольном треугольнике угол B — прямой. AC будет являться гипотенузой этого треугольника, стороны AB и BC — его катетами. Синусом острого угла BAC будет именоваться отношение противолежащего к этому углу катета BC к гипотенузе AC. То есть sin(BAC) = BC/AC.Косинусом острого угла BAC будет именоваться отношение прилежащего к этому углу катета BC к гипотенузе AC. То есть cos(BAC) = AB/AC. Косинус угла дозволено также выразить через синус угла с подмогой основного тригонометрического тождества: ((sin(ABC))^2)+((cos(ABC))^2) = 1. Тогда cos(ABC) = sqrt(1-(sin(ABC))^2).Тангенсом острого угла BAC будет именоваться отношение противолежащего к этому углу катета BC к прилежащему к этому углу катету AB. То есть tg(BAC) = BC/AB. Тангенс угла также дозволено выразить через его синус и косинус по формуле: tg(BAC) = sin(BAC)/cos(BAC).
2. В прямоугольных треугольниках дозволено рассматривать только острые углы. Для рассмотрения прямых углов нужно вводить окружность.Пускай O — центр декартовой системы координат с осями X (ось абцисс) и Y (ось ординат), а также центр окружности радиуса R. Отрезок OB будет являться радиусом этой окружности. Углы дозволено измерить как повороты от позитивного направления оси абсцисс до луча OB. Направление супротив часовой стрелки считается позитивным, по часовой стрелке негативным. Абсциссу точки В обозначьте за xB, ординату — за yB.Тогда синус угла определяется как yB/R, косинус угла — xB/R, тангенс угла tg(x) = sin(x)/cos(x) = yB/xB.
3. Косинус угла дозволено рассчитать и в любом треугольнике, если вестимы длины всех его сторон. По теореме косинусов AB^2 = ((AC)^2)+((BC)^2)-2*AC*BC*cos(ACB). Отсель, cos(ACB) = ((AC^2)+(BC^2)-(AB^2))/(2*AC*BC).Синус и тангенс этого угла дозволено вычислить из приведенных выше определения тангенса угла и основного тригонометрического тождества.
jprosto.ru
Как найти синус, косинус и тангенс
Синус, косинус и тангенс являются тригонометрическими функциями. Исторически они возникли как соотношения между сторонами прямоугольного треугольника, поэтому удобнее всего и вычислять их через прямоугольный треугольник. Однако через него можно выразить только тригонометрические функции острых углов. Для тупых углов придется вводить окружность.
Вам понадобитсяокружность, прямоугольный треугольник
Спонсор размещения P&G Статьи по теме "Как найти синус, косинус и тангенс" Как решать тригонометрические функции Как вычислить сторону треугольника Как найти тангенс, если известен косинусИнструкция
1
Пусть в прямоугольном треугольнике угол B - прямой. AC будет являться гипотенузой этого треугольника, стороны AB и BC - его катетами. Синусом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к гипотенузе AC. То есть sin(BAC) = BC/AC.
Косинусом острого угла BAC будет называться отношение прилежащего к этому углу катета BC к гипотенузе AC. То есть cos(BAC) = AB/AC. Косинус угла можно также выразить через синус угла с помощью основного тригонометрического тождества: ((sin(ABC))^2)+((cos(ABC))^2) = 1. Тогда cos(ABC) = sqrt(1-(sin(ABC))^2).
Тангенсом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к прилежащему к этому углу катету AB. То есть tg(BAC) = BC/AB. Тангенс угла также можно выразить через его синус и косинус по формуле: tg(BAC) = sin(BAC)/cos(BAC).
2
В прямоугольных треугольниках можно рассматривать только острые углы. Для рассмотрения прямых углов необходимо вводить окружность.
Пусть O - центр декартовой системы координат с осями X (ось абцисс) и Y (ось ординат), а также центр окружности радиуса R. Отрезок OB будет являться радиусом этой окружности. Углы можно измерить как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначьте за xB, ординату - за yB.
Тогда синус угла определяется как yB/R, косинус угла - xB/R, тангенс угла tg(x) = sin(x)/cos(x) = yB/xB.
3
Косинус угла можно рассчитать и в любом треугольнике, если известны длины всех его сторон. По теореме косинусов AB^2 = ((AC)^2)+((BC)^2)-2*AC*BC*cos(ACB). Отсюда, cos(ACB) = ((AC^2)+(BC^2)-(AB^2))/(2*AC*BC).
Синус и тангенс этого угла можно вычислить из приведенных выше определения тангенса угла и основного тригонометрического тождества.
Как простоmasterotvetov.com