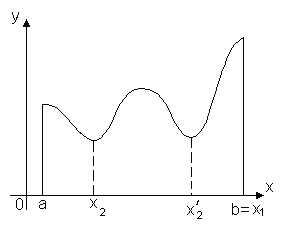
Прямоугольная и равнобедренная трапеция: свойства и признаки. Как найти высоту в равнобедренной трапеции если известны основания
Все формулы высоты равнобедренной трапеции
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
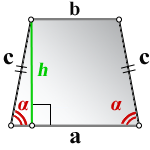
a - нижнее основание
b - верхнее основание
c - равные боковые стороны
α - угол при нижнем основании
h - высота трапеции
Формулы длины высоты, (h ):

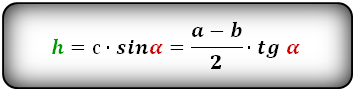
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
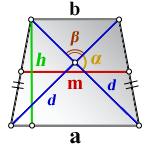
d - диагонали трапеции
α , β - углы между диагоналями
a , b - основания
h - высота трапеции
m - средняя линия
Формулы длины высоты, (h ):
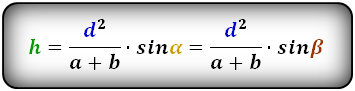
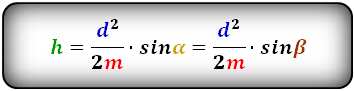
3. Формула высоты равнобедренной трапеции через площадь
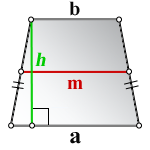
S - площадь трапеции
a , b - основания
h - высота трапеции
m - средняя линия
Формулы длины высоты, (h ):
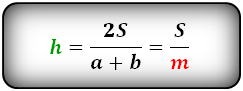
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Как найти высоту равнобедренной трапеции
Использование геометрии на практике, исключительно в строительстве видимо. Трапеция одна из особенно зачастую встречающихся геометрических фигур, точность расчета элементов которой — залог красоты строящегося объекта.
Вам понадобится
Инструкция
1. Трапеция представляет собой четырехугольник, две стороны которого параллельны — основания, а две другие не параллельны – боковые стороны. Трапеция, боковые стороны которой равны, именуется равнобедренной либо равнобочной. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований, мы разглядим случай, когда диагонали не перпендикулярны.
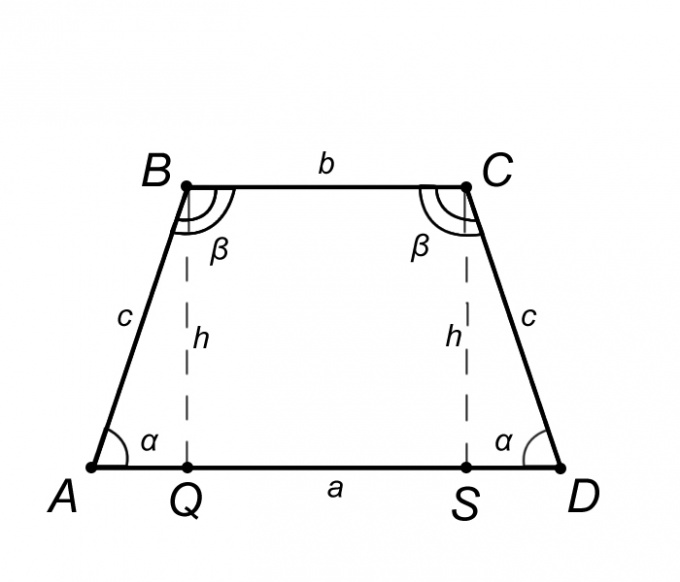
2. Разглядим равнобедренную трапецию ABCD и опишем ее свойства, но лишь те из них, умение которых поможет нам решить поставленную задачу. Из определения равнобедренной трапеции основание AD = a параллельно BC = b, а боковая сторона AB = CD = c из этого следует, что углы при основаниях равны, то есть угол BAQ = CDS = ?, таким же образом угол ABC = BCD = ?. Обобщив вышесказанное, объективно утверждать, что треугольник ABQ равен треугольнику SCD, а значит, отрезок AQ = SD = (AD – BC)/2 = (a – b)/2.
3. Если в условии задачи нам даны длины оснований a и b, а также длина боковой стороны с, то высота трапеции h, равная отрезку BQ, находится дальнейшим образом. Разглядим треугольник ABQ, потому что по определению высота трапеции есть перпендикуляр к основанию, то дозволено утверждать, что треугольник ABQ прямоугольный. Сторона AQ треугольника ABQ, исходя из свойств равнобедренной трапеции, находится по формуле AQ = (a – b)/2. Сейчас зная две стороны AQ и c, по теореме Пифагора находим высоту h. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов катетов. Запишем эту теорему применительно к нашей задаче: c^2=AQ^2+ h^2. Отсель следует, что h = ?(c^2-AQ^2).
4. Для примера разглядим трапецию ABCD, в которой основания AD = a = 10см BC = b = 4см, боковая сторона AB = c = 12см. Обнаружить высоту трапеции h. Находим сторону AQ треугольника ABQ. AQ = (a – b)/2 = (10-4)/2=3см. Дальше подставляем значения сторон треугольника в теорему Пифагора. h = ?(c^2-AQ^2) = ?(12^2-3^2) =?135=11.6см.
Трапецией считается такой четырехугольник, у которого две стороны параллельны, а две другие нет. Высотой трапеции именуется отрезок, проведенный перпендикулярно между двумя параллельными прямыми. В зависимости от начальных данных ее дозволено вычислить по-различному.
Вам понадобится
- Знание сторон, оснований, средней линии трапеции, а так же, опционально, ее площадь и/или периметр.
Инструкция
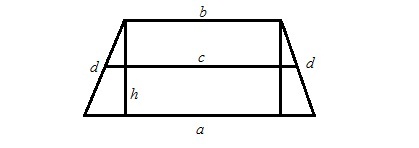
1. Одним из методов вычислить площадь трапеции является произведение высоты и средней линии. Возможен, что имеется равнобедренная трапеция. Тогда высота равнобедренной трапеции с основаниями a и b, площадью S и периметром P будет рассчитана так:h=2 х S/(P-2 х d). (см. рис 1)
2. Если вестима только площадь трапеции и ее основания, то формулу расчета высоты дозволено вывести из формулы площади трапеции S = 1/2h x (a+b):h = 2S/(a+b).
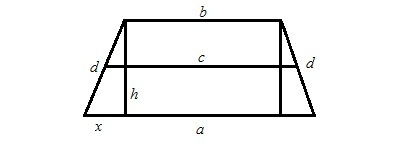
3. Возможен, имеется трапеция с теми же данными, что и на рисунке 1. Проведем 2 высоты, получим прямоугольник, у которого 2 меньшие стороны являются катетами прямоугольных треугольников. Обозначим меньший катит за x. Он находится путем деления разницы длин между огромным и меньшим основаниями. Тогда по теореме Пифагора квадрат высоты равен сумме квадратов гипотенузы d и катета x. Извлекаем корень из этой суммы и получим высоту h. (рис. 2)
Видео по теме
Равнобедренная трапеция — это трапеция, у которой противолежащие непараллельные стороны равны. Ряд формул дозволяют обнаружить площадь трапеции через ее стороны, углы, высоту и.т.д. Для случая равнобедренных трапеций эти формулы могут несколько упрощаться.
Инструкция
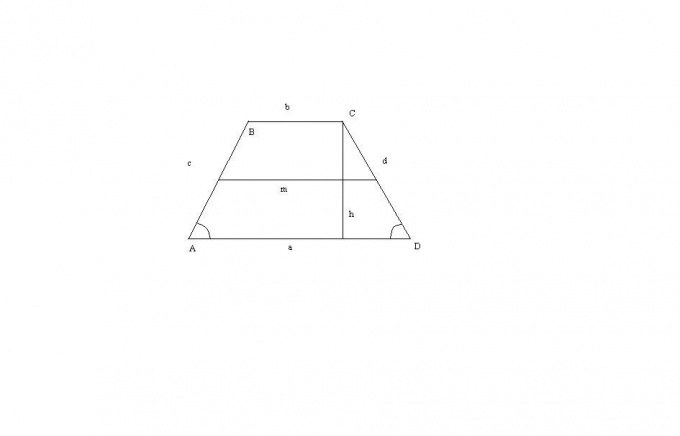
1. Четырехугольник, у которого пара противолежащих сторон параллельна, называют трапецией. В трапеции определяют основания, стороны, диагонали, высоту, среднюю линию. Зная разные элементы трапеции, дозволено обнаружить ее площадь.
2. Изредка особыми случаями равнобедренных трапеций считаются прямоугольники и квадраты, но во многих источниках они к трапециям не относятся. Еще одним особым случаем равнобедренной трапеции считается такая геометрическая фигура с 3 равными сторона. Ее называют трехсторонней трапецией, либо триравнобедренной трапецией, либо, реже, symtra. Такую трапецию дозволено рассматривать как отсечение 4 последовательных вершин от положительного многоугольника, имеющего 5 либо больше сторон.
3. Трапеция состоит из оснований (параллельные противоположные стороны), боковых сторон (две другие стороны), средней линии (отрезок, соединяющий середины боковых сторон). Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
4. Дабы трапеция считалась равнобедренной, должно выполняться как минимум одно из следующих условий. Первое: углы при основе трапеции обязаны быть равны: ?ABC = ?BCD и ?BAD = ?ADC. Второе: диагонали трапеции обязаны быть равны: AC = BD. Третье: если углы между диагоналями и основаниями идентичны, трапеция считается равнобедренной: ?ABD = ?ACD, ?DBC = ?ACB, ?CAD = ?ADB, ?BAC = ?BDC. Четвертое: сумма противоположных углов равна 180°: ?ABC + ?ADC = 180° и ?BAD + ?BCD = 180°. Пятое: если вокруг трапеции дозволено описать окружность, она считается равнобедренной.
5. Равнобедренная трапеция, как и любая иная геометрическая фигура, владеет рядом постоянных свойств. Первое из них: сумма углов, прилегающих к боковой стороне равнобедренной трапеции равна 180°: ?ABC + ?BAD = 180° и ?ADC + ?BCD = 180°. Второе: если в равнобедренную трапецию дозволено вписать окружность, то ее боковая сторона равна средней линии трапеции: AB = CD = m. Третье: вокруг равнобедренной трапеции неизменно дозволено описать окружность. Четвертое: если диагонали взаимно перпендикулярны, то высота трапеции равна полусумме оснований (средней линии): h=m. Пятое: если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты: SABCD = h3 . Шестое: если в равнобедренную трапецию дозволено вписать окружность, то квадрат высоты равен произведению основ трапеции: h3 = BC • AD. Седьмое: сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции: AC2 + BD2 = AB2 + CD2 + 2BC • AD. Восьмое: прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции: HF ? BC ? AD. Девятое: высота ((CP), опущенная из вершины (C) на большее основание (AD), делит его на огромный отрезок (AP), тот, что равен полусумме оснований и меньшый (PD) — равен полуразности оснований: AP=BC+AD/2, PD=AD-BC/2.
6. Самая распространенная формула для вычисления площади трапеции — S = (a+b)h/2. Для случая равнобедренной трапеции она очевидным образом не поменяется. Дозволено лишь подметить, что у равнобедренной трапеции углы при любом из оснований будут равны (DAB = CDA = x). Потому что ее боковые стороны тоже равны (AB = CD = с), то и высоту h дозволено посчитать по формуле h = с*sin(x).Тогда S = (a+b)*с*sin(x)/2.Подобно, площадь трапеции дозволено записать через среднюю сторону трапеции: S = mh.
7. Разглядим частный случай равнобедренной трапеции, когда ее диагонали перпендикулярны. В этом случае, по свойству трапеции, ее высота равна полусумме оснований.Тогда площадь трапеции дозволено вычислить по формуле: S = (a+b)^2/4.
8. Разглядим также еще одну формулу для определения площади трапеции: S = ((a+b)/2)*sqrt(c^2 — ((b-a)^2+c^2-d^2)/2(b-a))^2), где c и d — боковые стороны трапеции. Тогда в случае равнобедренной трапеции, когда c = d, формула принимает вид: S = ((a+b)/2)*sqrt(c^2-((b-a)^2/2(b-a))^2).
9. Обнаружьте площадь трапеции по формуле S=0,5?(a+b)?h, если знамениты a и b — длины оснований трапеции, то есть параллельные стороны четырехугольника, и h — высота трапеции (наименьшее расстояние между основаниями). Скажем, пускай дана трапеция с основаниями a=3 см, b=4 см и высотой h=7 см. Тогда ее площадь будет равна S=0,5?(3+4)?7=24,5 см?.
10. Воспользуйтесь дальнейшей формулой для вычисления площади трапеции: S=0,5?AC?BD?sin(?), где AC и BD — диагонали трапеции, а ? — угол между этими диагоналями. Скажем, задана трапеция с диагоналями AC=4 см и BD=6 см и углом ?=52°, тогда sin(52°)?0,79. Подставьте значения в формулу S=0,5?4?6?0,79?9,5 см?.
11. Посчитайте площадь трапеции, когда вестимы ее m — средняя линия (отрезок, соединяющий середины сторон трапеции) и h — высота. В этом случае площадь будет равна S=m?h. К примеру, пускай у трапеции средняя линия m=10 см, а высота h=4 см. В этом случае получается, что площадь заданной трапеции равна S=10?4=40 см?.
12. Вычислите площадь трапеции, в случае когда даны длины ее боковых сторон и оснований по формуле: S=0,5?(a+b)??(c??(((b?a)?+c??d?)?(2?(b?a)))?), где a и b — основания трапеции, а c и d — ее боковые стороны. Скажем, пускай дана трапеция с основаниями 40 см и 14 см и боковыми сторонами 17 см и 25 см. По вышеуказанной формуле S=0,5?(40+14)??(17??(((14?40)?+17??25?)?(2?(14?40)))?)?423,7 см?.
13. Рассчитайте площадь равнобедренной (равнобокой) трапеции, то есть трапеции у которой боковые стороны равны, если в нее вписана окружность по формуле: S=(4?r?)?sin(?), где r — радиус вписанной окружности, ? — угол при основании трапеции. В равнобедренной трапеции углы при основании равны. Скажем, пускай в трапецию вписана окружность радиусом r=3 см, а угол при основании ?=30°, тогда sin(30°)=0,5. Подставьте значения в формулу: S=(4?3?)?0,5=72 см?.
Трапеция, в которой длины боковых сторон равны, а основания параллельны, именуется равнобедренной либо равнобокой. Обе диагонали в такой геометрической фигуре имеют идентичную длину, которую в зависимости от вестимых параметров трапеции дозволено рассчитать различными методами.
Инструкция
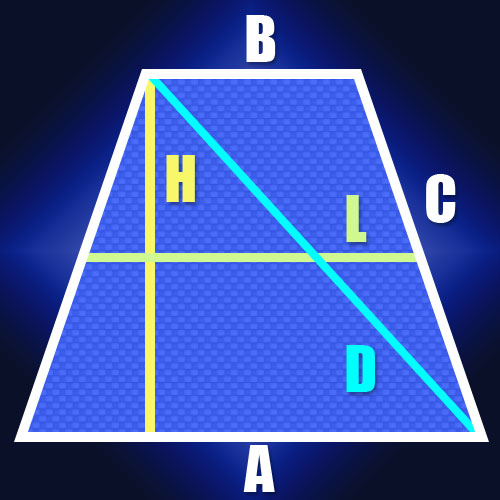
1. Если знамениты длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) дозволено воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей. Это качество вытекает из того факта, что всякая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Потому что боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это качество дозволено записать в таком виде: A? + B? + 2C? = 2D?. Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A? + B?)/2 + C?).
2. Если длины сторон не знамениты, но есть длина средней линии (L) и высота (H) равнобедренной трапеции, то длину диагонали (D) тоже вычислить нетрудно. Потому что длина средней линии равна полусумме оснований трапеции, то это дает вероятность обнаружить длину отрезка между точкой на большем основании, в которую опущена высота, и вершиной, прилегающей к этому основанию. В равнобедренной трапеции длина этого отрезка будет совпадать с длиной средней линии. Потому что диагональ замыкает данный отрезок и высоту трапеции в прямоугольный треугольник, то вычислить ее длину не составит труда. Скажем, по той же самой теореме Пифагора она будет равна квадратному корню из суммы квадратов высоты и средней линии: D=√(L? + H?).
3. Если знамениты длины обоих оснований равнобедренной трапеции (A и B) и ее высота (H), то, как и в предыдущем случае, дозволено вычислить длину отрезка между точкой, опущенной на огромную сторону высоты и прилегающей к ней вершиной. Формула из предыдущего шага трансформируется к такому виду: D=√((A + B)?/4 + H?).
Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Эти стороны именуются основаниями. Их финальные точки объединены отрезками, которые именуются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.

Вам понадобится
- — равнобедренная трапеция;
- — длины оснований трапеции;
- — высота трапеции;
- — лист бумаги;
- — карандаш;
- — линейка.
Инструкция
1. Постройте трапецию согласно условиям задачи. Вам обязаны быть даны несколько параметров. Как водится, это оба основания и высота. Но допустимы и другие данные — одно из оснований, его наклона к нему боковой стороны и высота. Обозначьте трапецию как АBCD, основания пускай будут a и b, высоту обозначьте как h, а боковые стороны — х. От того что трапеция равнобедренная, боковые стороны у нее равны.
2. Из вершин B и С проведите высоты к нижнему основанию. Точки пересечения обозначьте как M и N. К вас получилось два прямоугольных треугольника — AМВ и СND. Они равны, от того что по условиям задачи равны их гипотенузы АВ и CD, а также катеты ВМ и СN. Соответственно, отрезки АМ и DN также равны между собой. Обозначьте их длину как y.
3. Для того, дабы обнаружить длину суммы этих отрезков, нужно из длины основания a вычесть длину основания b. 2у=a-b. Соответственно, один такой отрезок будет равен разности оснований, деленной на 2. y=(a-b)/2.
4. Обнаружьте длину боковой стороны трапеции, которая единовременно является и гипотенузой прямоугольного треугольника с вестимыми вам катетами. Вычислите ее по теореме Пифагора. Она будет равна квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=?y2+h3=?(a-b)2/4+h3.
5. Зная высоту и угол наклона боковой стороны к основанию, сделайте те же самые построения. Разность оснований в этом случае вычислять не необходимо. Воспользуйтесь теоремой синусов. Гипотенуза равна длине катета, умноженной на синус противолежащего ему угла. В данном случае x=h*sinCDN либо x=h*sinBAM.
6. Если вам дан угол наклона боковой стороны трапеции не к нижнему, а к верхнему основанию, обнаружьте надобный угол, исходя из свойства параллельных прямых. Припомните одно из свойств равнобедренной трапеции, согласно которому углы между одним из оснований и боковыми сторонами равны.
Обратите внимание! Повторите свойства равнобедренной трапеции. Если поделить оба ее основания напополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Скажем, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а иной — половине их разности.
Трапецией считают четырехугольник, имеющий лишь две параллельные стороны — они именуются основаниями этой фигуры. Если при этом длины 2-х других — боковых — сторон идентичны, трапеция именуется равнобедренной либо равнобокой. Линия, которая соединяет середины боковых сторон, именуется средней линией трапеции и может быть рассчитана несколькими методами.
Инструкция
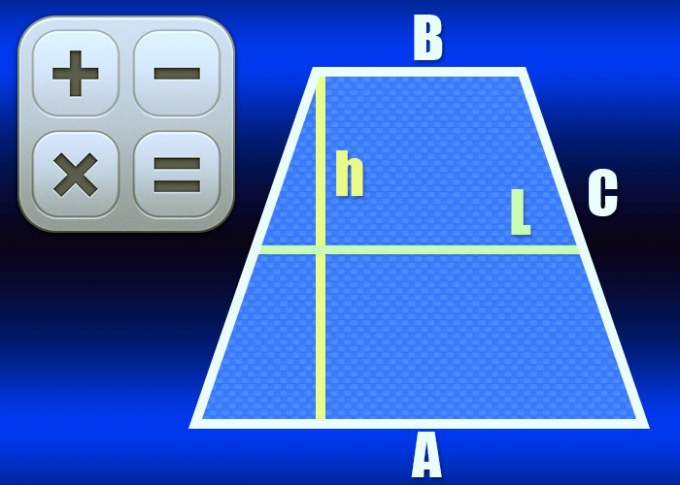
1. Если вестимы длины обоих оснований (А и В), для вычисления длины средней линии (L) используйте основное качество этого элемента равнобедренной трапеции — она равна полусумме длин оснований: L = ?*(А+В). Скажем, в трапеции с основаниями, имеющими длины 10см и 20см, средняя линия должна быть равна ?*(10+20) = 15см.
2. Средняя линия (L) совместно с высотой (h) равнобокой трапеции является сомножителем в формуле вычисления площади (S) этой фигуры. Если эти два параметра даны в начальных условиях задачи, для вычисления длины средней линии разделяете площадь на высоту: L = S/h. Скажем, при площади в 75 см? равнобедренная трапеция высотой в 15см должна иметь среднюю линию длиной в 75/15 = 5см.
3. При вестимых периметре (Р) и длине боковой стороны (С) равнобедренной трапеции рассчитать среднюю линию (L) фигуры тоже нетрудно. Отнимите от периметра две длины боковых сторон, а оставшаяся величина будет суммой длин оснований — поделите ее напополам, и задача будет решена: L = (P-2*С)/2. Скажем, при периметре, равном 150см, и боковой стороне длиной в 25см длина средней линии должна составить (150-2*25)/2 = 50см.
4. Зная длины периметра (P) и высоты (h), а также величину одного из острых углов (?) равнобедренной трапеции, тоже дозволено вычислить длину ее средней линии (L). В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина иного знаменита. Это дозволит вычислить длину боковой стороны по теореме синусов — поделите высоту на синус вестимого угла: h/sin(?). После этого подставьте это выражение в формулу из предыдущего шага и вы получите такое равенство: L = (P-2*h/sin(?))/2 = P/2-h/sin(?). Скажем, если знаменитый угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
Трапецией называют четырехугольник, основания которого лежат на 2-х параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
Инструкция
1. У равнобедренной (либо равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
2. Трапеция имеет два основания, и дабы их обнаружить, надобно вначале обозначить фигуру. Пускай дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом знамениты все параметры, помимо оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
3. Для решения задачи об основании трапеции проще каждого будет составить систему уравнений, дабы через взаимосвязанные величины обнаружить надобные основания.
4. Обозначьте отрезок BC за x, а AD за y, дабы в будущем было комфортно обращаться с формулами и понимать их. Если не сделать этого сразу, дозволено запутаться.
5. Выпишите все формулы, которые сгодятся при решении поставленной задачи, применяя вестимые данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
6. Припомните качество равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсель следует, что два основания дозволено связать по формуле, вытекающей из этого свойства: AD=BC+2AH либо y=x+2AH
7. Обнаружьте катет AH, следуя теореме Пифагора, которую вы теснее записали. Пускай он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
8. Выразите через площадь трапеции незнакомую величину. У вас должно получиться: AD=2*S/h-BC либо y=2*S/h-x.
9. Позже этого подставьте данные числовые значения в полученную систему уравнений и решите ее. Решение всякий системы уравнений дозволено обнаружить механически в программе MathCAD.
Полезный совет Усердствуйте неизменно при решении задач максимально упростить обозначения и формулы. Так решение найдется значительно стремительней.
Полезный совет Свойства равнобедренной трапеции.Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, иной — полуразности оснований.В равнобедренной трапеции углы при любом основании равны.В равнобедренной трапеции длины диагоналей равны.Около равнобедренной трапеции дозволено описать окружность.Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
jprosto.ru
Найдите высоту трапеции, если даны основания и боковая сторона – как решать
Формулировка задачи: Основания равнобедренной трапеции равны a и b, боковая сторона равна c. Найдите высоту трапеции.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:
Основания равнобедренной трапеции равны 10 и 24, боковая сторона равна 25. Найдите высоту трапеции.
Решение:
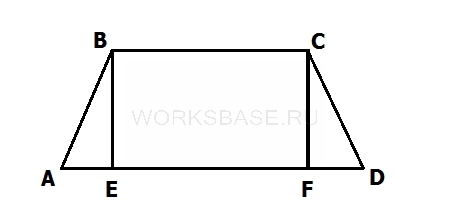
Рассмотрим равнобедренную трапецию ABCD, в котором нужно найти высоту BE:
BC = 10
AD = 24
AB = CD = 25
Для решения задачи можно перейти к прямоугольному треугольнику △ABE, в котором известна сторона AB и можно найти сторону AE:
AE = (AD – BC) / 2 = (24 – 10) / 2 = 7
Теперь можно найти катет BE по теореме Пифагора:
BE = √AB2 – AE2 = √252 – 72 = √576 = 24
Ответ: 24
В общем виде решение данной задачи по планиметрии выглядит следующим образом:
ВЫСОТА ТРАПЕЦИИ = √c2 – ((b – a) / 2)2
где a – меньшее основание, b – большее основание, c – боковая сторона.
Остается лишь подставить конкретные значения и подсчитать результат.
Поделитесь статьей с одноклассниками «Найдите высоту трапеции, если даны основания и боковая сторона – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
worksbase.ru
Как найти высоту равнобедренной трапеции
Доброй ночи.Очень хорошо, что Вы обратились именно к нам. Я уверена, что мы сможем Вам помочь понять данную тему. Для начала я предлагаю разобраться с тем, что такое трапеция. Ведь, как я поняла, с пониманием данного понятия произошла проблема. Но на самом деле всё просто.Итак, трапеция — это четырёхугольник, у которого лишь две стороны параллельны. Эти стороны называются основаниями трапеции.А что ж такое равнобедренная трапеция? Равнобедренной называется такая трапеция, у которой боковые стороны равны.Высота же в свою очередь — это перпендикуляр, опущенный из вершины геометрической фигуры к основанию.Допустим нам дана равнобедренная трапеция ABCD. Нам известно, что её площадь равна 200 см квадратных. А средняя линия треугольника равна 50 см. Нам нужно понять, как найти высоту равнобедренной трапецииДавайте подумаем, как же мы можем выразить нашу высоту. Наиболее вероятно, учитывая, что мы знаем, сделать это из формулы площади трапеции:
![Rendered by QuickLaTeX.com \[S = m * h\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1458e57e634d3fdaa536e40468ea55d9_l3.png)
где 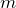 — средняя линия, а
— средняя линия, а 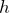 — высота трапеции.Теперь из этой формулы выразим с Вами высоту, которую нам и следует найти:
— высота трапеции.Теперь из этой формулы выразим с Вами высоту, которую нам и следует найти:
![Rendered by QuickLaTeX.com \[S = m * h\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1458e57e634d3fdaa536e40468ea55d9_l3.png)
![Rendered by QuickLaTeX.com \[h= \frac{S}{m}\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-87dc5392201a8a84aac46ab51bdb467c_l3.png)
И вот теперь мы можем подставить известные значения в получившиеся формулу:
![Rendered by QuickLaTeX.com \[h= \frac{200}{50}\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8abd2de6867adc06119f6f45468b9888_l3.png)
![Rendered by QuickLaTeX.com \[h= 4\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7915a97006978e971bca1a206e3e7bd9_l3.png)
Вот мы с Вами и справились.Ответ: 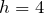 см
см
ru.solverbook.com
Все формулы высоты трапеции
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются - верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
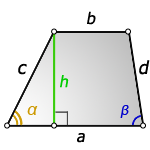
a - нижнее основание
b - верхнее основание
c , d - боковые стороны
α, β - углы трапеции
h - высота трапеции
Формулы длины высоты, (h ):
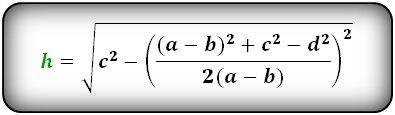
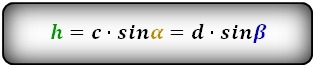
2. Формула высоты трапеции через диагонали и углы между ними
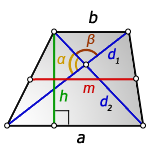
d1 , d2 - диагонали трапеции
α , β - углы между диагоналями
a , b - основания
h - высота трапеции
m - средняя линия
Формулы длины высоты, (h ):
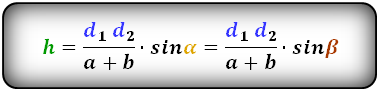
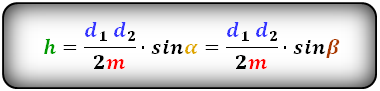
3. Формула высоты трапеции через площадь
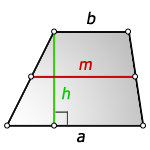
S - площадь трапеции
a , b - основания
h - высота трапеции
m - средняя линия
Формулы длины высоты, (h ):
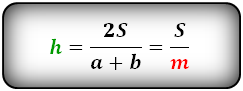
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
свойства и признаки: площадь, средняя линия прямоугольной, равнобедренной, как найти высоту

С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
...
Вконтакте
Google+
Мой мир
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые параллельны друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
 Если сложить все градусные меры внутренних углов, то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Если сложить все градусные меры внутренних углов, то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет высотой. Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить окружность.
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции:
- Если диагонали пересекаются под углом, то половина суммы оснований будет равна длине высоты.
- В случае, когда в правильную трапецию построена, или может быть построена, окружность, то квадрат высоты равен произведению величин оснований.
- Ось симметрии и средняя линия трапеции являются одним и тем же ГМТ.
- Когда диагонали пересекаются под прямым углом, тогда для вычисления площади потребуется формула:
- Окружность вписанная в трапецию, делает величину средней линии равной боковой.
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Решение:
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как:
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
uchim.guru
Высота равнобедренной трапеции | Треугольники
Это свойство равнобедренной трапеции удобно доказать в общем виде в начале изучения темы, чтобы в дальнейшем использовать его при решении задач.
Утверждение.
Высота равнобедренной трапеции, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
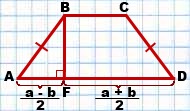 AD=a,
AD=a,
BC=b
![Rendered by QuickLaTeX.com \[AF = \frac{{a - b}}{2}\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-b3a70f52c2befcc450d4927a2556375c_l3.png)
![Rendered by QuickLaTeX.com \[DF = \frac{{a + b}}{2}\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3c0e2db760cf7061cefaa33ec17d259f_l3.png)
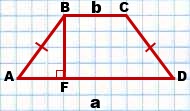 Дано: ABCD — трапеция,
Дано: ABCD — трапеция,
AD ∥ BC, AB=CD, AD>BC,
AD=a, BC=b,
![Rendered by QuickLaTeX.com \[BF \bot AD\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-fd6185a9a35cfd6707f3825bc183d5ab_l3.png)
Доказать:
![Rendered by QuickLaTeX.com \[AF = \frac{{a - b}}{2}\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-b3a70f52c2befcc450d4927a2556375c_l3.png)
![Rendered by QuickLaTeX.com \[DF = \frac{{a + b}}{2}\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3c0e2db760cf7061cefaa33ec17d259f_l3.png)
Доказательство:
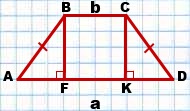 1) Проведем высоту CK:
1) Проведем высоту CK:
![Rendered by QuickLaTeX.com \[CK \bot AD,CK \bot BC.\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-bca6835522ca4dced4ca3a2e2c087d33_l3.png)
2) Четырехугольник ABCD — прямоугольник (так как у него все углы прямые). Следовательно, его противоположные стороны равны: FK=BC=b.
3) Рассмотрим треугольники ABF и DCK.
∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).
AB=CD (по условию),
BF=CK (как высоты трапеции).
Следовательно, треугольники ABF и DCK равны (по катету и гипотенузе).
Из равенства треугольников следует равенство соответствующих сторон:
![Rendered by QuickLaTeX.com \[AF = KD = \frac{{AD - FK}}{2} = \frac{{a - b}}{2}.\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-d575171ed04e270c6a757715fcf0535c_l3.png)
![Rendered by QuickLaTeX.com \[FD = FK + KD = {b^{\backslash 2}} + \frac{{a - b}}{2} = \]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-38e5b2999aa25642f4a1e6b4a7dac9a0_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{{2b + a - b}}{2} = \frac{{a + b}}{2}.\]](/800/600/http/www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-135f0bc2fa5ca74279e2a6ae89e387d0_l3.png)
Что и требовалось доказать.
Поскольку средняя линия трапеции равна полусумме ее оснований, длина отрезка FD равна длине среднее линии трапеции.
www.treugolniki.ru