Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7. Как построить касательную к графику функции
Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7
Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7.
Вспомним определение производной:
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Исходя из этого определения, рассмотрим, каким образом производная функции связана с графиком этой функции.
Посмотрите ВИДЕОУРОК, в котором я подробно объясняю, в чем заключается геометрический смысл производной, и как выводится уравнение касательной. А затем мы рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике.
Геометрический смысл производной.
Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции в точке равен производной функции в этой точке:
Заметим, что угол - это угол между прямой и положительным направлением оси ОХ:
Уравнение касательной к графику функции в точке имеет вид:
В этом уравнении:
- абсцисса точки касания,
- значение функции в точке касания,
- значение производной функции в точке касания.
Приведем несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике, в которых используется знание геометрического смысла производной.
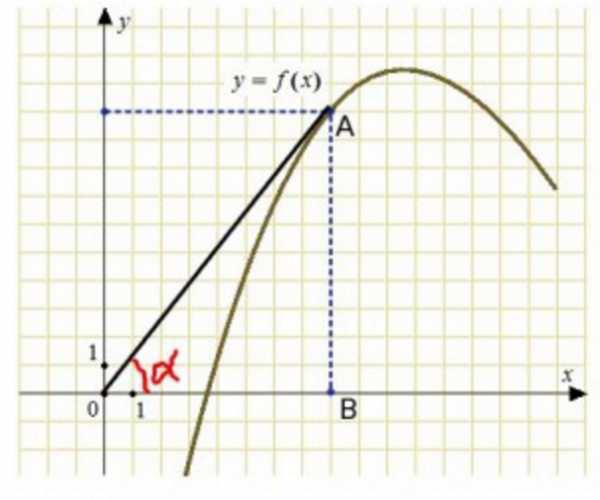
Пример 1. Задание В8 (№ 27504) На рисунке изображены график функции и касательная к нему в точке с абcцисcой . Найдите значение производной функции в точке .
Значение производной функции в точке равно тангенсу угла между касательной и положительным направлением оси ОХ. Чтобы его найти, выделим прямоугольный треугольник, гипотенуза которого лежит на касательной, а катеты параллельны осям координат. Обозначим точки с целыми координатами буквами А и В - эти точки выделены на касательной:
Проведем через точку А прямую параллельно оси ОХ, а через точку В - параллельно оси OY. Получим прямоугольный треугольник ABC:
Угол А треугольника АВС равен углу между касательной и положительным направлением оси ОХ.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Длины катетов считаем по количеству клеточек.
Ответ: 0,25
Пример 2. Задание В8 (№ 27506) На рисунке изображены график функции и касательная к нему в точке с абцисоой . Найдите значение производной функции в точке .
Эта задача очень похожа на предыдущую, за исключением того, что здесь касательная наклонена влево, и угол между касательной и положительным направлением оси ОХ расположен так:
Построим, как предыдущей задаче, прямоугольный треугольник АВС:
Угол А треугольника ABC и угол - смежные, то есть их сумма равна 180 градусов. Значит,
Запомните, если прямая наклонена влево, то коэффициент наклона прямой отрицателен.
Ответ: -0,25
Пример 3. Задание В8 (№ 40129) На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсцссой 8. Найдите значение производной функции в точке .
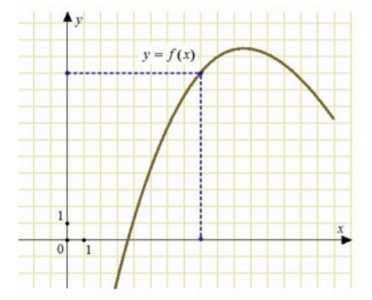
Соединим отрезком точку начала координат с точкой касания:
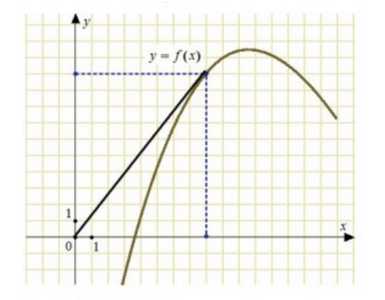
Производная функции в точке касания равна тангенсу угла между касательной и положительным направлением оси ОХ:
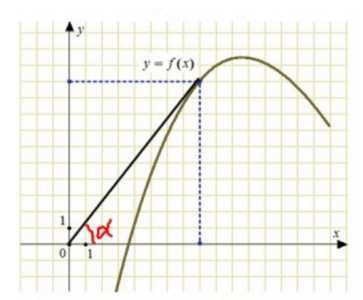
Чтобы найти тангенс , рассмотрим прямоугольный треугольник АОВ:
Ответ: 1,25
И.В. Фельдман, репетитор по математике.
ege-ok.ru
как составить и решить задачу с его помощью
Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Как составлять уравнение касательной в заданной точке
При написании уравнения будем использовать следующие обозначения:
- x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
- f(x) — исходная функция;
- f'(x) — производная от функции;
- k — угловой коэффициент.
Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.
Алгоритм написания уравнения
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:
- Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
- Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
- Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
- Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.
В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.
Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.
Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.
Задачи на написание уравнения касательной
Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.
Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.
Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.
- Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
- Возьмем от функции производную: f'(x) = 4x.
- Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
- Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
- Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.
В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.
Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).
- Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
- Запишем производную: g'(x) = 6x².
- Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
- Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
- Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
- В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.
Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.
Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.
Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.
Видео
Закрепить это тему вам поможет видео.
liveposts.ru
уравнение касательной - 24 Августа 2013 - Примеры решений задач
Тема: Как найти уравнение касательной к графику функции
Уравнение касательной к графику функции y=f(x) в точке x0 имеет вид
в точке x0=2.
Алгоритм решения следующий:
1) Находим производную функции
2) Вычисляем значение производной в точке x0=2 3) Вычисляем значение функции в точке x0=24) Найденные значения подставляем в формулу уравнения касательной
Получаем уравнение касательной
Для наглядности рекомендуем построить график самой функции и касательной на координатной плоскости с помощью калькулятора. Для этого вводим в калькулятор функцию в виде 3x^2-5x+1 и касательную в виде 7x-11, задаем интервал построения графиков от x1=-2 до x2=4 (для данного примера функции вводить не требуется, они уже введены автором), нажимаем Ok, получаем ответ.
Разберем более сложный случай, когда касательная должна проходить через точку не принадлежащую кривой.Пример 2. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 6).
Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3)=-9+12+2=5
1. a – абсцисса точки касания.2. f(a) = – a2 – 4a + 2.3. f '(x) = – 2x – 4, f '(a) = – 2a – 4.4. y = – a2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.6 = – a2 – 4a + 2 – 2(a + 2)(– 3 – a),a2 + 6a + 8 = 0 ^ a1 = – 4, a2 = – 2.Если a = – 4, то уравнение касательной имеет вид y = 4x + 18. Если a = – 2, то уравнение касательной имеет вид y = 6.
www.reshim.su
4.1.3 Уравнение касательной к графику функции
Видеоурок: Уравнение касательной к графику функции
Лекция: Уравнение касательной к графику функции
Если некоторая прямая проходит через точку с координатами (х0; f (х0)), а угол наклона данной прямой равен производной функции в данной токе, то такую прямую называют касательной к графику.
Обратите внимание, если не существует производной графика в данной точке, то и не может существовать касательной, или же данная касательная перпендикулярна к оси ОХ. Второй случай можно наблюдать в результате проведения касательной для графика функции арксинуса.
Итак, давайте рассмотрим задание касательной. Мы знаем, что для задания любой прямой, необходимо воспользоваться формулой y = kx + b.
Коэффициент k показывает, под каким углом будет располагаться прямая относительно оси ОХ. Если данный коэффициент больше нуля, то угол наклона между касательной и осью ОХ острый, если же коэффициент отрицательный, то угол между осью ОХ и касательной тупой.
Но давайте возвратимся к тому, что такое угловой коэффициент и как он находится. С прошлых вопросов мы помним, что угловой коэффициент – это производная функции в некоторой точке х0.
Чтобы задать уравнение касательной, необходимо воспользоваться формулой:
Итак, давайте рассмотрим подробнее, для этого необходимо провести аналогию между первоначальным уравнением прямой и уравнением касательной.
Отсюда следует, что для нахождения коэффициента k, необходимо найти производную в рассматриваемой точке.
Давайте найдем уравнение прямой для функции у = х3 в точке х0 = 3.
1. Находим производную данной функции:y' = 3x2.2. Как уже было сказано ранее, коэффициент – это производная функции в некоторой точке, поэтомуy'(3) = 3* 32 = 27.
3. Как видно из уравнения касательной, нам так же необходимо найти и значение функции в рассматриваемой точке f(x0):f(3) = 33 = 27.
Совершенно случайно получилось так, что значение производной в точке совпало со значением функции в заданной точке. Обратите внимание, что это просто совпадения и НЕ обязательно y' = f(x0).
4. Теперь давайте составим уравнение касательной по заданной формуле:у = 27 * (х – 3) + 27.
Чтобы получить конечно уравнение, необходимо сделать некоторые преобразования:у = 27 * (х – 3) + 27 = 27х – 81 + 27 = 27х - 54.
То есть уравнение касательной:у = 27х - 54.
Найти уравнение касательной достаточно просто, главное не запутаться в формуле. Для этого её необходимо просто выучить.
cknow.ru
Уравнение касательной и уравнение нормали к графику функции
Касательная - это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой.
Выведем уравнение касательной, а затем - уравнение нормали к графику функции.
Значение производной f '(x0) функции y = f(x) в точке x0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M0(x0, y0), где y0 = f(x0). В этом состоит геометрический смысл производной.
Таким образом, можем заменить k на f '(x0) и получить следующее уравнение касательной к графику функции:
y - y0 = f '(x0)(x - x0).
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль - это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:
(x - x0) + f '(x0)(y - y0) = 0
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет "холодным душем".
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример - тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг - приведение уравнения к общему виду.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Подставляем все полученные данные в "формулу-болванку" и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного "причесать": умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали - не заметить, что функция, данная в примере, - сложная и вычислять её производную как производную простой функции. Следующие примеры - уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Внимание! Данная функция - сложная, так как аргумент тангенса (2x) сам является функцией. Поэтому найдём производную функции как производную сложной функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Как и в предыдущем примере, данная функция - сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Поделиться с друзьями
Весь блок "Производная"
function-x.ru
Ответы@Mail.Ru: Касательная к графику функции.
А геометрический смысл производной не судьба выучить и решить устную задачу? Коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси OX) равен производной функции в точке xo . Если касательная параллельна g(x)=1-2x, то она имеет тот же угол наклона, т. е. угол между касательной и положительным направлением оси OX равен такому углу, у которого тангенс угла касательной равен -2 (g`(x)=(1-2x)`=-2). Значит, значение производной функции y=4x²-3x+5 в точке касания равно -2 Найдем абсциссу точки касания: f`(x)=(4x²-3x+5)`=-2, ->8x-3=-2, 8x=1, x=xo=1/8=0.125. Зная абсциссу токи касания, легко написать уравнение касательной: y=f(xo)+f`(xo)(x-xo), ->f(xo)=4*(1/8)²-3*(1/8)+5=75/16, f`(xo)=8*(1/8)-3=-2, y=f(xo)+f`(xo)(x-xo)=75/16-2(x-1/8)=79/16-2x=4.9375-2x Сравнивая g(x)=1-2x и y=79/16-2x=4.9375-2x нетрудно заметить, что g(x)=1-2x и y=79/16-2x=4.9375-2x параллельны, т. к. у обоих прямых одинаковый (равный) угол наклона (tg угла наклона =-2=g`(x)=(79/16-2x)`) Следовательно, задача решена верно и абсцисса точки касания xo=1/8=0.125, а ордината (для справки) точки касания yo=75/16=4 11/16=4.6875 <img src="//otvet.imgsmail.ru/download/65094_190e486c35acf219950529ad05cd991f_120x120.gif" data-hsrc="https://otvet.imgsmail.ru/download/65094_190e486c35acf219950529ad05cd991f_800.gif" ><img src="//otvet.imgsmail.ru/download/65094_1d431e34ae6bedb85b14ce9c1706a8f1_120x120.gif" data-hsrc="//otvet.imgsmail.ru/download/65094_1d431e34ae6bedb85b14ce9c1706a8f1_800.gif" >
Производная = 8х-3, она же в точке касания =-2. 8х-3=-2. 8х=1. х=1/8.
touch.otvet.mail.ru
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике - Элементы математического анализа
Секущая графика функции. Уравнение секущей графика функции
Рассмотрим график некоторой функции y = f (x), точки A= (x0; f (x0)) и B = (x1; f (x1)) на графике, прямую, проходящую через точки A и B, и произвольную точку C = (x; y) на этой прямой (рис. 1).
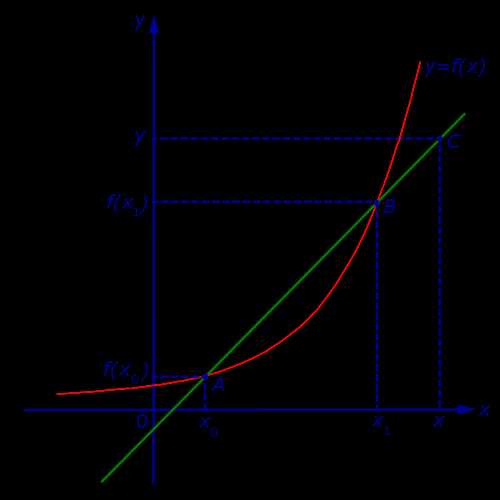
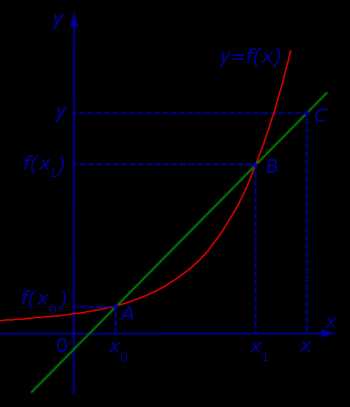
Рис.1
Определение 1. Прямую, проходящую через две произвольные точки графика функции, называют секущей графика функции.
В соответствии с определением 1 прямая, проходящая через точки A и B графика функции y = f (x), является секущей этого графика.
Выведем уравнение секущей графика функции.
Для этого рассмотрим векторы и , координаты которых имеют вид:
Поскольку векторы и лежат на одной прямой, то справедливо равенство
| (1) |
где k – некоторое число.
Переписывая равенство (1) в координатах, получим систему (2):
| (2) |
Исключая из системы (2) переменную k , получим систему (3):
| (3) |
второе уравнение которой можно записать в следующем виде
| (4) |
Уравнение (4) и является уравнением секущей графика функции y = f (x), проходящей через точки A = (x0; f (x0)) и B = (x1; f (x1)) этого графика.
Касательная к графику функции
Проведем секущую графика функции y = f (x), проходящую через точки A и B этого графика, и рассмотрим случай, когда точка A неподвижна, а точка B неограниченно приближается к точке A по графику функции y = f (x) (рис. 2).
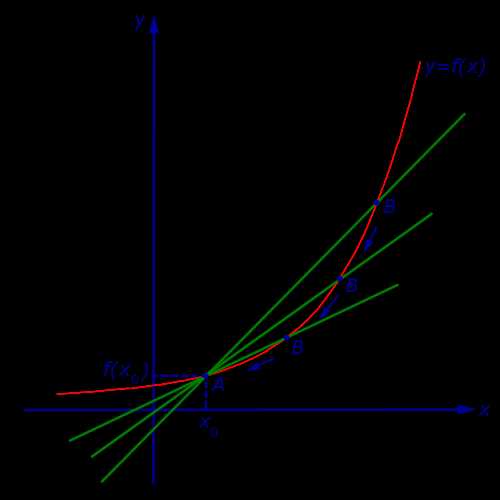
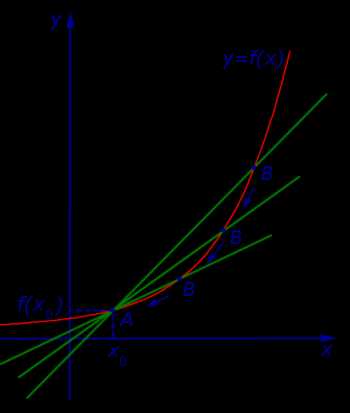
Рис.2
Неограниченное приближение точки B к точке A принято обозначать
B → A
и произносить «B стремится к A».
Заметим, что, если B → A для точек A = (x0; f (x0)) и B = (x1; f (x1)) графика функции y = f (x), то это означает, что x1 → x0 .
Определение 2. Если при x1 → x0 существует предельное положение секущей графика фукнкции y = f (x), то это предельное положение секущей называют касательной к графику функции y = f (x) в точке A = (x0; f (x0)) (рис. 3) .
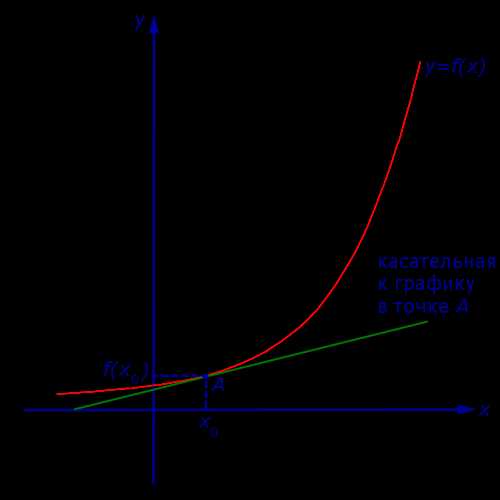
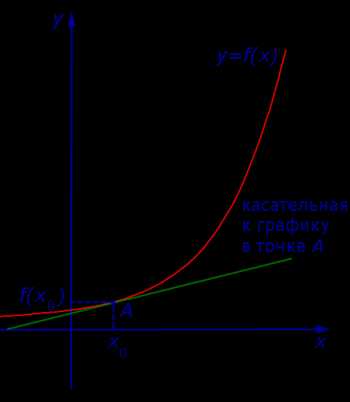
Рис.3
Производная функции
Определение 3. Если при x1 → x0 отношение
| (5) |
входящее в формулу (4), стремится к некоторому числу, то это число называют производной функции y = f (x) в точке x0 , обозначают f′(x0) или и записывают так:
| (6) |
Уравнение касательной к графику функции
Из формул (4) и (6) вытекает следующее
Утверждение. Если у функции y = f (x) существует производная в точке x0 , то к графику функции y = f (x) в точке с координатами (x0; f (x0)) можно провести касательную, а уравнение этой касательной имеет вид:
| y = f′(x0) (x – x0) + f (x0) | (7) |
Геометрический смысл производной
Рассмотрим сначала возрастающую функцию y = f (x) и проведем секущую графика этой функции, проходящую через точки A = (x0; f (x0)) и B = (x1; f (x1)) (рис. 4).
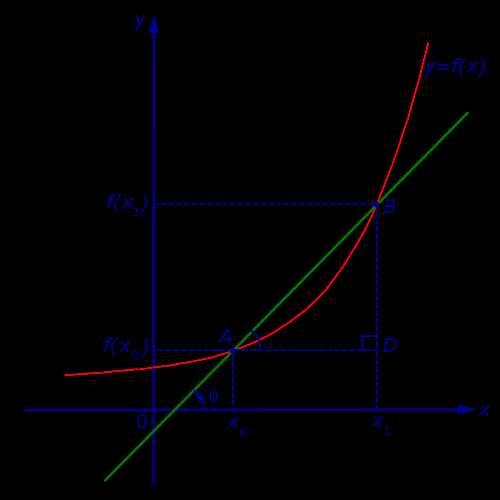
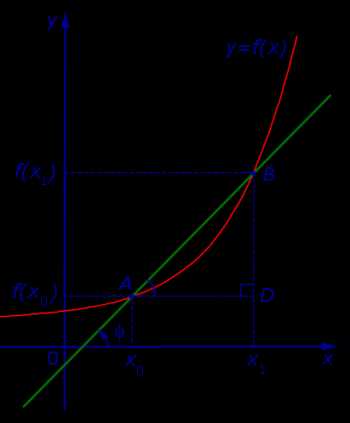
Рис.4
Обозначим буквой φ угол, образованный секущей и положительным направлением оси Ox, отсчитываемый против часовой стрелки. Тогда угол BAD в треугольнике ABD на рисунке 4 равен φ , и по определению тангенса угла получаем равенство
| (8) |
причем по определению углового коэффициента прямой tg φ является угловым коэффициентом секущей графика функции y = f (x), проходящей через точки A = (x0; f (x0)) и B = (x1; f (x1)) этого графика.
Случай, когда функция y = f (x) убывает, изображен на рисунке 5
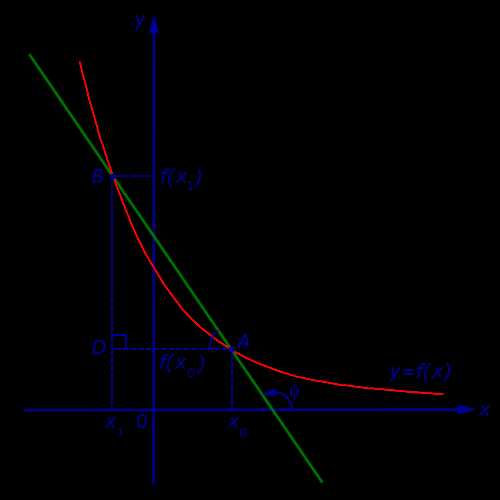
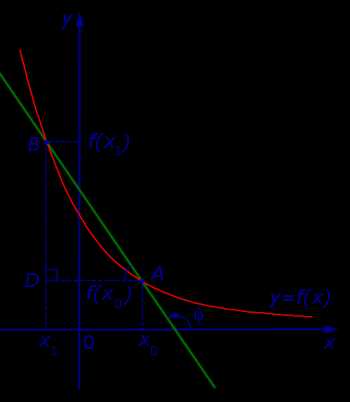
Рис.5
В этом случае угол φ является тупым, причем
то есть формула (8) справедлива и для случая, когда функция y = f (x) убывает.
Отсюда в соответствии с определением производной функции вытекает соотношение:
где буквой α обозначен угол, образованный касательной к графику функции y = f (x) в точке A = (x0; f (x0)) с положительным направлением оси Ox (рис. 6).
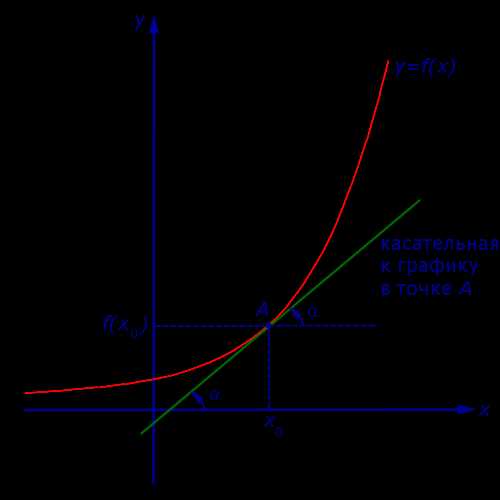
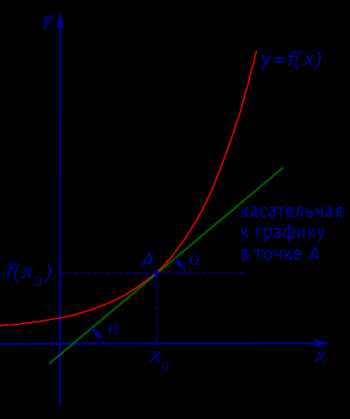
Рис.6
Таким образом, если у функции y = f (x) в точке x0 существует производная, то эта производная равна тангенсу угла наклона касательной к графику функции y = f (x) в точке (x0; f (x0)) :
f′(x0) = tg α ,
где угол наклона α образован касательной и положительным направлением оси Ox и отсчитывается в положительном направлении (то есть против часовой стрелки).
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru