ГлавнаяРазноеКак решать алгебра дроби

Как решать алгебраические дроби? Теория и практика. Как решать алгебра дроби


Как решать алгебраические дроби? Теория и практика

Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. Как решать алгебраические дроби? Вопрос, который будет мучить на протяжении всей школьной жизни.

Понятие алгебраической дроби

Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.

Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.

Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.

Основное правило обыкновенных дробей

Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей.

Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами.

Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.

Математические операции с дробями

Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.

Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но! Нужно помнить, что при наличии знака «–» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью.

Часто используется такое понятие, как сокращение дробей. Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру.

Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов:

  1. Нахождение НОД для обеих частей дроби.
  2. Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предшествующей.

Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть.

Несколько примеров с решениями

С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал.

1. Преобразовать дроби и привести их к общему знаменателю.

2. Преобразовать дроби и привести их к общему знаменателю.

3. Сократить указанные выражения (с использованием изученного основного правила дроби и сокращения степеней)

4. Сократить многочлены. Подсказка: нужно обнаружить формулы сокращенного умножения, привести к подобающему виду, сократить одинаковые элементы.

Задание на закрепление материала

1. Какие действия нужно произвести, что найти скрытое число? Решите примеры.

2. Умножьте и поделите дроби, пользуясь основным правилом.

После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно.

fb.ru

Как решать алгебраические дроби

Алгебраическая дробь — это выражение вида А/В, где буквы А и В обозначают любые числовые или буквенные выражения. Зачастую числитель и знаменатель в алгебраических дробях имеют громоздкий вид, но действия с такими дробями следует совершать по тем же правилам, что и действия с обыкновенными, где числитель и знаменатель — целые положительные числа.

Инструкция

completerepair.ru

Дроби

Дроби это тема, об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.

Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.

Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.

А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.

Что такое дробь?

Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.

Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.

Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.

Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:

Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:

А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:

Такие записи называют дробями. Дробь состоит из числителя и знаменателя.

Число, которое записывается сверху, называется числителем дроби.

Число, которое записывается снизу, называется знаменателем дроби.

В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.

Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?

Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):

Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».

Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?

Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:

Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».

Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:

Теперь представьте, что пиццу мы разделили на две части или, как говорят в народе: «Пополам»:

Допустим из этих двух кусков мы съели один кусок. Как записать такую дробь?

Очень просто. Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:

Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».

Дроби, которые мы сейчас рассмотрели, называют обыкновенными. Почему обыкновенными? Потому что дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Десятичные будем рассматривать немного позже. Обыкновенная дробь эта та дробь, которая состоит из числителя и знаменателя.

Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.

На следующем рисунке представлены три пиццы, которые разделены по разному. Если говорить о дробях, то у первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.

Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух) или, как говорят в народе: «половину» пиццы.

С помощью переменных дробь можно записать так:

где a — это числитель, b — знаменатель.

Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильные и неправильные.

Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:

Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.

С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:

Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это «чего-либо» разделено. А числитель показывает сколько этого «чего-либо» взяли.

Теперь возьмём к примеру неправильную дробь  и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.

Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:

Вообще, такие дроби даже не имеют права называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.

Допустим мы хотим съестьпиццы.  В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.

Дробь означает деление

Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.

Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».

Выделение целой части дроби

Вычислим дробь . Пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Проверка: (2 × 2) + 1 = 4 + 1 = 5

Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.

Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?

Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:

Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.

Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:

Схематически это выглядит так:

Процедуру, которую мы сейчас провели, называют выделением целой части дроби.

В нашем примере мы выделили целую часть дроби  и получили новую дробь .  Такую дробь называют смешанной. Смешанная дробь это дробь, у которой есть целая часть и дробная.

В нашем примере целая часть это 2, а дробная часть это

Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.

Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:

Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:

После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Главное понять, что куда отнести. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.

В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.

Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.

Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби 

Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:

Получили:

Перевод смешанного числа в неправильную дробь

Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается

Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель останется без изменения.

Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:

2 × 3 = 6

Затем к 6 прибавляем числитель дробной части:

6 + 1 = 7

Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменения:

Подробное решение выглядит так:

А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:

Пример 2. Перевести смешанное число в неправильную дробь.

Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменения:

Основное свойство дроби

Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Что это значит? Это значит, что значение дроби не изменится.

Например, рассмотрим дробь .  Умножим её числитель и знаменатель на одно и то же число, например на число 2:

Получили новую дробь .  Если верить основному свойству дроби, то дроби   и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.

Рассмотрим дробь  . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби и  равны между собой. Так ли это? Давайте проверим,  нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями  и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.

Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!

Сокращение дробей

Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .

Если при решении примеров получается большая некрасивая дробь, то нужно пытаться её сократить.

Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.

Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.

Пример 1.  Сократим дробь . Надо разделить числитель и знаменатель на наибольший общий делитель чисел 2 и 4.

В данном случае, дробь простая и для неё НОД ищется легко. НОД { 2 и 4 } это 2. Значит числитель и знаменатель дроби надо разделить на двойку. Итак, делим числитель и знаменатель на 2:

Пример 2. Сократим дробь . Чтобы сократить эту дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40. НОД { 20 и 40 } это 20. Значит делим числитель и знаменатель дроби на 20:

Пример 3. Сократим дробь . Чтобы сократить эту дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36. НОД { 32 и 36 } это 4. Значит делим числитель и знаменатель дроби на 4:

Если в числителе и знаменателе стоят простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:

Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.

Второй способ сокращения дроби

Второй способ является короткой версией первого способа. Суть данного способа заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.

К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4

Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение:

Суть в том, что число на которое разделили числитель и знаменатель хранят в уме. В нашем случае, числитель и знаменатель делят на 4 — это число и будем хранить в уме.

Сначала делим числитель на число 4. Полученный ответ записывают рядом с числителем, предварительно зачеркнув его:

Затем, точно так же делят знаменатель на число 4. Полученный ответ записывают рядом со знаменателем, предварительно зачеркнув его:

Затем собирают новую дробь. В числитель отправляют новое число 8 вместо 32, а в знаменатель отправляют новое число 9 вместо 36

Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.

Например, сократим дробь предварительно разложив на простые множители числитель и знаменатель:

Итак, мы разложили числитель и знаменатель дроби  на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.

Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:

Сократить можно ещё по тройке в числителе и в знаменателе:

Дальше сокращать больше нечего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, которого можно было бы сократить вместе с этой тройкой.

Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.

 Получили ответ . Значит при сокращении дроби получается новая дробь .

Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если вы только начинаете изучать математику. Практика показывает, что это оказывается сложным на первых этапах.

Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решен старым способом и будет выглядеть так:

Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:

Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?

Задания для самостоятельного решения

Задание 1. Запишите в виде дроби следующий рисунок:

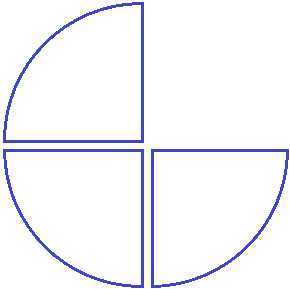
Задание 2. Запишите в виде дроби следующий рисунок:

Задание 3. Запишите в виде дроби следующий рисунок:

Задание 4. Запишите в виде дроби следующий рисунок:

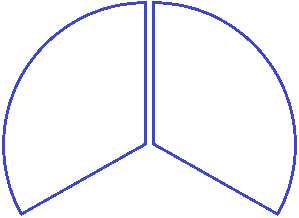
Задание 5. Запишите в виде дроби следующий рисунок:

Задание 6. Выделите целые части в следующих дробях:

Задание 7. Выделите целые части в следующих дробях:

Задание 8. Переведите смешанные дроби в неправильные:

Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части

Задание 10. Сократите следующую дробь на 3

Задание 11. Сократите следующую дробь на 3 вторым способом

Задание 12. Сократите следующую дробь на 5

Задание 13. Сократите следующую дробь на 5 вторым способом

Задание 14. Сократите следующие дроби:

Задание 15. Сократите следующие дроби вторым способом:

Задание 16. Запишите в виде дроби следующий рисунок:

Задание 17. Запишите в виде дроби следующий рисунок:

Задание 18. Запишите в виде дроби следующий рисунок:

Задание 19. Запишите в виде дроби следующий рисунок:

Задание 20. Запишите в виде дроби следующий рисунок:

Задание 21. Изобразите в виде рисунка следующую дробь:

Задание 22. Изобразите в виде рисунка следующую дробь:

Задание 23. Изобразите в виде рисунка следующую дробь:

Задание 24. Изобразите в виде рисунка следующую дробь:

Задание 25. Изобразите в виде рисунка следующую дробь:

Задание 26. Изобразите в виде рисунка следующую дробь:

Задание 27. Изобразите в виде рисунка следующую дробь:

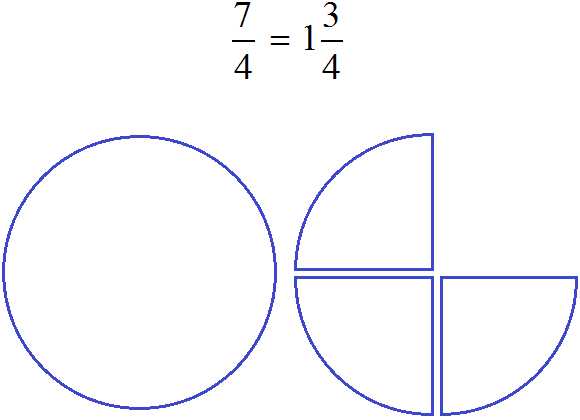
Задание 28. Изобразите в виде рисунка следующую дробь:

Задание 29. Изобразите в виде рисунка следующую дробь:

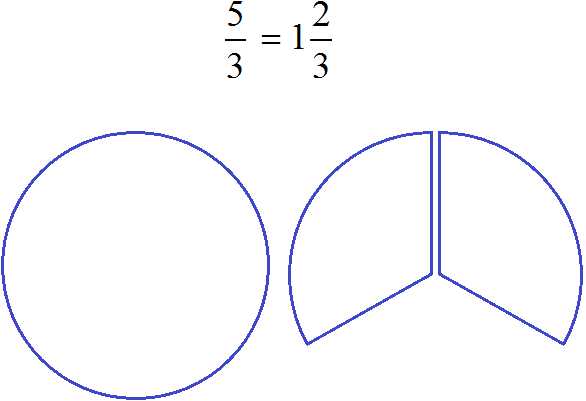
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

Что такое алгебраические дроби | Алгебра

Что такое алгебраические дроби?

Рассмотрим понятие алгебраической дроби.

Определение.

Алгебраическая дробь — это дробь, числитель и знаменатель которой — многочлены (причем знаменатель отличен от нуля).

Если ввести обозначение многочленов большими латинскими буквами: A, B, C, D, … ,  то алгебраическую дробь можно записать в виде

   

(где B≠0).

Другое название таких дробей — рациональные.

Определение.

Рациональная дробь — это дробь, числитель и знаменатель которой — многочлены (при условии, что знаменатель отличен от нуля).

Поскольку одночлен считают многочленом, состоящим из одного члена, в числителе и знаменателе алгебраических (рациональных) дробей могут стоять одночлены ( в том числе, числа).

Примеры алгебраических (рациональных) дробей:

   

   

   

   

   

   

Любой многочлен можно рассматривать как алгебраическую дробь, числитель которой равен этому многочлену, а знаменатель — единице.

Например,

   

   

   

Это и другие свойства алгебраических дробей мы рассмотрим подробнее в следующий раз.

www.algebraclass.ru

Как решать алгебраические дроби? Теория и практика

Образование 8 декабря 2017

Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. Как решать алгебраические дроби? Вопрос, который будет мучить на протяжении всей школьной жизни.

Понятие алгебраической дроби

Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.

Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.

Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.

Основное правило обыкновенных дробей

Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей.

Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами.

Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.

Видео по теме

Математические операции с дробями

Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.

Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но! Нужно помнить, что при наличии знака «–» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью.

Часто используется такое понятие, как сокращение дробей. Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру.

Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов:

  1. Нахождение НОД для обеих частей дроби.
  2. Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предшествующей.

Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть.

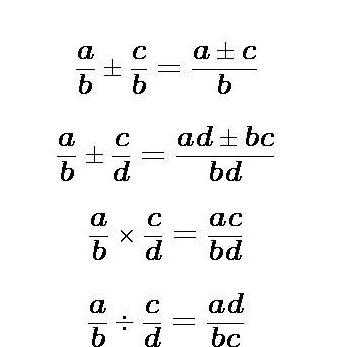
Несколько примеров с решениями

С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал.

1. Преобразовать дроби и привести их к общему знаменателю.

2. Преобразовать дроби и привести их к общему знаменателю.

3. Сократить указанные выражения (с использованием изученного основного правила дроби и сокращения степеней)

4. Сократить многочлены. Подсказка: нужно обнаружить формулы сокращенного умножения, привести к подобающему виду, сократить одинаковые элементы.

Задание на закрепление материала

1. Какие действия нужно произвести, что найти скрытое число? Решите примеры.

2. Умножьте и поделите дроби, пользуясь основным правилом.

После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно.

Источник: fb.ru Закон Как вступить в наследство: теория и практика

Смерть близкого человека – потеря, оправляться от которой придется долго. Между тем, как это ни банально, жизнь продолжается, она требует от нас в том числе ряда действий по оформлению документов, необходим...

Самосовершенствование Как правильно разговаривать? Теория и практика

Человеку свойственно пламенно желать общения с окружающими. Мы не можем без взаимодействия построить правильную самооценку и почувствовать себя действительно нужными. Поэтому люди, которым тяжело дается общение, чувст...

Автомобили Парковка задним ходом - теория и практика

Парковка задним ходом для начинающих автомобилистов и автоледи - настоящий камень преткновения. Новички обычно не очень хорошо чувствуют габариты автомобиля, а в условиях плотного окружения другими машинами неосторожн...

Бизнес Травление металлов: теория и практика

Химическое травление металла означает удаление с его поверхности остатков флюсов или окислов. Такой процесс предполагает использование раствора хлористых солей, щелочи или раствора кислоты. Вне зависимости от того, ка...

Дом и семья Сколько должен съесть новорожденный: теория и практика

Сколько должен съесть новорожденный за один раз и за сутки, наедается ли ребенок, достаточно ли вырабатывается молока – это вопросы, которые больше всего интересуют женщин в первые дни, когда мама и ребенок толь...

Дом и семья Когда начинает разговаривать ребенок: теория и практика

Мамы нередко очень обеспокоены ситуацией, когда соседский малыш, ровесник собственного ребенка, уже вовсю произносит первые слова, а от своего чада не слышно ни звука. Ситуацию накаляют и врачи, отчего-то очень полюби...

Духовное развитие Что такое карма? Диагностика кармы: теория и практика

Жизнь полна неожиданностей. Не бывает двух одинаковых судеб: одни счастливы, другим приходится бороться с неприятностями, преодолевать препятствия. Почему так происходит? Тот, кто интересовался этим, неизбежно сталкив...

Закон Теория и практика наказания за оскорбление личности

Современное российское законодательство трактует оскорбление личности как унижение достоинства и чести в неприличной форме.

Компьютеры Разгон процессора Intel. Теория и практика

В настоящее время основными производителями центральных процессоров для персональных компьютеров являются две крупные компании – Intel и AMD. Альтернативные решения если и есть, то либо их слишком мало, чтобы ка...

Новости и общество Национал-социализм: теория и практика «расовой гигиены»

В истории, пожалуй, не было более бесчеловечной идеологии, чем национал-социализм. Возведенная нацистами Третьего Рейха в ранг официальной политики государства и национальной идеологии Германии, теория «расовой ...

monateka.com

Алгебраические дроби. Методическая разработка

Дополнительные сочинения

Этот урок является одним из итоговых по знаниям алгебры 8-ого класса. Мы с вами вспомним основные определения и примеры решения задач на тему «Алгебраические дроби».

Тема: Повторение курса алгебры 8-ого класса

Урок: Алгебраические дроби

1. Определение алгебраической дроби

Для начала давайте вспомним, что же такое алгебраические дроби. Алгебраической дробью называют выражение вида , где – многочлены, – числитель, – знаменатель.

Поскольку – многочлены, то необходимо иметь в виду стандартные действия, возможные с многочленами, а именно: приведение к стандартному виду, разложение на множители, а также сокращение числителя и знаменателя.

2. Решение примеров

Пример №1

Сократите дробь

– воспользуемся формулами сокращённого умножения для квадрата суммы и разности квадратов.

Комментарии: вначале мы разложили дробь на множители с помощью формул сокращённого умножения, а дальше воспользовались одним из основных свойств дроби: и числитель, и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен, в том числе число, который не равен 0. Таким образом получается, что мы и числитель, и знаменатель разделили на многочлен , поэтому обязательно необходимо учесть, что этот многочлен не равен 0, т. е. .

Пример №2

Из условия нам пока не ясно, какая связь между этими двумя функциями. Для этого нам необходимо упростить первую из них методом разложения на множители.

однако необходимо не забыть про условие сокращения дроби, т. е. про то, что

После всех сокращений мы получаем, что

лишь с тем отличием, что .

Построим график двух функций.

Мы видим яркое различие этих двух графиков: по сути они одинаковы, но на первом графике нам необходимо выколоть точку с координатой (1;0), поскольку эта точна не входит в ОДЗ первой функции.

Итого, мы с вами рассмотрели, что такое дробь, решили пару примеров о том, как важно следить за областью определения (областью допустимых значений), т. е. за теми значениями, которые может принимать .

3. Действия, которые можно производить с алгебраическими дробями

Теперь перейдём к вопросу, какие действия можно производить с алгебраическими дроями, помимо тех, которые уже были упомянуты выше.

Естественно, алгебраические дроби, как и арифметические дроби, можно складывать, вычитать, умножать, делить, возводить в степень, получая при этом рациональные алгебраические выражения (такие выражения, которые составлены из чисел, переменных с помощью арифметических операций и возведения в натуральную степень). После определённых упрощений подобные выражения сводятся к дробям, для которых исходными выражениями также являются алгебраические дроби.

Список действий / условий, с которыми можно столкнуться, решая задачи на алгебраические дроби:

- Упростить рациональные выражения

- Доказать тождества

- Решать рациональное уравнение

- Упростить/вычислить дробь

4. Решение задач

Пример №3

Решить простейшее рациональное уравнение

       

Дробь равна 0 тогда и только тогда, когда числитель равен 0, а знаменатель не равен 0. В нашем случае знаменатель равен . Значит, решение дроби сводится к линейному уравнению

Ответ:

Пример №4

Решить уравнение

В первую очередь попытаемся сократить дробь

, при условии, что .

Поскольку мы уже упростили дробь в левой части исходного уравнения, то можем подставить новое значение и решить уравнение.

Теперь давайте попробуем выделить полный квадрат из полученного квадратного уравнения

Воспользуемся формулой сокращённого умножения для разности квадратов

Произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. К тому же не забываем, что в начале у нас появилось условие существования нашего выражения в виде . Запишем же систему уравнений.

=> => Мы видим, что противоречит нашему условию, что , поэтому у нас остаётся только один ответ .

Ответ: .

Итак, посмотрим на особенности, которые имеет решённый нами выше пример:

1. Числитель с разностью кубов и знаменатель желательно сократить сразу, поскольку это возможно в данном случае и сильно упростит дальнейшее решение уравнения, однако обязательно нужно помнить о том, что знаменатель дроби не может равняться, 0 и записать это условие.

2. Приведя дробь к квадратному уравнению, мы вспомнили один из методов решения квадратных уравнений – метод выделения полного квадрата.

5. Вывод

Мы с вами на данном уроке вспомнили, что такое алгебраическая дробь, какие действия необходимо производить с числителем и знаменателем при решении таких дробей, какие действия в общем можно производить с дробями такого вида и решили несколько простых задач.

Список литературы

Башмаков М. И. Алгебра 8 класс. – М.: Просвещение, 2004. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010. Никольский С. М., Потапов М. А., Решетников Н. Н., Шевкин А. В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Вся элементарная математика . Школьный помощник . Интернет-портал Testmath. com.

dp-adilet.kz

8 класс. Алгебра. Алгебраические дроби. - Сложение и вычитание алгебраических дробей.

Комментарии преподавателя

В данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему – сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров

 

Сфор­му­ли­ру­ем пра­ви­ло сло­же­ния (вы­чи­та­ния) ал­геб­ра­и­че­ских дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми (оно сов­па­да­ет с ана­ло­гич­ным пра­ви­лом для обык­но­вен­ных дро­бей):  То есть для сло­же­ния или вы­чи­та­ния ал­геб­ра­и­че­ских дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми необ­хо­ди­мо со­ста­вить со­от­вет­ству­ю­щую ал­геб­ра­и­че­скую сумму чис­ли­те­лей, а зна­ме­на­тель оста­вить без из­ме­не­ний.

Это пра­ви­ло мы раз­бе­рём и на при­ме­ре обык­но­вен­ных дро­бей, и на при­ме­ре ал­геб­ра­и­че­ских дро­бей.

При­мер 1. Сло­жить дроби: .

Ре­ше­ние

Сло­жим чис­ли­те­ли дро­бей, а зна­ме­на­тель оста­вим таким же. После этого раз­ло­жим чис­ли­тель и зна­ме­на­тель на про­стые мно­жи­те­ли и со­кра­тим. По­лу­чим: .

При­ме­ча­ние: стан­дарт­ная ошиб­ка, ко­то­рую до­пус­ка­ют при ре­ше­нии по­доб­но­го рода при­ме­ров, за­клю­ча­ет­ся в сле­ду­ю­щем спо­со­бе ре­ше­ния: . Это гру­бей­шая ошиб­ка, по­сколь­ку зна­ме­на­тель оста­ёт­ся таким же, каким был в ис­ход­ных дро­бях.

Ответ: .

При­мер 2. Сло­жить дроби: .

Ре­ше­ние

Дан­ная за­да­ча ничем не от­ли­ча­ет­ся от преды­ду­щей: .

Ответ: .

От обык­но­вен­ных дро­бей пе­рей­дём к ал­геб­ра­и­че­ским.

При­мер 3. Сло­жить дроби: .

Ре­ше­ние:как уже го­во­ри­лось выше, сло­же­ние ал­геб­ра­и­че­ских дро­бей ничем не от­ли­ча­ет­ся от сло­же­ния обык­но­вен­ных дро­бей. По­это­му метод ре­ше­ния такой же: .

Ответ: .

При­мер 4. Вы­честь дроби: .

Ре­ше­ние

Вы­чи­та­ние ал­геб­ра­и­че­ских дро­бей от­ли­ча­ет­ся от сло­же­ния толь­ко тем, что в чис­ли­тель за­пи­сы­ва­ет­ся раз­ность чис­ли­те­лей ис­ход­ных дро­бей. По­это­му .

Ответ: .

При­мер 5. Вы­честь дроби: .

Ре­ше­ние: .

Ответ: .

При­мер 6. Упро­стить: .

Ре­ше­ние: .

Ответ: .

В дроби, ко­то­рая по­лу­ча­ет­ся в ре­зуль­та­те сло­же­ния или вы­чи­та­ния, воз­мож­ны со­кра­ще­ния. Кроме того, не стоит за­бы­вать об ОДЗ ал­геб­ра­и­че­ских дро­бей.

При­мер 7. Упро­стить: .

Ре­ше­ние: .

При этом . Во­об­ще, если ОДЗ ис­ход­ных дро­бей сов­па­да­ет с ОДЗ ито­го­вой, то его можно не ука­зы­вать (ведь дробь, по­лу­чен­ная в от­ве­те, также не будет су­ще­ство­вать при со­от­вет­ству­ю­щих зна­че­ни­ях пе­ре­мен­ных). А вот если ОДЗ ис­ход­ных дро­бей и от­ве­та не сов­па­да­ет, то ОДЗ ука­зы­вать необ­хо­ди­мо.

Ответ: .

При­мер 8. Упро­стить: .

Ре­ше­ние: . При этом y (ОДЗ ис­ход­ных дро­бей не сов­па­да­ет с ОДЗ ре­зуль­та­та).

Ответ: .

 

Чтобы скла­ды­вать и вы­чи­тать ал­геб­ра­и­че­ские дроби с раз­ны­ми зна­ме­на­те­ля­ми, про­ве­дём ана­ло­гию с обык­но­вен­ны­ми дро­бя­ми и пе­ре­не­сём её на ал­геб­ра­и­че­ские дроби.

 Рас­смот­рим про­стей­ший при­мер для обык­но­вен­ных дро­бей.

При­мер 1. Сло­жить дроби: .

Ре­ше­ние:

Вспом­ним пра­ви­ло сло­же­ния дро­бей. Для на­ча­ла дроби необ­хо­ди­мо при­ве­сти к об­ще­му зна­ме­на­те­лю. В роли об­ще­го зна­ме­на­те­ля для обык­но­вен­ных дро­бей вы­сту­па­ет наи­мень­шее общее крат­ное (НОК) ис­ход­ных зна­ме­на­те­лей.

Опре­де­ле­ние

 – наи­мень­шее на­ту­раль­ное число, ко­то­рое де­лит­ся од­но­вре­мен­но на числа  и .

Для на­хож­де­ния НОК необ­хо­ди­мо раз­ло­жить зна­ме­на­те­ли на про­стые мно­жи­те­ли, а затем вы­брать все про­стые мно­жи­те­ли, ко­то­рые вхо­дят в раз­ло­же­ние обоих зна­ме­на­те­лей.

; . Тогда в НОК чисел  долж­ны вхо­дить две двой­ки и две трой­ки: .

После на­хож­де­ния об­ще­го зна­ме­на­те­ля, необ­хо­ди­мо для каж­дой из дро­бей найти до­пол­ни­тель­ный мно­жи­тель (фак­ти­че­ски, по­де­лить общий зна­ме­на­тель на зна­ме­на­тель со­от­вет­ству­ю­щей дроби).

.

Затем каж­дая дробь умно­жа­ет­ся на по­лу­чен­ный до­пол­ни­тель­ный мно­жи­тель. По­лу­ча­ют­ся дроби с оди­на­ко­вы­ми зна­ме­на­те­ля­ми, скла­ды­вать и вы­чи­тать ко­то­рые мы на­учи­лись на про­шлых уро­ках.

По­лу­ча­ем: .

Ответ:.

Рас­смот­рим те­перь сло­же­ние ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми. Сна­ча­ла рас­смот­рим дроби, зна­ме­на­те­ли ко­то­рых яв­ля­ют­ся чис­ла­ми.

При­мер 2. Сло­жить дроби: .

Ре­ше­ние:

Ал­го­ритм ре­ше­ния аб­со­лют­но ана­ло­ги­чен преды­ду­ще­му при­ме­ру. Легко по­до­брать общий зна­ме­на­тель дан­ных дро­бей:  и до­пол­ни­тель­ные мно­жи­те­ли для каж­дой из них.

.

Ответ:.

Итак, сфор­му­ли­ру­ем ал­го­ритм сло­же­ния и вы­чи­та­ния ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми:

1. Найти наи­мень­ший общий зна­ме­на­тель дро­бей.

2. Найти до­пол­ни­тель­ные мно­жи­те­ли для каж­дой из дро­бей (по­де­лив общий зна­ме­на­тель на зна­ме­на­тель дан­ной дроби).

3. До­мно­жить чис­ли­те­ли на со­от­вет­ству­ю­щие до­пол­ни­тель­ные мно­жи­те­ли.

4. Сло­жить или вы­честь дроби, поль­зу­ясь пра­ви­ла­ми сло­же­ния и вы­чи­та­ния дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми.

Рас­смот­рим те­перь при­мер с дро­бя­ми, в зна­ме­на­те­ле ко­то­рых при­сут­ству­ют бук­вен­ные вы­ра­же­ния.

При­мер 3. Сло­жить дроби: .

Ре­ше­ние:

По­сколь­ку бук­вен­ные вы­ра­же­ния в обоих зна­ме­на­те­лях оди­на­ко­вы, то сле­ду­ет найти общий зна­ме­на­тель для чисел . Ито­го­вый общий зна­ме­на­тель будет иметь вид: . Таким об­ра­зом, ре­ше­ние дан­но­го при­ме­ра имеет вид:.

Ответ:.

При­мер 4. Вы­честь дроби: .

Ре­ше­ние:

Если «схит­рить» при под­бо­ре об­ще­го зна­ме­на­те­ля не уда­ёт­ся (нель­зя раз­ло­жить на мно­жи­те­ли или вос­поль­зо­вать­ся фор­му­ла­ми со­кра­щён­но­го умно­же­ния), то в ка­че­стве об­ще­го зна­ме­на­те­ля при­хо­дит­ся брать про­из­ве­де­ние зна­ме­на­те­лей обеих дро­бей.

.

Ответ:.

Во­об­ще, при ре­ше­нии по­доб­ных при­ме­ров, наи­бо­лее слож­ным за­да­ни­ем яв­ля­ет­ся на­хож­де­ние об­ще­го зна­ме­на­те­ля.

Рас­смот­рим более слож­ный при­мер.

При­мер 5. Упро­стить: .

Ре­ше­ние:

При на­хож­де­нии об­ще­го зна­ме­на­те­ля необ­хо­ди­мо пре­жде всего по­пы­тать­ся раз­ло­жить зна­ме&s

www.kursoteka.ru