ГлавнаяРазноеКак составить уравнение плоскости по 3 точкам

Уравнения плоскости: общее, через три точки, нормальное. Как составить уравнение плоскости по 3 точкам


Уравнение плоскости по трем точкам

Во многих стереометрических задачах, связанных с нахождением расстояния от точки до плоскости или расстояния между скрещивающимися прямыми, или угла между плоскостями, требуется найти уравнение плоскости. В этой статье я расскажу, как найти уравнение плоскости, если известны координаты трех точек, через которые она проходит.

Уравнение плоскости имеет вид: , где , , и  - числовые коэффициенты.

Пусть  нам нужно написать уравнение плоскости, которая проходит через точки , и  

Так как точки принадлежат плоскости, то при подстановке их координат в уравнение плоскости, мы получим верные равенства.

Так как у нас три точки, мы должны получить систему из трех уравнений с четырьмя неизвестными. Примем коэффициент  равным 1. Для этого разделим уравнение плоскости на  .  Получим:

Мы можем переписать  это уравнение в виде: 

Внимание! Если плоскость проходит через начало координат, то принимаем d=0.

Чтобы найти коэффициенты А, В и С, подставим координаты точек , и   в уравнение плоскости .

Получим систему уравнений:

Решив ее, мы найдем значения коэффициентов А, В и С.

Решим задачу.

В правильной четырехугольной призме  со стороной основания 12 и высотой 21 на ребре  взята точка  так, что  равно 8. на ребре  взята точка  так, что  равно 8. Написать уравнение плоскости :

Поскольку для нахождения уравнения плоскости нам понадобятся координаты точек, я сразу помещаю призму в систему координат:

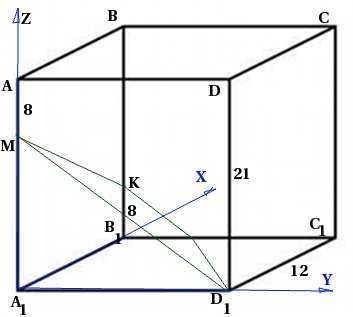
Запишем координаты точек:

Подставим их в систему уравнений:

Отсюда:

Подставим найденные коэффициенты в уравнение плоскости:

Чтобы избавиться от дробных коэффициентов, умножим обе части уравнения плоскости на . Получим:

Ответ: уравнение плоскости   

 

И.В. Фельдман, репетитор по математике.

 

ege-ok.ru

общее, через три точки, нормальное

Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.

Итак, пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей ненулевой вектор называется вектором нормали к этой плоскости.

Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:

Чтобы получить уравнение плоскости, заданной этими условиями, и имеющее приведённый вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1), а для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е.

.

Вектор задан по условию. Координаты вектора найдём по формуле :

.

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

. (1)

Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение. Используя формулу (1), имеем:

,

откуда после преобразований получим

.

Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.

Итак, уравнение вида

    (2)

называется общим уравнением плоскости.

Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат. Поэтому, если примем в заданном уравнении x = y = 0, получим z = 6. Следовательно, заданная плоскость пересекает ось Oz в точке A(0; 0; 6). Аналогично, при x = z = 0 получим y = -3, т.е. точку B(0; -3; 0). А при y = z = 0 получим x = 2, т.е. точку C(2; 0; 0). По трём точкам A(0; 0; 6), B(0; -3; 0) и C(2; 0; 0) строим заданную плоскость.

Решения типичных задач, которые бывают на контрольных работах - в пособии "Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке".

Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.

1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению.

2. При A = 0 уравнение определяет плоскость, параллельную оси Ox, поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость параллельная оси Oy, а при C = 0 плоскость параллельна оси Oz.

3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость проходит через ось Oy, а плоскость через ось Oz.

4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz, а плоскость - плоскости xOz.

5. При A = B = D = 0 уравнение (или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz, а уравнение x = 0 - координатную плоскость yOz.

Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение

Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .

Посмотреть правильное решение и ответ.

Решения типичных задач, которые бывают на контрольных работах - в пособии "Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке".

Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.

Используя выражение смешанного произведения в координатах, получим уравнение плоскости

    (3)

После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.

Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:

, ,

и определить частный случай общего уравнения прямой, если такой имеет место.

Решение. По формуле (3) имеем:

Раскрываем определитель по первой строке:

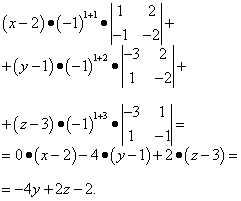
Получили общее уравнение плоскости

или после деления на -2:

.

Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.

Решения типичных задач, которые бывают на контрольных работах - в пособии "Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке".

Нормальным уравнением плоскости называется её уравнение, записанное в виде

,

где - направляющие косинусы нормали плоскости, - расстояние от начала координат до плоскости.

Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости. (Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости - в трёх).

Пусть M - какая угодно точка пространства. Для нахождения отклонения точки M от плоскости следует в левую часть нормального уравнения плоскости подставить на место x, y и z подставить координаты этой точки.

Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.

,

так как расстояние не может быть отрицательным числом.

Общее уравнение плоскости

приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой

.

Знак нормирующего множителя берётся противоположным знаку свободного члена в общем уравнении плоскости.

Пример 6. Привести уравнение плоскости к нормальному виду.

Решение. Вычислим нормирующий множитель:

.

Знак нормирующего множителя положительный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим требуемое в условии примера нормальное уравнение плоскости:

.

Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3), а плоскость задана общим уравнением .

Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:

.

Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:

.

Вычислим отклонение точки от плоскости:

Найдём теперь расстояние от точки до плоскости как модуль отклонения:

Всё по теме "Прямая и плоскость"

function-x.ru

§6. Другие виды уравнения плоскости

I Уравнение плоскости, проходящей через три точки

Выведем уравнение плоскости, которая проходит через три различные точки M1(x1,y1,z1), M2(x2,y2,z2) и M3(x3,y3,z3), не лежащие на одной прямой. Так как указанные точки не лежат на одной прямой, векторы инеколлинеарны, а потому произвольная точкаM(x,y,z) лежит в одной плоскости с точками M1, M2, M3 тогда и только тогда, когда векторы ,икомпланарны. Но компланарность равносильна равенству нулю смешанного произведения векторов. Записав смешанное произведение через проекции векторов, получим:

. (1)

Это и есть уравнение плоскости проходящей через данные три точки.

II Уравнение плоскости “в отрезках”

Рассмотрим плоскость, которая пересекает все координатные оси и не проходит через начало координат. Введем обозначения для точек пересечения с осями: M1(a;0;0), M2(0;b;0) и M3(0;0;c). Составим уравнение плоскости, используя формулу (1):

.

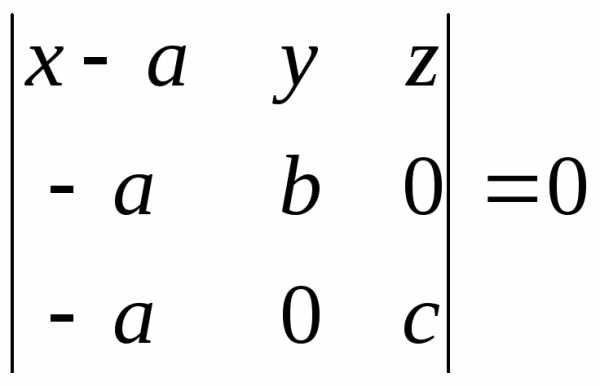Вычислив определитель, получим:

(x–a)bc+yac+zab=0.

Разделим обе части уравнения на abc:

.

И окончательно

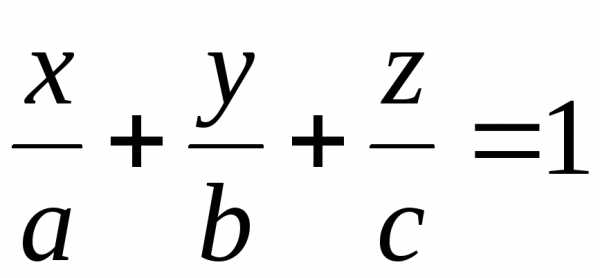. (2)

Это и есть уравнение плоскости “в отрезках”.

§7. Прямая в пространстве

I Общие уравнения прямой

Как уже говорилось ранее, в аналитической геометрии линию в пространстве понимают как пересечение двух поверхностей. В частности, прямую линию мы будем рассматривать как пересечение двух плоскостей. Поэтому, если в пространстве задананекоторая ДПСК,то уравнениями прямойслужит система двух уравнений первой степени:

(1)

Будем называть эти уравнения общими уравнениями прямой (конечно, предполагается, что прямые пересекаются).

Очевидно, существует бесчисленное множество пар плоскостей, пересекающихся по данной прямой, и соответственно этому существует бесчисленное множество общих уравнений (1) для данной прямой.

Общие уравнения удобны при решении задачи о пересечении прямой и плоскости или двух прямых, задачи о проектировании прямой на плоскость. В других задачах более удобными оказываются иные формы уравнений прямой.

II Канонические уравнения прямой

Определение. Всякий ненулевой вектор, лежащий на данной прямой или параллельный ей, называется ее направляющим вектором. Обозначение: .

Составим уравнение прямой, проходящей через точку M0(x0,y0,z0) в направлении вектора . Возьмем текущую точку прямойM(x,y,z) и рассмотрим вектор . Он лежит на данной прямой и поэтому коллинеарен ее направляющему вектору. Осталось написать условие коллинеарности, т.е. пропорциональность проекций:

. (2)

Это и есть канонические уравнения прямой, проходящей через точку M0(x0,y0,z0) и имеющей направляющий вектор .

Пример. Найти канонические уравнения прямой

(3)

Решение. Чтобы составить канонические уравнения прямой, нужно: 1) найти какую-либо точку прямой; 2) найти направляющий вектор прямой.

1) Найти какую-нибудь точку прямой (3) – это означает найти какое-нибудь решение этой системы двух уравнений с тремя неизвестными. Положим, например, x=0. Система (3) превратится в

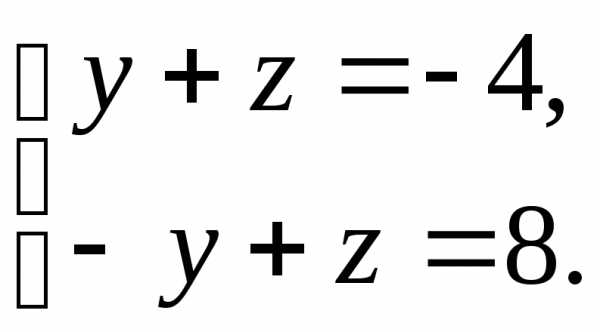
Отсюда нетрудно найти: z=2, y= –6. Итак, точка M0(0;–6; 2) принадлежит прямой (3).

2) Прямая определена как пересечения двух плоскостей, значит она лежит в каждой из них и поэтому перпендикулярна их нормальным векторам и. В качестве направляющего вектора можно взять любой вектор перпендикулярный к векторами, например, их векторное произведение

,

или вектор, коллинеарный ему . Итак, искомые канонические уравнения имеют вид

Пример. Составить уравнения прямой, проходящей через точки M1(x1,y1,z1) и M2(x2,y2,z2).

Решение. Для того, чтобы использовать канонические уравнения (2), положим M0=M1, . Получим:

. (4)

Имея эти уравнения, предыдущей пример можно решить, не находя направляющий вектор прямой. Надо только найти не одну точку, лежащую на прямой, а две.

studfiles.net

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

⇐ Предыдущая12

Если заданы координаты трех точек A(x1, y1, z1) B(x2, y2, z2) и C(x3, y3, z3),

лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле

x - x 1 y - y 1 z - z 1 = 0
x 2 - x 1 y 2 - y 1 z 2 - z 1
x 3 - x 1 y 3 - y 1 z 3 - z 1

 

 

13.Угол между плоскостями, расстояние от точки до плоскости.

 

Пусть плоскости α и β пересекаются по прямой с. Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.

Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны,

Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:

Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.

 

расстояние от точки до плоскости

Теорема

Рассмотрим точку T, заданную своими координатами:

T = (x0, y0, z0)

Также рассмотрим плоскость α, заданную уравнением:

Ax + By + Cz + D = 0

Тогда расстояние L от точки T до плоскости α можно считать по формуле:

Другими словами, мы подставляем координаты точки в уравнение плоскости, а затем делим это уравнение на длину вектора-нормали n к плоскости:

n = (A, B, C)

Полученное число и есть расстояние. Давайте посмотрим, как эта теорема работает на практике.

 

 

14.Прямая в пространстве, ее параметрическое уравнение.

 

Мы уже выводили параметические уравнения прямой на плоскости, давайте получим параметрические уравнения прямой, которая задана в прямоугольной системе координат в трехмерном пространстве.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую a (смотрите раздел способы задания прямой в пространстве), указав направляющий вектор прямой и координаты некоторой точки прямой . От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве.

Пусть - произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М1, то мы получим координаты вектора (смотрите статью нахождение координат вектора по координатам точек его конца и начала), то есть, .

Очевидно, что множество точек определяет прямую а тогда и только тогда, когда векторы и коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов и : , где - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра .

Приведем пример параметрических уравнений прямой в прямоугольной системе координат Oxyz в пространстве: . Здесь

 

15.Угол между прямой и плоскостью. Точка пересечения прямой с плоскостью.

 

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0 (3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (3.2)

2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями:

=; (3.3)

3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a(m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

. (3.4)

Уравнения (3.4) называются каноническими уравнениями прямой.

Векторa называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:

x = x1 +mt, y = y1 + nt, z = z1 + рt. (3.5)

Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:

x = mz + a, y = nz + b. (3.6)

От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n= [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Система равносильна системе x = x1, y = y1; прямая параллельна оси Oz.

Пример 1.15. Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

Решение. По условию задачи вектор ОА(1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде x-y+3z+D=0. Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3×3+D = 0 Þ D = -11. Итак, x-y+3z-11=0.

Пример 1.16. Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 2x+y-z-7=0 угол 60о.

Решение. Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В неравно 0, A/Bx+y=0. По формуле косинуса угла между двумя плоскостями

.

Решая квадратное уравнение 3m2 + 8m - 3 = 0, находим его корниm1 = 1/3, m2 = -3, откуда получаем две плоскости 1/3x+y = 0 и -3x+y = 0.

Пример 1.17. Составьте канонические уравнения прямой:5x + y + z = 0, 2x + 3y - 2z + 5 = 0.

Решение. Канонические уравнения прямой имеют вид:

где m, n, р - координаты направляющего вектора прямой, x1, y1, z1 - координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, x=0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть x=0, тогда y + z = 0, 3y - 2z+ 5 = 0, откуда y=-1, z=1. Координаты точки М(x1, y1, z1 ), принадлежащей данной прямой, мы нашли: M (0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей n1(5,1,1) иn2(2,3,-2). Тогда

Канонические уравнения прямой имеют вид: x/(-5) = (y + 1)/12 == (z - 1)/13.

Пример 1.18. В пучке, определяемом плоскостями 2х-у+5z-3=0 и х+у+2z+1=0, найти две перпендикулярные плоскости, одна из которых проходит через точку М(1,0,1).

Решение. Уравнение пучка, определяемого данными плоскостями, имеет вид u(2х-у+5z-3) + v(х+у+2z+1)=0, где u и v не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:

(2u +v)x + (- u + v)y + (5u +2v)z - 3u + v = 0.

Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:

(2u+v)×1 + ( -u + v)×0 + (5u + 2v )×1 -3u + v =0, или v = - u.

Тогда уравнение плоскости, содержащей M, найдем, подставив v = - u в уравнение пучка:

u(2x-y +5z - 3) - u (x + y +2z +1) = 0.

Т.к. u¹0 ( иначе v=0, а это противоречит определению пучка ), то имеем уравнение плоскости x-2y+3z-4=0. Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:

(2u+ v)×1 + (v - u)×(-2) + (5u +2v)×3 = 0, или v = - 19/5u.

Значит, уравнение второй плоскости имеет вид:

u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 или 9x +24y + 13z + 34 = 0

 

⇐ Предыдущая12 

infopedia.su

Уравнение плоскости, проходящей через три точки

Даны три точки

,

не лежащие на одной прямой. Требуется написать уравнение плоскости, проходящей через эти три точки. Из геометрии известно, что такая плоскость существует и единственная. Так как она проходит через точку , то ее уравнение имеет вид

,      (9)

где , ,  одновременно не равны нулю. Так как она проходит еще через точки , , то должны выполняться условия:

                                          (10)

Составим однородную линейную систему уравнений относительно  неизвестных , , :

                                           (11)

Здесь  есть произвольная точка, удовлетворяющая уравнению плоскости (9). В силу (9) и (10) системе (11) удовлетворяет нетривиальный вектор , поэтому определитель этой системы равен нулю

.

Мы получили уравнение вида (9), т. е. уравнение плоскости, в чем легко убедиться, разложив полученный определитель по элементам первой строки. При этом эта плоскость проходит через точки , , , что вытекает из свойств определителя. Наша задача решена.

Уравнение (12) можно еще написать и в следующем виде:

.                         (13)

Если из первой, третьей и четвертой строк определителя в (13) вычесть вторую строку, то он не изменится. Разлагая результат по элементам четвертого столбца, получим уравнение (12).

Уравнение плоскости, проходящей через две точки и параллельной данному вектору. Если задан векторИ две точки

Причем векторыИ. неколлицеарны (рис. 4.6), то уравне-

Ние плоскости, проходящей через эту точку параллельно вектору а, имеет вид

(4-15)

Равенство (4.15) выражает необходимое и достаточное, условие компланарности трех векторов

- любая точка данной rmoikOtm

Уравнение плоскости, проходящей через данную точку и параллельной двум неколлннеарным векторам. Были даны два неколлинеарных вектора (рис. 4.7)И точка: то уравнение плос

Кости, проходящей через данную точку параллельно векторам а и Ь, имеет вид

(4.16)

Равенство (4.16) выражает необходимое и достаточное условие компланарности трех векторов:Где- произвольная точка данной плоскости.

41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки

Направляющим вектором прямой называется любой не нулевой вектор параллельный этой прямой.

Каноническое уравнение прямой в пространстве, проходящей через M0 (x0y0 z0) и имеющий направленный вектор а (а1 а2 а3)

х-х0= y-y0 = z-z0 (1)

а1a2 a3

Прямую линию в пространстве можно задать еще как результат пересечения плоскостей, т.е. систему уравнений

Если каждую из дробей равенства (1), обозначить через t, то путем алгебраических преобразований перейдем к параметрическому заданному уравнению прямой

x= x0 +a1t, y= y0+a2t, z=z0+a3t (2)

Если даны 2 точки М1 (x1y1z1) и М2(x2y2z2), то в качестве направляющего вектора, можно взять вектор

М1М2 = (x2-x1, y2-y1, z2-z1)

Поэтому равенство (1) примет вид

= =(3)

Которое называется уравнение прямой, проходящей через 2 точки.

43.Постоянные и переменные величины.Функциональнаязависимость.Понятие функции и основные способы ее задания. Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значения. Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения.2) Функциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает изменение другой.3)Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменнаяТабличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Преимущества табличного способа ~он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений.. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнениемАналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

studfiles.net

Уравнения плоскости проходящей через три точки

Пусть в координатном пространстве [cbm]Oxyz[/cbm] заданы три точки [cbm]M_0(x_0,y_0,z_0),[/cbm] [cbm]M_1(x_1,y_1,z_1),[/cbm] [cbm]M_2(x_2,y_2,z_2),[/cbm] не лежащие на одной прямой (рис.4.17). Требуется составить уравнение плоскости, проходящей через заданные точки.

Как было показано ранее (формула (1.23)), точка [cbm]M(x,y,z)[/cbm] принадлежит плоскости, проходящей через точки [cbm]M_0,[/cbm] [cbm]M_1,[/cbm] [cbm]M_2,[/cbm] тогда и только тогда, когда ее радиус-вектор [cbm]\overrightarrow{OM}[/cbm] удовлетворяет условию:

[cbm]\overrightarrow{OM}= (1-t_1-t_2)\cdot\overrightarrow{OM_0}+ t_1\cdot \overrightarrow{OM_1}+t_2\cdot\overrightarrow{OM_2}\,,[/cbm]

где [cbm]t_1,t_2[/cbm] - некоторые действительные числа (параметры). Это уравнение, а также его координатную форму

[cbm]\begin{cases} x=(1-t_1-t_2)\cdot x_0+t_1\cdot x_1+t_2\cdot x_2,\\ y=(1-t_1-t_2)\cdot y_0+t_1\cdot y_1+t_2\cdot y_2,\\ z=(1-t_1-t_2)\cdot z_0+t_1\cdot z_1+t_2\cdot z_2, \end{cases}[/cbm]

будем называть аффинным уравнением плоскости, проходящей через точки [cbm]M_0(x_0,y_0,z_0),[/cbm] [cbm]M_1(x_1,y_1,z_1),[/cbm] [cbm]M_2(x_2,y_2,z_2).[/cbm]

Используя векторы

[cbm]\vec{p}_1=\overrightarrow{M_0M_1}=(x_1-x_0)\vec{i}+(y_1-y_0)\vec{j}+(z_1-z_0)\vec{k}[/cbm]

и

[cbm]\vec{p}_2=\overrightarrow{M_0M_2}=(x_2-x_0)\vec{i}+(y_2-y_0)\vec{j}+(z_2-z_0)\vec{k}[/cbm]

в качестве направляющих векторов плоскости, составим уравнение вида (4.18):

[cbm]{\color{red}\boxed{{\color{black} \begin{vmatrix}x-x_0&y-y_0&z-z_0\\ x_1-x_0&y_1-y_0&z_1-z_0\\ x_2-x_0&y_2-y_0&z_2-z_0 \end{vmatrix}=0\,, }}}[/cbm]

(4.21)

которое называется уравнением плоскости, проходящей через три заданные точки.

Уравнение плоскости "в отрезках"

Пусть на координатных осях заданы точки [cbm]X_1(x_1,0,0),~Y_1(0,y_1,0)[/cbm] и [cbm]Z_1(0,0,z_1)[/cbm] , причем [cbm]x_1\ne0,[/cbm] [cbm]y_1\ne0,[/cbm] [cbm]z_1\ne0[/cbm] (рис.4.18). Требуется составить уравнение плоскости, проходящей через эти три точки.

Подставляя в уравнение (4.21) координаты заданных точек [cbm]X_1,\,Y_1,\,Z_1[/cbm] , получаем:

[cbm]\begin{vmatrix}x-x_1&y-0&z-0\\ 0-x_1&y_1-0&0-0\\ 0-x_1&0-0&z_1-0\end{vmatrix}= x\cdot y_1\cdot z_1+ x_1\cdot y\cdot z_1+ x_1\cdot y_1\cdot z- x_1\cdot y_1\cdot z_1=0.[/cbm]

Разделив уравнение на [cbm]x_1\cdot y_1\cdot z_1\ne0[/cbm] , получаем уравнение

[cbm]{\color{red}\boxed{{\color{black} \frac{x}{x_1}+\frac{y}{y_1}+\frac{z}{z_1}=1, \quad x_1\ne0,~y_1\ne0,~z_1\ne0, }}}[/cbm]

(4.22)

которое называется уравнением плоскости "в отрезках". Говорят, что плоскость, проходящая через точки [cbm]X_1(x_1,0,0),[/cbm] [cbm]Y_1(0,y_1,0)[/cbm] и [cbm]Z_1(0,0,z_1)[/cbm] , отсекает на координатных осях "отрезки": [cbm]x_1[/cbm] на оси абсцисс, [cbm]y_1[/cbm] на оси ординат и [cbm]z_1[/cbm] на оси аппликат. Разумеется, длины отрезков [cbm]OX_1,~OY_1[/cbm] и [cbm]OZ_1[/cbm] равны [cbm]|x_1|,~|y_1|[/cbm] и [cbm]|z_1|[/cbm] соответственно.

Замечания 4.5.

1. Перейти от общего уравнения плоскости (4.15) [cbm]Ax+By+Cz+D=0[/cbm] к уравнению "в отрезках" (4.22) можно при условии, что все коэффициенты общего уравнения отличны от нуля. Для этого нужно перенести свободный член в правую часть уравнения: [cbm]Ax+By+Cz=-D[/cbm] , а затем разделить обе части уравнения на [cbm]-D:[/cbm]

[cbm]\frac{A}{-D}\cdot x+\frac{B}{-D}\cdot y+\frac{C}{-D}\cdot z=1.[/cbm]

Обозначив [cbm]x_1=-\frac{A}{D},~y_1=-\frac{D}{B},~z_1=-\frac{D}{C}[/cbm] получим уравнение в отрезках (4.22):

[cbm]\frac{x}{x_1}\,+\,\frac{y}{y_1}\,+\,\frac{z}{z_1}\,=\,1.[/cbm]

2. Уравнения (4.21), (4.22), полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним, однако величины [cbm]|x_1|,~|y_1|[/cbm] и [cbm]|z_1|[/cbm] в общем случае не равны длинам отсекаемых отрезков [cbm]OX_1,~OY_1[/cbm] и [cbm]OZ_1[/cbm] .

Пример 4.9. В координатном пространстве [cbm]Oxyz[/cbm] (в прямоугольной системе координат) заданы точки [cbm]K(2,3,4),[/cbm] [cbm]L(6,-3,4),[/cbm] [cbm]M(-4,6,-4).[/cbm]

Требуется:

а) составить общее уравнение плоскости треугольника [cbm]KLM[/cbm] ;

б) составить уравнение в "отрезках" для плоскости треугольника [cbm]KLM[/cbm] ;

в) определить точки пересечения этой плоскости с координатными осями.

Решение. а) Составим уравнение (4.21):

[cbm]\begin{vmatrix}x-2&y-3&z-4\\6-2&-3-3&4-4\\-4-2&6-3&-4-4\end{vmatrix}=0 \quad \Leftrightarrow \quad \begin{vmatrix}x-2&y-3&z-4\\4&-6&0\\-6&63&-8\end{vmatrix}=0[/cbm]

Раскрывая определитель и приводя подобные члены, получаем

[cbm]48\cdot (x-2)+ 32\cdot(y-3) -24\cdot(z-4)=0 \quad\Leftrightarrow\quad 6x+4y-3z-12=0.[/cbm]

б) Переносим свободный член общего уравнения плоскости (см. пункт "а") в правую часть и делим уравнение на 12, получаем уравнение плоскости в "отрезках":

[cbm]\frac{x}{2}+\frac{y}{3}-\frac{z}{4}=1.[/cbm]

в) По уравнению плоскости в "отрезках" заключаем, что плоскость (см. пункт "б") проходит через точки [cbm]X(2,0,0),[/cbm] [cbm]Y(0,3,0),[/cbm] [cbm]Z(0,0,-4)[/cbm] на координатных осях.

В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Источник

calcsbox.com

Уравнение плоскости, проходящей через три точки — Циклопедия

Аналитическая геометрия

Уравнение плоскости, проходящей через три точки, задаётся равенством нулю смешанного произведения векторов разностей радиусов-векторов точек (кроме одной) и радиус-вектора одной точки.

Введём обозначения:

[math]\bar r=(x,y,z)[/math] — радиус-вектор точки плоскости;

[math]\bar r_1=(x_1,y_1,z_1)[/math] — радиус-вектор первой точки;

[math]\bar r_2=(x_2,y_2,z_2)[/math] — радиус-вектор второй точки;

[math]\bar r_3=(x_3,y_3,z_3)[/math] — радиус-вектор третьей точки.

Векторная форма:

Координатная форма:

[править] Уравнения плоскости:

[править] Другие уравнения:

cyclowiki.org