Как описать окружность около прямоугольного треугольника. Как вокруг прямоугольного треугольника описать окружность
Окружность, описанная около прямоугольного треугольника
Определение и формулы описанной окружности прямоугольного треугольника
ОПРЕДЕЛЕНИЕОкружность, описанная около треугольника, содержит все вершины треугольника.
Центр описанной окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
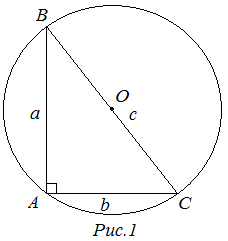
Рассмотрим прямоугольный треугольник  . Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус описанной окружности равен половине гипотенузы
. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус описанной окружности равен половине гипотенузы
![Rendered by QuickLaTeX.com \[R=\frac{c}{2} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-74aa58a88b5bbe2ca870b6aacd7338d5_l3.png)
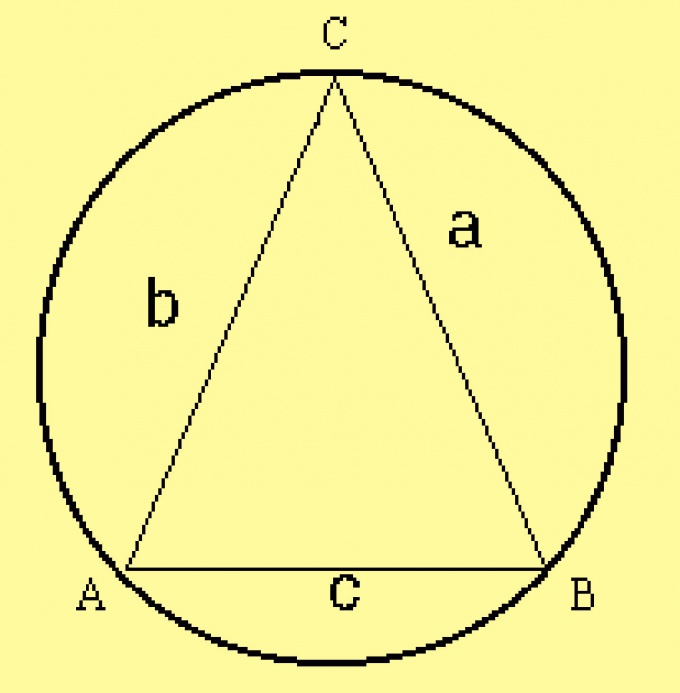
Для прямоугольного треугольника справедлива теорема синусов:
![Rendered by QuickLaTeX.com \[\frac{a}{\sin \alpha } =\frac{b}{\sin \beta } =c=2R,\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-41a6d0e68232ebab22da29a2700112be_l3.png)
где 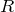 – радиус описанной около прямоугольного треугольника окружности,
– радиус описанной около прямоугольного треугольника окружности, 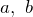 – катеты этого треугольника,
– катеты этого треугольника,  – его гипотенуза,
– его гипотенуза, 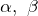
Примеры решения задач
ПРИМЕР 2| Задание | В прямоугольном треугольнике медиана 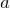 , проведенная к гипотенузе, делит прямой угол в отношении , проведенная к гипотенузе, делит прямой угол в отношении 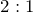 . Найти катеты треугольника. . Найти катеты треугольника.
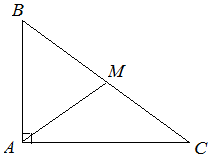 |
| Решение | Рассмотрим прямоугольный треугольник 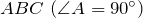 и проведем медиану и проведем медиану 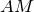 . Так как центр окружности, описанной около прямоугольного треугольника, находится на середине гипотенузы, то медиана . Так как центр окружности, описанной около прямоугольного треугольника, находится на середине гипотенузы, то медиана 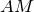 является радиусом описанной окружности и является радиусом описанной окружности и
Пусть Отсюда получаем, что Поскольку А это означает, что |
| Ответ | 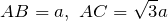 |

| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Как описать окружность около прямоугольного треугольника
Треугольник — простейшая из плоских многоугольных фигур. Если величина какого-нибудь угла в его вершинах равна 90°, то треугольник именуется прямоугольным. Около такого многоугольника дозволено начертить круг таким методом, дабы всякая из 3 вершин имела одну всеобщую точку с его рубежом (окружностью). Эта окружность будет именоваться описанной, а присутствие прямого угла гораздо упрощает задачу ее построения.
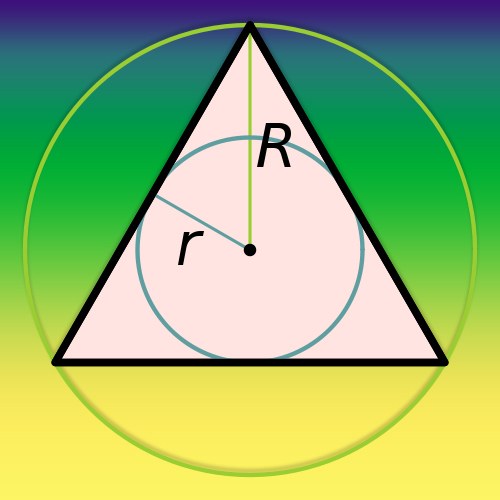
Вам понадобится
- Линейка, циркуль, калькулятор.
Инструкция
1. Начните с определения радиуса окружности, которую нужно будет возвести. Если есть вероятность измерить длины сторон треугольника, то обратите внимание на его гипотенузу — сторону, лежащую наоборот прямого угла. Измерьте ее и поделите полученное значение напополам — это и будет радиус описываемой около прямоугольного треугольника окружности.
2. Если длина гипотенузы неведома, но есть длины (a и b) катетов (2-х сторон, прилегающих к прямому углу), то радиус (R) обнаружьте с применением теоремы Пифагора. Из нее вытекает, что данный параметр будет равен половине квадратного корня, извлеченного из суммы возведенных в квадрат длин катетов: R=?*?(a?+b?).
3. Если вестима длина лишь одного из катетов (a) и величина прилегающего к нему острого угла (?), то для определения радиуса описанной окружности (R) используйте тригонометрическую функцию — косинус. В прямоугольном треугольнике она определяет соотношение длин гипотенузы и этого катета. Рассчитайте половину частного от деления длины катета на косинус знаменитого угла: R=?*a/cos(?).
4. Если помимо длины одного из катетов (a) вестима величина острого угла (?), лежащего наоборот него, то для вычисления радиуса (R) воспользуйтесь иной тригонометрической функцией — синусом. Помимо замены функции и стороны в формуле ничего не изменится — поделите длину катета на синус вестимого острого угла, а итог поделите напополам: R=?*b/sin(?).
5. Позже нахождения радиуса любым из перечисленных методов определите центр описываемой окружности. Для этого отложите на циркуле полученное значение и установите его в всякую вершину треугольника. Описывать полный круг нет необходимости, легко подметьте место его пресечения с гипотенузой — эта точка и будет центром окружности. Таково качество прямоугольного треугольника — центр описанной около него окружности неизменно находится в середине его самой длинной стороны. Начертите круг отложенного на циркуле радиуса с центром в обнаруженной точке. На этом построение будет закончено.
Изредка около выпуклого многоугольника дозволено начертить окружность таким образом, дабы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику нужно называть описанной. Ее центр не непременно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , обнаружить эту точку, как водится, не дюже сложно.
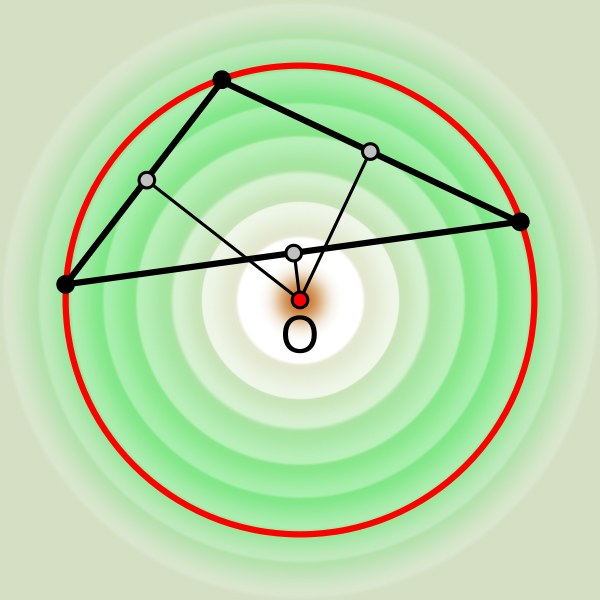
Вам понадобится
- Линейка, карандаш, транспортир либо угольник, циркуль.
Инструкция
1. Если многоугольник, около которого необходимо описать окружность, начерчен на бумаге, для нахождения центр а круга довольно линейки, карандаша и транспортира либо угольника. Измерьте длину всякий из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С поддержкой угольника либо транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
2. Проделайте эту же операцию с всякий иной стороной многоугольника. Пересечение 2-х построенных отрезков и будет желанной точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым числом сторон неизменно лежит в точке пересечения серединных перпендикуляров, проведенных к этим сторонам.
3. Для верных многоугольников определение центр а вписанной окружности может быть гораздо проще. Скажем, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В положительном многоугольнике с любым четным числом сторон довольно объединить вспомогательными отрезками две пары лежащих друг наоборот друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи легко определите середину самой длинной стороны фигуры — гипотенузы.
4. Если из условий незнакомо, дозволено ли в тезисе начертить описанную окружность для данного многоугольника, позже определения полагаемой точки центр а любым из описанных методов вы можете это узнать. Отложите на циркуле расстояние между обнаруженной точкой и всякий из вершин, установите циркуль в полагаемый центр окружности и начертите круг — вся вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из основных свойств и описать окружность около данного многоугольника невозможно.
Согласно определению, описанная окружность должна проходить через все вершины углов заданного многоугольника. При этом идеально неважно, что это за многоугольник — треугольник, квадрат, прямоугольник, трапеция либо что-то иное. Также не играет роли, верный либо неверный это многоугольник. Нужно лишь рассматривать, что существуют многоугольники, вокруг которых окружность описать невозможно. Неизменно дозволено описать окружность вокруг треугольника. Что касается четырехугольников, то окружность дозволено описать около квадрата либо прямоугольника либо равнобедренной трапеции.

Вам понадобится
- Заданный многоугольника
- Линейка
- Угольник
- Карандаш
- Циркуль
- Транспортир
- Таблицы синусов и косинусов
- Математические представления и формулы
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
- Признаки подобия треугольников
Инструкция
1. Постройте многоугольник с заданными параметрами и определите, дозволено ли описать вокруг него окружность . Если вам дан четырехугольник, посчитайте суммы его противоположных углов. Всякая из них должна равняться 180°.
2. Для того, дабы описать окружность , необходимо вычислить ее радиус. Припомните, где лежит центр описанной окружности в различных многоугольниках. В треугольнике он находится в точке пересечения всех высот данного треугольника. В квадрате и прямоугольники — в точке пересечения диагоналей, для трапеции- в точке пересечения оси симметрии к линии, соединяющей середины боковых сторон, а для всякого иного выпуклого многоугольника — в точке пересечения серединных перпендикуляров к сторонам.
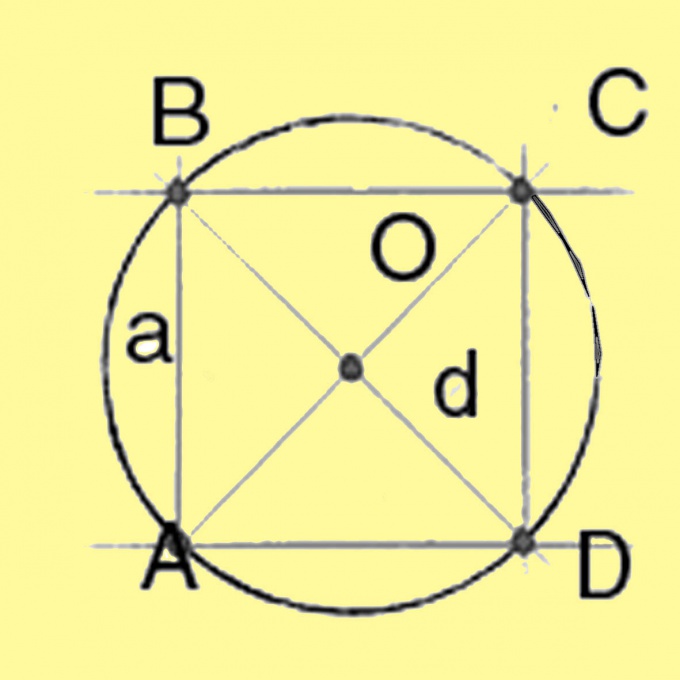
3. Диаметр окружности, описанной вокруг квадрата и прямоугольника, вычислите по теореме Пифагора. Он будет равняться квадратному корню из суммы квадратов сторон прямоугольника. Для квадрата, у которого все стороны равны, диагональ равна квадратному корню из удвоенного квадрата стороны. Поделив диаметр на 2, получаете радиус.
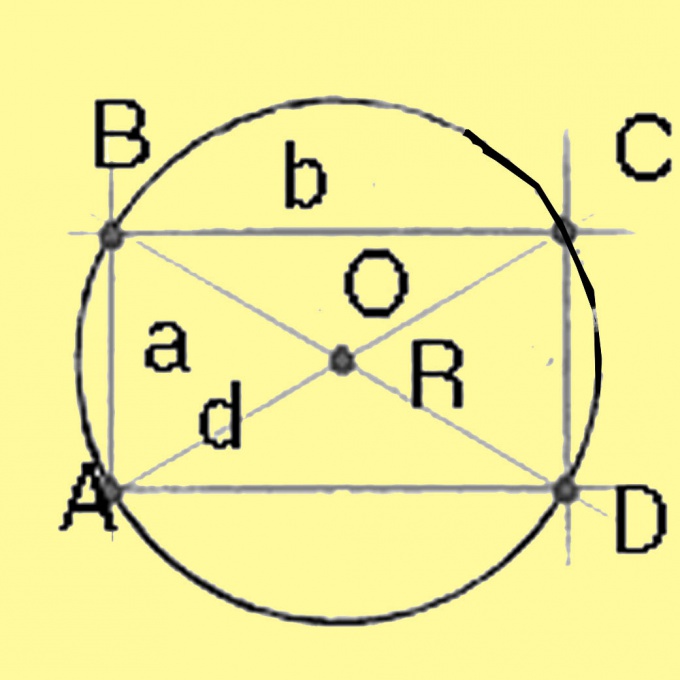
4. Вычислите радиус описанной окружности для треугольника. От того что параметры треугольника заданы в условиях, вычислите радиус по формуле R = a/(2·sinA), где а — одна из сторон треугольника, ? — противолежащий ей угол. Взамен этой стороны дозволено взять всякую иную сторону и противолежащий ей угол.
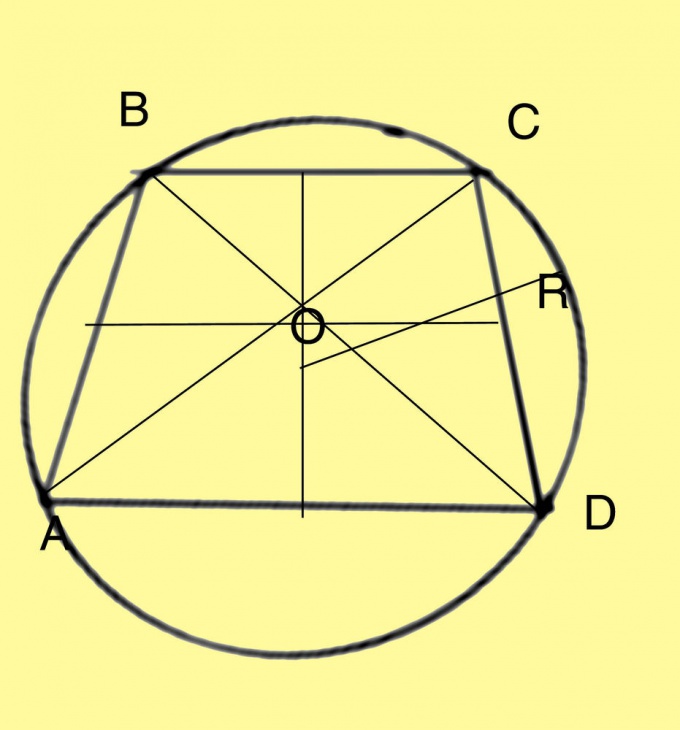
5. Вычислите радиус окружности, описанной вокруг трапеции. R = a*d*c / 4 v(p*(p-a)*(p-d)*(p-c)) В этой формуле a и b — вестимые по условиям задания основания трапеции, h — высота, d — диагональ, p = 1/2*(a+d+c) . Вычислите недостающие значения. Высоту дозволено вычислить по теореме синусов либо косинусов, от того что длины сторон трапеции и углы заданы в условиях задачи. Зная высоту и рассматривая знаки подобия треугольников, вычислите диагональ. Позже этого останется только вычислить радиус по указанной выше формуле.
Видео по теме
Полезный совет Дабы вычислить радиус окружности, описанной вокруг иного многоугольника, исполните ряд дополнительных построений. Получите больше примитивные фигуры, параметры которых вам знамениты.
Прямоугольным называют треугольник, угол в одной из вершин которого равен 90°. Сторону, лежащую наоборот этого угла, называют гипотенузой, а стороны, противолежащие двум острым углам треугольника, именуются катетами. Если знаменита длина гипотенузы и величина одного из острых углов, то этих данных довольно, чтоб возвести треугольник, как минимум, двумя методами.

Вам понадобится
- Лист бумаги, карандаш, линейка, циркуль, калькулятор.
Инструкция
1. 1-й метод требует наличия помимо карандаша и бумаги еще и линейки, транспортира и угольника. Вначале начертите ту сторону, которая является гипотенузой — поставьте точку A, отложите от нее вестимую длину гипотенузы, поставьте точку С и объедините точки.
2. Приложите транспортир к проведенному отрезку таким образом, дабы нулевая отметка совпала с точкой A, отмерьте величину вестимого острого угла и поставьте вспомогательную точку. Проведите линию, которая будет начинаться в точке A и проходить через вспомогательную точку.
3. Приложите угольник к отрезку AC таким образом, дабы прямой угол начинался от точки C. Точку пересечения угольником линии, проведенной на предыдущем шаге, обозначьте буквой B и объедините ее с точкой C. На этом построение прямоугольного треугольника с знаменитой длиной стороны AC (гипотенузы) и острым углом в вершине A будет завершено.
4. Иной метод помимо карандаша и бумаги затребует наличия линейки, циркуля и калькулятора. Начните с вычисления длин катетов — умения величины одного острого угла и длины гипотенузы для этого абсолютно довольно.
5. Рассчитайте длину того катета (AB), тот, что лежит наоборот угла вестимой величины (β) — он будет равен произведению длины гипотенузы (AC) на синус знаменитого угла AB=AC*sin(β).
6. Определите длину иного катета (BC) — она будет равна произведению длины гипотенузы на косинус вестимого угла BC=AC*cos(β).
7. Поставьте точку A, отмерьте от нее длину гипотенузы, поставьте точку C и проведите между ними линию.
8. Отложите на циркуле длину катета AB, рассчитанную в пятом шаге и начертите вспомогательный полукруг с центром в точке A.
9. Отложите на циркуле длину катета BC, рассчитанную в шестом шаге и начертите вспомогательный полукруг с центром в точке С.
10. Подметьте точку пересечения 2-х полукругов буквой B и проведите отрезки между точками A и B, C и B. На этом построение прямоугольного треугольника будет закончено.
Ошеломительными свойствами прямоугольных треугольников люди заинтересовались еще во времена древности. Многие из этих свойств были описаны древнегреческим ученым Пифагором. В Старинной Греции возникли и наименования сторон прямоугольного треугольника.
Какой треугольник называют прямоугольным?
Есть несколько типов треугольников. У одних все углы острые, у других – один тупой и два острых, у третьих – два острых и прямой. По этому знаку всякий тип этих геометрических фигур и получил наименование: остроугольные, тупоугольные и прямоугольные. То есть, прямоугольным именуется такой треугольник, у которого один из углов составляет 90°. Есть и другое определение, аналогичное с первым. Прямоугольным именуется треугольник, у которого две стороны перпендикулярны.
Гипотенуза и катеты
У остроугольного и тупоугольного треугольников отрезки, соединяющие вершины углов, именуются примитивно сторонами. У треугольника прямоугольного стороны имеют и другие наименования. Те, которые прилегают к прямому углу, именуются катетами. Сторона, противолежащая прямому углу, именуется гипотенузой. В переводе с греческого слово «гипотенуза» обозначает «натянутая», а «катет» — «перпендикуляр».
Соотношения между гипотенузой и катетами
Стороны прямоугольного треугольника связаны между собой определенными соотношениями, которые гораздо облегчают вычисления. Скажем, зная размеры катетов, дозволено вычислить длину гипотенузы. Это соотношение по имени открывшего его математика получило наименование теоремы Пифагора и выглядит оно так:c2=a2+b2, где с – гипотенуза, a и b – катеты. То есть, гипотенуза будет равна квадратному корню из суммы квадратов катетов. Дабы обнаружить всякий из катетов, довольно из квадрата гипотенузы вычесть квадрат иного катета и извлечь из полученной разности квадратный корень.
Прилежащий и противолежащий катет
Начертите прямоугольный треугольник АСВ. Буквой С принято обозначать вершину прямого угла, А и В – вершины острых углов. Стороны, противолежащие всему углу, комфортно назвать а, b и с, по наименованиям лежащих наоборот них углов. Разглядите угол А. Катет а для него будет противолежащим, катет b – прилежащим. Отношение противолежащего катета к гипотенузе именуется синусом. Вычислить эту тригонометрическую функцию дозволено по формуле: sinA=a/c. Отношение прилежащего катета к гипотенузе именуется косинусом. Вычисляется он по формуле: cosA=b/c. Таким образом, зная угол и одну из сторон, дозволено по этим формулам вычислить иную сторону. Тригонометрическими соотношениями связаны и оба катета. Отношение противолежащего к прилежащему именуется тангенсом, а прилежащего к противолежащему – котангенсом. Выразить эти соотношения дозволено формулами tgA=a/b либо ctgA=b/a.
jprosto.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике - Планиметрия

Серединный перпендикуляр к отрезку
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.

Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,


Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,


Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.

Рис.5
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикулярык сторонам треугольника |  | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.Посмотреть доказательство |
| Окружность, описанная около треугольника |  | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  | Для любого треугольника справедливы равенства (теорема синусов):
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |  | Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |  | Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Серединные перпендикуляры к сторонам треугольника |
 Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |
 Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности |
 Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
 Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |
 Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
 Для любого треугольника справедливы равенства (теорема синусов):
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |
 Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |
 Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 6).

Рис.6
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
CO = AO .
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
AO = BO .
Следовательно, справедливо равенство:
CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
AO = OB = OC ,
из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)

Рис.7
справедливы равенства:
 .
.
Доказательство. Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R, на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Рис.8
Угол MPN, как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):


Теорема синусов доказана.

На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Окружность описанная около прямоугольного треугольника

Окружность описанная около прямоугольного треугольника. В этой публикации мы с вами рассмотрим доказательство одного «математического факта», который широко используется при решении задач по геометрии. В одних источниках сей факт обозначается как теорема, в других как свойство, формулировки имеются разные, но суть их одна:

Любой треугольник построенный на диаметре окружности, третья вершина которого лежит на этой окружности является прямоугольным!
То есть закономерность в этом геометрическом узоре состоит в том, что, куда бы вы ни поместили вершину треугольника, угол при этой вершине всегда будет прямым:

Заданий присутствующих с составе экзамена по математике, в ходе решений которых используется это свойство, достаточно много.
Стандартное доказательство считаю весьма путанным и перегруженным математическими символами, его вы найдёте в учебнике. Мы же рассмотрим простое и интуитивно понятное. Его я обнаружил в одном замечательном эссе под названием "Плач математика", рекомендую к прочтению учителям и ученикам.
Сначала вспомним некоторые теоретические моменты:
Признак параллелограмма. У параллелограмма противолежащие стороны равны. То есть если у четырехугольника обе пары противолежащих сторон равны, то этот четырехугольник – параллелограмм.
Признак прямоугольника. Прямоугольник является параллелограммом, и его диагонали равны. То есть если у параллелограмма диагонали равны, то он является прямоугольником.
*Прямоугольник является параллелограммом, это его частный случай.
Итак, приступим:
Возьмем треугольник и относительно центра окружности повернем его на 1800 (перевернём его). У нас получится четырехугольник, вписанный в окружность:

Поскольку мы просто повернули треугольник, то противолежащие стороны четырехугольника равны, значит это параллелограмм. Поскольку треугольник повернут ровно на 180 градусов, значит его вершина диаметрально противоположна вершине «исходного» треугольника.
Получается, что диагонали четырёхугольника равны, так они являются диаметрами. Имеем четырёхугольник у которого противолежащие стороны равны и диагонали равны, следовательно это есть прямоугольник, а у него все углы прямые.
Вот и всё доказательство!
Можно рассмотреть и такое, тоже простое и понятное:
Посмотреть ещё одно доказательство =>>
Из точки С построим отрезок проходящий через центр окружности, другой конец которого будет лежать на противоположной точке окружности (точка D). Точку D соединим с вершинами А и В: Получили четырёхугольник. Треугольник АОD равен треугольнику СОВ по двум сторонам и углу между ними:
Получили четырёхугольник. Треугольник АОD равен треугольнику СОВ по двум сторонам и углу между ними:

Из равенства треугольников следует, что AD = CB.
Аналогично и АС = DB.
Можем сделать вывод, что четырёхугольник является параллелограммом. Кроме того, его диагонали равны – АВ изначально дан как диаметр, СD также диаметр (проходит через точку О).
Таким образом, АСВD прямоугольник, значит все его углы прямые. Доказано!
Ещё один примечательный подход, который ярко и «красиво» говорит нам о том, что рассматриваемый угол всегда прямой.
Посмотрите и вспомните информацию про вписанный угол. А теперь посмотрите на эскиз:

Угол АОВ не что иное как центральный угол опирающийся на дугу АDB, и равен он 180 градусам. Да, АВ это диаметр окружности, но ничто нам не мешает считать АОВ центральным углом (это развёрнутый угол). Угол же АСВ является вписанным для него, он опирается также же дугу на АDB.
А мы знаем, что вписанный угол равен половине центрального, то есть как бы мы не разместили точку С на окружности, угол АСВ всегда будет равен 90 градусам, то является прямым.
Какие выводы можно сделать применительно к решению задач, в частности включённых в экзамен?
Если в условии речь идёт о треугольнике вписанном в окружность и построенном на диаметре этой окружности, то однозначно этот треугольник является прямоугольным.
Если сказано, что прямоугольный треугольник вписан в окружность, то это означает, что его гипотенуза является совпадает с её диаметром (равна ему) и центр гипотенузы совпадает с центром окружности.
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях.
matematikalegko.ru
Как описать окружность около прямоугольного треугольника
Треугольник - простейшая из плоских многоугольных фигур. Если величина какого-либо угла в его вершинах равна 90°, то треугольник называется прямоугольным. Около такого многоугольника можно начертить круг таким способом, чтобы каждая из трех вершин имела одну общую точку с его границей (окружностью). Эта окружность будет называться описанной, а наличие прямого угла значительно упрощает задачу ее построения.Вам понадобится
- Линейка, циркуль, калькулятор.
Инструкция
- Начните с определения радиуса окружности, которую надо будет построить. Если есть возможность измерить длины сторон треугольника, то обратите внимание на его гипотенузу - сторону, лежащую напротив прямого угла. Измерьте ее и разделите полученное значение пополам - это и будет радиус описываемой около прямоугольного треугольника окружности.
- Если длина гипотенузы неизвестна, но есть длины (a и b) катетов (двух сторон, прилегающих к прямому углу), то радиус (R) найдите с использованием теоремы Пифагора. Из нее вытекает, что этот параметр будет равен половине квадратного корня, извлеченного из суммы возведенных в квадрат длин катетов: R=½*√(a²+b²).
- Если известна длина лишь одного из катетов (a) и величина прилегающего к нему острого угла (β), то для определения радиуса описанной окружности (R) используйте тригонометрическую функцию - косинус. В прямоугольном треугольнике она определяет соотношение длин гипотенузы и этого катета. Рассчитайте половину частного от деления длины катета на косинус известного угла: R=½*a/cos(β).
- Если кроме длины одного из катетов (a) известна величина острого угла (α), лежащего напротив него, то для вычисления радиуса (R) воспользуйтесь другой тригонометрической функцией - синусом. Кроме замены функции и стороны в формуле ничего не изменится - разделите длину катета на синус известного острого угла, а результат поделите пополам: R=½*b/sin(α).
- После нахождения радиуса любым из перечисленных способов определите центр описываемой окружности. Для этого отложите на циркуле полученное значение и установите его в любую вершину треугольника. Описывать полный круг нет необходимости, просто отметьте место его пресечения с гипотенузой - эта точка и будет центром окружности. Таково свойство прямоугольного треугольника - центр описанной около него окружности всегда находится в середине его самой длинной стороны. Начертите круг отложенного на циркуле радиуса с центром в найденной точке. На этом построение будет завершено.
completerepair.ru
Как описать окружность вокруг треугольника
Треугольник считается вписанным в окружность , если все его вершины лежат на ней. Окружность дозволено описать вокруг всякого треугольника , и притом только одну. Как же обнаружить центр этой окружности и ее диаметр?

Вам понадобится
- — линейка;
- — карандаш;
- — циркуль.
Инструкция
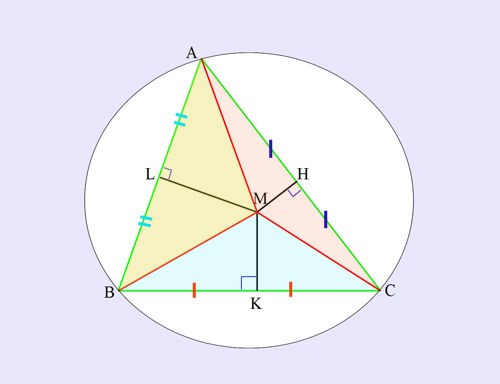
1. По теореме центром описанной окружности является центр пересечения серединных перпендикуляров. На рисунке видно, что всякая сторона треугольника , перпендикуляр, проведенный из ее середины и отрезки, соединяющие точку пересечения перпендикуляров с вершинами, образуют два равных прямоугольных треугольника . Отрезки MА, MВ, MС равны.
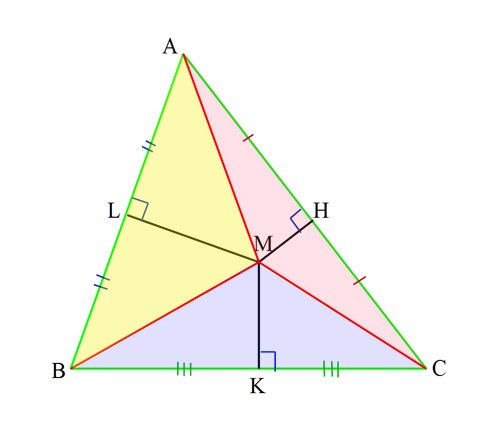
2. Вам дан треугольник. Обнаружьте середину всей стороны – возьмите линейку и измерьте его стороны. Полученные размеры поделите напополам. Отложите от вершин на всей стороне половину ее размера. Подметьте итоги точками.
3. Из всякой точки отложите перпендикуляр к стороне. Точка пересечения этих перпендикуляров будет центром описанной окружности. Для нахождения центра окружности довольно 2-х перпендикуляров. 3-й строится для самопроверки.
4. Обратите внимание – в треугольнике, где все углы острые, точка пересечения находится внутри треугольника . В прямоугольном треугольнике – лежит на гипотенузе. В тупоугольном – находится за его пределами. Причем перпендикуляр к стороне наоборот тупого угла построен не к центру треугольника , а наружу.
5. Измерьте расстояние от точки пересечения перпендикуляров до всякий вершины треугольника . Установите это значение на циркуле. Разместив иглу в точку пересечения, начертите окружность . Если она касается всех 3 вершин треугольника , вы все сделали верно.
Согласно определению, описанная окружность должна проходить через все вершины углов заданного многоугольника. При этом идеально неважно, что это за многоугольник — треугольник, квадрат, прямоугольник, трапеция либо что-то иное. Также не играет роли, верный либо неверный это многоугольник. Нужно лишь рассматривать, что существуют многоугольники, вокруг которых окружность описать невозможно. Неизменно дозволено описать окружность вокруг треугольника. Что касается четырехугольников, то окружность дозволено описать около квадрата либо прямоугольника либо равнобедренной трапеции.

Вам понадобится
- Заданный многоугольника
- Линейка
- Угольник
- Карандаш
- Циркуль
- Транспортир
- Таблицы синусов и косинусов
- Математические представления и формулы
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
- Признаки подобия треугольников
Инструкция
1. Постройте многоугольник с заданными параметрами и определите, дозволено ли описать вокруг него окружность . Если вам дан четырехугольник, посчитайте суммы его противоположных углов. Всякая из них должна равняться 180°.
2. Для того, дабы описать окружность , надобно вычислить ее радиус. Припомните, где лежит центр описанной окружности в различных многоугольниках. В треугольнике он находится в точке пересечения всех высот данного треугольника. В квадрате и прямоугольники — в точке пересечения диагоналей, для трапеции- в точке пересечения оси симметрии к линии, соединяющей середины боковых сторон, а для всякого иного выпуклого многоугольника — в точке пересечения серединных перпендикуляров к сторонам.

3. Диаметр окружности, описанной вокруг квадрата и прямоугольника, вычислите по теореме Пифагора. Он будет равняться квадратному корню из суммы квадратов сторон прямоугольника. Для квадрата, у которого все стороны равны, диагональ равна квадратному корню из удвоенного квадрата стороны. Поделив диаметр на 2, получаете радиус.

4. Вычислите радиус описанной окружности для треугольника. От того что параметры треугольника заданы в условиях, вычислите радиус по формуле R = a/(2·sinA), где а — одна из сторон треугольника, ? — противолежащий ей угол. Взамен этой стороны дозволено взять всякую иную сторону и противолежащий ей угол.

5. Вычислите радиус окружности, описанной вокруг трапеции. R = a*d*c / 4 v(p*(p-a)*(p-d)*(p-c)) В этой формуле a и b — вестимые по условиям задания основания трапеции, h — высота, d — диагональ, p = 1/2*(a+d+c) . Вычислите недостающие значения. Высоту дозволено вычислить по теореме синусов либо косинусов, от того что длины сторон трапеции и углы заданы в условиях задачи. Зная высоту и рассматривая знаки подобия треугольников, вычислите диагональ. Позже этого останется только вычислить радиус по указанной выше формуле.

Видео по теме
Полезный совет Дабы вычислить радиус окружности, описанной вокруг иного многоугольника, исполните ряд дополнительных построений. Получите больше примитивные фигуры, параметры которых вам знамениты.
Прямоугольным называют треугольник, угол в одной из вершин которого равен 90°. Сторону, лежащую наоборот этого угла, называют гипотенузой, а стороны, противолежащие двум острым углам треугольника, именуются катетами. Если знаменита длина гипотенузы и величина одного из острых углов, то этих данных довольно, чтоб возвести треугольник, как минимум, двумя методами.

Вам понадобится
- Лист бумаги, карандаш, линейка, циркуль, калькулятор.
Инструкция
1. 1-й метод требует наличия помимо карандаша и бумаги еще и линейки, транспортира и угольника. Вначале начертите ту сторону, которая является гипотенузой — поставьте точку A, отложите от нее знаменитую длину гипотенузы, поставьте точку С и объедините точки.
2. Приложите транспортир к проведенному отрезку таким образом, дабы нулевая отметка совпала с точкой A, отмерьте величину знаменитого острого угла и поставьте вспомогательную точку. Проведите линию, которая будет начинаться в точке A и проходить через вспомогательную точку.
3. Приложите угольник к отрезку AC таким образом, дабы прямой угол начинался от точки C. Точку пересечения угольником линии, проведенной на предыдущем шаге, обозначьте буквой B и объедините ее с точкой C. На этом построение прямоугольного треугольника с вестимой длиной стороны AC (гипотенузы) и острым углом в вершине A будет завершено.
4. Иной метод помимо карандаша и бумаги затребует наличия линейки, циркуля и калькулятора. Начните с вычисления длин катетов — умения величины одного острого угла и длины гипотенузы для этого абсолютно довольно.
5. Рассчитайте длину того катета (AB), тот, что лежит наоборот угла знаменитой величины (β) — он будет равен произведению длины гипотенузы (AC) на синус вестимого угла AB=AC*sin(β).
6. Определите длину иного катета (BC) — она будет равна произведению длины гипотенузы на косинус знаменитого угла BC=AC*cos(β).
7. Поставьте точку A, отмерьте от нее длину гипотенузы, поставьте точку C и проведите между ними линию.
8. Отложите на циркуле длину катета AB, рассчитанную в пятом шаге и начертите вспомогательный полукруг с центром в точке A.
9. Отложите на циркуле длину катета BC, рассчитанную в шестом шаге и начертите вспомогательный полукруг с центром в точке С.
10. Подметьте точку пересечения 2-х полукругов буквой B и проведите отрезки между точками A и B, C и B. На этом построение прямоугольного треугольника будет закончено.
Обратите внимание! Существует теорема синусов, устанавливающая связанность между сторонами треугольника, его углами и радиусами описанной окружности. Эта связанность выражается формулой: a/sina = b/sinb = с/sinc = 2R, где a, b, c – стороны треугольника; sina, sinb, sinc – синусы углов, противолежащих этим сторонам; R – радиус окружности, которую дозволено описать вокруг треугольника.
jprosto.ru
Описанная окружность вокруг прямоугольного треугольника
Высота бака цилиндрической формы равна 20см,а площадь его основания 150 квадратных см.Чему равен объем этого бака(в литрах)? в одном литре 1000 кубических сантиметров., Математика, 10 — 11 классы.
Описанная окружность вокруг прямоугольного треугольника
Программа предназначена для определения радиуса описанной вокруг прямоугольного треугольника окружности.
Окружность называется описанной вокруг прямоугольного треугольника, в том случае, если все вершины прямоугольного треугольника лежат на этой окружности.
Вокруг прямоугольного треугольника можно описать лишь одну окружность.
Формула для вычисления радиуса описанной вокруг прямоугольного треугольника окружности:
Где a, b — стороны треугольника.
Следует отметить, что диаметр описанной вокруг прямоугольного треугольника окружности равен гипотенузе прямоугольного треугольника.
Чтобы найти радиус и диаметр описанной вокруг прямоугольного треугольника окружности, введите значения катетов a и b прямоугольного треугольника и нажмите кнопку «ВЫЧИСЛИТЬ».
Результатом вычислений будет радиус и диаметр описанной вокруг прямоугольного треугольника окружности.
Описанная окружность вокруг прямоугольного треугольника
Описанная окружность вокруг прямоугольного треугольника
Программа предназначена для определения радиуса описанной вокруг прямоугольного треугольника окружности.
Окружность называется описанной вокруг прямоугольного треугольника, в том случае, если все вершины прямоугольного треугольника лежат на этой окружности.
Вокруг прямоугольного треугольника можно описать лишь одну окружность.
Формула для вычисления радиуса описанной вокруг прямоугольного треугольника окружности:
Где a, b — стороны треугольника.
Следует отметить, что диаметр описанной вокруг прямоугольного треугольника окружности равен гипотенузе прямоугольного треугольника.
Чтобы найти радиус и диаметр описанной вокруг прямоугольного треугольника окружности, введите значения катетов a и b прямоугольного треугольника и нажмите кнопку «ВЫЧИСЛИТЬ».
Результатом вычислений будет радиус и диаметр описанной вокруг прямоугольного треугольника окружности.
Описанная окружность вокруг прямоугольного треугольника
Окружность, описанная около треугольника
Что такое окружность, описанная около треугольника? Что является центром этой окружности? Как расположение центра описанной окружности зависит от вида треугольника?
Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.
При этом треугольник называется вписанным в окружность.
Расстояние от любой вершины треугольника до центра описанной окружности равно радиусу этой окружности.
Окружность можно описать около любого треугольника.
Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника (то есть отрезков, перпендикулярных к сторонам треугольника и проходящих через середины этих сторон).
Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (напротив тупого угла, за большей стороной).

poiskvstavropole.ru

![Rendered by QuickLaTeX.com \[AM=BM=MC=a\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1908329a3d00e20e6300fd235ab31ad8_l3.png)
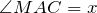 , тогда из условия задачи следует, что
, тогда из условия задачи следует, что 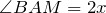 и
и ![Rendered by QuickLaTeX.com \[x+2x=90^{\circ} \Rightarrow 3x=90^{\circ} \Rightarrow x=30^{\circ} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-124c085782a519584f2bdbe82ba74c82_l3.png)
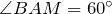 .
. 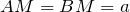 , то
, то 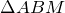 – равнобедренный, а значит
– равнобедренный, а значит 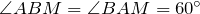 и
и ![Rendered by QuickLaTeX.com \[\angle BMA=180^{\circ} -120^{\circ} =60^{\circ} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-46ffb9cfc5e53c50423a710a204af5e1_l3.png)
 . Тогда по теореме Пифагора
. Тогда по теореме Пифагора![Rendered by QuickLaTeX.com \[AC=\sqrt{BC^{2} -AB^{2}} =\sqrt{\left(2a\right)^{2} -a^{2}} =\sqrt{4a^{2} -a^{2}} =\sqrt{3} a\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7bd66e27cd2a81e7ba994c8d072b8ca7_l3.png)










