Касательная к графику функции Уравнение касательной Геометрический. Касательная к графику функции это
Касательная к графику функции | Учеба-Легко.РФ
Рассмотрим следующий рисунок:
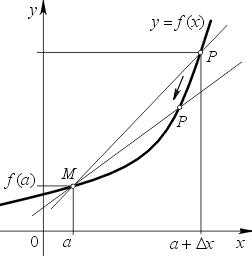
На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.
Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.
Касательная к графику функции
Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существуеткасательная к нему.
При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f - это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Уравнение касательной
Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:
y = k*x + b.
Так как у нас угловой коэффициент равен производной f’(x0), то уравнение примет следующий вид: y = f’(x0)*x + b.
Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.
f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) – f’(x0)*x0.
Подставляем полученное значение в уравнение касательной:
y = f’(x0)*x + b = f’(x0)*x + f(x0) – f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).
y = f(x0) + f’(x0)*(x - x0).
Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x3 – 2*x2 + 1 в точке х = 2.
1. х0 = 2.
2. f(x0) = f(2) = 22 - 2*22 + 1 = 1.
3. f’(x) = 3*x2 – 4*x.
4. f’(x0) = f’(2) = 3*22 – 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x - 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x - 7.
Ответ: y = 4*x - 7.
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
4. Вычислить f’(x0)
5. Подставить полученные значения в уравнение касательной y= f(x0) + f’(x0)*(x - x0).
uclg.ru
[Зачет 85] Определение производной функции в точке и на множестве. Геометрический смысл производной. Уравнения касательной и нормали к графику функции в точке.
Определение производной функции в точке и на множестве. ОПРЕДЕЛЕНИЕ 1. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при (если этот предел существует и конечен), т.е. . Обозначают: .Понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке.
Геометрический смысл производной.
Геометрический смысл производной
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
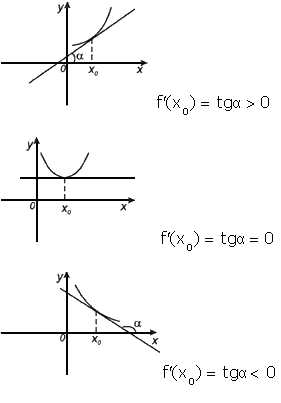
Рассмотрим график функции y = f ( x ):
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
В этом и состоит геометрический смысл производной.
Уравнения касательной и нормали к графику функции в точке.
Уравнение касательной
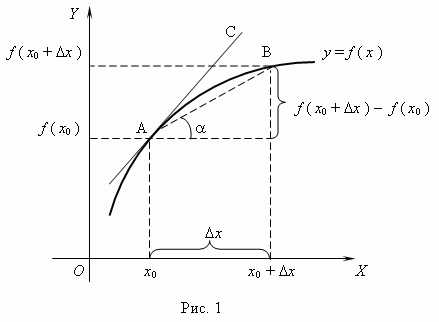
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:
y/(x)=limΔx→0ΔxΔy
Δy=f(x+Δx)−f(x).
Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=kТ.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.
Уравнение нормали
Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:y−f(x0)=−1f/(x0)(x−x0).
Примеры. Напишите уравнение касательной к графику функции y=0,5x^2–3x+1, проходящей под углом 45° к прямой y=0. Смотреть решение... Дана функция y = x^3. Составить уравнение касательной к графику этой функции в точке x0=2. Смотреть решение... Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2. Смотреть решение...fizmatinf.blogspot.com
Касательная к графику функции Уравнение касательной Геометрический
 Касательная к графику функции. Уравнение касательной
Касательная к графику функции. Уравнение касательной
 Геометрический смысл производной Производная в точке х0 равна угловому коэффициенту касательной к графику функции у = f(х) в этой точке Рассмотрим 3 случая:
Геометрический смысл производной Производная в точке х0 равна угловому коэффициенту касательной к графику функции у = f(х) в этой точке Рассмотрим 3 случая:
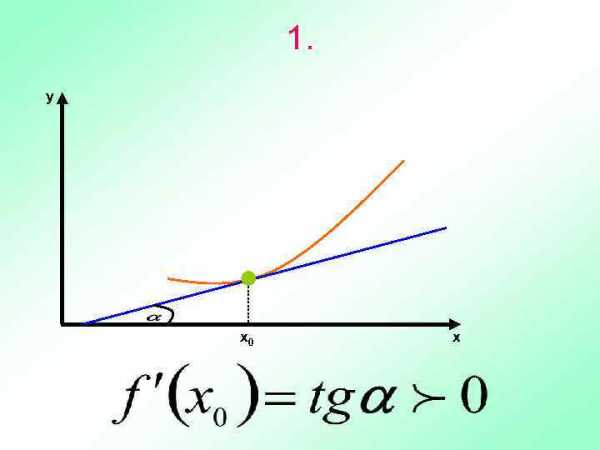 1. у х0 х
1. у х0 х
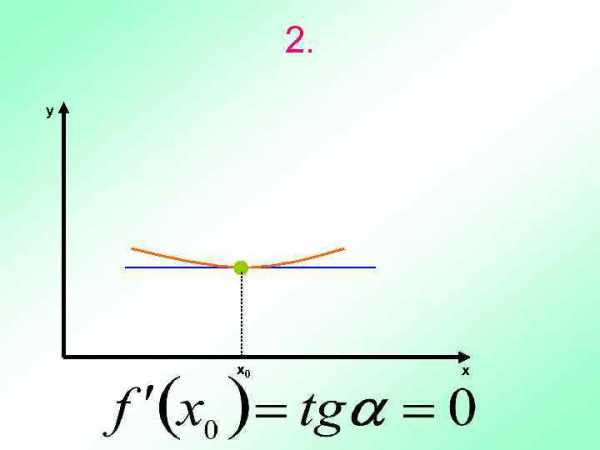 2. у х0 х
2. у х0 х
 3. у х0 х х
3. у х0 х х
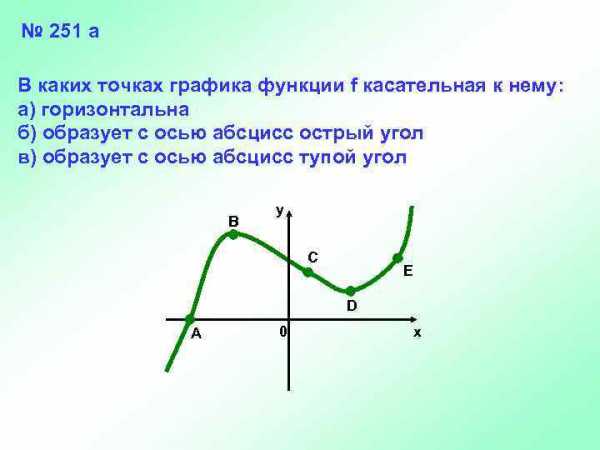 № 251 а В каких точках графика функции f касательная к нему: а) горизонтальна б) образует с осью абсцисс острый угол в) образует с осью абсцисс тупой угол B y C E D A 0 x
№ 251 а В каких точках графика функции f касательная к нему: а) горизонтальна б) образует с осью абсцисс острый угол в) образует с осью абсцисс тупой угол B y C E D A 0 x
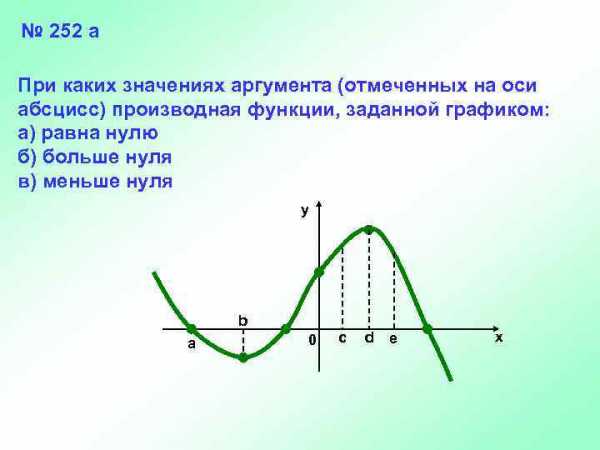 № 252 а При каких значениях аргумента (отмеченных на оси абсцисс) производная функции, заданной графиком: а) равна нулю б) больше нуля в) меньше нуля y b a 0 c d e x
№ 252 а При каких значениях аргумента (отмеченных на оси абсцисс) производная функции, заданной графиком: а) равна нулю б) больше нуля в) меньше нуля y b a 0 c d e x
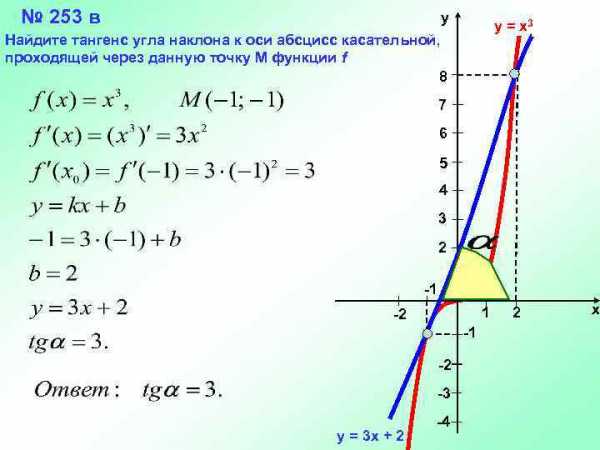 № 253 в у у = х3 Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку М функции f 8 7 6 5 4 3 2 -1 1 -2 -3 у = 3 х + 2 -4 2 х
№ 253 в у у = х3 Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку М функции f 8 7 6 5 4 3 2 -1 1 -2 -3 у = 3 х + 2 -4 2 х
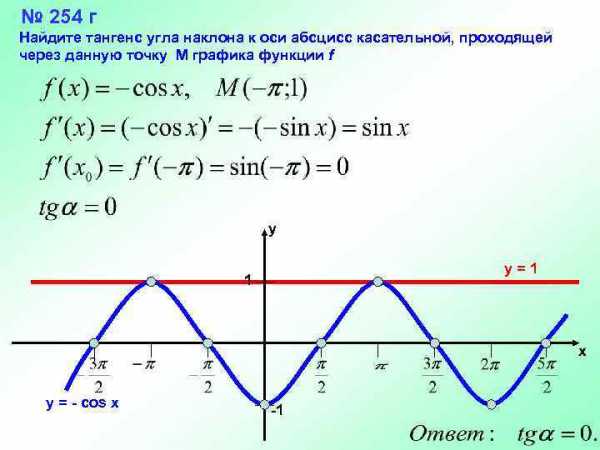 № 254 г Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку М графика функции f y y=1 1 x y = - cos x -1
№ 254 г Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку М графика функции f y y=1 1 x y = - cos x -1
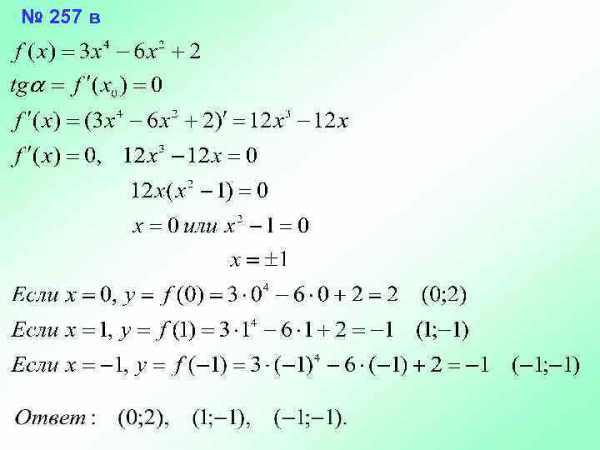 № 257 в
№ 257 в
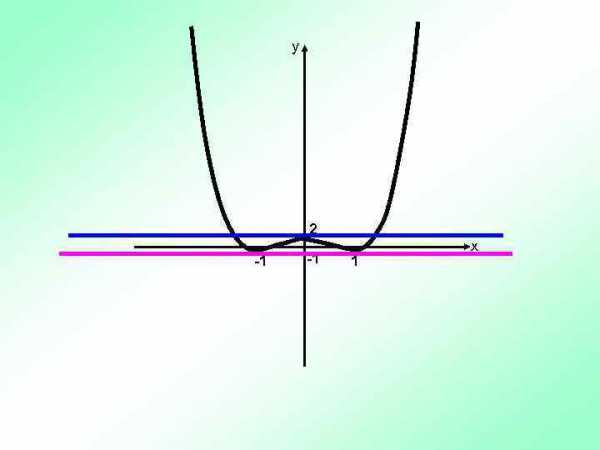 y 2 -1 -1 1 x
y 2 -1 -1 1 x
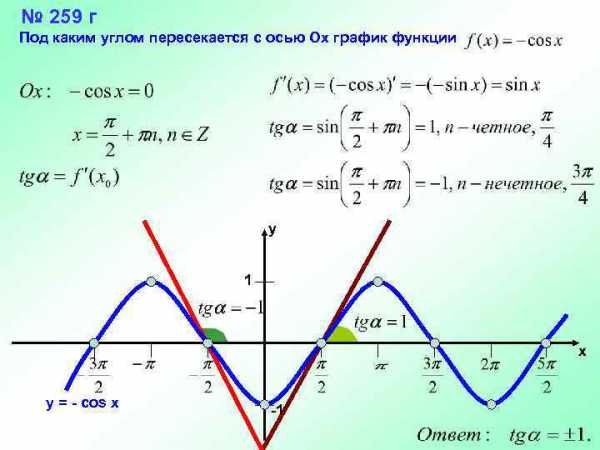 № 259 г Под каким углом пересекается с осью Ох график функции y 1 x y = - cos x -1
№ 259 г Под каким углом пересекается с осью Ох график функции y 1 x y = - cos x -1
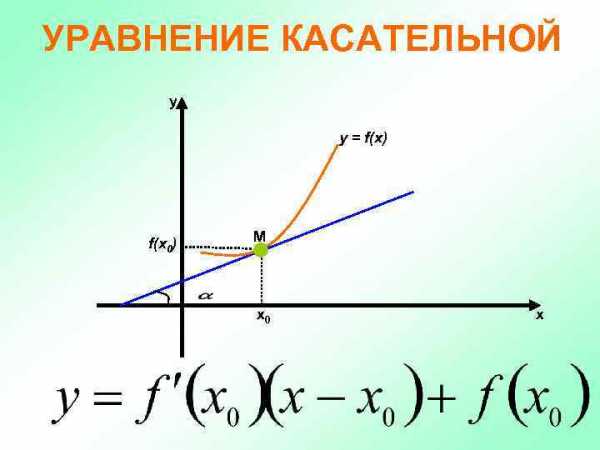 УРАВНЕНИЕ КАСАТЕЛЬНОЙ у y = f(x) f(x 0) М х0 х
УРАВНЕНИЕ КАСАТЕЛЬНОЙ у y = f(x) f(x 0) М х0 х
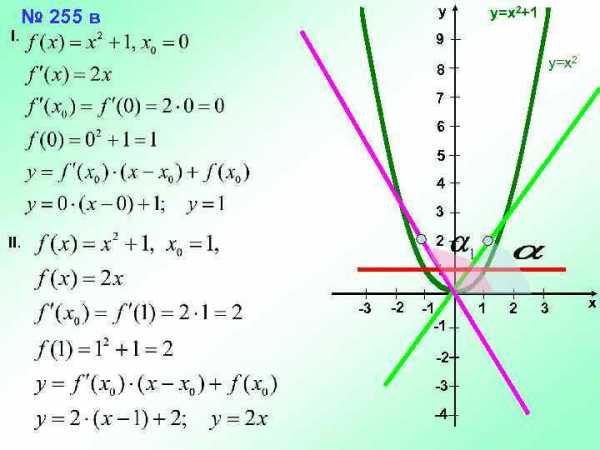 I. у № 255 в y=x 2+1 9 y=x 2 8 7 6 5 4 3 2 II. 1 -3 -2 -1 -1 -2 -3 -4 1 2 3 х
I. у № 255 в y=x 2+1 9 y=x 2 8 7 6 5 4 3 2 II. 1 -3 -2 -1 -1 -2 -3 -4 1 2 3 х
 III.
III.
present5.com
Урок по теме "Касательная. Уравнение касательной"
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (510,9 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: изучение нового материала.
Методы обучения: наглядный, частично поисковый.
Цель урока:
- Ввести понятие касательной к графику функции в точке, выяснить, в чём состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.
- Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
- Выработка коммуникативных навыков в работе, способствовать развитию самостоятельной деятельности учащихся.
Оборудование: компьютер, мультимедийный проектор, раздаточный материал.
План урока
I Организационный момент. <слайд 2, 3> Проверка готовности учащихся к уроку. Сообщение темы и девиза урока.
II Актуализация материала. (Активизировать внимание, показать недостаточность знаний о касательной, сформулировать цели и задачи урока.) <слайд 5>
Давайте обсудим, что такое касательная к графику функции? Согласны ли вы с утверждением, что «Касательная – это прямая, имеющая с данной кривой одну общую точку»? Идёт обсуждение. Высказывания детей (да и почему, нет и почему). В процессе обсуждения приходим к выводу, что данное утверждение не верно.
Примеры. <слайд 6> 1) Прямая x = 1 имеет с параболой y = x2 одну общую точку M(1; 1), однако не является касательной к параболе. Прямая же y = 2x – 1, проходящая через ту же точку, является касательной к данной параболе <рисунок 1>. 2) Аналогично, прямая x = π не является касательной к графику y = cos x, хотя имеет с ним единственную общую точку K(π; 1). С другой стороны, прямая y = - 1, проходящая через ту же точку, является касательной к графику, хотя имеет с ним бесконечно много общих точек вида
(π+2 πk; 1), где k – целое число, в каждой из которых она касается графика <рисунок 2>.
| Рисунок 1 | Рисунок 2 |
Постановка цели и задачи перед детьми на уроке: <слайд 7> выяснить, что такое касательная к графику функции в точке, как составить уравнение касательной?Что нам для этого понадобиться? Вспомнить общий вид уравнения прямой, условия параллельности прямых, определение производной, правила дифференцирования.
III Подготовительная работа к изучению нового материала. Опрос материала по карточкам: (задания выполняются на доске) 1 ученик: заполнить таблицу производных элементарных функций
2 ученик: вспомни правила дифференцирования
3 ученик: составьте уравнение прямой y = kx + 4, проходящей через точку А(3; -2). (y = -2x+4)
4 ученик: составьте уравнение прямей y = 3x + b, проходящей через точку С(4; 2). (y = 3x – 2).
С остальными фронтальная работа. <слайд 8>
- Сформулируйте определение производной.
- Какие из указанных прямых параллельны? у = 0,5х; у = - 0,5х; у = - 0,5х + 2. Почему?
Отгадай фамилию учёного <слайд 9>:
Ключ к ответам
Кем был этот учёный, с чем связаны его работы, мы узнаем на следующем уроке. Проверка ответов учащихся по карточкам. <слайд 10>
IV Изучение нового материала. Чтобы задать уравнение прямой на плоскости нам достаточно знать её угловой коэффициент и координаты одной точки.
- Начнём с углового коэффициента <слайд 11>
Рисунок 3
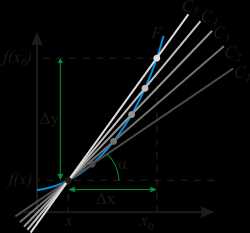
Рассмотрим график функции y = f(x) дифференцируемой в точке А(x0, f(x0)) <рисунок 3>. Выберем на нём точку M (x0 + Δх, f(x0+ Δх)) и проведем секущую AM. Вопрос: чему равен угловой коэффициент секущей? (∆f/∆x=tgβ)
Будем приближать по дуге точку M к точке A. В этом случае прямая AM будет поворачиваться вокруг точки A, приближаясь (для гладких линий) к некоторому предельному положению - прямой AT. Другими словами < TAM → 0 если длина АМ → 0. Прямую AT, обладающую таким свойством, называют касательной к графику функции y = f(x) в точке А(x0, f(x0)). <слайд 12>
Угловой коэффициент секущей AM при AM → 0 стремится к угловому коэффициенту касательной AT Δf/Δx → f '(x0). Значение производной в точке х0 примем за угловой коэффициент касательной. Говорят, что касательная есть предельное положение секущей при ∆х → 0.
Существование производной функции в точке x0 эквивалентно существованию (невертикальной) касательной в точке (x0, f(x0)) графика, при этом угловой коэффициент касательной равен f '(x0) . В этом состоит геометрический смысл производной. <слайд 13>
Определение касательной: <слайд 14> Касательная к графику дифференцируемой в точке х0функции f — это прямая, проходящая через точку (x0, f(x0)) и имеющая угловой коэффициент f '(х0). Проведем касательные к графику функции y = f(x) в точках х1, х2, х3, <рисунок 4> и отметим углы, которые они образуют с осью абсцисс. (Это угол, отсчитываемый в положительном направлении от положительного направления оси до прямой.)
Рисунок 4
Мы видим, что угол α1 острый, угол α3 тупой, а угол α2 равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла положителен, тупого — отрицателен. Поэтому f '(х1)>0, f '(х2) = 0, f '(х3) < 0. <слайд 15, 16>
- Выведем теперь уравнение касательной <слайд 17, 18> к графику функцииf в точке А(x0, f(x0)).
- Найдём угловой коэффициент k = f '(х0), получим y = f '(х0)∙x + b, f(x) = f '(х0)∙x + b
- Найдём b. b = f(x0) - f '(х0)∙x0.
- Подставим полученные значения k и b в уравнение прямой: y = f '(х0)∙x + f(x0) - f '(х0)∙x0 или y = f(x0) + f '(х0)(x - x0)
- Обобщение материала лекции. <слайд 19>
- что называется касательной к графику функции в точке? - в чём заключается геометрический смысл производной? - сформулируйте алгоритм нахождения уравнения касательной в точке?
1. Значение функции в точке касания 2. Общую производную функции 3. Значение производной в точке касания 4. Подставить найденные значения в общее уравнение касательной.
V Закрепление изученного материала.
1. Устная работа: 1) <слайд 20> В каких точках графика <рисунок 5> касательная к нему а) горизонтальна; б) образует с осью абсцисс острый угол; в) образует с осью абсцисс тупой угол? 2) <слайд 21> При каких значениях аргумента производная функции, заданной графиком <рисунок 6> а) равна 0; б) больше 0; в) меньше 0?
| Рисунок 5 | Рисунок 6 |
3) <слайд 22> На рисунке изображён график функцииf(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f '(x) в точке x0<рисунок 7>.
Рисунок 7
2. Письменная работа. № 253 (а, б), № 254 (а, б). (работа на местах, с комментарием)
3. Решение опорных задач. <слайд 23> Рассмотрим четыре типа задач. Дети читают условие задачи, предлагают алгоритм решения, один из учеников оформляет его на доске, остальные записывают в тетрадь.1. Если задана точка касания Составить уравнение касательной к графику функции f(x) = x3 – 3x – 1 в точке М с абсциссой –2. Решение:
- Вычислим значение функции: f(-2) =(-2)3 – 3(-2) – 1 = -3;
- найдём производную функции: f '(х) = 3х2 – 3;
- вычислим значение производной: f '(-2) = - 9.;
- подставим эти значения в уравнение касательной: y = 9(x + 2) – 3 = 9x + 15.
Ответ: y = 9x + 15.
2. По ординате точки касания. Составить уравнение касательной в точке графика с ординатой y0 = 1. Решение:
- Найдем абсциссу точки касания: , х0 = 1.
- Найдём производную функции: f '(х) = .
- Найдем угловой коэффициент касательной f '(х0) : f '(1)= - 1
- Теперь можно записать уравнение касательной: y = –1(x – 1) + 1 = –x + 2.
Ответ: y = –x + 2.
3. Заданного направления. Написать уравнения касательной к графику y = x3 – 2x + 7, параллельной прямой у = х. Решение. Искомая касательная параллельна прямой y = x. Значит, они имеют один и тот же угловой коэффициент k = 1, y'(х) = 3х2 – 2. Абсцисса х0 точек касания удовлетворяет уравнению 3х2 – 2 = 1, откуда х0 = ±1. Теперь можно написать уравнения касательных: y = x + 5 и y = x + 9. Ответ: y = x + 5, y = x + 9.
4. Условия касания графика и прямой. Задача. При каких b прямая y = 0,5x + b является касательной к графику функции f(х) = ? Решение. Вспомним, что угловой коэффициент касательной – это значение производной в точке касания. Угловой коэффициент данной прямой равен k = 0,5. Отсюда получаем уравнение для определения абсциссы x точки касания: f '(х) = = 0,5. Очевидно, его единственный корень –х = 1. Значение данной функции в этой точке у(1) = 1. Итак, координаты точки касания (1; 1). Теперь остается подобрать такое значение параметра b, при котором прямая проходит через эту точку, то есть координаты точки удовлетворяют уравнению прямой: 1 = 0,5 ·1 + b, откуда b = 0,5.
5. Самостоятельная работа обучающего характера. <слайд 24>
Работа в парах. Проверка: результаты решения заносятся в таблицу на доске (от каждой пары один ответ), обсуждение ответов.6. Нахождение угла пересечения графика функции и прямой. <слайд 25> Углом пересечения графика функции y = f(x) и прямой l называют угол, под которым в этой же точке прямую пересекает касательная к графику функции. № 259 (а, б), № 260 (а) – разобрать у доски.
7. Самостоятельная работа контролирующего характера. <слайд 26> (работа дифференцированная, проверяет учитель к следующему уроку)1 вариант.
- Найдите тангенс угла наклона касательной к графику функции f(x)= х3+ 27 в точке х0= -3.
- Напишите уравнение касательной к графику функции в точке с абсциссой х0= 3. Выполните рисунок.
- Выясните, является ли прямая у = 0,5х + 0,5 касательной к графику функции у = .
2 вариант.
- В каких точках касательная к графику функции f(x) = 3х2 - 12х + 7 параллельна оси х?
- Составьте уравнение касательной к графику функции f(x)= х2 - 4 в точке с абсциссой х0 = - 2. Выполните рисунок.
- Выясните, является ли прямая у = 12х – 10 касательной к графику функции у = 4х3.
3 вариант.
- В какой точке графика функции у = . касательная наклонена к оси абсцисс под углом 60°?
- Составьте уравнение касательной к графику функции , параллельно прямой у = 3х.
- Выясните, является ли прямая у = х касательной к графику функции у = sin x.
VI Подведение итогов урока. <слайд 27> 1. Ответы на вопросы - что называется касательной к графику функции в точке? - в чём заключается геометрический смысл производной? - сформулируйте алгоритм нахождения уравнения касательной в точке? 2. Вспомните цели и задачи урока, достигли ли мы данной цели? 3. В чём были трудности на уроке, какие моменты урока наиболее понравились? 4. Выставление отметок за урок. VII Комментарий домашнего задания: п. 19 (1, 2), № 253 (в), № 255 (г), № 256 (г), № 257 (г), № 259 (г). Подготовить сообщение о Лейбнице <слайд 28>.
Литература <слайд 29>
1. Алгебра и начала анализа: Учеб. для 10—11 кл. общеобразоват. учреждений / А.Н.Колмогоров, А.М.Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н.Колмогорова. - М.: Просвещение, 2004. 2. Дидактические материалы по алгебре и началам анализа для 10 класса / Б.М.Ивлев, С.М.Саакян, С.И. Шварцбурд. - М.: Просвещение, 2003. 3. Мультимедийный диск фирмы «1С». 1С: Репетитор. Математика (ч. 1) + Варианты ЕГЭ. 2006. 4. Открытый банк заданий по математике/ http://mathege.ru/
xn--i1abbnckbmcl9fb.xn--p1ai
Касательная. Задачи на касательную | Статья в журнале «Молодой ученый»
Чтобы правильно и рационально решать задачи, связанные с уравнением касательной, нужно четко понимать, что такое касательная, владеть техникой составления уравнения касательной к графику функции и представлять себе, для решения каких задач (в том числе и задач с параметрами) можно использовать метод касательной.
Опр.
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при
 (рис. 1).
(рис. 1).
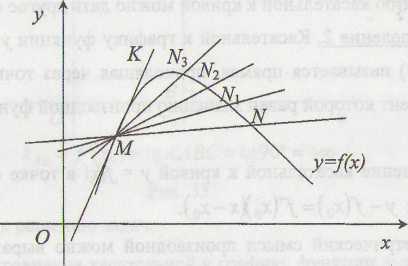
Рис. 1
Касательная к кривой может иметь с ней несколько общих точек или пересекать ее. Можно дать и другое определение касательной к кривой.
Опр. 2. Касательной к графику функции у = f(x) в точке A0(x0; f(x0)) называется прямая, проходящая через точку A0, угловой коэффициент которой равен значению производной функции у =f(x) в точке с абсциссой x0.
Уравнение касательной к кривой у = f(x) в точке с абсциссой х0имеет вид: .
Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
 ,
причем ее
угловой коэффициент
равен
,
причем ее
угловой коэффициент
равен
 .
Вывод: если в точке х0
есть производная
функции
.
Вывод: если в точке х0
есть производная
функции
 ,
то в точке с
этой абсциссой есть касательная к графику
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции
 и наоборот; если
в точке х0
нет производной
функции
и наоборот; если
в точке х0
нет производной
функции
 ,
то в точке с
этой абсциссой нет касательной к графику функции
,
то в точке с
этой абсциссой нет касательной к графику функции
 и наоборот.
и наоборот.
Укажем случаи, когда функция не имеет в точке касательной, и, следовательно, не имеет и производной. Таких случаев три: угловая точка, точка возврата, узловая точка(рис. 2 а, б, в). Особо отметим случай, когда в точке функция имеет бесконечную производную (рис. 2 г).

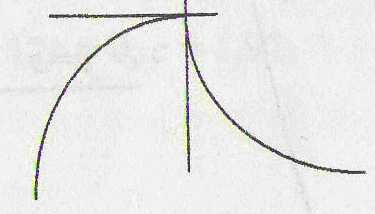


угловая точка точка возврата узловая точка
а) б) в) г)
Рис. 2
Рассмотрим решение некоторых задач.
Задачи, связанные с определением того, является ли прямая у = kx + b касательной к графику функции у = f(x). Можно указать два способа решения таких задач.
Находим общие точки графиков, т. е. решаем уравнение f(x) = kx + b, а затем для каждого из его решений вычисляем
 .
В тех случаях, когда
.
В тех случаях, когда
 = k,
имеет место касание, в других —
пересечение.
= k,
имеет место касание, в других —
пересечение.Находим корни уравнения
 = k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система
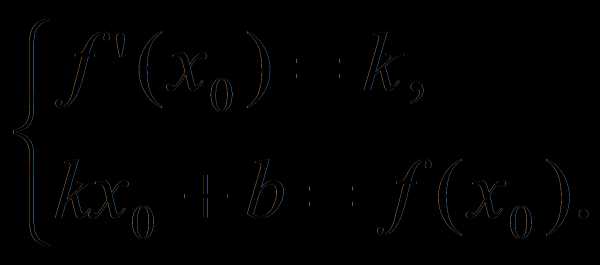
При каких значениях b прямая у = 3х +b является касательной к графику функции у =
 ?
?
Решение.
Записав условие касания
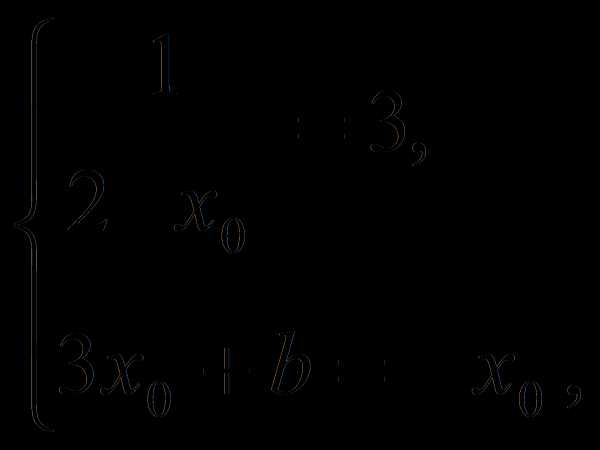 получим
получим

Ответ:
 .
.
При каких значениях а прямая у=ах+2 является касательной к графику функции

Указание.
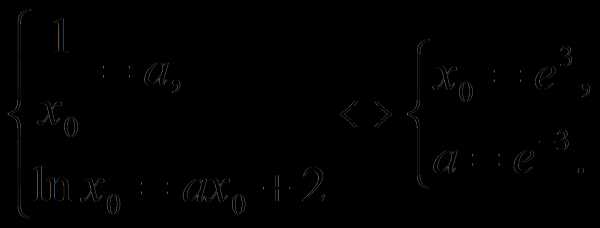
Ответ: а = e-3
При каких значениях а прямая является касательной к графику функции
Указание.
Ответ: а = 7 или а = -1.
Является ли прямая касательной к графику функции ? Если является, то найти координаты точки касания.
Решение.
Пусть
.
Из условия следует, что должны выполняться равенство
,
где
 -
возможная абсцисса точки касания. Имеем:
-
возможная абсцисса точки касания. Имеем:
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
 как раз и получится
.
Значит, точка касания имеет координаты (1;-1).
как раз и получится
.
Значит, точка касания имеет координаты (1;-1).
К графику функции проведена касательная, параллельная прямой . Найти ординату точки касания.
Решение.
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
 .
Имеем:
.
Имеем:
Таким образом, . Значит, - абсцисса точки касания. Чтобы найти ординату точки касания преобразуем выражение, задающее функцию:
Ответ: 1.
Написать уравнение всех касательных к графику функции , параллельных прямой
 .
.
Решение.
Так как касательная должна быть параллельна прямой
 ,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
 .
Отсюда
.
Отсюда
 или
или

 .
Далее составляем уравнение касательной для каждой точки.
.
Далее составляем уравнение касательной для каждой точки.
Ответ:

 ,
, .
.
Найти все значения
 ,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
 параллельны.
параллельны.
Решение.
Известно, что тангенс угла наклона касательной к графику функций
 в точке с абсциссой
в точке с абсциссой
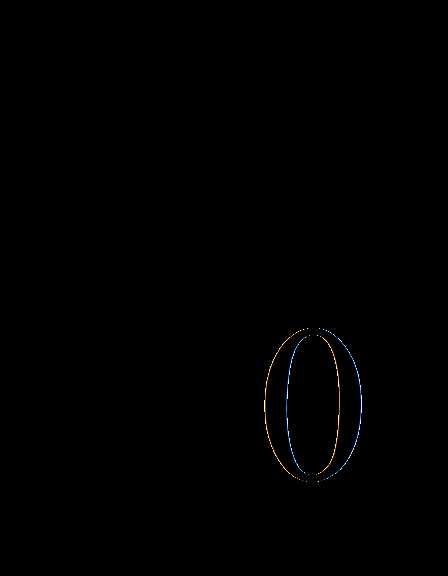 равен
равен
 .
Следовательно, все искомые значения
.
Следовательно, все искомые значения
 будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем
будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем
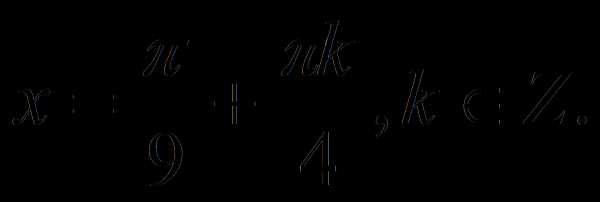
Найти расстояние между касательными к графику функции , расположенными параллельно оси
 .
.
Решение. Найдем критические точки заданной функции:
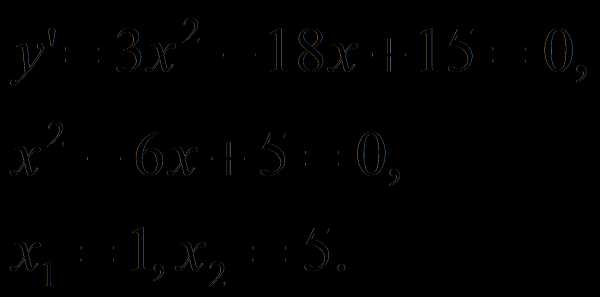
Так как,
производная в точках
 и
и
 равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
 .
Найдем значения функций в этих точках.
.
Найдем значения функций в этих точках.
Итак,
расстояние d
между касательными, параллельными оси
 ,
равно
,
равно
С составлением уравнения касательной, параллельной данной прямой, связана задача о нахождении кратчайшего расстояния между графиком некоторой функции f(x) и прямой .
Во многих
случаях удается найти касательную к графику
 ,
параллельную данной прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
,
параллельную данной прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
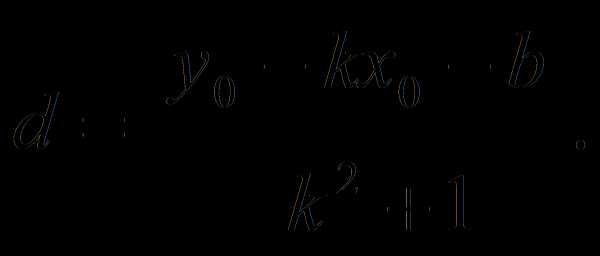
Найти кратчайшее расстояние между параболой
 и прямой
и прямой

Решение.
Убедившись, что графики не имеют общих
точек (уравнение
 не имеет решений), запишем
уравнение такой касательной к графику функции
не имеет решений), запишем
уравнение такой касательной к графику функции
 ,
которая параллельна прямой
,
которая параллельна прямой
 Уравнение касательной имеет
вид
Уравнение касательной имеет
вид
 касание происходит в точке
касание происходит в точке
 Прямая у =
Прямая у =
 х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
 .
.
Ответ:

Довольно сложной является задача составления уравнения всех касательных к графику функции у = f(x), проходящих через заданную точку М(х0; у0), вообще говоря, не лежащую на графике. Приведем алгоритм решения этой задачи.
1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:

2. Решаем
относительно t
уравнение
и для каждого его
решения t
записываем
соответствующую
касательную в виде
 .
.
Написать уравнение всех касательных к графику функции , проходящих через точку М(2; -2).
Указание. Уравнение касательной в точке с абсциссой t имеет вид . Так как эта касательная проходит через точку (2; -2), то , откуда .
Ответ: .
Найти площадь треугольника, образованного касательными, проведенными к графику функции
 через точку
через точку
 и секущей,
проходящей через точки касания.
и секущей,
проходящей через точки касания.
Указание. Уравнение дает два решения: t1 = 1, t2 = 4. Таким образом, точки K1 (1;1) и K2(4;2) являются точками касания.
Ответ: 0,25.
Говорят, что
прямая
является общей касательной графиков функции
 и
и
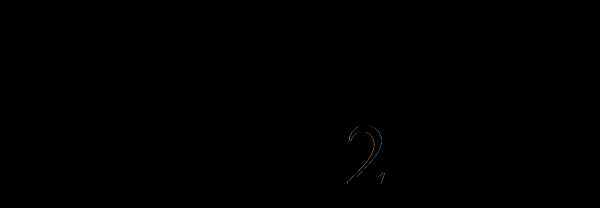 ,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
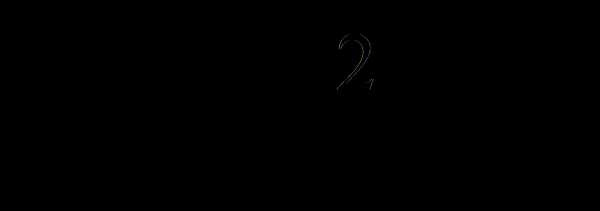 (в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
(в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
 и
и
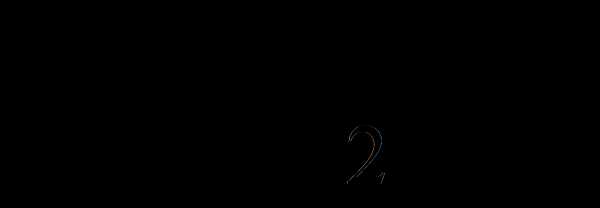 имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
Доказать, что параболы и имеют в их общей точке общую касательную. Найти уравнение этой общей касательной. Решение. Уравнение имеет единственный корень х=2, т. е. параболы имеют единственную общую точку М(2;0). Убедимся, что значения производных для обеих функций в точке х = 2 равны; действительно,
 и
и
 .
Далее составляем уравнение касательной.
.
Далее составляем уравнение касательной.
Ответ:.
В завершении рассмотрим решение еще нескольких задач на касательную с параметром.
При каких значениях параметра
 касательная
к графику функции
в точке
касательная
к графику функции
в точке
 проходит через точку (2;3)?
проходит через точку (2;3)?
Решение.
Составим уравнение касательной к графику заданной функции в точке
 :
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
:
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
 .
.
Может ли касательная к кривой
 в какой-либо ее точке составлять острый угол с положительным
направлением оси
в какой-либо ее точке составлять острый угол с положительным
направлением оси
 ?
?
Решение.
Найдем производную функции
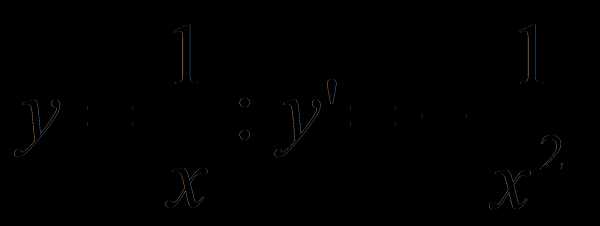 .
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не может.
Найти значение параметра
 ,
при котором касательная к графику функции
в точке
,
при котором касательная к графику функции
в точке
 проходит через точку М(1;7).
проходит через точку М(1;7).
Решение. Пусть тогда . Составим уравнение касательной:
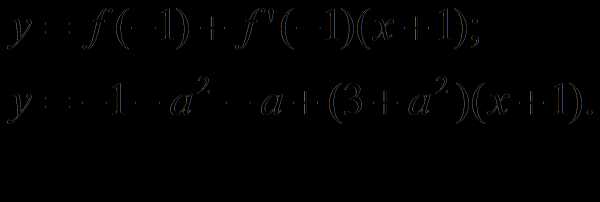
По условию эта касательная проходит через точку М(1;7), значит, , откуда получаем:
При каких значениях параметра
 прямая
является касательной к графику функции
?
прямая
является касательной к графику функции
?
Решение.
Из условия следует, что должно выполнятся равенство
где
 абсцисса
точки касания. Значит,
абсцисса
точки касания. Значит,
 и
и
 связаны между собой равенством
связаны между собой равенством
 (1). Составим уравнение касательной к графику заданной функции в
точке
(1). Составим уравнение касательной к графику заданной функции в
точке

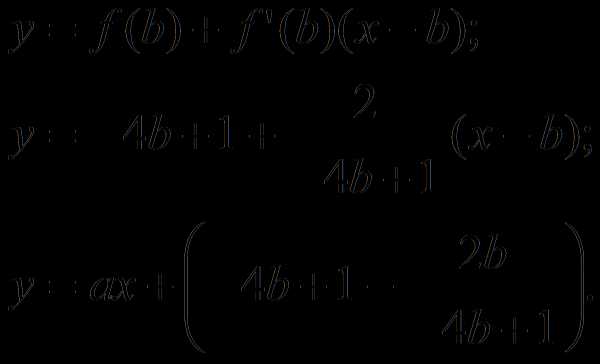
Из условия
следует, что должно выполняться равенство
.
Решив это уравнение, получим
 .
Тогда из (1) получаем, что
.
Тогда из (1) получаем, что
 .
.
При каком значении
 прямая
является касательной у графику
?
прямая
является касательной у графику
?
Решение.
Так как прямая
является касательной к графику функции
,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
откуда
 ,
следовательно,
,
следовательно,
 -
абсцисса точки касания. Найдем теперь
-
абсцисса точки касания. Найдем теперь
 из
условия равенства значений функций
и
при
из
условия равенства значений функций
и
при
 .
Имеем
,
откуда
.
Имеем
,
откуда
 .
.
При каких значениях параметра а касательные к графику функции , проведенные в точках его пересечения с осью оx, образуют между собой угол 60о?
Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
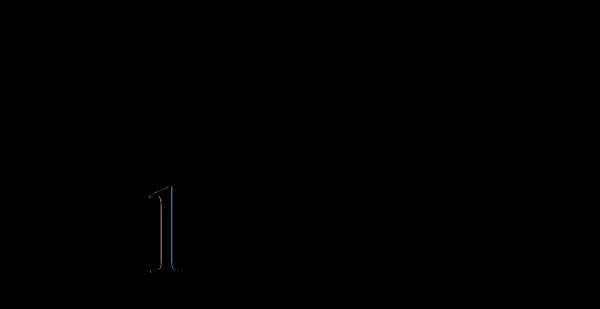 и
и
 учитываем,
что х2>0
(рис. 3)
учитываем,
что х2>0
(рис. 3)
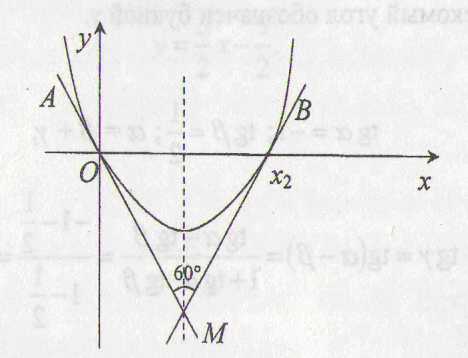
Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
 Далее имеем:
.
Таким образом, получаем, что
,
то
Далее имеем:
.
Таким образом, получаем, что
,
то
 .
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
 .
Таким образом, получаем, что
.
Таким образом, получаем, что
 ,
то есть
,
то есть

Ответ:
 .
.
Литература:
Далингер, В.А. Начала математического анализа в задачах [Текст]: учебное пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. – 312 с.
Звавич, Л.И. Алгебра и начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В. Чинкина.– М.: Дрофа, 1999. – 352 с.
moluch.ru
Касательная к графику функции — урок обобщения и систематизации знаний
Разделы: Математика
Цель занятия. Повторить владение техникой составления уравнения касательной к графику функции, систематизировать основные типы задач, при решении которых используется метод касательной.
Оборудование: компьютер; мультимедийный проектор.
Ход занятия
Повторение.
Учащиеся отвечают на вопросы (тексты на экране):
Какие из ниже приведенных определений касательной верные, а какие неверные?
1) Касательная есть предельное положение секущей при
2) Касательная к графику дифференцируемой в точке х0 функции f – это прямая, проходящая через точку (х0;f(x0)) и имеющая угловой коэффициент f \(х0).
3)Касательной к графику функции называется прямая, имеющая с данной кривой единственную общую точку.
Если функция непрерывна в точке, но не имеет в этой точке производной, то какой вывод можно сделать относительно касательной к графику функции в этой точке?
Учащиеся отвечают, что, вообще говоря, неверным является третье определение. В этом случае достаточно привести один пример.
Прямая х=2 имеет с параболой у=(х-1)2 одну общую точку (2;1), но касательной не является. Прямая у=2х-3, проходящая через эту точку, является касательной к графику данной функции.
Покажем это. Мы знаем, что если существует производная функции у=f(x) в точке х0, то существует и касательная к графику этой функции. Уравнение касательной имеет вид:
у= f(x0)+f \(x0)(х-х0)
у \(х)=2х-2, у \(х0)=у \(2)=2, у(х0)=у(2)=1. Уравнение касательной
у=1+2(х-2)=2х-3, у=2х-3.
Ответ на второй вопрос дан в п.19,с.129.Алгебра и начала математического анализа.10-А45 11 классы: учебник для общеобразовательных учреждений с приложением на электронном носителе / [ А.Н.Колмогоров, А.М.Абрамов, Ю.Н.Дудницын и др.]; под редакцией А.Н. Колмогорова-18-е изд.-М.: Просвещение, 2009 , а именно, если же f \(x0) не существует( как у функции , в точке (0;0), либо вертикальна ( как у графика функции в точке (0;0))
Учитель. На сегодняшнем занятии мы с вами рассмотрим четыре основных типа задач на касательную:
- составить уравнение касательной к графику функции в точке на этом графике;
- составить уравнение касательной к графику функции, параллельной данной прямой;
- составить уравнения касательных к графику данной функции, проходящих через заданную точку;
- составить уравнения общих касательных для графиков двух функций.
Первые два типа задач вам хорошо известны; решения этих задач рассмотрим на экране.
Задача 1. Составить уравнение касательной к графику функции у=х3-2х+3 в точке А(-1;4), лежащей на графике.
Решение. Уравнение касательной к графику функции f в точке А(х0;f(х0)) имеет вид:
y=f(x0)+f \(x0)(x-x0)
В нашей задаче х0= -1,f(x0)=f(-1)=4, f \(x0)=f \(-1)=.
Подставляя эти числа в уравнение касательной, получим уравнение у=4+(х+1), т.е. у=х+5
Ответ: у=х+5
Задача 2. Написать уравнение всех касательных к графику функции
у=х3-2х+7, параллельных прямой у=х.
Решение. Параллельные прямые имеют равные угловые коэффициенты, поэтому у \(x0)=1, где у \(х0) – значение производной функции у=х3-2х+7,х0- абсцисса точки касания.
Находим у\(х)= 3х2-2, , х0=1 или х0= -1
Для каждой из этих точек составляем уравнение касательной.
y=f(x0)+f \(x0)(x-x0)
x0 =1,f(x0)=f(1)=6;f \(x0)=f \(1)=1; y=6+(x-1)=x+5; y=x+5
x0= -1, f(x0)=f(-1)=8;f \(x0)=f \(-1)=1;у=8+(х+1)=х+9; у=х+9
Ответ: у=х+5,у=х+9
Следующие задачи решаются у доски с записью решений в тетрадях.
Задача 3. Написать уравнение всех касательных к графику функции у=х2—4х+3, проходящих через точку А(3;-2).
Учитель. При решении таких задач составляется уравнение касательной, а затем это уравнение решается относительно х0и для каждого х0 находится соответствующее уравнение касательной.
Решение. Убедимся, что точка А(4;-1) не лежит на графике данной функции.
Действительно, 42-4+3.
Находим f(x0)=-4
Уравнение касательной у=(х-х0)
Так как касательная проходит через точку А(4;-1), то ее координаты удовлетворяют уравнению касательной.
Составим уравнение касательной для каждого значения х0.
При х0=6 имеем f(x0)=15, , у=15+8(х-6)=8х-33, у=8х-33- уравнение первой касательной.
При х0=2 имеем f(x0)=-1, f(х0)=-1,f\(х0)=0, у= -1- уравнение второй касательной. Это уравнение касательной можно составить, учитывая, что вторая координата вершины параболы имеет значение -1.
Ответ: у=8х-33,у= -1
Задача 4. Найдите уравнение всех общих касательных к графикам функций у=3х2-5х-2 и у=2х2-х-6.
Решение. Пусть х=t – абсцисса точки касания всех касательных к графику функции у=3х2-5х-2 .
Уравнение всех касательных к графику этой функции имеет вид:
у=3t2-5t-2+(6t-5)(x-t)
Пусть и – абсцисса всех касательных к графику функции у=2х2-х-6.
Получим уравнение всех касательных:
у=2и2-и-6+(4и-1)(х-и)
Полученные два уравнения задают одну и туже прямую. Следовательно, надо решить систему
Учитывая равенство 6t-5=4u-1, второе уравнение системы запишем в виде
3t2-5t-2-(6t-5)t=2u2-u-6-(4u-1)u
или после упрощения 3t2-2u2-u=0
Из первого уравнения системы .
Подставляя в последнее уравнение, получим (t-2)2=0, t=2, тогда u=2.
Получили уравнение единственной касательной у=7х-14
Ответ: у=7х-14
Учитель. Рассмотрим еще две задачи на касательную. Прежде всего, представляют интерес задачи, где требуется определить является ли прямая у= кх+b касательной к графику функции у=f(x) и как уравнение касательной используется при нахождении площадей фигур.
Задача 5. При каких значениях параметра а прямая у= ах+ касается графика функции .
Решение. Если существует хотя бы одно значение х0, для которого имеет решение система , где х0 - абсциссы общих точек графиков функций у=кх+b и у=f(x), то прямая у=кх+b является касательной к графику у=f(x).
Находим .
Решим систему
Из первого уравнения системы
Подставляя во второе уравнение системы, получим
Откуда
Ответ: а=
Задача 6. Найти площадь треугольника, образованного касательными, проведенными к графику функции f(x)=3x-x2, проходящими через точки А(1;3) и В(1;2).
Решение. Запишем уравнение касательной к графику функции f(x) в точке с абсциссой х0
y=f(x0)+f \(x0)(x-x0)
Точка А(1;3) находится вне параболы, так .
Находим f \(x0)=3-2x, f \(x0)=3-2x0, f(x0)=3x0 – x02.
Тогда уравнение касательной примет вид
или у =
Касательная проходит через точку А(1;3), поэтому
Получили, что через точку А(1;3) проходит две касательные к параболе f(x)=3x-x2, а именно у=3х и у = - х+4.
Точка В(1;2)лежит на параболе, так как 2=, и уравнение касательной имеет вид у=2+(х-1)=х+1
На рис.1 изображена парабола с вершиной ,точками пересечения с осью абсцисс О(0;0),Е(3;0) и касательными, которые образуют треугольник АСD, площадь которого требуется найти.
Рис.1
Найдем координаты точек пересечения касательной у=х+1 с касательными у=3х и у = -х+4. Для этого решим совокупность двух систем
Получили
Теперь найдем длины сторон треугольника ACD по формуле расстояния между двумя точками
,
Для нахождения площади треугольника воспользуемся формулой Герона
Вычислим отдельно:
Далее имеем:
Ответ: 0,5
Задание на дом.
1. Составьте уравнение касательной к графику функции у=х3-2х+3 в точке А(-1;4).
2. Составить уравнения касательных, проведенных к графику функции у = -2х2-х-3 в точках пересечения графика с прямой у = -х-11. Сделать чертеж.
3. Составьте уравнения всех общих касательных к графикам функций
у = х2-х+1 и у=2х2-х+0,5
Для более подготовленных учащихся вместо задачи №1 можно предложить задачу: Вычислить площадь треугольника, образованного тремя касательными, проведенными к графикам функции в точках с абсциссами х1= -2, х2 =2, х3=6
Литература
1. Звавич Л.И. и др.Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы \ .И.Звавич, Л.Я.Шляпочник,М.В. Чинкина, Дрофа, 1999.\
2.Звавич Л.И. и др. Алгебра и начала анализа. Решение задач письменного экзамена.11кл\Л.И.Звавич, Л.Я.Шляпочник, И.Кулагина.-М.: Дрофа,2000\
3.Кравцев СВ. и др Методы решения задач по алгебре: от простых до самых сложных \С.В. Крацев и др..-М.:Издательство: “Экзамен”, 2005/
4.Нараленков М.И. Вступительные экзамены по математике. Алгебра: как решать задачи: Учебно- практическое пособие \М.И. Нараленков.-М.: Издательство “Экзамен”,2003\
5.Математика. Подготовка к ЕГЭ-2009. Вступительные испытания. Под редакцией Ф.Ф.Лысенко.- Ростов – на – Дону: Легион,2008 (“Готовимся к ЕГЭ”)
6.СадовничийЮ.В. Алгебра. Конкурсные задачи с решениями: учебное пособие \Ю.В.Садовничий.-М.:Издательство “Экзамен”,2007\
xn--i1abbnckbmcl9fb.xn--p1ai
Касательная - это... Что такое Касательная?
График функции (чёрная кривая) и касательная прямая (красная прямая)
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Определение
Замечание
Прямо из определения следует, что график касательной прямой проходит через точку (x0,f(x0)). Угол α между касательной к кривой и осью Ох удовлетворяет уравнению
где обозначает тангенс, а — коэффициент наклона касательной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Касательная как предельное положение секущей
Пусть и Тогда прямая линия, проходящая через точки (x0,f(x0)) и (x1,f(x1)) задаётся уравнением
Эта прямая проходит через точку (x0,f(x0)) для любого и её угол наклона α(x1) удовлетворяет уравнению
В силу существования производной функции f в точке x0, переходя к пределу при получаем, что существует предел
а в силу непрерывности арктангенса и предельный угол
Прямая, проходящая через точку (x0,f(x0)) и имеющая предельный угол наклона, удовлетворяющий задаётся уравнением касательной:
y = f(x0) + f'(x0)(x − x0).Касательная к окружности
Отрезки касательных
Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.
Свойства
- Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с радиусом, является тангенсом угла между этим радиусом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».
Вариации и обобщения
Односторонние полукасательные
- Если существует левая производная то ле́вой полукаса́тельной к графику функции f в точке x0 называется луч
- Если существует бесконечная правая производная то правой полукасательной к графику функции f в точке x0 называется луч
- Если существует бесконечная левая производная то правой полукасательной к графику функции f в точке x0 называется луч
См. также
Wikimedia Foundation. 2010.
dic.academic.ru