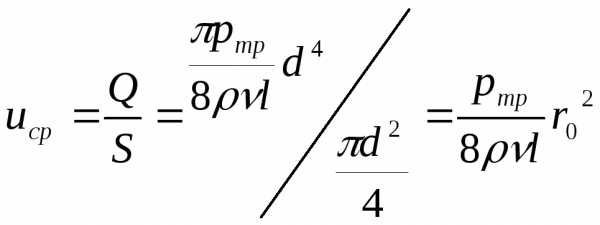Ламинарный Режим движения жидкости. Ламинарный режим
Ламинарный Режим движения жидкости
Ламинарным течением жидкости называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления.
Закон распределения скоростей по сечению круглой трубы при ламинарном режиме движения, установленный английским физиком Дж. Стоксом, имеет вид
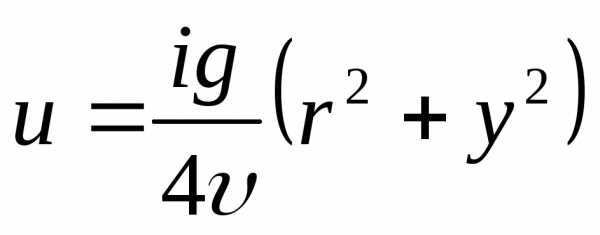 ,
,
где 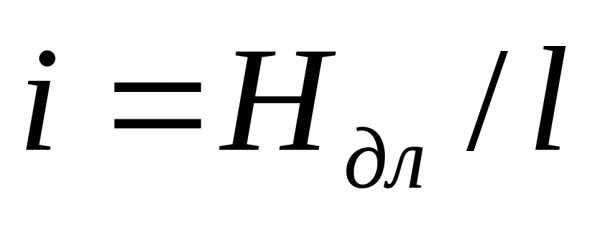 ,
,
 - потери напора по длине.
- потери напора по длине.
При 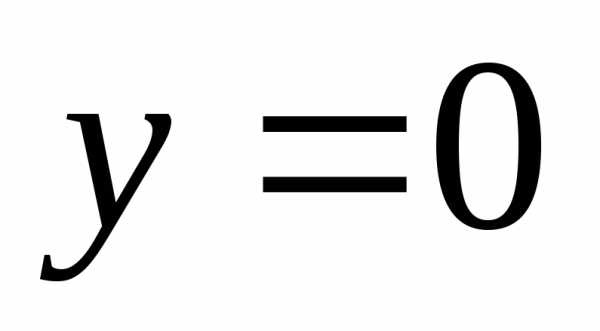 , т.е. на оси трубы
, т.е. на оси трубы ,
,
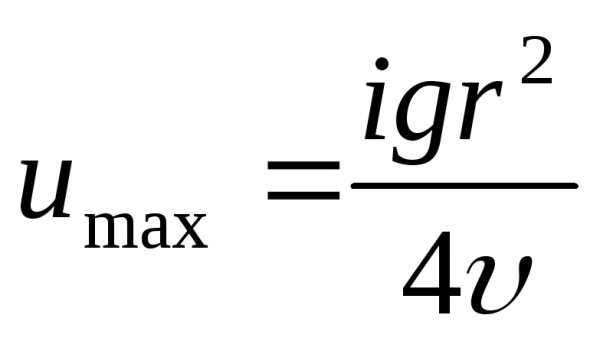 .
.
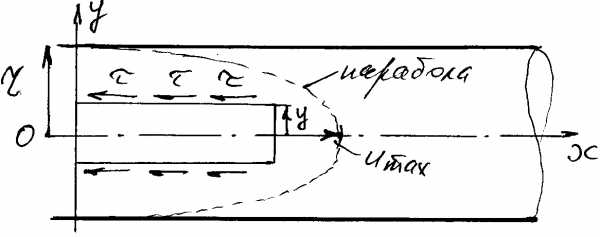
При ламинарном движении эпюра скоростей по поперечному сечению трубы будет иметь форму квадратичной параболы.
Турбулентный Режим движения жидкости
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений.
В результате наличия вихрей и интенсивного перемешивания частиц жидкости в любой точке турбулентного потока в данный момент времени имеет место своя по значению и направлению мгновенная местная скорость u, а траектория частиц, проходящих через эту точку, имеет различный вид (занимают разное положение в пространстве и имеют различную форму). Такое колебание во времени мгновенной местной скорости называется пульсацией скорости. То же происходит и с давлением. Таким образом, турбулентное движение является неустановившимся.
Усредненная местная скорость ū – фиктивной средней скорости в данной точке потока на достаточно длительный промежуток времени, которая несмотря на значительные колебания мгновенных скоростей, остается практически постоянной по значению и параллельной оси потоков
| | |
П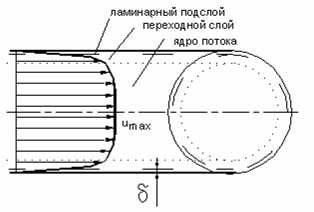
Ламинарный подслой, расположенный непосредственно у стенок трубы, имеет весьма малую толщину δ, которая может быть определена по формуле
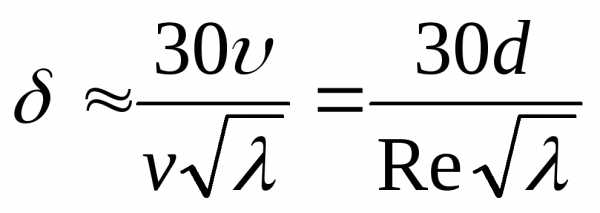 .
.
В переходном слое ламинарное течение уже нарушается поперечным перемещением частиц, причем чем дальше расположена точка от стенки трубы, тем выше интенсивность перемешивания частиц. Толщина этого слоя также невелика, но четкую его границу установить трудно.
Основную часть живого сечения потока занимает ядро потока, в котором наблюдается интенсивное перемешивание частиц, поэтому именно оно характеризует турбулентное движение потока в целом.
ПОНЯТИЕ О ГИДРАВЛИЧЕСКИ ГЛАДКИХ И ШЕРОХОВАТЫХ ТРУБАХ
Поверхность стенок труб, каналов, лотков имеют ту или иную шероховатость. Обозначим высоту выступов шероховатости буквой Δ. Величину Δ называютабсолютной шероховатостью, а ее отношение к диаметру трубы (Δ/d) - относительной шероховатостью; величина обратная относительной шероховатости, носит название относительной гладкости (d/Δ).
В зависимости от соотношения толщены ламинарного подслоя δ и высоты выступов шероховатости Δ различают гидравлически гладкие и шероховатые трубы. Если ламинарный подслой полностью покрывает все выступы на стенках трубы, т.е. δ>Δ, трубы считаются гидравлически гладкими. При δ<Δ трубы считаются гидравлически шероховатыми. Так как значение δ зависит от Re, то одна и та же труба может быть в одних и тех же условиях гидравлически гладкой (при малых Re), а в других – шероховатой (при больших Re).
Лекция №9
ГИДРАВЛИЧЕСКИЕ ПОТЕРИ
ОБЩИЕ СВЕДЕНИЯ.
При движении потока реальной жидкости происходят потери напора, так как часть удельной энергии потока затрачивается на преодоление различных гидравлических сопротивлений. Количественное определение потерь напора hп является одной из важнейших задач гидродинамики, без решения которой не возможно практическое использование уравнения Бернулли:
,
где α – коэффициент кинетической энергии, равный для турбулентного потока 1,13, а для ламинарного - 2; v -средняя скорость потока; h - уменьшение удельной механической энергии потока на участке между сечениями 1 и 2, проходящее в результате сил внутреннего трения.
Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.
Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:
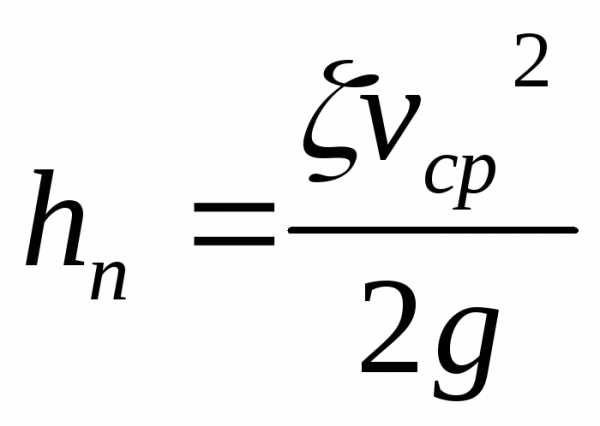 ,
,
или в единицах давления
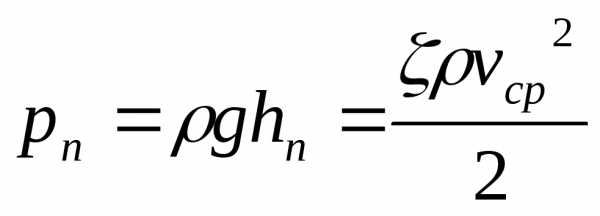 .
.
Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ζ называемый коэффициентом потерь, или коэффициентом сопротивления, значение которого для данного русла в первом грубом приближении постоянно.
Коэффициент потерь ζ, таким образом, есть отношение потерянного напора к скоростному напору.
Гидравлические потери обычно разделяют на местные потери и потери на трение по длине.
Местные потериэнергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размера русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям.
Местные потери напора определяются по формуле Вейсбаха следующим образом:
 ,
,
или в единицах давления

где v - средняя по сечению скорость в трубе, в которой установлено данное местное сопротивление.
Если же диаметр трубы и, следовательно, скорость в ней изменяются по длине, то за расчетную скорость удобнее принимать бόльшую из скоростей, т.е. ту, которая соответствует меньшему диаметру трубы.
Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления ζ, которое во многих случаях приближенно можно считать постоянным для данной формы местного сопротивления.
Потери на трение по длине, - это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним в жидкости, а потому имеют место не только в шероховатых, но и гладких трубах.
Потери напора на трение можно выразить по общей формуле для гидравлических потерь, т.е.
 ,
,
однако удобнее коэффициент ζ связать с относительной длинной трубы l/d.
 .
.
Тогда потери напора на трение определяются по формуле Вейсбаха-Дарси:
 ,
,
или в единицах давления
 .
.
Безразмерный коэффициент λ называют коэффициентом потерь на трение по длине, или коэффициентом Дарси. Его можно рассматривать как коэффициент пропорциональности между потерей напора на трение, и произведением относительной длины трубы на скоростной напор.
Нетрудно выяснить физический смысл коэффициентаλ, если рассмотреть условие равномерного движения в трубе цилиндрического объема длиной l и диаметром d, т.е. равенство нулю суммы сил, действующих на объем: сил давления и сил трения. Это равенство имеет вид
,
где  - напряжение трения на стенке трубы.
- напряжение трения на стенке трубы.
Если учесть 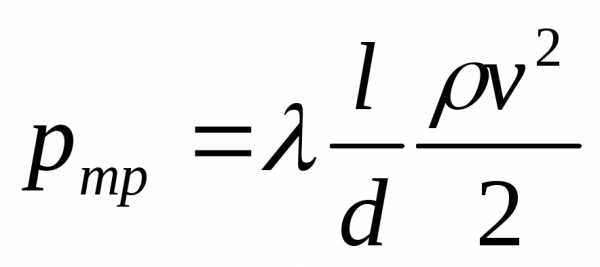 , томожно получить
, томожно получить
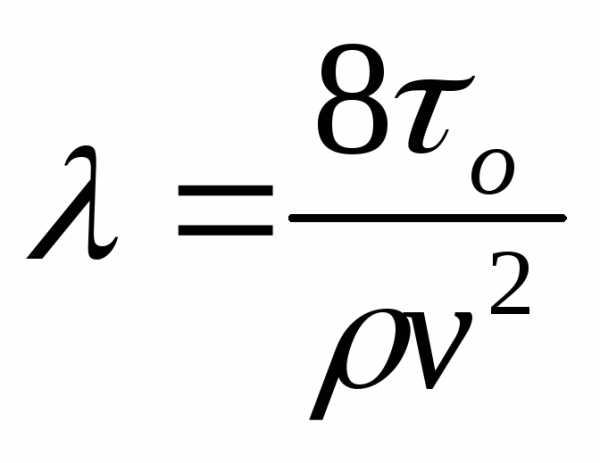 ,
,
т.е. коэффициент λ есть величина, пропорциональная отношению напряжения трения на стенке трубы к динамическому давлению, определенному по средней скорости.
Ввиду постоянства объемного расхода несжимаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются постоянными, несмотря на наличие гидравлических сопротивлений и потерь напора. Потери напора в этом случае определяются разностью показаний двух пьезометров.
Лекция №10
studfiles.net
14 Ламинарный режим движения
14-6
Рассмотрим распределение скоростей по сечению и потери напора по длине трубы при установившемся ламинарном движении.
Движение равномерное, следовательно эпюра скоростей постоянная по длине трубы. Дополнительное условие: движение изотермическое, то есть температура не меняется, а значит плотность и вязкость тоже.
Режим ламинарный (определение было ранее: слоистое движение без перемешивания, Re≤2320).
|
|
Выделим цилиндрический объем движущейся жидкости радиусом  и применим к нему основное уравнение равномерного движения жидкости
и применим к нему основное уравнение равномерного движения жидкости
здесь – касательное напряжение
– касательное напряжение
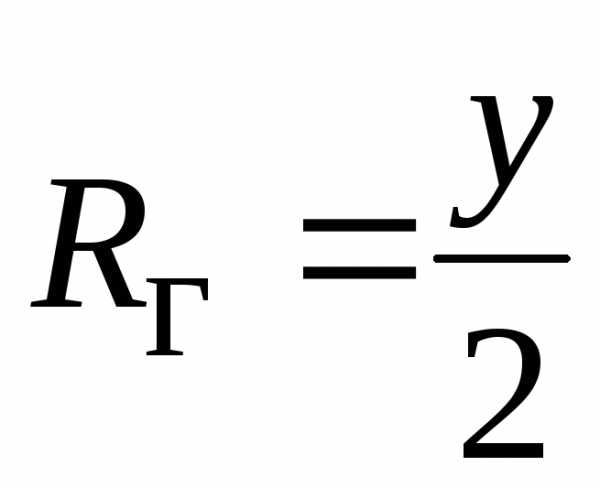 – гидравлический радиус ,
– гидравлический радиус ,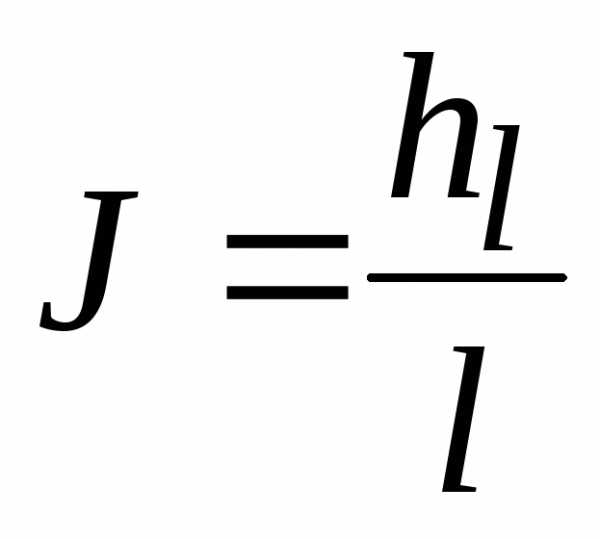 – гидравлический уклон
– гидравлический уклон
По закону Ньютона  , минус потому, что производная отрицательна, т.е. вдоль оси
, минус потому, что производная отрицательна, т.е. вдоль оси скорость падает, а всегда
скорость падает, а всегда >0.
>0.
 => ( ;
=> ( ; ) =>
) => 
интегрируем:

Постоянную интегрирования  находим из условия, что на стенке при
находим из условия, что на стенке при
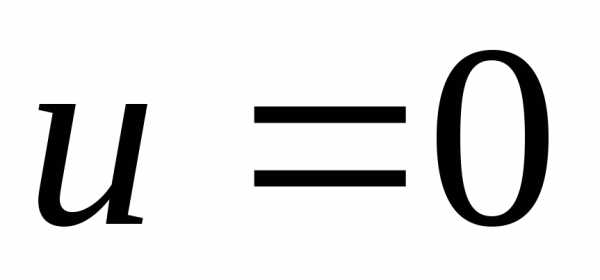 (гипотеза прилипания):
(гипотеза прилипания):
| Окончательно |
| распределение скоростей по сечению в ламинарном режиме |
Это парабола, максимум при 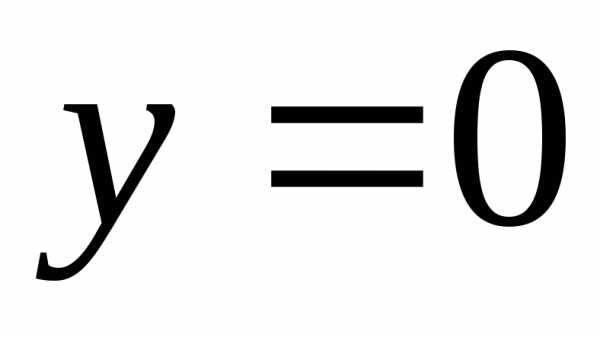 максимальная скорость
максимальная скорость
Найдем расход жидкости
Интегрируем по всему сечению по 
Учитывая, что  =>
=> 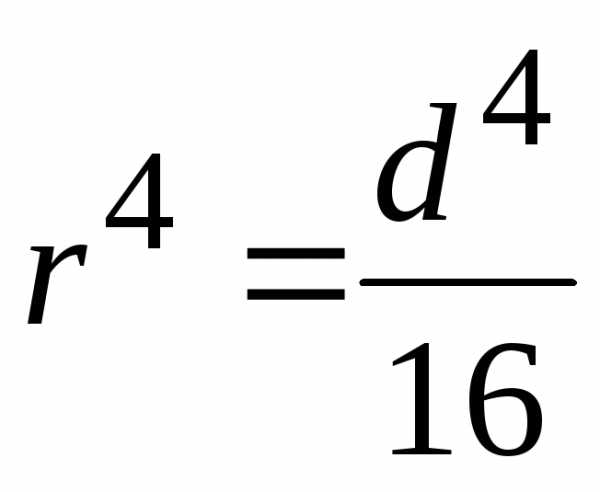
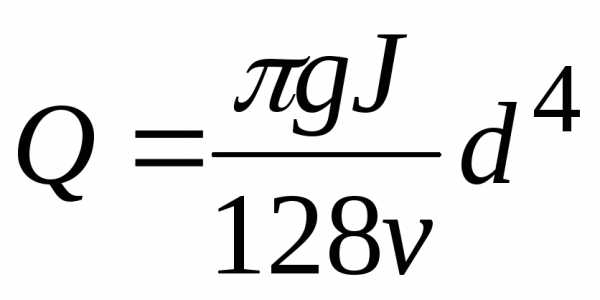
Заметим: расход в ламинарном режиме при заданном гидравлическом уклоне  пропорционален четвертой степени диаметра.
пропорционален четвертой степени диаметра.
Найдем среднюю скорость
Средняя скорость (по определению отношение объемного расхода к площади) 
Учитывая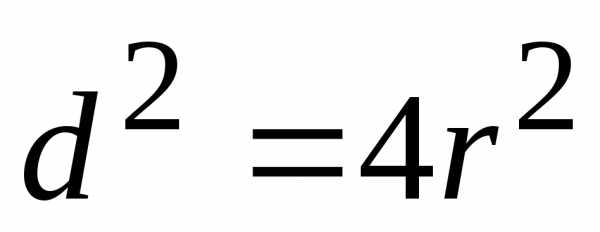
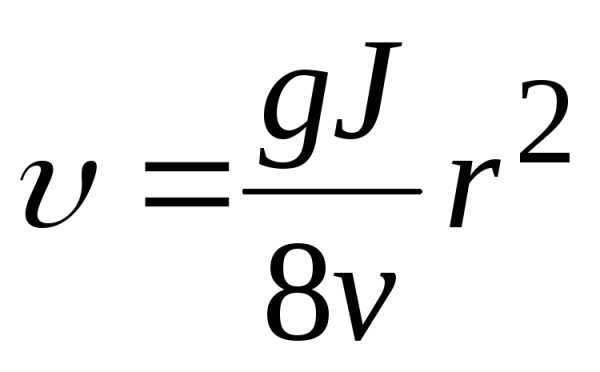
Средняя скорость ровно в два раза меньше максимальной, 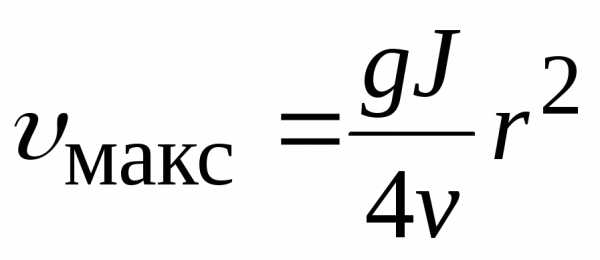 ,
, .
.
Коэффициент Кориолиса для ламинарного режима движения
 (см. примечание1)
(см. примечание1)
Найдем потери напора по длине трубы
Из выражения для средней скорости выразим гидравлический уклон
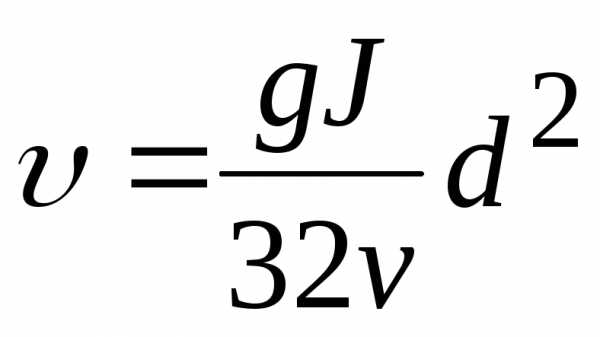 =>
=> 
С другой стороны гидравлический уклон (по определению) 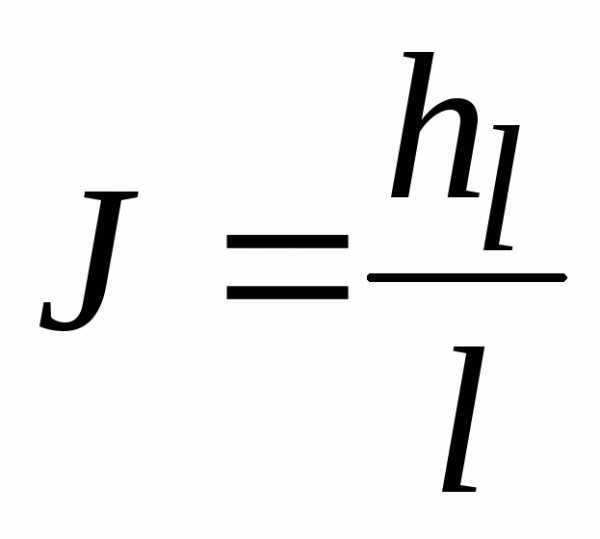 , следовательно:
, следовательно:
|
| формула Пуазейля |
Из формулы видно: потери напора по длине трубы пропорциональны средней скорости потока в первой степени.
Для определения потерь напора по длине трубы обычно используется формула Дарси
 , где
, где – коэффициент сопротивления Дарси
– коэффициент сопротивления Дарси
Чтобы найти коэффициент Дарси используем только что полученную формулу Пуазейля
используем только что полученную формулу Пуазейля
 Отсюда
Отсюда . Заметим, что
. Заметим, что
Получим : в ламинарном режиме коэффициент Дарси 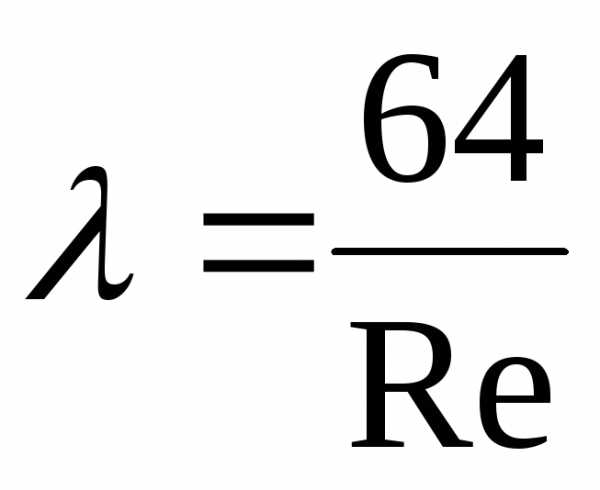
Замечание. Формула Дарси справедлива в ламинарном режиме, однако это не означает, что потери напора в этом случае пропорциональны квадрату скорости. Сам коэффициент Дарси пропорционален скорости в степени минус один (скорость входит в число Re). Следовательно, как и утверждалось ранее, потери напора по длине трубы при ламинарном режиме движения пропорциональны средней скорости потока в первой степени.
|
|
Начальный участок течения – участок от начала трубы, на котором формируется параболический профиль скоростей. За пределами этого участка имеем стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы ни была длинна труба, при условии сохранения ее прямолинейности и постоянства сечения.
Длина начального участка– расстояние от входа в трубопровод до сечения, в котором скорость распределена по параболическому закону с точностью 1%.
Потери на начальном участке больше примерно на 9%
Происходит стабилизация профиля скоростей, а производные  выше, чем в основном участке трубы. В практических расчетах увеличением потерь на начальном участке обычно пренебрегают, однако учитывают потери на вход из бака в трубу
выше, чем в основном участке трубы. В практических расчетах увеличением потерь на начальном участке обычно пренебрегают, однако учитывают потери на вход из бака в трубу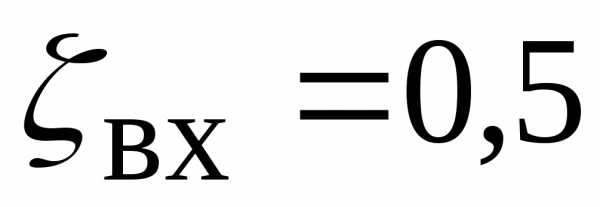 .
.
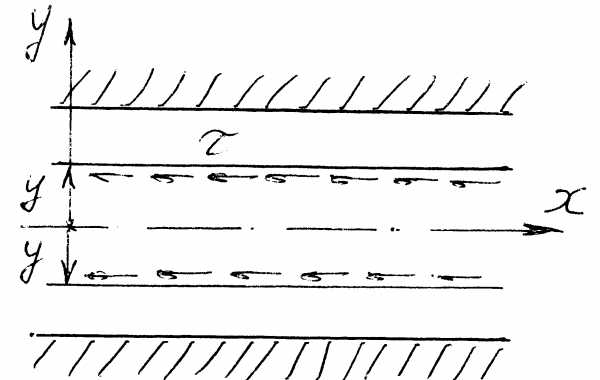
Ламинарное течение в узких щелях (зазорах)
Рассмотрим плоский зазор между неподвижными пластинами.
Толщина (величина) зазора  , длина зазора по направлению движения жидкости
, длина зазора по направлению движения жидкости , ширина зазора
, ширина зазора . Жидкость движется через зазор под действием перепада давления. Полагаем, что течение установившееся и изотермическое (температура жидкости не меняется) и вязкость жидкости постоянна.
. Жидкость движется через зазор под действием перепада давления. Полагаем, что течение установившееся и изотермическое (температура жидкости не меняется) и вязкость жидкости постоянна.
|
| Рассмотрим малый слой жидкости высотой На этот слой действуют тормозящие касательное напряжение, по закону Ньютона: |
 , здесь
, здесь – динамическая вязкость жидкости,
– динамическая вязкость жидкости, – градиент скорости слоистого движения в направлении оси
– градиент скорости слоистого движения в направлении оси , величина отрицательная, т.к. скорость местная скорость потока
, величина отрицательная, т.к. скорость местная скорость потока уменьшается при увеличении
уменьшается при увеличении , поэтому в формуле знак минус.
, поэтому в формуле знак минус.
Запишем основное уравнение равномерного движения для выделенного фрагмента:
, где – касательное напряжение;
– касательное напряжение;
 – гидравлический радиус, по определению
– гидравлический радиус, по определению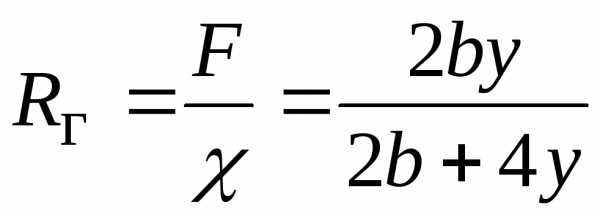 , т.к.
, т.к. , то
, то ;
;
 – гидравлический уклон, по определению
– гидравлический уклон, по определению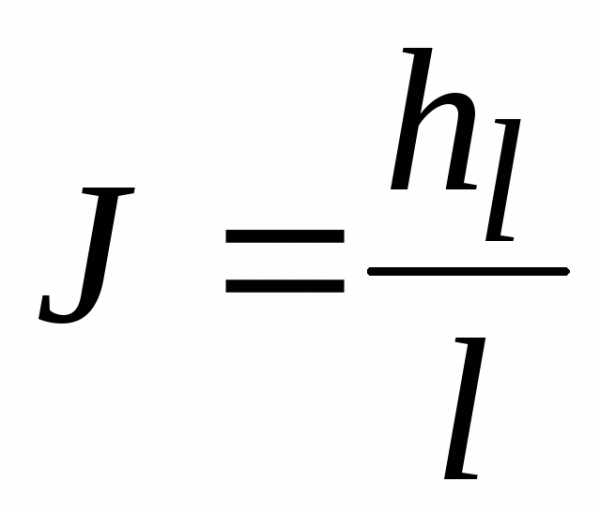 .
.
Приравняем выражения для  :
: , откуда
, откуда
Интегрируем 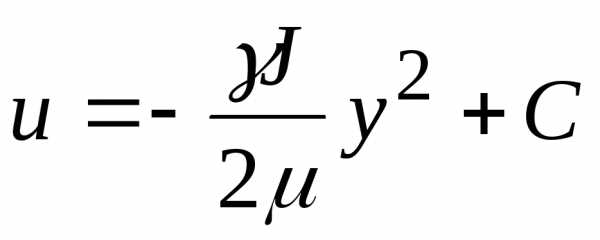
Для нахождения постоянной интегрирования воспользуемся граничным условием, вытекающим из гипотезы прилипания : при  имеем
имеем , откуда
, откуда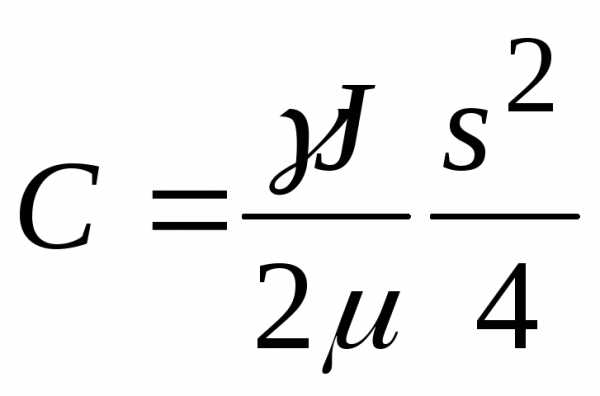
Скорость при движении в щели
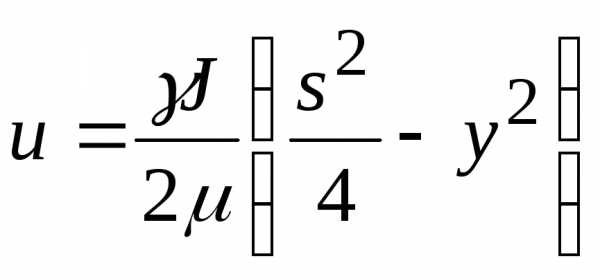
Это уравнение параболы, скорость максимальна при 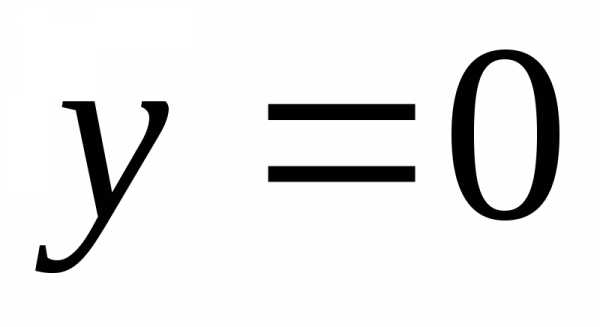 :
: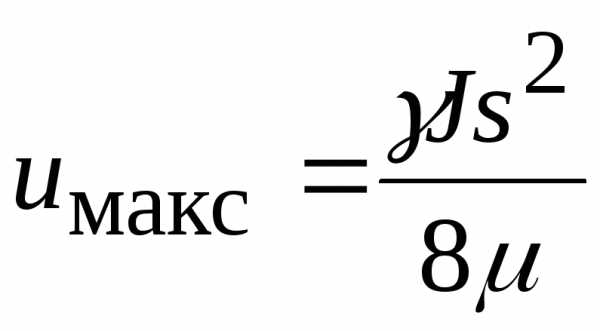
|
| Для определения расхода жидкостичерез щель выделим в ней элементарный слой толщиной |
Площадь выделенного слоя , скорость , расход
, расход
Проинтегрируем по всему потоку, вследствие симметрии потока при интегрировании от 0 до  результат нужно удвоить.
результат нужно удвоить.
Вспомним, что 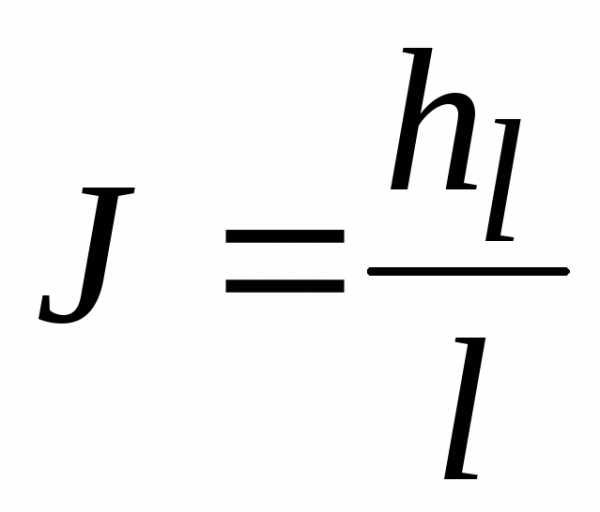 и
и
Расход через узкую щель 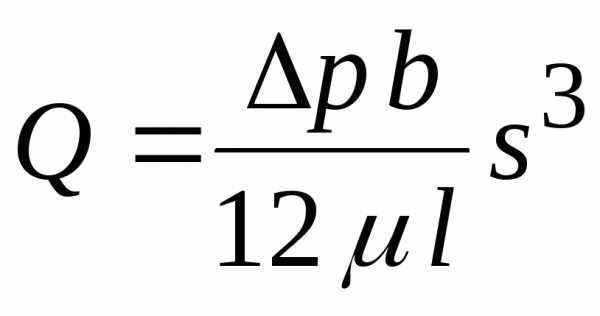
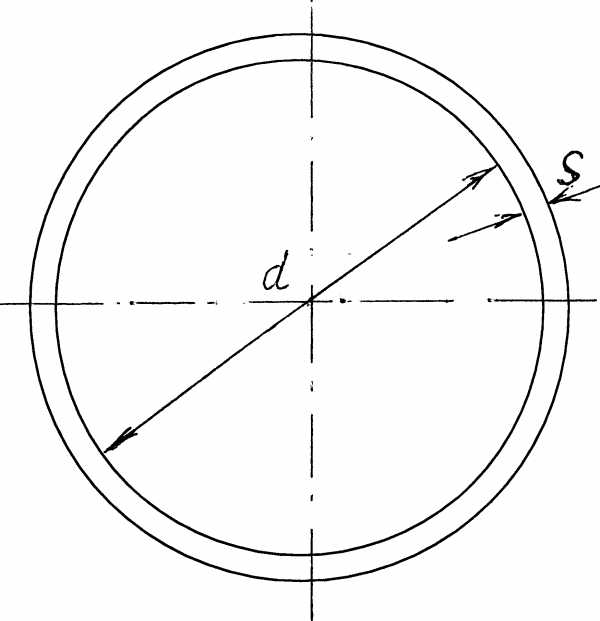
Замечание: утечки через зазор пропорциональны ширине в третье степени, т.е. при увеличении зазора в 2 раза утечки возрастают в 8 раз.
|
| Утечки через зазор в поршневой паре (диаметр поршня
|
При несимметричном расположении поршня в зазоре (при наличии эксцентриситета)
расход увеличивается и при максимальном эксцентриситете .
конец раздела 14
1Вычисление сводится к алгебраическим преобразованиям, не представляющим интереса в данном курсе. Вычислим отдельно числитель и знаменатель.
Для числителя используем скорость  элементарная площадь.
элементарная площадь.
Формула сокращенного умножения Числитель =
Знаменатель =  . Очевидно знаменатель в 2 раза меньше числителя.
. Очевидно знаменатель в 2 раза меньше числителя.
studfiles.net
Ламинарный режим - Справочник химика 21
Ламинарный режим имеет место при Не скорость осаждения определяется законом Стокса, так как коэффициент сопротивления [c.26]Величина критерия Рейнольдса, соответствующая смене режима движения, называется критической, ее принимают равной 2300 (Ке р = 2300). При Ке .2300 — турбулентный. Для труб некруглого сечения вместо с1 подставляют эквивалентный диаметр [см. уравнение (II, 34, а) ]. [c.46]
Ламинарный режим течения неньютоновских жидкостей в прямых трубах круглого сечения. [c.413]Рассмотрим вначале обогрев с помощью насыщенных паров теплоносителей, причем применительно к реакторам с греющими рубашками, т. е. применительно к условиям конденсации паров на вертикальной стенке. При этом, как известно (2, 15, 16], возможны три режима конденсатной пленки чисто ламинарный режим, т. е. режим, при котором критерий Рейнольдса для стекающей конденсатной пленки Ке меньше его критического значения Ке р, ламинарный по критерию Ке режим, но в котором возможно волнообразное течение, и, наконец, турбулентный режим, для которого справедливо соотношение Не >Ке . [c.58]
Течение жидкости в трубопроводе характеризуется режимом (ламинарный или турбулентный) и потерями давления. При малых скоростях наблюдается ламинарный режим, а при больших— турбулентный. Переход от одного режима к другому определяется по величине числа Рейнольдса при Ке 2320 — ламинарный, а при Ке > 2320 — турбулентный. Потеря давления (или перепад давления) вызывается сопротивлением движению жидкости за счет трения, вязкости и шероховатости поверхности труб. Для ньютоновских жидкостей в турбулентном режиме перепад давления, коэффициент сопротивления и другие параметры, характеризующие течение, связаны уравнением Бернулли [741 [c.274]
Оценим значение числа Рейнольдса для аппарата с горизонтальным потоком сырья, если d = 3 м, / = 18 м, m = 1 об/ч, v = =0,1 см /с. Подставляя эти значения в (7.22), получим Re op = 1330. Поскольку автору неизвестны исследования по определению критического числа Рейнольдса для течения жидкости через емкости типа рассматриваемых отстойников, нельзя точно установить, насколько найденная величина числа Re далека от критической. Однако в первом приближении Re p можно принять равным Rej,p для течения жидкости в круглых трубах, которое примерно равно 2300. Таким образом, когда ламинарный режим отстоя может смениться турбулентным, режимы нормальной эксплуатации отстойников довольно близки к критическим. Этому переходу будут способствовать неоднородность течения вдоль отстойника (особенно в районе входного и выходного маточника) и различного рода гидравлические возмущения, поступающие по системе подачи сырья. [c.133]
Опытным путем найдено, что ламинарный режим движения воздуха в порах осадка сохраняется до тех пор, пока значение модифицированного числа Рейнольдса R m не превысит 100. Величину этого числа находят из равенства [c.276]
В формуле (70) величина постоянной С зависит от направления теплового потока. В обычном промышленном теплообменном оборудовании ламинарный режим течения имеет место только в случае применения весьма вязких жидкостей. Вязкость таких жидкостей обычно сильно зависит от температуры. Вследствие этого в случае охлаждения слой жидкости, примыкающий к стенке и имеющий более низкую температуру, будет значительно более вязким и значительно более толстым, чем при нагреве, когда именно этот слой имеет наиболее высокую температуру. Следует иметь в виду, что примыкающий в стенке слой жидкости оказывает определяющее влияние на величину термического сопротивления, так как в непосредственной близости к стенке теплопередача может совершаться только благодаря теплопроводности. [c.57]
При увеличении частоты вращения вместо двух устойчивых циркуляционных контуров (ламинарный режим течения) наступает нестабильный режим течения с несколькими хаотично перемещающимися центрами вторичной циркуляции (переходный режим течения)— [c.279]
Для процесса отстаивания требуется определенное время, достаточное для осаждения взвешенных частиц и капелек воды на дно аппарата, и вместе с тем соответствующая скорость движения жидкости через отстойник, обусловливающая ламинарный режим потока. [c.277]
График показывает, что Язф критерия Рейнольдса эта разность сначала увеличивается, а потом остается неизменной. Рост эффективной теплопроводности является следствием увеличения турбулентной диффузии. [c.76]
Только для мелких частиц (ламинарный режим) для круп- [c.361]
Например, для потока жидкостей при (Ь/ )Ке >200 (ламинарный режим) имеем [c.62]
На рис. VH-7 в безразмерных координатах Тоб/Сов—1 воз/Своз показаны кривые для различных значений гПо- При построении этих кривых были приняты средние значения /=4,0 и у=2,5. Из рис. VH-7 можно быстро определить объем воздуха, продуваемого через осадок поверхностью 1 м при обезвоживании (ламинарный режим). [c.276]
При выполнении расчета целесообразно сначала определить объем воздуха, продуваемого во время каждой стадии процесса через осадок поверхностью 1 м (принимая ламинарный режим движения воздуха в порах), а затем найти общий объем продуваемого воздуха для всех стадий при тех же условиях и умножить этот общий объем на величину поправки /турб и величину поверхности фильтрования. [c.277]
Для пластичных жидкостей устойчивый ламинарный режим движения наблюдается при Re 2000, переходный режим соответствует 2000 3000 наступает турбулентный режим течения. [c.161]
Для каждой установки существует некоторый диапазон критических значений чисел Ке р, при которых происходит переход от одного режима течения к другому. Значение критического числа Ке, ниже которого режим течения обязательно ламинарный, для трубы круглого сечения составляет примерно 2300. Число Ке,(р, при котором ламинарный режим течения переходит в турбулентный, существенно зависит от условий входа потока в трубу, состояния поверхности стенок и др. При очень плавном входе и гладких стенках переход от ламинарного режима к турбулентному наступает при числах Ке, р > 2300. На практике чаще встречается турбулентный режим течения. [c.19]
I вариант — ламинарный режим 0,064 0,287.10- [c.200]
Полученное числовое значение критерия Рейнольдса указывает на ламинарный режим движения теплоносителя и на необходимость расчета коэффи-диента теплоотдачи от конденсата к наружной поверхности пучка по уравнению [38, с. 100] [c.182]
Основное влияние на гидродинамический режим процесса отстоя в дегидраторе оказывает тип ввода сырья. В гл. 6 было показано, что в настоящее время в отстойниках используют вводы трех основных типов нижний, торцевой и через распределительные головки. Наиболее просто определить ПФ для отстойника с вводом сырья через распределительное устройство, расположенное в нижней части аппарата, и отбором сырья из верхней части аппарата (см. рис. 2.5, с. 29). В этом случае капли будут двигаться против потока нефти. Поэтому абсолютная скорость осаждения капли объемом V сложится из скорости движения сплошной фазы к , направленной вверх, и скорости осаждения капли (У), направленной вниз. Если в отстойной части аппарата соблюдается ламинарный режим движения жидкости, то все капли, для которых скорость сплошной фазы больше скорости их осаждения, не осядут и останутся в товарной нефти. Поэтому будет справедливо равенство [c.127]
С увеличением скорости на тыльной стороне трубы начинают развиваться интенсивные завихрения, приводящие к турбулизации потока. Опыты, проведенные Чилтоном [142], показали, что ламинарный режим в поперечном потоке сохраняется лишь при Ре [c.110]
Ламинарный режим движения жидкости у вертикальной стенки Локальное 10 -103 0,6 0,25 [c.116]
Ламинарный режим течения (от латинского слова ламина — слой) наблюдается при малых скоростях движения или большой вязкости жидкости (рис. П-11, а). При этом жидкость движется как бы параллельными струйками, которые н смешиваются одна с другой. [c.45]
Уменьшение сопротивлений мас-со- и теплопереносу, лимитирующих скорость превращения. В некоторых случаях (см. раздел VIII) скорости массо- или теплопереноса через границу раздела фаз определяют скорость превращения. Ламинарная пограничная пленка оказывает основное сопротивление этим процессам, поскольку перенос массы через нее осуществляется только диффузией, а перенос теплоты — теплопроводностью, т. е. относительно медленно. За этой пленкой перенос массы и теплоты происходит главным образом конвекцией. Чем больше толщина пограничной пленки, тем выше сопротивление. В связи с этим наименее выгоден ламинарный режим движения потоков в системе. При высокой турбулентности потоков толщина пограничной ламинарной пленки меньше и, следовательно, легче и более быстро осуществляется транспорт массы и теплоты в другую фазу. [c.414]
В промышленных теплообменниках ламинарный режим движения потоков в трубах встречается редко. [c.183]
При осаждении мелких частиц, а также в случае большой вязкости среды скорость движения частиц мала, вихри не образуются и основную роль играют силы трения (ламинарный режим). [c.322]
Поскольку в электрофильтре осаждаются мелкие частицы, может быть принят ламинарный режим нх движения. Тогда скорость [c.353]
Если Ог Рг = 500-f-2 10 (ламинарный режим) [c.567]
Из-за бесконечного расширения струи и ее обмена импульсом с неподвижной окружающей средой ускоряющаяся горизонтальная составляющая скорости должна в конечном счете преобразоваться в замедляющееся течение пристенной струи. Таким образом, составляющая скорости и>х(а г) параллельная стенке, первоначально линейно увеличивающаяся от нуля, должна достигнуть максимального значения на определенном расстоянии Xg rg) от критической точки и в конце концов устремляется к нулю как в полностью развитой пристенной струе. Экспонента п приблизительно равна 0,5 для плоской [8, 10, 11] и 1 для осесимметричной [8, И, 12] турбулентной пристенной струи. Поскольку стабилизирующее влияние ускорения поддерживает ламинарным режим течения в пограничном слое, в зоне формирования потока переход к турбулентному режиму течения в общем случае будет происходить сразу после (или г ) в области замедления потока. Пристенный пограничный слой и граница свободной струи растут вместе, формируя типичный профиль пристенной струи, [c.268]
Решения и корреляционные соотношения для постоянной температуры стенки. J. Ламинарный режим течения. Следующие асимптотические решения получены в [10] для ламинарного режима течения в пограничном слое [c.275]
Различают два режима течения жидкости — ламинарный и турбулентный. Ламинарный режим течения является устойчивым, струйки жидкости движутся отдельно, не смешиваясь одна с другой. Турбулентный режим характеризуется неустойчивостью течения, бe пopяJl,oчным перемещением конечных масс жидкости и их перемешиванием. [c.19]
Числа Рейнольдса, при которых может возникнуть переходный режим течения, существенно изменяются в зависимости от типа пластин. Как правила, во всех типах пластинчатых теплообменников турбулентный режим течения возникает при числах Рейнольдса, превышающих 1000, и ламинарный режим — при числах Рейнольдса до 10. При значениях чисел Рейнольдса между этими предельными значениями характеристики теплообменника рассчитываются очень приближенно, и почти всегда необходима экспериментальная проверка результатов расчета. [c.83]
Автор рассматривает ламинарный режим обтекания частицы газовым потоком. При этом выражение (XIV,7) записано с ошибкой. Анализ неравномерного движения твердой частицы приводит к уравненшо [c.558]
Режимы течения. Рейнольдс опытным путем установил, что в движущемся потоке жидкости или газа можно отчётливо различить два режима течения. Они получили названия ламинарный и турбулентный. При первом режиме слои жидкости скользят друг по другу и отдельные частицы движутся по непересекающимся траекториям. При турбулентном режиме, напротив, частицы движутся неупорядоченно, хаотически, а отдельные слои жидкости перемешиваются друг с другом, образуя вихри. Было также установлено, что при-достижении величиной Ке = ш//у (названной позднее критерием Рейнольдса) некоторого критического значения ламинарный режим начинает сменяться турбулентным. Здесь I представляет собой некоторый характерный линейный размер. Для потока жидкости или газа внутри труб принято использовать в качестве характерного размера I внутренний диаметр трубы в. В этом случае Некр = 2100. [c.65]
Вязкость теплоносителя. Согласно обш,ему правилу теплоноситель с большой вязкостью должен быть помещен в межтрубное пространство, так как турбулизация потока, обусловленная поперечным обтеканием пучков труб, будет способствовать увеличению теплоотдачи. Одпако если и потоке со ст( роны коэкуха все же сохряияЕ тся ламинарный режим течения, то следует рассмотреть вариант с течением этого тенлоносителя в трубах. [c.29]
Осаждаемые под действием злеш рического поля частицы движутся с малой скоростью, поэтому нрн определении скорости осаждения частицы можно принять заведомо ламинарный режим ее движения. [c.63]
chem21.info
Ламинарный режим - Большая Энциклопедия Нефти и Газа, статья, страница 1
Ламинарный режим
Cтраница 1
Ламинарный режим наблюдается при малых скоростях движения жидкости. [2]
Ламинарный режим имеет место вокруг стержня и в ( Восходящем потоке воздуха на значительном расстоянии от поверхности стенки. При больших диаметрах тела турбулентное течение может развиться не только вне тела, но и на его верхней части. [3]
Ламинарный режим может временно сохраняться и при Re 2100, если труба, по которой течет жидкость, очень гладкая и в системе отсутствуют вибрации. Если же внутренняя поверхность трубы имеет заметные шероховатости или система подвержена действию каких-либо внешних возмущений, внутри ламинарного потока наблюдается хаотическое движение, которое, в конечном счете, приведет к возникновению турбулентности. [4]
Ламинарный режим может существовать при протекании жидкости в трубах и щелях малого сечения, в капиллярах, в смазочном слое гидродинамических подшипников. [5]
Ламинарный режим характеризуется параллельно струйным упорядоченным движением частиц жидкости. Для этого режима движения все основные закономерности могут быть установлены не только экспериментально, но и выведены аналитически. [7]
Ламинарный режим сохраняется до Re 2320; при 2320 Re 2800 существует так называемый переходный режим. [8]
Ламинарные режимы имеют место в пленочных теплообменниках при стенании конден-сатной пленки под действием силы тяжести, в трубчатых теплообменниках при малых скоростях движения воды в трубках, при движении нефти и масел по трубопроводам, грунтовых потоков, лавы, крови в мелких кровеносных сосудах. [9]
Ламинарный режим возможен лишь в случае потоков малого сечения и малых средних скоростей v жидкости, имеющей значительную вязкость. [10]
Ламинарные режимы, применяемые в таких горелках, делают их приборами весьма умеренных форсирово К. Если по тем или иным причинам возникнет стремление к созданию диффузионных горелок малых форсировок с сильно укороченными факелами, то может быть с успехом применен принцип, вполне аналогичный принципу беспламенных горелок кинетического типа с заменой единичных газовых и воздушных каналов множеством параллельных канальцев. В этом случае, несмотря на столь вялое смесеобразование, какое возникает за счет молекулярной диффузии, диффузионные факелы с ничтожными поперечными размерами получат и ничтожную протяженность, хотя и заметно большую, чем при кинетическом принципе горения. [11]
Ламинарный режим характеризуется упорядоченным движением, при котором жидкость движется в виде отдельных струек, параллельных поверхности твердого тела без перемешивания. Поперечное перемещение частиц практически отсутствует, и, следовательно, общее движение жидкости совпадает с частным движением отдельных ее частиц. [12]
Ламинарный режим преобладает при низких скоростях. Поток упорядоченный, зависимость давление - скорость является функцией вязкостных свойств жидкости. [13]
Ламинарный режим с точки зрения проведенного анализа обладает одним важным качеством: при равномерном движении жидкости все ее частицы движутся без ускорения. Следовательно, инерционные свойства жидкости не должны проявляться. [14]
Ламинарный режим можно рассматривать как совокупность независимых друг от друга ( замкнутых) перемещающихся мини-реакторов. В установившемся режиме подачи реагентов и отвода смеси продуктов из реактора, характерной будет неизменность концентраций реагентов и продуктов в каждом сечении реактора. Кинетическое описание процессов в подобном реакторе идеального вытеснения практически не отличается от такового для замкнутых систем. Измеряя концентрационную характеристику в вы & ранном сечении реактора, ее относят к времени t, выраженному как г / и где г - расстояние от начала реактора, и - линейная скорость движения фронта потока вдоль реактора. [15]
Страницы: 1 2 3 4 5
www.ngpedia.ru
Ламинарный режим - течение - Большая Энциклопедия Нефти и Газа, статья, страница 1
Ламинарный режим - течение
Cтраница 1
Ламинарный режим течения имеет место только при числах Рейнольдса, меньших своего критического значения. Однако необходимо иметь в виду, что величина RKp в значительной мере зависит от условий течения и в первую очередь от начальной турбулентности втекающего потока. В специальных экспериментах, где турбулентность внешнего потока была незначительной, удалось сохранить ламинарный режим течения до значительно больших, чем критическое, значений чисел Рейнольдса. [2]
Ламинарный режим течения ( движения) жидкости - это такой режим течения, при котором частицы жидкости перемещаются по траекториям, направленным вдоль общего основного течения, без поперечного перемещения; пульсации давле - ння и скорости отсутствуют. [3]
Ламинарный режим течения имеет место только при числах Рейнольдса, меньших своего критического значения. Однако необходимо иметь в виду, что величина RKp в значительной мере зависит от условий течения и в первую очередь от начальной турбулентности втекающего потока. В специальных экспериментах, где турбулентность внешнего потока была незначительной, удалось сохранить ламинарный режим течения до значительно больших, чем критическое, значений чисел Рейнольдса. [5]
Ламинарный режим течения реализуется при сравнительно малых числах Рейнольдса, меньших некоторого критического значения, называемого критическим числом Рейнольдса ReKp. При Re ReKp течение имеет турбулентный характер. [6]
Ламинарный режим течения в трубах заканчивается при значении критерия Re 2300, интервалу 2300; Re; 10 000 соответствует переходная область от ламинарного режима течения к турбулентному; при Re 10000 начинается развитый турбулентный режим течения. [8]
Ламинарный режим течения характерен, главным образом, для вязких жидкостей ( нефть, мазут, минеральные масла и пр. В санитарно-технической практике ламинарное течение иногда приходится наблюдать на малых объектах водяного отопления и внутридомового газопровода. [9]
Ламинарный режим течения реализуется при сравнительно малых числах Рейнольдса, меньших некоторого критического значения называемого критическим числом Рейнольдса Кбкр. При Re ReKp течение имеет турбулентный характер. [10]
Ламинарный режим течения наблюдается при ReReKp. [12]
Ламинарный режим течения потока, рассматриваемый выше, далеко не всегда соответствует реальным условиям работы массообменной технологической аппаратуры. [13]
Однако ламинарный режим течения теряет внутреннюю устойчивость при возрастании в потоке инерционных сил по сравнению с силами вязкого трения. [14]
Принят ламинарный режим течения, сопротивление считается по формуле Пуазейля. [15]
Страницы: 1 2 3 4 5
www.ngpedia.ru
4.3. Ламинарный режим движения жидкости.
4.3.1.Распределение скоростей, касательных напряжений. Средняя скорость. Коэффициент Дарси. Закон Пуазейля.
Ламинарный режим характеризуется параллельноструйным упорядоченным движением частиц жидкости. Для этого режима все основные закономерности могут быть выведены аналитически.
1).Закон распределения скоростей по сечению.
Рассмотрим ламинарное установившееся равномерное движение жидкости в круглой трубе радиусом r0.
Выделим в этом потоке вокруг его оси объем жидкости в виде цилиндра длиной l и радиусом r. При движении этого цилиндра на его боковой поверхности возникает сила внутреннего трения Т, которая может быть найдена из закона вязкого трения Ньютона:  , где
, где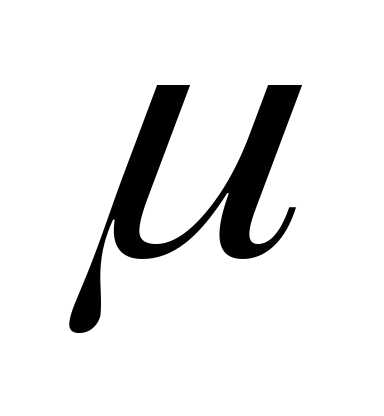 -динамический коэффициент вязкости, равный,S – боковая поверхность, которая в рассматриваемом случае равна боковой поверхности цилиндра S=2лrl. Знак «—» в уравнении принят потому, что du/dr отрицательно (с увеличением расстояния от оси потока у скорость частиц жидкости и уменьшается).
-динамический коэффициент вязкости, равный,S – боковая поверхность, которая в рассматриваемом случае равна боковой поверхности цилиндра S=2лrl. Знак «—» в уравнении принят потому, что du/dr отрицательно (с увеличением расстояния от оси потока у скорость частиц жидкости и уменьшается).
Движущими силами в данном случае являются силы давления, равнодействующая которых будет
П ри равномерном движенииТ=
ри равномерном движенииТ= Р или.
Р или.
Заменим (р1—р2) его значением через потери давления:. Сделав в полученном уравнении сокращения и разделив переменные, получим
или далее 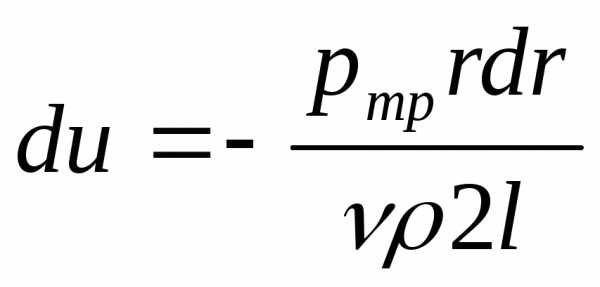
или после интегрирования
|
| (4.10) |
Для нахождения постоянной интегрирования зададимся начальными условиями: при r=r0, т. е. у стенки трубы, вследствие прилипания частиц жидкости u = 0. Тогда:
 , отсюда
, отсюда  .
.
Подставляя значение С в (4.10), получим закон распределения скоростей по сечению круглой трубы при ламинарном режиме движения, установленный английским физиком Дж. Стоксом:
|
| (4.11) |
При у = 0, т. е. на оси трубы, u=umах
| | (4.12) |
Таким образом, полученное уравнение является уравнением параболоида вращения с вершиной, лежащей на оси трубы. Следовательно, при ламинарном режиме движения эпюра скоростей по сечению будет иметь форму параболы (на рис 30.)
2) Закон распределения касательных напряжений.
Подставив в (13) значение du/dr, можно установить также закон изменения касательных напряжений вдоль радиуса:
|
| (4.13) |
Из формулы видно, что при ламинарном режиме движения жидкости изменение  вдоль радиуса происходит по линейному закону, причем
вдоль радиуса происходит по линейному закону, причем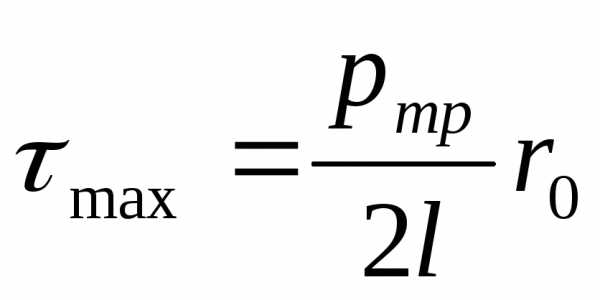 будет при r = r0, т. е. у стенки трубы, a
будет при r = r0, т. е. у стенки трубы, a 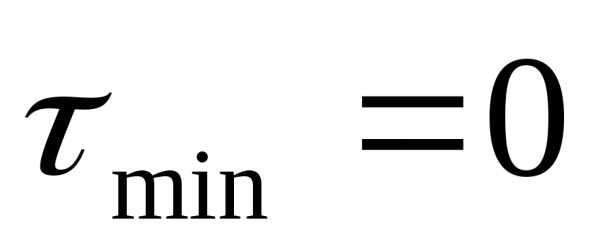 будет приr = 0, т. е. на оси трубы.
будет приr = 0, т. е. на оси трубы.
3). Расход и средняя скорость потока.
Для определения расхода Q выделим в поперечном сечении потока элементарное живое сечение кольцевой формы радиуса r и шириной dr. Элементарный расход жидкости через это сечение будет
dQ = udS,
где u - скорость жидкости в кольцевом сечении,
dS — элементарное живое сечение dS = 2 rdr. Тогда
rdr. Тогда
| (4.14) |
Средняя скорость при ламинарном потоке в круглой трубе.
| | (4.15) |
4). Коэффициент Кориолиса.
Так как при ламинарном режиме движения закон распределения скоростей по сечению известен и может быть выражен аналитически, то и коэффициент Кориолиса а может быть вычислен непосредственно по уравнению:  .
.
Заменим в этом уравнении u и r их значениями из предыдущих формул, а dS и S — принятыми выше значениями: dS = 2 rdr и S =
rdr и S = .
.
После подстановки указанных параметров произведем сокращения и интегрирование полученного выражения:
| | (4.16) |
Таким образом, результаты аналитического определения коэффициента а при ламинарном режиме движения полностью согласуются с опытными данными.
4). Закон гидравлического сопротивления. Коэффициент Дарси.
Для получения закона сопротивления, т. е. выражения потери напора на трение hтр через расход и размеры трубы, определим pтр из формулы
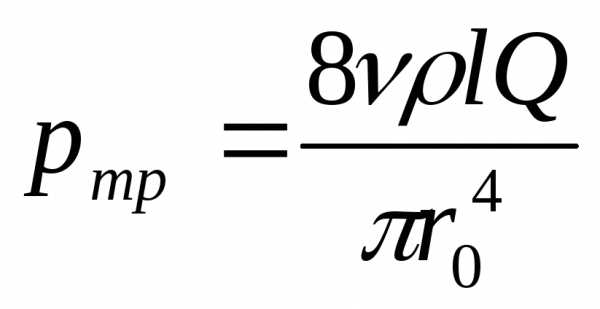 , тогда .
, тогда .
Полученный закон сопротивления показывает, что при ламинарном течении в круглой трубе потеря напора на трение пропорциональна расходу (скорости) и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто именуемый законом Пуазейля-Гагена, используется для расчетов трубопроводов с ламинарным режимом течения.
Условимся потери напора на трение выражать через среднюю скорость по формуле:
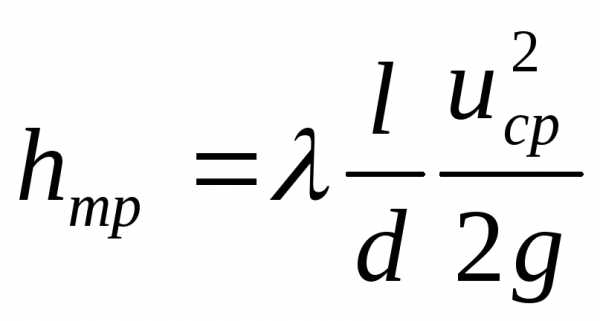 .
.
Приведем закон сопротивления к общепринятому виду. Для этого в формуле заменим расход через произведение  ; получим
; получим
| | (4.17) |
Перемножив и разделив правую часть уравнения на 2ucр после перегруппировки множителей получим
 .
.
Откуда можно найти
| | (4.18) |
Последнее выражение носит названия коэффициента Дарси. Индекс «л» указывает, что коэффициент сопротивления трению вычисляется именно при ламинарном течении.
studfiles.net
Ламинарный режим - движение - Большая Энциклопедия Нефти и Газа, статья, страница 1
Ламинарный режим - движение
Cтраница 1
Ламинарный режим движения проявляется в том, что при фильтрации расход и скорость связаны с потерями напора линейной зависимостью. [1]
Ламинарный режим движения был впервые изучен более 100 лет тому назад Гагеном и Пуазейлем. [2]
Ламинарный режим движения является автомодельным - не зависимым от определяющего параметра - числа Рейнольдса. Однако, турбулентное движение, строго говоря, при любых числах Рейнольдса ( ReReKp) неавтомодельно, хотя при очень больших числах Рейнольдса это движение принимают приближенно автомодельным. [3]
Ламинарный режим движения нефтепродуктов встречается крайне редко, в основном при перекачке высоковязких нефтей. [4]
Ламинарный режим движения воздуха около поверхности испарения наблюдается при 2 - 102 GrPr ( GrPr) Kp. Верхний предел рассматриваемого режима зависит от формы поверхности испарения и условий протекания процесса испарения. [5]
Ламинарный режим движения пленки жидкости, для которого выведено уравнение ( IV. II, устойчив лишь при сравнительно малых расходах жидкости. Даже при относительно небольших значениях Re волновое течение ламинарной пленки является более устойчивым, чем струйное. [6]
Особенностью ламинарного режима движения является то, что потери напора по длине прямо пропорциональны вязкости жидкости и средней скорости в первой степени и не зависят от шероховатости и, следовательно, материала стенок трубы. [8]
Переход ламинарного режима движения в турбулентный происходит постепенно, поэтому обычным является переходный режим движения. Режим движения жидкости оказывает большое влияние на гидравлические потери. В связи с этим всегда требуется точное знание условий смены режима течения. Как оказывает опыт, переход ламинарного режима в турбулентный зависит от скорости движения, вязкости жидкости, а также от диаметра трубы. [9]
Переход ламинарного режима движения в турбулентный не определяется каким-либо одним значением числа Рейнольдса. [10]
Область ламинарного режима движения - с увеличением числа Re коэффициент К уменьшается. [12]
При ламинарном режиме движения практически отсутствуют пульсации скорости ( ет 0) и касательные напряжения зависят от вязкости жидкости - и градиента скорости, но не зависят от шероховатости стенок русла. [13]
При ламинарном режиме движения ускорение равно нулю, и величина р несущественна. Из опыта известно, что величина А при этом режиме также несущественна. [14]
При ламинарном режиме движения существуют лишь продольные составляющие скоростей. [15]
Страницы: 1 2 3 4
www.ngpedia.ru

 .
.
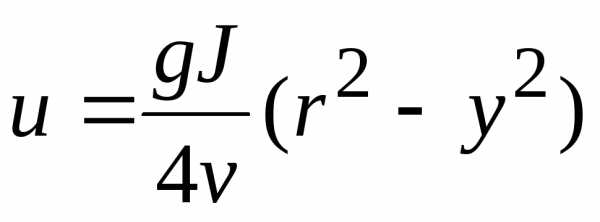


 , расположенный симметрично по центру зазора.
, расположенный симметрично по центру зазора.
 , отстоящий от оси потока на расстояние
, отстоящий от оси потока на расстояние .
.
 , величина зазора
, величина зазора )
)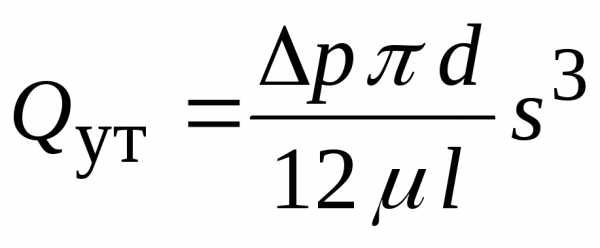
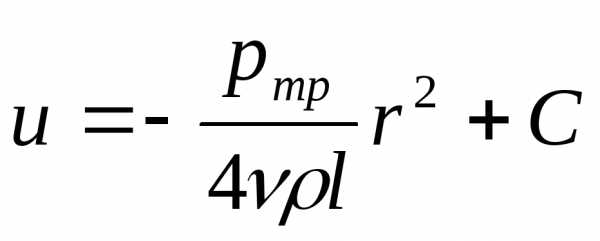 .
.