ГлавнаяРазноеНайти расстояние от точки до плоскости

Нахождение расстояния от точки до плоскости. 11-й класс. Найти расстояние от точки до плоскости


Определение расстояния от точки до плоскости

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость, и в начертательной геометрии определяется графически согласно следующему алгоритму.

Алгоритм построения

  1. Плоскость переводят в проецирующее положение с помощью методов преобразования ортогональных проекций.
  2. Из точки на плоскость опускают перпендикуляр и находят его длину. Направление проекции перпендикуляра определяется на основании теоремы о проецировании прямого угла.

Задача № 1

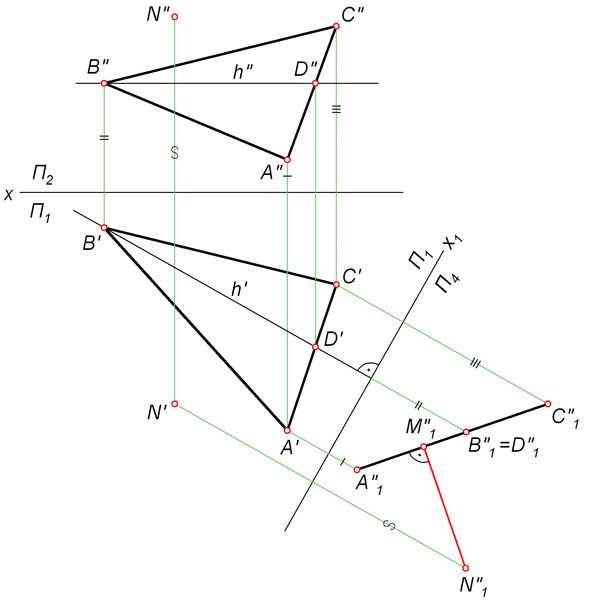
Рассмотрим, как реализуется составленный нами алгоритм на практике. На рисунке ниже представлены графические построения, необходимые для определения расстояния между точкой N и плоскостью α, заданной треугольником ABC.

Ход решения

Задача № 2

Требуется определить величину расстояния между точкой K и плоскостью β, заданной следами. В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h0β.

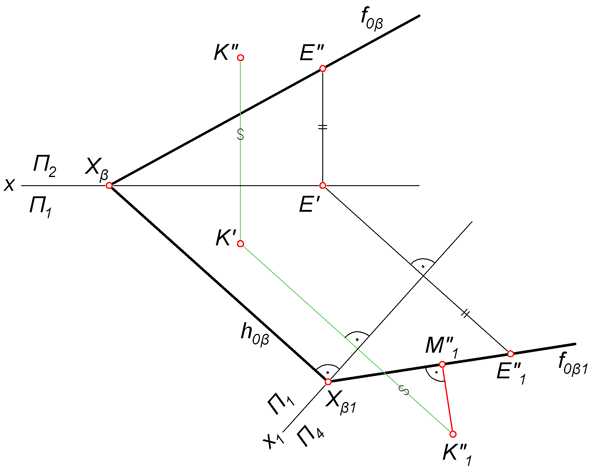
Ход решения

Если требуется перевести отрезок KM в исходную систему плоскостей, то это делается с помощью обратных преобразований, как показано на следующем рисунке.

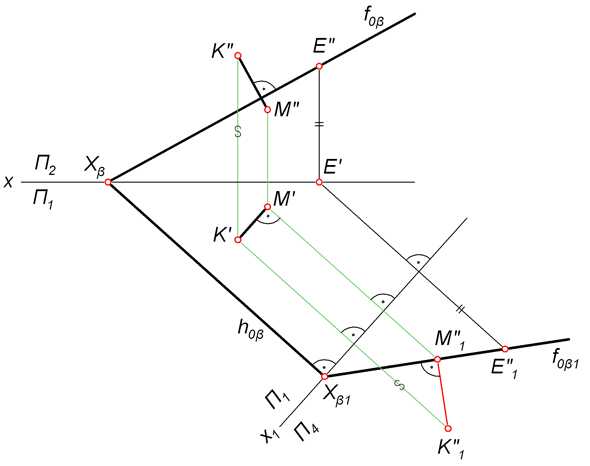
Похожие задачи:

ngeometry.ru

Вычисление расстояния от точки до плоскости

Реферат

по алгебре и геометрии

Вычисление расстояния между линейными геометрическими объектами в пространстве

студента группы КБ-12

Никитченко Богдана

Вычисление расстояния от точки до плоскости

Первый способ

Расстояние от точки до плоскости находим по следующей формуле:

d= , где - длина вектора нормалиN={A;B:C} плоскости α, а число есть результат подстановки координат точкиM1(x1; y1; z1) в левую часть общего уравнения плоскости.

Пример ( Клетеник № 959(5)):

Вычислить расстояние d от точки M5(9;2;-2) до плоскости 12y-5z+5=0.

Решение:

N= {0; 12; -5}

d= = 3

Ответ: 3

Второй способ

Составляем уравнение прямой L, которая проходит через точку М1 и перпендикулярна к плоскости α.

Находим координаты  точки M0(x0; y0; z0) - точки пересечения прямой L и плоскости α.

Вычисляем расстояние между точками M0 и М1  по формуле:

d= M0M1 = (x1-x0)2 + (y1-y0)2 + (z1-z0)2

Пример ( Клетеник № 959(4)):

Вычислить расстояние d от точки M4(3;-6;7) до плоскости 4x-3z-1=0.

Решение:

L:

4(4t+3) -3(-3t+7) =0

16t +12 +9t -21-1=0

25t=10

t=0,4

x0= 4•0,4+3=4,6

y0= - 6

z0= -3•0,4+7=5,8

M0(4,6; -6; 5,8)

d==2

Ответ: 2

Вычисление расстояния между параллельными плоскостями

Первый способ

Выберем любую точку на первой плоскости.

Применим формулу расстояния от точки до плоскости.

d=

Пример (Клетеник № 964(5)):

Вычислить расстояние между параллельными плоскостями:

30x-32y+24z-75=0 15x-16y+12z-25=0

Решение:

Пусть y=0 и z=0. Тогда подставив эти значения в первое уравнение, получим

x=2,5. Мы получили точку М(2,5; 0; 0) . Применим формулу расстояния от точки до плоскости: d= =0,5

Ответ: 0,5

Второй способ

Если плоскость α задана уравнением Ax + By + Cz + D1=0 , а плоскость β задана уравнением Ax + By + Cz + D2=0, то расстояние между параллельными плоскостями находим по следующей формуле:

d=

Пример( Клетеник №964(6)):

Вычислить расстояние между параллельными плоскостями:

6x-18y-9z-28=0 4x-12y-6z-7=0

Решение:

Умножив обе части второго уравнения на , получим 6x-18y-9z-10,5=0.

Применим формулу: d= =

Ответ:

Вычисление расстояния от точки до прямой в пространстве

Первый способ

Определим направляющий вектор прямой a ={ l; m; n}и вычислим его длину по формуле a =

Найдем координаты некоторой точки М0(x0; y0; z0), лежащей на прямой a. Вычислим координаты вектора M0M1={x1-x0; y1-y0; z1-z0}, найдем векторное произведение векторов a и M0M1 и его длину.

Найдем расстояние от точки до прямой в пространстве по формуле:

d(M1;L)=

Пример (Клетеник №1063(1)):

Вычислить расстояние d от точки P(2; 3; -1) до прямой:

= =

Решение:

a = {3; 2; -2}

a ==

M0(5; 0; -25) M0P = {-3; 3; 24}

a x M 0P = = 54i – 66j + 15k

a x M 0P = =21

d= 21=21

Ответ: 21

Второй способ

Составляем уравнение плоскости α , проходящей через данную точку М1(x1; y1; z1) перпендикулярно к данной прямой L.

Определяем координаты M0(x0; y0; z0) – точки пересечения прямой  L и плоскости α .

Находим расстояние от точки М1до прямой L по формуле:

d= (x1-x0)2 + (y1-y0)2 + (z1-z0)2

Пример(Клетеник №1063(2)):

Вычислить расстояние d от точки P(2; 3; -1) до прямой:

Решение:

Составим уравнение плоскости, проходящей через точку P(2; 3; -1) с вектором нормали a={1; 1; 4}.

(x-2) + (y-3) +4(z+1)=0

x+y+4z-1=0

Найдем точку пересечения прямой и плоскости

(t+1)+(t+2)+4(4t+13)-1=0

t+1+t+2+16t+52-1=0

18t=-54

t= -3

M0(-2; -1; 1) - точка пересечения прямой   и плоскости.

d==6

Ответ: 6

Вычисление расстояния между параллельными прямыми

Выберем на одной из прямых любую точку.

Применим формулу расстояния от точки до прямой:

d(M1;L)=

Пример(Клетеник № 1064):

Убедившись, что прямые параллельны, вычислить расстояние d между ними.

Решение:

Перейдем от общих уравнений прямой к каноническому.

Найдем точку M0(x0; y0; z0)

Пусть z0=0. Тогда подставим это значение в общие уравнения прямой.

4x=54

x=13,5

y= -8,5

M0(13,5; -8,5; 0)

a1 =N1 x N2== -3i+j-4k

a 1={-3,1,-4} a 2={3,-1,4}

Векторы a1и a2 коллинеарны. Следовательно прямые параллельны.

Из уравнения второй прямой находим M1(-7; 5; 9).

M0M1={-20,5; 13,5; 9}

a1 x M0M1==63i+109j-20k

a1 =

a1 x M0M1 =

d= =25

Ответ: 25

Вычисление расстояния между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми находим по формуле: d(L1;L2)=, гдеa1,a2 – направляющие векторы прямых, M1, M2–точки на прямых L1 и L2.

Если числитель равен нулю, то прямые пересекаются.

Пример (Клетеник №1083(3)):

Вычислить кратчайшее расстояние между двумя прямыми: = =

Решение:

a1 x a2 = =-6i-9j-18k

a1 x a2 = 21

M1(-5; -5; 1) M2(9; 0; 2)

M2M1={14; 5; 1}

a1 a2 M2M1 = -84 – 45 -18 =147

d==7

Ответ: 7

studfiles.net

Расстояние от точки до плоскости. Метод координат. Задание 14

Расстояние от точки до плоскости. Метод координат. Задание 14

В этой статье мы поговорим о том, как найти расстояние от точки до плоскости с помощью метода координат. О том как находить расстояние от точки до плоскости геометрическим способом, вы можете прочитать здесь.

Решим задачу: в единичном кубе найдите расстояние от точки до плоскости .

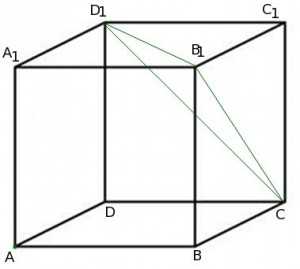
На этот раз давайте решим ее с помощью метода координат.

Сначала немного теории.

Рассстояние  от точки  до плоскости вычисляется по такой формуле:

Чтобы воспользоваться этой формулой, поместим наш куб в систему координат:

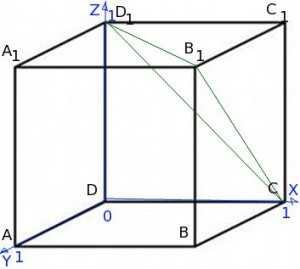В нашей задаче роль точки  играет точка . То есть ,  ,  

Теперь наша задача найти коэффициенты ,   ,   и в уравнении  плоскости .

Плоскость   определяется тремя точками  ,    и . Если мы координаты точек подставим в уравнение плоскости , то получим верное равенство.

Коэффициент  в уравнении плоскости мы можем принять равным 1.

Чтобы найти коэффициенты  ,   и  , подставим координаты точек  ,    и в уравнение плоскости . Получим систему уравнений:

Отсюда: ,  ,  

Подставим координаты точки  и значения коэффициентов в формулу для расстояния:

Ответ: 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Расстояние от точки до плоскости. Задание С2

В этой статье я хочу познакомить вас  с тремя способами нахождения расстояния от точки до плоскости. Какой из них выбирать при решении задачи, зависит от ее условия.

О четвертом, координатном методе нахождения расстояния от точки до плоскости я расскажу в следующей статье.

Решим задачу: В единичном кубе   найдите расстояние от точки  до плоскости :

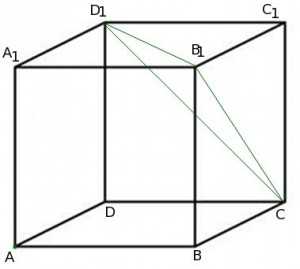Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.

Чтобы провести перпендикуляр из точки  к плоскости , проведем через точку  плоскость, перпендикулярную плоскости :

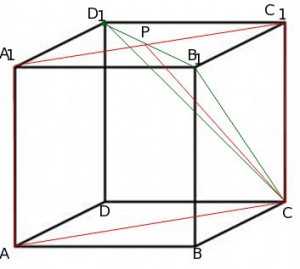Докажем, что плоскость   перпендикулярна плоскости :

1.  (как диагонали квадрата)

2.   (так как  перпендикулярна плоскости  и, значит, любой прямой, лежащей в этой плоскости)

3. Таким образом, прямая  перпендикулярна двум пересекающимся прямым плоскости    ( и ), и, следовательно, перпендикулярна плоскости . Значит, любая плоскость, проходящая через прямую  будет перпендикулярна плоскости , в том числе и плоскость .

- линия пересечения плоскости  и плоскости .

Рассмотрим треугольник  и в плоскости этого треугольника проведем высоту   к стороне :

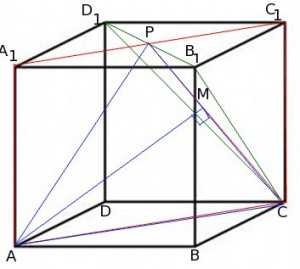
Начертим треугольник  отдельно:

Найдем  как гипотенузу прямоугольного треугольника :

Чтобы найти высоту , выразим два раза площадь треугольника:

Ответ: 

2 способ.

Рассмотрим правильную пирамиду с основанием  и вершиной :

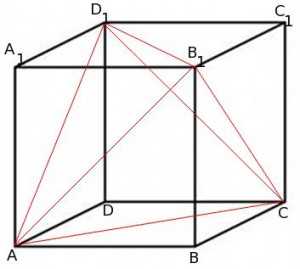Расстояние от точки  до плоскости  равно высоте пирамиды.

В основании пирамиды лежит правильный треугольник  стороны которого равны . Боковые ребра пирамиды также равны между собой и равны .

Если боковые ребра пирамиды равны между собой, то вершина проецируется в центр описанной около основания окружности  - в нашем случае ( в случае правильного треугольника) - это точка пересечения медиан.

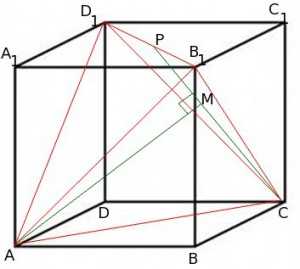
Точка M - точка пересечения медиан правильного треугольника делит медианы в отношении 2:1, считая от вершины.

найдем по теореме Пифагора из треугольника :

Ответ: 

Примечание. Если вершина пирамиды проецируется в центр описанной окружности, то высоту пирамиды можно найти по формуле:

, где  - высота пирамиды,  - длина бокового ребра,  - радиус окружности, описанной около основания.

Радиус описанной окружности удобно находить по теореме синусов: отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности

3. И еще один способ нахождение расстояния от точки до плоскости через объем. Рассмотрим тетраэдр . Он получается, если от куба  "отрезать"  4 одинаковые пирамиды, объем каждой из которых равен 1/6 объема куба. То есть мы "отрезаем"  2/3 объема куба и остается 1/3.

Площадь основания тетраэдра  равна площади треугольника  и равна 

Получаем: 

Отсюда 

И.В. Фельдман, репетитор по математике.

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Нахождение расстояния от точки до плоскости. 11-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (569,8 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

Оборудование:

ХОД ЗАНЯТИЯ

I. Организационный момент

II. Этап актуализации знаний (слайд 2)

Повторяем как определяется расстояние от точки до плоскости

III. Лекция (cлайды 3-15)

На занятии мы рассмотрим различные способы нахождения расстояния от точки до плоскости.

Первый метод: поэтапно-вычислительный

Расстояние от точки М до плоскости α: – равно расстоянию до плоскости α от произвольной точки Р, лежащей на прямой a, которая проходит через точку М и параллельна плоскости α; – равно расстоянию до плоскости α от произвольной точки Р, лежащей на плоскости β, которая проходит через точку М и параллельна плоскости α.

Решим следующие задачи:

№1. В кубе  А…D1  найти расстояние от точки С1 до плоскости АВ1С.

Решение.

Осталось вычислить значение длины отрезка О1Н.

№2. В правильной шестиугольной призме А…F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA1.

Решение:

Следующий метод: метод объемов.

Если объем пирамиды АВСМ  равен V, то расстояние от точки М до плоскости α, содержащей ∆АВС вычисляется по формуле ρ(М; α) = ρ(М; АВС) = При решении задач мы используем равенство объемов одной фигуры, выраженные двумя различными способами.

Решим следующую задачу:

№3. Ребро AD пирамиды DABC  перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и АD, если .

Ответ: 2

При решении задач координатным методом расстояние от точки М до плоскости α  можно вычислить по формуле  ρ(М; α) = , где М(х0; у0; z0), а плоскость задана уравнением ax + by + cz + d = 0

Решим следующую задачу:

№4. В единичном кубе A…D1 найдите расстояние от точки А1 до плоскости ВDC1.

Решение.

Введем систему координат с началом в точке А , ось у пройдет по ребру АВ, ось х – по ребру АD, ось z – по ребру АА1. Тогда координаты  точек В (0; 1; 0) D (1; 0; 0;) C1(1; 1; 1) Составим уравнение плоскости, проходящей через точки  В, D, C1. 

 

Тогда – dx – dy + dz + d = 0     x + y – z – 1= 0.  Следовательно, ρ =

Ответ:

Следующий метод, который можно использовать при решении задач данного типа – метод опорных задач.

Применение данного метода состоит в применении известных опорных задач, которые формулируются как теоремы.

Решим следующую задачу:

№5. В единичном кубе   А…D1  найдите расстояние от точки D1 до плоскости АВ1С.

Рассмотрим применение векторного метода.

№6.  В единичном кубе   А…D1  найдите расстояние от точки А1 до плоскости ВDС1.

Итак, мы рассмотрели различные способы, которые можно использовать при решении данного типа задач. Выбор того или иного метода зависит от конкретной задачи и ваших предпочтений.

IV. Работа в группах

Попробуйте решить задачу разными способами.

№1. Ребро куба  А…D1 равно . Найдите расстояние от вершины С до плоскости BDC1.

№2. В правильном тетраэдре  АВСD с ребром  найдите расстояние от точки А до плоскости BDC

№3. В правильной треугольной призме АВСА1В1С1  все ребра которой равны 1, найдите расстояние от  А до плоскости ВСА1.

№4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от  А  до плоскости SCD.

V. Итог урока, домашнее задание, рефлексия

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Расстояние от точки до плоскости онлайн

С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку "Решить".

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Расстояние от точки до плоскости − теория, примеры и решения

Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:

Нахождение расстояния от точки до плоскости содержит следующие шаги:

  1. построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.
  2. нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
  3. вычисление расстояния между точками M0 и M1.

1. Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

Подставляя значение параметра t в выражения (4), находим проекцию M1(x1, y1, z1) точки M0 на плоскость (1).

3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:

Учитывая значение параметра t, имеем:

 

Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости

Решение.

Нормальный вектор плоскости имеет вид:

т.е. A=5, B=1, C=2.

Координаты точки M0: x0=2, y0=−1, z0=−9/31.

Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:

Из выражений (4) находим:

Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:

Вычислим расстояние между точками M0 и M1:

Упростим:

Ответ:

Расстояние от точки M0(2, -1, -9/31) до плоскости (7):

matworld.ru

Определение расстояния от точки до плоскости

Санкт-Петербургский государственный морской технический университет

Кафедра компьютерной графики и информационного обеспечения

ЗАНЯТИЕ 4

ПРАКТИЧЕСКОЕ ЗАДАНИЕ №4

Плоскость.

Определение расстояния от точки до плоскости.

1. Определение расстояния от точки до проецирующей плоскости.

Для того, чтобы найти действительную величину расстояния от точки до плоскости, необходимо:

·  из точки опустить перпендикуляр на плоскость;

·  найти точку пересечения проведенного перпендикуляра с плоскостью;

·  определить действительную величину отрезка, началом которого является заданная точка, а концом – найденная точка пересечения.

Плоскость может занимать в пространстве общее и частное положение. Под частным понимается положение, при котором плоскость перпендикулярна к плоскости проекций – такую плоскость называют проецирующей. Основной признак проецирующего положения: плоскость перпендикулярна к плоскости проекций, если она проходит через проецирующую прямую. В этом случае одна из проекций плоскости  прямая линия – ее называют следом плоскости.

Если плоскость проецирующая, то легко определить действительную величину расстояния от точки до плоскости. Покажем  это на примере определения расстояния от точки В до  фронтально-проецирующей плоскости, заданной следом Q2 на плоскости П2 (рис.1).

Плоскость Q перпендикулярна к фронтальной плоскости проекций, следовательно, любая к ней перпендикулярная линия будет параллельна к плоскости П2. А тогда прямой угол на плоскость П2 будет проецироваться без искажения, и можно из точки В2 провести перпендикуляр к следу Q2. Отрезок ВК находится в частном положении, при котором фронтальная проекция  В2К2 равна истинной величине искомого расстояния.

                               

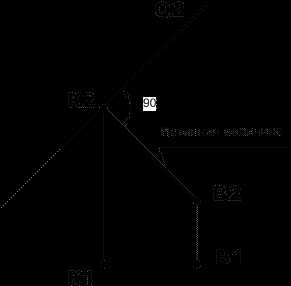
Рис.1. Определение расстояния от точки до проецирующей плоскости.

2.  Определение расстояния от точки до  плоскости общего положения.

Если плоскость занимает общее положение, то необходимо перевести ее в проецирующее положение. Для этого в ней проводится прямая частного положения (параллельная к одной из плоскостей проекций), которую можно перевести в проецирующее положение,  используя одно преобразование чертежа.

Прямая, параллельная плоскости П1, называется горизонталью плоскости и обозначается буквой h. Прямая, параллельная фронтальной плоскости проекций П2, называется фронталью плоскости и обозначается буквой f.Линии hиfназываются главными линиями плоскости. Решение задачи показано на следующем примере (рис.2).

Начальное условие: треугольник АВС задает плоскость. М - точка вне плоскости. Заданная плоскость занимает общее положение. Для перевода ее в проецирующее положение выполним следующие действия. Включить режим ОРТО (ORTHO), использовать команду Отрезок (Line) – провести любую горизонтальную линию, пересекающую фронтальную проекцию треугольника  А2В2С2 в двух точках. Проекция горизонтали, проходящей через эти точки,    обозначена h3.  Далее строится горизонтальная проекция h2.

Главная линия hможет быть преобразована в проецирующее положение, при котором заданная плоскость также станет проецирующей. Для этого необходимо повернуть горизонтальные проекции всех точек (вспомогательный четырехугольник АВСМ) в новое положение, при котором  линия h2 будет занимать вертикальное положение, перпендикулярное к оси Х. Удобно выполнить эти построения, используя плоскопараллельный перенос (копия проекции помещается на свободное место экрана).

В результате новая фронтальная проекция плоскости будет выглядеть в виде прямой линии (следа плоскости) А2*В2*.  Теперь из точки М2* можно провести перпендикуляр к следу плоскости. Новая фронтальная проекция М2*К2* = МК т.е. является искомым расстоянием от точки М до заданной плоскости АВС.

Далее необходимо построить проекции расстояния в начальном условии. Для этого из точки М1 проводится отрезок, перпендикулярный к линии h2, и на нем следует отложить от точки М1 отрезок, равный по величине М1*К1*. Чтобы построить фронтальную проекцию точки К2 из точки К1 проводится вертикальная линия связи, а из точки К2*  горизонтальная. Результат построений показан на рис.2.

                                 

ЗАДАНИЕ №4.  Найти истинную величину расстояния от точки М     до плоскости, заданной треугольником АВС. Ответ дать в мм.(таблица 1)

                                                                                 Таблица 1

Вариант

Точка А

Точка В

Х

Y

Z

X

Y

Z

1

140

10

30

105

10

50

2

150

25

65

75

40

80

3

160

30

15

120

60

50

4

80

90

30

60

10

10

5

20

50

40

50

30

70

6

35

55

25

95

20

35

7

70

40

50

20

75

40

8

15

65

35

35

20

65

9

100

10

50

60

80

90

Вариант

Точка С

Точка М

1

90

40

30

40

15

40

2

110

70

30

50

30

35

3

95

20

25

135

10

70

4

30

20

80

40

70

20

5

90

80

30

60

80

80

6

65

95

55

45

35

55

7

40

20

10

60

65

10

8

95

25

15

65

75

55

9

30

40

10

80

60

30

Проверка и зачет  выполненного ЗАДАНИЯ №4.

vunivere.ru