ГлавнаяРазноеНайти среднее квадратичное отклонение

Среднее квадратическое отклонение, методика расчета, применение. Найти среднее квадратичное отклонение


81. Среднее квадратическое отклонение, методика расчета, применение.

Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ - сигма). Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d2.

4. Перемножают квадраты отклонений на соответствующие частоты d2*p.

5. Находят сумму произведений ( d2*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

при n больше 30, или при n меньше либо равно 30, где n - число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

- 68,3% значений вариант находится в пределах М1

- 95,5% значений вариант находится в пределах М2

- 99,7% значений вариант находится в пределах М3

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

studfiles.net

Среднее квадратическое (квадратичное) отклонение

Для оценки рассеяния возможных значений слу­чайной величины вокруг ее среднего значения кроме дис­персии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной ве­личины X называют квадратный корень из дисперсии: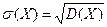

В тех случаях, когда жела­тельно, чтобы оценка рассеяния имела размерность слу­чайной величины, вычисляют среднее квадратическое от­клонение, а не дисперсию. Так, если X выражается в линейных метрах, то 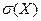будет выражаться также в линейных метрах, a D (X) - в квадратных метрах.

Задание 5-14..

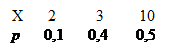1.Случайная величина X задана законом распределения

Найти среднее квадратическое отклонение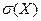

Решение. М(Х) = 2· 0, 1+3·0,4 + 10·0,5 = 6,4.

М(Х2) = 22· 0,1 + 32·0,4 + 102·0,5 = 54.

D(Х) = M(X2) - [M(Х)]2 = 54 - 6,42= 13,04.

Среднее квадратическое отклонение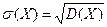

=3,61.

2. Известны дисперсии двух независимых случайных вели­чин: D(X) = 4, D(K)=3. Найти дисперсию суммы этих величин. Ответ: 7.

3.. Дисперсия случайной величины X равна 5. Найти дисперсию следующих величин:

а) X- 1; б) - 2Х; в) ЗХ + б. Ответ: а) 5; б) 20; в) 45.

4. Случайная величина X принимает только два значения: С и -С, каждое с вероятностью 0,5. Найти дисперсию этой величины.

Ответ: С2.

5. Найти дисперсию случайной величины, зная закон ее распре­деления

X 0,1 2 10 20

р 0,4 0,2 0,15 0,25 Ответ: 67,6404.

6. Случайная величина X может принимать два возможных зна­чения: х1с вероятностью 0,3 и х2с вероятностью 0,7, причем х2> х1. Найти х1 и x2зная, что М(Х)=2,7 и D (X) =0,21.

Ответ: х1= 2, х2= 3.

7. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: p1 = 0,3; р2 = 0,4; p3 = 0,5; p4 = 0,6. Найти математическое ожидание и дис­персию числа отказавших приборов. Ответ:1,8; 0,94.

8. Найти дисперсию случайной величины X - числа появлений события в 100 независимых испытаниях, в каждом вероят­ность наступления события равна 0,7. Ответ: 21.

9. Дисперсия случайной величины D(X) = 6,25. Найти среднее квадратическое отклонение а (X). Ответ: 2,5.

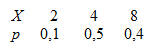10. Случайная величина задана законом распределения

Найти среднее квадратическое отклонение этой величины. Ответ: 2,2.

11. Дисперсия каждой из 9 одинаково распределенных взаимно независимых случайных величин равна 36. Найти дисперсию среднего арифметического этих величин. Ответ: 4.

12. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин. Ответ: 2,5.

 

Функция распределения ДСВ

Случайная дискретная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ задания не является общим: он неприменим, например, для случайных непрерывных величин.

Действительно, рассмотрим случайную величину X, возможные значения которой сплошь заполняют интервал (а, b). Можно ли составить перечень всех возможных значений X? Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность дать общий спо­соб задания любых типов случайных величин. С этой целью и вводят функции распределения вероятностей случайной величины.

Пусть x - действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее x, т. е. вероятность события X < х, обозначим через F(x). Разу­меется, если х изменяется, то, изменяется и F(x). Итак, F (x) - функция от х.

Функцией распределения называют функцию F(х), опре­деляющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, или

F(х)=P(X<x)

С геометрической точки зрения F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Иногда вместо термина "функция распределения" используют термин "интегральная функция".

Теперь можно дать более точное определение случайной непрерывной величины.

Случайную величину назы­вают непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с не­прерывной производной.



infopedia.su

Среднее квадратическое отклонение, методика расчета, применение — Мегаобучалка

Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ - сигма). Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d2.

4. Перемножают квадраты отклонений на соответствующие частоты d2*p.

5. Находят сумму произведений å( d2*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

при n больше 30,или при n меньше либо равно 30, где n - число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

- 68,3% значений вариант находится в пределах М±1s

- 95,5% значений вариант находится в пределах М±2s

- 99,7% значений вариант находится в пределах М±3s

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М±1s обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1s указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

megaobuchalka.ru

Среднеквадратическое отклонение — WiKi

Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок (измерений), это среднее арифметическое называют оценкой математического ожидания .

В литературе обычно обозначают греческой буквой σ{\displaystyle \sigma } (сигма) или буквой S{\displaystyle S}.

Основные сведения

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

Стандартное отклонение на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[1]):

S=1n∑i=1n(xi−x¯)2.{\displaystyle S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.} 

Стандартное отклонение на основании несмещённой оценки дисперсии (подправленная выборочная дисперсия[1], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):

S0=nn−1S2=1n−1∑i=1n(xi−x¯)2;{\displaystyle S_{0}={\sqrt {{\frac {n}{n-1}}S^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};} 

где S2{\displaystyle S^{2}}  — выборочная дисперсия; xi{\displaystyle x_{i}}  — i-й элемент выборки; n{\displaystyle n}  — объём выборки; x¯{\displaystyle {\bar {x}}}  — среднее арифметическое выборки (выборочное среднее):

x¯=1n∑i=1nxi=1n(x1+…+xn).{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).} 

Само по себе, однако, S0{\displaystyle S_{0}}  не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Обе оценки являются состоятельными[1].

В более общем случае среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[2]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии.

Правило трёх сигм

Правило трёх сигм (3σ{\displaystyle 3\sigma } ) — практически все значения нормально распределённой случайной величины лежат в интервале (x¯−3σ;x¯+3σ){\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x¯{\displaystyle {\bar {x}}}  истинная, а не полученная в результате обработки выборки).

Интерпретация величины среднеквадратического отклонения

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ=D[X]{\displaystyle \sigma ={\sqrt {D[X]}}}  отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

См. также

Примечания

  1. ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
  2. ↑ C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — DOI:10.1088/1674-1137/40/10/100001.

Литература

ru-wiki.org

Среднеквадратическое отклонение — википедия фото

Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок (измерений), это среднее арифметическое называют оценкой математического ожидания .

В литературе обычно обозначают греческой буквой σ{\displaystyle \sigma } (сигма) или буквой S{\displaystyle S}.

Основные сведения

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

Стандартное отклонение на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[1]):

S=1n∑i=1n(xi−x¯)2.{\displaystyle S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.} 

Стандартное отклонение на основании несмещённой оценки дисперсии (подправленная выборочная дисперсия[1], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):

S0=nn−1S2=1n−1∑i=1n(xi−x¯)2;{\displaystyle S_{0}={\sqrt {{\frac {n}{n-1}}S^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};} 

где S2{\displaystyle S^{2}}  — выборочная дисперсия; xi{\displaystyle x_{i}}  — i-й элемент выборки; n{\displaystyle n}  — объём выборки; x¯{\displaystyle {\bar {x}}}  — среднее арифметическое выборки (выборочное среднее):

x¯=1n∑i=1nxi=1n(x1+…+xn).{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).} 

Само по себе, однако, S0{\displaystyle S_{0}}  не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Обе оценки являются состоятельными[1].

В более общем случае среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[2]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии.

Правило трёх сигм

Правило трёх сигм (3σ{\displaystyle 3\sigma } ) — практически все значения нормально распределённой случайной величины лежат в интервале (x¯−3σ;x¯+3σ){\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x¯{\displaystyle {\bar {x}}}  истинная, а не полученная в результате обработки выборки).

Интерпретация величины среднеквадратического отклонения

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ=D[X]{\displaystyle \sigma ={\sqrt {D[X]}}}  отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

См. также

Примечания

  1. ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
  2. ↑ C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — DOI:10.1088/1674-1137/40/10/100001.

Литература

org-wikipediya.ru

Отклонение среднее квадратично относительное - Справочник химика 21

    Рассмотрим применение этой теории к расчету конкретных погрешностей химического анализа, причем будем решать только первую задачу. По степени отклонения от истинного результата погрешности делят на абсолютные, относительные и средние квадратичные (табл. 7,2). Абсолютные погрешности имеют знак, показывающий, в какую сторону отклоняются результаты от истинного (или среднего значения). За средний результат принимается среднее арифметическое х [c.130]     Для характеристики отклонений от среднего часто используют величину /называемую средним квадратичным отклонением величины X или флуктуацией. Относительную флуктуацию определяют как отношение среднего квадратичного отклонения к среднему значению данной случайной величины  [c.20]

    Важной характеристикой точности измерений является также относительная величина среднего квадратичного отклонения — коэффициент вариации  [c.276]

    Особенно важным является относительное среднее квадратичное отклонение ш А)  [c.334]

    Статистические характеристики случайных величин. Важнейшими характеристиками случайных величин являются дисперсия, средняя квадратичная ошибка (стандартное отклонение), коэффициент вариации, среднее значение. Дисперсия (а — для генеральной совокупности и — для выборки) — характеризует степень разброса полученных результатов относительно среднего значения резуль- [c.6]

    Точность расчета пределов воспламенения по аппроксимирующей формуле (6) характеризуется величиной б (6 — относительная ошибка рассчитанного значения, равная среднему квадратичному отклонению от экспериментального значения в долях единицы). [c.17]

    Доверительные интервалы для оценки математического ожидания, истинного значения измеряемой величины, среднего квадратичного отклонения. Оценка вероятности по относительной частоте Принцип максимального правдоподобия [c.153]

    Здесь S( u) — спектральная плотность случайного процесса. Интеграл, стоящий в числителе выражения (VII. 5), равен моменту инерции плоской фигуры, ограниченной кривой S((u) и осью абсцисс, относительно оси о) = О, а интеграл, стоящий в знаменателе, — площади фигуры. Квадратный корень из отношения этих интегралов является среднеквадратичным отклонением кривой S (аз) от оси m = 0 и характеризует, таким образом, среднюю квадратичную частоту соц изменения случайного процесса. Формула (VII. 5) справедлива для стационарных дифференцируемых случайных процессов с нормальным законом распределения значений ординат. [c.162]

    Задачи 7-11. Найти среднее квадратичное отклонение отдельного определения (S), относительное стандартное отклонение одного измерения в % (Sr), стандартное отклонение среднего арифметического (S-), относительное среднее квадратичное отклонение среднего арифметического (Sj ) в %, доверительный интервал при доверительной вероятности а) 0,95 б) 0,99. [c.9]

    Среднее квадратичное отклонение [7] при определении Кг составило не более 0,3 л моль , относительная погрешность результата при определении Н и Д8 — 2,3 кДж-моль и 1,2 Дж моль соответственно. [c.95]

    Расчет относительных мольных теплот растворения был выполнен в лаборатории автора одним методом в качестве неподвижных фаз были использованы жидкости одной и той же марки, но различных партий. Носители в указанных двух лабораториях различались, но тот и другой относились к наименее активным, силанизированным носителям. Внутрилабораторное среднее квадратичное отклонение относительного удерживания составляет 0,2%, среднее квадратичное отклонение относительной мольной теплоты растворения — 0,2 кДж/моль. [c.64]

    Шероховатость поверхности определяется [17] как совокупность неровностей с относительно малыми шагами, образующих рельеф поверхности и рассматриваемых в пределах участка, длина которого выбирается в зависимости от характера поверхности и равна базовой длине I . Как видно из этого определения, понятие шероховатость связано с базовой линией — длиной участка поверхности, выбираемой для определения шероховатости и позволяющей не учитывать неровности, шаг которых больше базовой длины. Непосредственное измерение микронеровностей и количественную оценку шероховатости проводят по виду профиля, т. е. по результатам рассмотрения сечения поверхности плоскостями, ориентированными в заданном направлении. Профиль характеризуют обычно с помощью средней линии, которая делит его так, что в пределах базовой длины сумма квадратов расстояний точек профиля до этой линии минимальна. Для количественной оценки шероховатости пользуются следующими параметрами среднее арифметическое отклонение профиля, среднее квадратичное отклонение профиля, высота неровностей, средняя высота неровностей, максимальная высота неровностей и др. [17, 56, 57, 59, 60]. В зависимости от числовых значений этих параметров шероховатость поверхностей подразделяют на 14 классов чистоты [17]. Средняя высота неровностей для первого класса чистоты составляет 20 мкм, наивысшему, 14 классу чистоты, соответствуют неровности высотой 0,06 мкм. [c.94]

    Если Ох Оф, то относительная ошибка определения сравнительно невелика. Однако с уменьшением величины Ох и ее приближением к величине Оф ошибка становится относительно большой вследствие колебаний значений Ох и Оф. Для повышения точности анализа выполняют несколько определений Ох+ф и Оф, вычисляют средние значения Б и находят среднее квадратичное отклонение а . Используя эту величину, можно представить [c.35]

    Т. е. Тгр — граничное показание шкалы пропускания, при котором кюветная ошибка равна инструментальной ошибке Ок — среднее квадратичное отклонение величины пропускания двух кювет относительно друг друга при смене в них одного и того же раствора. При пользовании одним и тем же прибором (постоянная чувствительность прибора), при одном и том же количестве единичных отсчетов и при одинаковой методике обработки кювет Тгр — постоянно. [c.236]

    Если эта величина мала, то равновесное значение величины А хорошо представляется величиной А, Если относительное среднее квадратичное отклонение не является малым (по сравнению с единицей), то А теряет свой физический смысл. [c.334]

    Рассмотрим следуюш ие две важные переменные. Для системы, которая может обмениваться энергией и частицами с резервуаром, мы получим выражение для относительного среднего квадратичного отклонения плотности (или концентрации ) NIV. [c.334]

    Относительное среднее квадратичное отклонение расчета по формуле составляет 9%. [c.307]

    В табл. 1 приведены также измеренные количества скандия, исправленные нри помощи наиболее точных данных относительно содержания железа, которые можно было получить. Эти данные (Ре") были получены посредством сравнения образцов и эталонов но счету в каналах Аж В. При этом согласие с истинными значениями получается вполне удовлетворительным и находится в пределах, задаваемых средним квадратичным отклонением. [c.148]

    Разброс параметров характеризуют а) предельным абсолютным значением б) предельным относительным значением в) средним квадратичным отклонением. [c.19]

    Разработаны и рекомендованы для дополнения ГОСТ 10398—63 на комплексонометрич. метод определения основного вещества в реактивах методики определения основного вещества в соединениях с относительной точностью, выражаемой средним квадратичным отклонением (8) из 10 определений 1п — 5= 0,04—0,1 (в зависимости от аниона соли) Ьа —5 = 0,04—0,06 2г—8 = 0 06—0,23 V—8 = = 0,15—0,21 5= 0,16 Оа—5= 0,15—0,21 8с—5 = = 0,1.....0,15% относительных. Табл, 1, библ. 19 назв [c.508]

    На примере химически чистой окиси и солей галлия показано, что по разработанному методу получены результаты определения с относительной точностью, характеризуемой средним квадратичным отклонением из 11 определений, равным 0,1%. Средний результат определений комплексонометрическим методом отличается от результата весового определения на —0,170- [c.85]

    Среднее арифметическое значение, Л Средняя квадратичная ошибка. Доверительная вероятность, а Коэффициент нормированных отклонений к Лбсолю1ная величина разности между Л И о 1а Относительная погрешность метода, I отн. [c.143]

    Как явствует из табл. 1, при определении 0,002 мкг. молибдена среднее квадратичное отклонение равно 25% (относительных).  [c.211]

    Например, при повторных взвешиваниях стеклянного фильтра были получены следующие результаты (в г) 10,2375 10,2374 10,2378 10,2375. Определить среднее арифметическое значение, дисперсию, среднюю квадратичную ошибку, среднюю квадратичную ошибку среднего арифметического, коэффициент нормирования отклонений, вероятное квадратичное отклонение среднего арифметического, истинную массу стеклянного фильтра и относительную ошибку взвешивания с надежностью а, равной 0,95. Для удобства вычислений запишем данные в виде таблицы  [c.302]

    Повторим еще раз, что совпадение 5 и 5с не является тривиальным. Первая величина является средним квадратичным отклонением, значение которого определяется рассеянием отдельных результатов относительно их среднего значения. Средняя квадратичная ошибка счета 5с является просто корнем квадратным из среднего значения. Эти два значения будут идентичными в рентгеновской эмиссионной спектроскопии, если процесс испускания квантов действительно случаен и результаты измерений не подвержены никаким другим ошибкам, кроме средней квадратичной ошибки счета. Мы попытаемся установить различие между 5 и 5с, всегда называя первую средним квадратичным отклонением, по уравнению (99), а последнюю — средней квадратичной ошибкой счета по уравнению (100). Необходимо отметить одно осложнение. Так как среднее значение N первоначально не устанавливается, обычно находят приближенное значение 5с извлечением квадратного корня из единственного значения N по уравнениям (94) и (98). Среднее квадратичное отклонение 5 можно рассчитать из уравнения (92) для любой экспериментальной величины. В частном случае в формулу (99) подставляются измеренные значения числа импульсов, но в качестве х в уравнении (92) могут быть также подставлены весовые проценты присутствующего элемента или какая-либо другая величина. [c.291]

    Совсем иное дело, если механизм изменчивости микробов мутационный. Тогда мутации возникали с течением времени за весь период роста каждой культуры. Вероятность мутации — малая величина поэтому число мутаций вначале было мало и, следовательно, статистические флюктуации были относительно велики. А затем каждая клетка, в том числе и мутировавшая, размножалась экспоненциально, и в результате образовывались миллионы резистентных клеток. Тем самым флюктуации числа мутантов также колоссально умножились. Качественно это легко понять. Пусть в какой-то интервал времени образовалось среднее число мутантов Av. До момента окончания роста культуры каждый из мутантов размножился в А, раз. Ясно, что в этом случае Var Av=Av, так как отдельные мутации независимы и подчинены закону Пуассона. Но мы измеряем на опыте дисперсию не мутаций, а чисел уже размножившихся резистентных клеток Ар== = A,Av. Среднее квадратичное отклонение Ар будет  [c.302]

    Средняя квадратичная погрешность (стандартное отклонение) характеризует разброс данных относительно среднего арифметического значения х определяемой величины  [c.37]

    Среднее квадратичное отклонение, характеризующее воспроизводимость прибора равно 5% (относительных). Средняя квадратичная ошибка метода 12% (относительных) включает как ошибку, связанную с приготовлением смеси, так и ошибку самого хроматографического анализа. Как видно иа [c.82]

    Предварительно, до введения проверки с помощью карт, на основании обработки достаточно большого материала находят величину средней квадратичной ошибки (сгр) или, лучше, коэффициент вариации (ур), характерный для результата анализа данного вида, выполняемого в соответствующих условиях. Затем периодически, например один раз в смену, анализируют (в шифрованном виде) одну или несколько контрольных проб с достаточно надежно установленным составом. Отклонения результатов анализа этих проб от паспортного содержания выражают для удобства в тех же единицах, что и параметр 0р или коэффициент вариации (в последнем случае — в процентах относительных). Эти величины с учетом знака откладывают по вертикальной оси. По горизонтальной оси откладывают порядковые номера илн даты контрольных определений. [c.65]

    Относительное среднее квадратичное отклонение расчета по фор.чуле составляет 13—16 /о. [c.308]

    Компонент Найдено 1 X, 0/ Стандартн. отклонение, Средняя квадратичн. ошибка - 0/ /0 Абсолютная ошибка % Результат анализа % Относительная ошибка . -.100, % [c.245]

    ПРИМЕРЫ РЕШЕН11Я ЗАДАЧ Пример 1. Найти среднее квадратичное отклонение отдельного определения (3), среднее квадратичное отклонение среднего арифметического (.5-), относительную среднюю квадратичную ошибку среднего арифметической ) в %, доверительный интервал для четырех [c.6]

    Для наховдения Рр достаточно знать xmin Для этого необходимо определить среднее значение разностей X = Т - и его среднее квадратичное отклонение . Принимая, что имеет некоторую величину отклонения от среднегозначвния постоянной и периодичес-IM чередующейся относительно в обе стороны, и зная фактические значения в конкретном климатическом районе за наблюдаемый период, определяем разности X = и находим X, и Х/т //  [c.72]

    Для типичных газов N имеет порядок ч исла Авогадро, так что относительное среднее квадратичное отклонение является беско. нечно малой величиной. Иногда этот результат рассматривают как доказательство эквивалентности канонического и микроканонического ансамблей, поскольку (5.252) указывает на то, что в каноническом ансамбле почти все системы обладают энергией Е. В более общем случае каноническое распределение пригодно когда ш ( )-большое каноническое распределение имеет место при ш Е) [c.336]

    Распад радиоактивного вещества — явление статистическое. Поэтому измеренное значение активности может несколько отличаться от истинного (среднего за большой промежуток времени) значения активности. Однако разброс результатов измерений лежит в нек-рых определенных пределах, к-рые могут быть на11дены с помощью методов теории вероятности. Для характеристики этих отклонении обычно используют среднюю квадратичную ошибку, определяемую соотношением D=У N, где IV — число зарегистрированных импульсов. Вероятность того, что действительная погрешность измерений будет меньше В, равна примерно 70%. Относительная ошибка, б = =1/l/ iV= l/увеличением числа зарегистрированных импу.тьсов. Таким образом, время измерения при заданно активности препарата определяется тем, с какой точностью необходимо произвести измерение активности препарата. [c.226]

    Наименьшее время измерения сигнала t зависит от скорости установления равновесного значения концентрации атомов элемента в пламени и от разрешаюшей способности регистрирующей схемы. Обычно оно составляет около 10 сек [4]. Под относительной чувствительностью понимают наименьшую концентрацию вещества в распыляемом растворе, при которой надежно обеспечивается наименьший регистрируемый аналитический сигнал. Относительную чувствительность принято выражать в весовых процентах, в частях на миллион (ррт) или в мкг1мл. Предельная чувствительность метода определяется чувствительностью регистрирующей схемы, а также погрешностями измерений. При оценке относительной чувствительности наименьший измеряемый сигнал иногда принимают равным пятикратному значению стандартного отклонения [7]. По мнению Львова [4], в качестве наименьшего аналитического сигнала можно считать сигнал, величина которого в 2 раза превышает среднюю квадратичную ошибку измерений  [c.208]

    Абсолютные величины характеризуют абсолютные зиачення показатс.тей, относительные — соотношение различных абсолютных показателей (темпы роста в процентах, удельный вес, коэффициенты, индексы). Средние величины выражают типичные свойства изучаемой совокупности качественно-однородных, но количественно не совпадаюп их друг с другом явлений (средняя заработная плата рабочих, средняя загрузка оборудования, средняя выработка). Наиболее распростране1И1ые виды средних — средняя арифметическая (простая и взвешенная) и средняя геометрическая. При отсутствии прямых данных о весах применяется средняя гармоническая. Используются также среднее линейное и среднее квадратичное отклонения, коэффициент вариации. [c.251]

    Определение кремния в различных объектах отличается лишь характером предварительной обработки анализируемого вещества. Метод применен к анализу черных сплавов, силикатов, руд, шлаков, огнеупорных материалов и т.д. /59-77/. Совершенно не мешает определению присутствие болыж количеств соляной, азотной, фосфорной кислот, хлористого калия, хлористого аммония, до I г хлоридов лития, бария, железа, кальция, бериллия, стронция, никеля, кобальта, марганца, цинка, хрома, олова, ртути, молибдата аммония. В присутствии Ю о-ного раствора хлористого кальция не мешают хлориды алюминия, титана и ванадила, цирко-нилсульфат, если их не более 0,5 г. Указанным методом был определен кремний в сотнях образцов пегматитов, в стекле, граните, гнейсах, амфиболитах, кварцево-слюдяСреднее квадратичное отклонений полученных результатов от данных весового анализа составляет + 0,24 относительных /77/. [c.11]

chem21.info

Среднеквадратическое отклонение — Википедия РУ

Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок (измерений), это среднее арифметическое называют оценкой математического ожидания .

В литературе обычно обозначают греческой буквой σ{\displaystyle \sigma } (сигма) или буквой S{\displaystyle S}.

Основные сведения

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

Стандартное отклонение на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[1]):

S=1n∑i=1n(xi−x¯)2.{\displaystyle S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.} 

Стандартное отклонение на основании несмещённой оценки дисперсии (подправленная выборочная дисперсия[1], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):

S0=nn−1S2=1n−1∑i=1n(xi−x¯)2;{\displaystyle S_{0}={\sqrt {{\frac {n}{n-1}}S^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};} 

где S2{\displaystyle S^{2}}  — выборочная дисперсия; xi{\displaystyle x_{i}}  — i-й элемент выборки; n{\displaystyle n}  — объём выборки; x¯{\displaystyle {\bar {x}}}  — среднее арифметическое выборки (выборочное среднее):

x¯=1n∑i=1nxi=1n(x1+…+xn).{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).} 

Само по себе, однако, S0{\displaystyle S_{0}}  не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Обе оценки являются состоятельными[1].

В более общем случае среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[2]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии.

Правило трёх сигм

Правило трёх сигм (3σ{\displaystyle 3\sigma } ) — практически все значения нормально распределённой случайной величины лежат в интервале (x¯−3σ;x¯+3σ){\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x¯{\displaystyle {\bar {x}}}  истинная, а не полученная в результате обработки выборки).

Интерпретация величины среднеквадратического отклонения

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ=D[X]{\displaystyle \sigma ={\sqrt {D[X]}}}  отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

См. также

Примечания

  1. ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
  2. ↑ C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — DOI:10.1088/1674-1137/40/10/100001.

Литература

http-wikipediya.ru