Как найти НОК (наименьшее общее кратное). Нок как узнать
Найти наименьшее общее кратное (НОК)
Наименьшее общее кратное для двух целых чисел - это наименьшее из всех целых чисел, которое делится нацело и без остатка на оба заданных числа.
Способ 1. Найти НОК можно, по очереди, для каждого из заданных чисел, выписывая в порядке возрастания все числа, которые получаются путем их умножения на 1, 2, 3, 4 и так далее.
Пример для чисел 6 и 9. Умножаем число 6, последовательно, на 1, 2, 3, 4, 5. Получаем: 6, 12, 18, 24, 30 Умножаем число 9, последовательно, на 1, 2, 3, 4, 5. Получаем: 9, 18, 27, 36, 45 Как видно, НОК для чисел 6 и 9 будет равно 18.
Данный способ удобен, когда оба числа небольшие и их несложно умножать на последовательность целых чисел. Однако, бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также, когда исходных чисел три или даже больше.
Способ 2. Найти НОК можно, разложив исходные числа на простые множители. После разложения необходимо вычеркнуть из получившихся рядов простых множителей одинаковые числа. Оставшиеся числа первого числа будут множителем для второго, а оставшиеся числа второго - множителем для первого.
Пример для числе 75 и 60. Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5. Как видно, множители 3 и 5 встречаются в обоих строках. Мысленно их "зачеркиваем". Выпишем оставшиеся множители, входящие в разложение каждого из этих чисел. При разложении числа 75 у нас осталось число 5, а при разложении числа 60 - остались 2 * 2 Значит, чтобы определить НОК для чисел 75 и 60, нам нужно оставшиеся числа от разложения 75 (это 5) умножить на 60, а числа, оставшиеся от разложения числа 60 (это 2 * 2 ) умножить на 75. То есть, для простоты понимания, мы говорим, что умножаем "накрест". 75 * 2 * 2 = 300 60 * 5 = 300 Таким образом мы и нашли НОК для чисел 60 и 75. Это - число 300.
Пример. Определить НОК для чисел 12, 16, 24 В данном случае, наши действия будут несколько сложнее. Но, сначала, как всегда, разложим все числа на простые множители 12 = 2 * 2 * 3 16 = 2 * 2 * 2 * 2 24 = 2 * 2 * 2 * 3 Чтобы правильно определить НОК, выбираем наименьшее из всех чисел (это число 12) и последовательно проходим по его множителям, вычеркивая их, если хотя бы в одном из других рядов чисел встретился такой же, еще не зачеркнутый множитель.
Шаг 1 . Мы видим, что 2 * 2 встречаются во всех рядах чисел. Зачеркиваем их. 12 = 2 * 2 * 3 16 = 2 * 2 * 2 * 2 24 = 2 * 2 * 2 * 3
Шаг 2. В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается. 12 = 2 * 2 * 3 16 = 2 * 2 * 2 * 2 24 = 2 * 2 * 2 * 3
Как видим, при разложении числа 12 мы "вычеркнули" все числа. Значит нахождение НОК завершено. Осталось только вычислить его значение. Для числа 12 берем оставшиеся множители у числа 16 (ближайшего по возрастанию) 12 * 2 * 2 = 48 Это и есть НОК
Как видим, в данном случае, нахождение НОК было несколько сложнее, но когда нужно его найти для трех и более чисел, данный способ позволяет сделать это быстрее. Впрочем, оба способа нахождения НОК являются правильными.
profmeter.com.ua
Как найти НОК?
Как найти НОК?

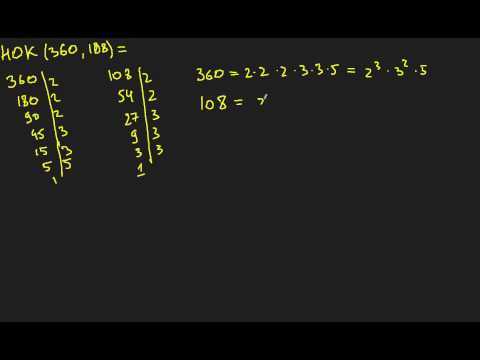
Для многих учеников математика – один из самых проблемных предметов. Хотя на самом деле это очень интересная, хоть и непростая наука. В ней главное не только заучить, но и понять выученное. Сегодня мы предлагаем вам разобраться в вопросе, как найти НОК чисел.
Понятие НОК
Вначале необходимо разобраться, что такое кратное. Кратным называется число, которое делится на данное число полностью, т.е. без остатка. Например, для 4 кратными числами будут 4, 8, 16 и т. д. Общим кратным называется число, на которое делится на каждое из данных чисел без остатка. Если взять числа 8 и 16, то их общие кратные - 16, 32, 48, 64 и т. д.
Наименьшим общим кратным, или НОК, нескольких чисел называют наименьшее натуральное число, которое само можно поделить на каждое из данных чисел без остатка. Для уже рассмотренных 8 и 16 это число 16.
Решение задач
Для того чтобы найти НОК двух чисел, сделайте следующее:
Разложите данные в задаче числа на простые множители, т.е. простые числа (они только делятся на единицу и на само себя), которые при перемножении дают исходное. Для этого разделите лист вертикальной чертой. В первом столбике запишите данное число, а во втором - самый маленький общий делитель. Частное этих чисел записываете в первый столбик. И таким образом делите число, пока не получите единицу.
Допустим, требуется найти НОК 21 и 48. Разложим их:
| 21|3 | 48|2 |
| 7|7 | 24|2 |
| 1| | 12|2 |
elhow.ru
НОД и НОК чисел с решением | Наибольший общий делитель и наименьшее общее кратное нескольких чисел
Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найти НОД и НОК
Найдено НОД и НОК: 2417
Как пользоваться калькулятором
- Введите числа в поле для ввода
- В случае ввода некорректных символов поле для ввода будет подсвечено красным
- нажмите кнопку "Найти НОД и НОК"
Как вводить числа
- Числа вводятся через пробел, точку или запятую
- Длина вводимых чисел не ограничена, так что найти НОД и НОК длинных чисел не составит никакого труда
Что такое НОД и НОК?
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД.Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК.
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
1. Признак делимости числа на 2Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.Пример: определить, делится ли на 2 число 34938.Решение: смотрим на последнюю цифру: 8 - значит число делится на два.
2. Признак делимости числа на 3Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.Пример: определить, делится ли число 34938 на 3.Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
3. Признак делимости числа на 5Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.Пример: определить, делится ли число 34938 на 5.Решение: смотрим на последнюю цифру: 8 - значит число НЕ делится на пять.
4. Признак делимости числа на 9Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.Пример: определить, делится ли число 34938 на 9.Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36):
- Раскладываем оба числа на множители: 28 = 1·2·2·7, 36 = 1·2·2·3·3
- Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.
- Вычисляем произведение этих множителей: 1·2·2 = 4 - это и есть наибольший общий делитель чисел 28 и 36.
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
- Находим произведение чисел 28 и 36: 28·36 = 1008
- НОД(28, 36), как уже известно, равен 4
- НОК(28, 36) = 1008 / 4 = 252.
Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c).
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример: найти НОД и НОК для чисел 12, 32 и 36.
- Cперва разложим числа на множители: 12 = 1·2·2·3, 32 = 1·2·2·2·2·2, 36 = 1·2·2·3·3.
- Найдём обшие множители: 1, 2 и 2.
- Их произведение даст НОД: 1·2·2 = 4
- Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96.
- Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3, 36 = 1·2·2·3·3, НОД = 1·2·2·3 = 12.
- НОК(12, 32, 36) = 96·36 / 12 = 288.
programforyou.ru
как узнать НОД и НОК числа
Наибольший общий делитель Общий делитель. Наибольший общий делитель. Общим делителем нескольких чисел называется число, которое является делите-лем каждого из них. Например, числа 36, 60, 42 имеют общие делители 2, 3 и 6. Среди всех общих делителей всегда есть наибольший, в данном случае это 6. Это и есть наибольший общий делитель (НОД) . Чтобы найти наибольший общий делитель (НОД) нескольких чисел надо: 1) представить каждое число как произведение его простых множителей, например: 360 = 2 · 2 · 2 · 3 · 3 · 5 , 2) записать степени всех простых множителей: 360 = 2 · 2 · 2 · 3 · 3 · 5 = 23 · 32 · 51, 3) выписать все общие делители (множители) этих чисел; 4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях; 5) перемножить эти степени. П р и м е р . Найти НОД чисел: 168, 180 и 3024. Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 23 · 31 · 71 , 180 = 2 · 2 · 3 · 3 · 5 = 22 · 32 · 51 , 3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 24 · 33 · 71 . Выпишем наименьшие степени общих делителей 2 и 3 и перемножим их: НОД = 22 · 31 = 12 . <a rel="nofollow" href="http://www.bymath.net/studyguide/ari/ari8.html" target="_blank">http://www.bymath.net/studyguide/ari/ari8.html</a> Наименьшее общее кратное Общее кратное. Наименьшее общее кратное. Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные. Среди всех общих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК) . Чтобы найти наименьшее общее кратное (НОК) нескольких чисел надо: 1) представить каждое число как произведение его простых множителей, например: 504 = 2 · 2 · 2 · 3 · 3 · 7 , 2) записать степени всех простых множителей: 504 = 2 · 2 · 2 · 3 · 3 · 7 = 23 · 32 · 71, 3) выписать все простые делители (множители) каждого из этих чисел; 4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел; 5) перемножить эти степени. П р и м е р . Найти НОК чисел: 168, 180 и 3024. Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 23 · 31 · 71 , 180 = 2 · 2 · 3 · 3 · 5 = 22 · 32 · 51 , 3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 24 · 33 · 71 . Выписываем наибольшие степени всех простых делителей и перемножаем их: НОК = 24 · 33 · 51 · 71 = 15120 . <a rel="nofollow" href="http://www.bymath.net/studyguide/ari/ari9.html" target="_blank">http://www.bymath.net/studyguide/ari/ari9.html</a>
чего проще посмотреть в вике. писать много.
нод замечательно считается алгоримом Евклида пишешь их рядом и раз за разом вычитаешь из большего меньшее, пока не получится ноль например: 35 56 35 21 14 21 14 7 7 7 0 7 НОД (35, 56) = 7. ну а НОК (а, b) = a*b/HOD(a,b) например, НОК (35, 56) = 35*56/ HOD(35, 56) = 35*56/ 7 = 280
touch.otvet.mail.ru
Как находить НОК и НОД?
чтобы найти НОД надо: 1) разложить их на простые множители 2)из множителей, входящих в разложение одного из чисел вычеркнуть те, которые не входят в разложение других чисел 3) найти произведение оставшихся множителей Пример: 12 и 32 раскладываем: 12:2=6:2=3:3=1 32:2=16:2=8:2=4:2=2:2=1 12 = 2 * 2 * 3 32 = 2* 2 * 2 * 2 * 2 Вычеркиваем 3 и 12 и три двойки из 32 НОД (12; 32) = 2 * 2 = 4 Чтобы найти НОК надо: 1)разложить их на простые множители 2) выписать множители входящие в разложение одного из чисел 3) добавить к ним недостающие множители из разложений остальных чисел 4)найти произведение получившихся множителей Пример: 20 и 11 20:2=10:2=5:5=1 11 - простое число делится само на себя. НОК (20; 11) = 2*2*5 * 11 = 220.
пример 278 и 608 👍
ваще на изи зянскую
Нод — это наибольший общий делитель. Нок — это наименьшее общее кратное
чтобы найти НОД надо: 1) разложить их на простые множители 2)из множителей, входящих в разложение одного из чисел вычеркнуть те, которые не входят в разложение других чисел 3) найти произведение оставшихся множителей Чтобы найти НОК надо: 1)разложить их на простые множители 2) выписать множители входящие в разложение одного из чисел 3) добавить к ним недостающие множители из разложений остальных чисел 4)найти произведение получившихся множителей
чтобы найти НОД надо: 1) разложить их на простые множители 2)из множителей, входящих в разложение одного из чисел вычеркнуть те, которые не входят в разложение других чисел 3) найти произведение оставшихся множителей Чтобы найти НОК надо: 1)разложить их на простые множители 2) выписать множители входящие в разложение одного из чисел 3) добавить к ним недостающие множители из разложений остальных чисел 4)найти произведение получившихся множителей
Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК). Кратное числу «a» — это число, которое само делится на число «a» без остатка. Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 … Кратные 9: 18, 27, 36, 45 … Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество. кратные и делители числа Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
1) разложить их на простые множители 2)из множителей, входящих в разложение одного из чисел вычеркнуть те, которые не входят в разложение других чисел 3) найти произведение оставшихся множителей Пример: 12 и 32 раскладываем: 12:2=6:2=3:3=1 32:2=16:2=8:2=4:2=2:2=1 12 = 2 * 2 * 3 32 = 2* 2 * 2 * 2 * 2 Вычеркиваем 3 и 12 и три двойки из 32 НОД (12; 32) = 2 * 2 = 4 Чтобы найти НОК надо: 1)разложить их на простые множители 2) выписать множители входящие в разложение одного из чисел 3) добавить к ним недостающие множители из разложений остальных чисел 4)найти произведение получившихся множителей Пример: 20 и 11 20:2=10:2=5:5=1 11 - простое число делится само на себя. НОК (20; 11) = 2*2*5 * 11 = 220.
разложить их на простые множители выписать множители входящие в разложение одного из чисел добавить к ним недостающие множители из разложений остальных чисел найти произведение получившихся множителей
touch.otvet.mail.ru
Как найти НОК трех чисел?
Geve, ГУГЛ? ЯНДЕКС? Вот переходим <a rel="nofollow" href="http://umal.me/0qc" target="_blank">сюда</a>
Девочки на ночь! <a rel="nofollow" href="http://wbt.link/4N6cy" target="_blank"> Снять девочку! ЖМИ!!</a>
Geve, Розыгрыш iPhone 7. Выиграй его сегодня !! Заходи на <a rel="nofollow" href="http://umal.me/0rv" target="_blank">этот сайт</a>. Никаких предоплат и смс!
Здравствуйте. Пришлите мне свое задание на почту: [email protected] А то здесь писать не очень удобно. Нами уже приблизительно 2027 задач сделано!
Загрузите свое задание на сайт: <a rel="nofollow" href="http://umal.me/0ps" target="_blank" >Онлайн-решебник</a> Или пришлите мне на мейл: [email protected] А то здесь писать не очень удобно. Мы уже решили 1715 заданий!
так же, как и двух
Наименьшим общим кратным данных натуральных чисел называют наименьшее натуральное число, кратное каждому из данных чисел. Пример. НОК (24, 42)=168. Это самое маленькое число, которое делится и на 24 и на 42. Для нахождения НОК нескольких данных натуральных чисел надо: 1) разложить каждое из данных чисел на простые множители; 2) выписать разложение большего из чисел и умножить его на недостающие множители из разложений других чисел. Наименьшее кратное двух взаимно простых чисел равно произведению этих чисел. Пример 1. Найти НОК (35; 40). Разложим числа 35 и 40 на простые множители. 35=5∙7, 40=2∙2∙2∙5 или 40=23∙5 Берем разложение большего числа 40 и дополняем его недостающими множителями. НОК (35; 40)=23∙5∙7=40∙7=280. Ответ: НОК (35; 40)=280. Пример 3. Найти НОК (75; 120; 150). Разложим числа 75, 120 и 150 на простые множители. 75=3∙52, 120=23∙3∙5, 150=2∙3∙52 Возьмем разложение большего числа 150 и дополним его двумя «двойками», так как в разложении числа 120 имеется три «двойки», а в разложении числа 150 – только одна. НОК (75; 120; 150)=2∙3∙52∙2∙2=150∙4=600. Ответ: НОК (75; 120; 150)=600. Вывод: при нахождении НОК выписывают произведение всех простых (различных) множителей, имеющихся в разложении этих чисел, причем, каждый из множителей берется с наибольшим из имеющихся показателей степеней.
touch.otvet.mail.ru
Как находить НОК и НОД?
Чтобы сократить записи придумали, что кратно будут записывать так: , а делит так: Каждое число является делителем других чисел, которые называются кратными этому числу. К (22) = Изобразим множества делителей чисел 18, 24 Д (18) Д (24)={2; 3; 6} Наибольший из общих делителей – 6, НОД (18; 24)=6 Изобразим множества кратных числам 18 и 22 К (18) К (24)={72; 144; …} – общие кратные 18 и 22 Наименьшее из общих кратных – 72. НОК (18; 24)= 72 Как находить НОД и НОК? Для чисел 18 и 24 это просто: - чтобы найти НОД перебираем общие делители 2; 3, пока не находим наибольший -6. - чтобы найти НОК умножаем 18 на 2, на 3 и так далее, пока не найдем число, которое делится на 24 – это 72 Если же числа большие, то их раскладывают на простые множители 600 2 300 2 150 2 75 3 25 5 5 5 1 108 2 54 2 27 3 9 3 3 3 1 НОД должен содержать все общие множители в наименьшей степени (подчеркнуты) : НОД (600; 108)= НОК должен содержать все множители в наибольшей степени (жирный шрифт) : НОК (600;108) = =5400 НОД (27;14)=1, так как у них нет общих делителей, кроме 1. 27=33, а Такие числа называют взаимно простыми НОК (27;14)= по той же самой причине, у них нет общих делителей. Как всегда, новые открытия стали сразу применяться. Удобно использовать методы нахождения НОК при сложении дробей. Наименьший общий знаменатель – это и есть НОК знаменателей. . НОД (408;90) 1 НО4 (408; 90) = 2040 НОД (92; 51)=1– взаимно простые НОК (92;51)=92*51= 4692
<a rel="nofollow" href="http://interneturok.ru/ru/school/matematika/6-klass" target="_blank" >http://interneturok.ru/ru/school/matematika/6-klass</a>
Находим НОК - наибольшее общее кратное, возьмем 2 числа - 10 и 15 Сначала находим НОК числа 10, делем на самое наименьшее число, если к примеру 10 делиться еще и на 5 то делим на 2 т. к. 2 самое маленькое число на которое можно делать (а делить можно на 2, 3, 5, 7,11,13 и так далее) Видим что число 10 делиться на 2, будет 5 и 5 = 1. 10|2 5|5 1| Находим НОК числа 15 Видим что число на самое маленькое делиться на 3, будет 5 и 5 =1 15|3 5|5 1| Смотрим числа на которые мы делили, и если видим одинаковые обводим их в кружок. остальные числа складывает 2+3 =5 Мы нашли НОК
хотите всё знать заходите на сайт готдомзад
Пример: 12 и 15 НОК=60 12 и 15 НОД=3
Нод — это наибольший общий делитель. Нок — это наименьшее общее кратное
ример: 12 и 15 НОК=60 12 и 15 НОД=3
чтобы найти НОД надо: 1) разложить их на простые множители 2)из множителей, входящих в разложение одного из чисел вычеркнуть те, которые не входят в разложение других чисел 3) найти произведение оставшихся множителей Чтобы найти НОК надо: 1)разложить их на простые множители 2) выписать множители входящие в разложение одного из чисел 3) добавить к ним недостающие множители из разложений остальных чисел 4)найти произведение получившихся множителей
touch.otvet.mail.ru











