Как найти область допустимых значений. Одз как искать
Область допустимых значений
Область допустимых значений алгебраического выражения (сокращенно ОДЗ) - это множество значений переменной, при которых это выражение определено.
В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:
1. ОДЗ:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
2. ОДЗ:
Выражение, стоящее в знаменателе дроби, не может быть равно нулю.
3. ОДЗ:
Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
4. , ОДЗ:
5. Есть две функции, которые содержат "скрытую" дробь:
и
6. ОДЗ:
Степень корня - натуральное число, отличное от 1.
Таким образом, функции и имеют разную область определения.
Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь "снаружи" "внутрь".
Поясню на примере:
Найти область определения функции:
Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции
Я специально выбрала "страшную", на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.
"Просканируем" выражение, стоящее в правой части равенства:
1. Мы видим дробь:
Знаменатель дроби не равен нулю. Записываем:
2. Мы видим в знаменателе логарифм:
Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
Записываем:
3.Мы видим квадратный корень:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
Записываем:
Теперь запишем все ограничения в систему неравенств:
Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:
И.В. Фельдман, репетитор по математике
ege-ok.ru
Находить ли ОДЗ?
Разделы: Математика
В уравнениях и неравенствах вида , , , , пересечение областей определения функций и называют областью допустимых значений (ОДЗ) переменной, а также ОДЗ уравнения или неравенства соответственно.
При решении уравнений (неравенств) с одной переменной, когда встает вопрос – находить ли ОДЗ, часто можно услышать категоричное «да» и не менее категоричное «нет». «Сначала нужно найти ОДЗ, а затем приступать к решению уравнения (неравенства)», - утверждают одни. «Незачем тратить время на ОДЗ, по ходу решения будем переходить к равносильному уравнению (неравенству) или к равносильной системе уравнений и неравенств или только неравенств. В конце концов, если это уравнение, то можно сделать проверку», - утверждают другие.
Так находить ли ОДЗ?
Конечно, однозначного ответа на этот вопрос не существует. Нахождение ОДЗ уравнения или неравенства не является обязательным элементом решения. В каждом конкретном примере этот вопрос решается индивидуально.
В одних случаях нахождение ОДЗ упрощает решение уравнения или неравенства (примеры 1-5), а в ряде случаев даже является необходимым этапом решения (примеры 1, 2, 4).
В других случаях (примеры 6, 7) от предварительного нахождения ОДЗ стоит отказаться, так как оно делает решение более громоздким.
Пример 1. Решить уравнение .
Решение.
Возведение обеих частей уравнения в квадрат не упростит, а усложнит его и не позволит избавиться от радикалов. Нужно искать другой способ решения.
Найдем ОДЗ уравнения:
Ответ: 4.
Пример 2. Решить уравнение .
Решение.
Наличие в уравнении радикалов различных степеней – второй, третьей и шестой – делает решение сложным. Поэтому, прежде всего, найдем ОДЗ уравнения:
Непосредственной подстановкой убеждаемся, что является корнем исходного уравнения.
Ответ: 2.
Пример 3. Решить неравенство .
Решение.
Конечно, можно решать это неравенство, рассматривая случаи: , , но нахождение ОДЗ сразу же упрощает это решение.
ОДЗ:
Подставляя это единственное значение в исходное неравенство, получим ложное числовое неравенство . Следовательно, исходное неравенство не имеет решения.
Ответ: нет решения.
Пример 4. Решить уравнение .
Решение.
Запишем уравнение в виде .
Уравнение вида равносильно смешанной системе т.е.
Конечно, здесь нахождение ОДЗ излишне.
В нашем случае получим равносильную систему т.е.
Уравнение равносильно совокупности Уравнение рациональных корней не имеет, но оно может иметь иррациональные корни, нахождение которых вызовет у учащихся затруднения. Поэтому поищем другой способ решения.
Вернемся к первоначальному уравнению, запишем его в виде .
Найдем ОДЗ: .
При правая часть уравнения , а левая часть . Следовательно, исходное уравнение в области допустимых значений переменной х равносильно системе уравнений решением которой является только одно значение .
Таким образом, в данном примере именно нахождение ОДЗ позволило решить исходное уравнение.
Ответ: 0.
Пример 5. Решить уравнение .
Решение.
Так как , а , то при решении исходного уравнения нужно будет избавляться от модулей (раскрывать их).
Поэтому, сначала имеет смысл найти ОДЗ уравнения:
Итак, ОДЗ:
Упростим исходное уравнение, воспользовавшись свойствами логарифмов.
,
,
.
Так как в области допустимых значений переменной х и , то , а , тогда получим равносильное уравнение:
,
.
Учитывая, что в ОДЗ , перейдем к равносильному уравнению и решим его, разделив обе части на 3.
Ответ: − 4,75.
Замечание.
Если не находить ОДЗ, то при решении уравнения необходимо было бы рассмотреть четыре случая: , , , . На каждом из этих промежутков знакопостоянства выражений, стоящих под знаком модуля, нужно было бы раскрыть модули и решить полученное уравнение. Кроме того еще и выполнить проверку. Мы видим, что нахождение ОДЗ исходного уравнения значительно упрощает его решение.
При решении следующих примеров предварительно ОДЗ находить не будем, так как это сделает решение более громоздким.
Пример 6. Решить неравенство .
Решение.
Исходное неравенство запишем в виде . Учитывая, что функция непрерывна и убывающая при , перейдем к равносильной системе неравенств:
Решением последнего неравенства, а, значит, и исходного является множество .
Ответ: .
Замечание. Если бы мы находили ОДЗ, то нужно было бы решать систему неравенств Все эти неравенства вошли в рассматриваемую при решении систему неравенств, причем, в процессе преобразования этой системы, все неравенства, из которых и состоит ОДЗ, оказались лишними. Таким образом, в данном примере нахождение ОДЗ только сделало бы решение более громоздким.
Пример 7. Решить неравенство .
Решение.
Так как переменная х входит и в основание логарифма, то при решении этого неравенства необходимо будет рассмотреть два случая: и . Поэтому отдельно находить ОДЗ нецелесообразно.
Итак, представим исходное неравенство в виде и оно будет равносильно совокупности двух систем:
Ответ: .
xn--i1abbnckbmcl9fb.xn--p1ai
ОДЗ | Алгебра
Найти ОДЗ — область допустимых значений — задание, которое в алгебре встречается как в виде самостоятельных примеров, так и при решении уравнений, неравенств и их систем.
ОДЗ многочлена — любое значение переменной.
Дробь имеет смысл, если знаменатель отличен от нуля.
Следовательно, ОДЗ дроби — все значения переменной, за исключением тех, в которых знаменатель обращается в нуль.
Выражение, стоящее под знаком корня чётной степени (в том числе, под знаком квадратного корня), должно быть неотрицательным.
Следовательно, ОДЗ выражения, содержащего переменную под знаком корня чётной степени — все значения переменной, при которых это выражение больше либо равно нуля.
Выражение, стоящее под знаком корня чётной степени (в том числе, под знаком квадратного корня) в знаменателе дроби, должно быть положительным.
То есть ОДЗ выражения с корнем чётной степени в знаменателе — множество значений переменной, при котором это выражение строго больше нуля.
Выражение, стоящее под знаком логарифма, должно быть положительным.
Выражение, стоящее в основании логарифма, должно быть положительным и не равным единице.
Выражение, стоящее под знаком синуса, может принимать любые значения (ОДЗ синуса — любые значения переменной).
Выражение, стоящее под знаком косинуса, может принимать любые значения (ОДЗ косинуса — любые значения переменной).
ОДЗ тангенса можно рассматривать как ОДЗ дроби
ОДЗ котангенса находим как ОДЗ дроби
Выражение, стоящее под знаком арксинуса, должно быть не меньшим -1 и не большим 1 (то есть ОДЗ арксинуса — промежуток [-1;1]).
Выражение, стоящее под знаком арккосинуса, должно быть не меньшим -1 и не большим 1 (ОДЗ арккосинуса — промежуток [-1;1]).
Выражение, стоящее под знаком арктангенса, может принимать любые значения (ОДЗ арктангенса — любые значения f(x)).
Выражение, стоящее под знаком арккотангенса, может принимать любые значения (ОДЗ арккотангенса — любые значения f(x)).
Выражение, стоящее в показателе степени, основание которой — положительное число, может принимать любые значения.
В ходе изучения темы «Степенная функция» обобщается информация по области допустимых значений степени и корня.
- Если α — натуральное число, то f(x)∈R.
- Если α — целое отрицательное число или нуль, то f(x)≠0.
- Если α — нецелое положительное число, то то f(x)≥0.
- Если α — нецелое отрицательное число, то то f(x)>0.
www.algebraclass.ru
Как найти область допустимых значений
Область допустимых значений функции нельзя путать с областью значений функции. Если первое – это все х, при которых уравнение или неравенство может быть решено, то второе – все значения функции, то есть у. Об области допустимых значений нужно помнить всегда, поскольку нередко найденные значения х коварно оказываются вне этой совокупности и поэтому не могут быть решением уравнения.Вам понадобится
- - уравнение или неравенство с переменной.
Инструкция
- Изначально в качестве области допустимых значений возьмите бесконечность. То есть представьте, что уравнение можно решить при всех х. После этого, используя несколько несложных запретов математики (нельзя делить на ноль, выражения под корнем четной степени и логарифма должно быть больше нуля), исключайте из ОДЗ недопустимые значения переменной.
- Если переменная х заключена в выражении под корень четной степени, поставьте условие: выражение под корнем должны быть меньше нуля. Затем решите это неравенство, найденный интервал исключите из области допустимых значений. Обратите внимание, не надо решать все уравнение – при поиске ОДЗ вы решаете лишь его небольшой кусочек.
- Обратите внимание на знак деления. Если в выражении есть знаменатель, содержащий переменную, приравняйте его к нулю и решите полученное уравнение. Исключите полученные значения переменной из области допустимых значений.
- Если в выражении есть знак логарифма с переменной в основании, обязательно поставьте следующее ограничение: основание всегда должно быть больше нуля и не равно единице. Если же переменная стоит под знаком логарифма, укажите, что все выражение в скобках должно быть больше единицы. Решите полученные небольшие уравнения и исключите недопустимые значения из ОДЗ.
- Если в уравнении или неравенстве несколько корней четной степени, операций деления или логарифмов, найдите недопустимые значений отдельно для каждого выражения. Затем объедините решение, вычитая все полученные результаты из области допустимых значений.
- Даже если вы нашли ОДЗ и полученные при решении уравнения корни удовлетворяют ему, это не всегда значит, что эти значения х являются решением, поэтому всегда проверяйте правильность решения подстановкой. Например, попробуйте решить следующее уравнение: √ (2х-1)=-х. В область допустимых значений здесь войдут все числа, удовлетворяющие 2х-1≥0, то есть х≥1/2. Для решения уравнения возведите обе части в квадрат, после упрощений у вас получится один корень х=1. Обратите внимание, этот корень входит в ОДЗ, но при подстановке вы убедитесь, что он не является решением уравнения. Окончательный ответ – корней нет.
completerepair.ru
ОДЗ. Зачем, когда и как?
ОДЗ. Зачем, когда и как?
Шамшурин А.В. 11Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №31»
Гагарина Н.А. 11Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №31»
Текст работы размещён без изображений и формул.Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Введение
Я начал работу с того, что в Интернете пересмотрел множество тем по математике и выбрал эту тему, потому что уверен, что важность нахождения ОДЗ играет огромную роль в решении уравнений и задач. В своей исследовательской работе я рассмотрел уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для меня хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ. Это и подтолкнуло меня к исследованию темы, целью которой, стало показать, что овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ. Чтобы достичь этой цели, я исследовал дополнительную литературу и другие источники. Мне стало интересно, а знают учащиеся нашей школы: когда, зачем и как находить ОДЗ. Поэтому я провёл тест по теме «Когда, зачем и как находить ОДЗ?» (было дано 10 уравнений). Количество учащихся – 28. Справились – 14 %, опасность ОДЗ (учли) – 68 %, необязательность (учли) – 36 %.
Цель: выявление: когда, зачем и как находить ОДЗ.
Проблема: уравнения и неравенства, в которых нужно находить ОДЗ, не нашли места в курсе алгебры систематического изложения, возможно поэтому я и мои сверстники часто делаем ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об ОДЗ.
Задачи:
- Показать значимость ОДЗ при решении уравнений и неравенств.
- Провести практическую работу по данной теме и подвести её итоги.
Я думаю полученные мною, знания и навыки помогут мне решить вопрос: искать ОДЗ или не надо? Я перестану делать ошибки, научившись правильно делать ОДЗ. Получится ли у меня это, покажет время, точнее ЕГЭ[4].
Глава 1
Что такое ОДЗ?
ОДЗ - это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.
Важно. Для нахождения ОДЗ мы не решаем пример! Мы решаем кусочки примера для нахождения запретных мест.
Некоторые запреты в математике. Таких запретных действий в математике очень мало. Но их не все помнят…
- Выражения, состоящие под знаком чётной кратности или должно быть>0 или равно нулю , ОДЗ:f(x)
- Выражение, стоящее в знаменателе дроби не может быть равно нулю , ОДЗ:f(x)
- |f(x)|=g(x), ОДЗ: g(x) 0
Как записать ОДЗ? Очень просто. Всегда рядом с примером пишите ОДЗ. Под этими известными буквами, глядя на исходное уравнение, записываем значения х, которые разрешены для исходного примера. Преобразование примера может изменить ОДЗ и, соответственно ответ.
Алгоритм нахождения ОДЗ:
- Определите вид запрета.
- Найти значения, при которых выражение не имеет смысла.
- Исключить эти значения из множества действительных чисел R[6].
Решить уравнение: =
|
Без ОДЗ |
С ОДЗ |
|
= = х-9=1-х х+х=9+1 2х=10 х=5 Ответ: х=5 Оценка 2 |
= ОДЗ: => =>
Ответ: корней нет Оценка 5 |
Область допустимых значений оберегает нас от таких серьёзных ошибок. Честно говоря, именно из-за ОДЗ многие «ударники» превращаются в «троечников». Считая, что поиск и учёт ОДЗ малозначимым шагом в решении, они пропускают его, а потом удивляются: «почему учитель поставил 2?». Да потому и поставил, что ответ неверен! Это не «придирки» учителя, а вполне конкретная ошибка, такая же как неверное вычисление или потерянный знак[7].
Дополнительные уравнения:
а) = ; б) -42=14х+ ; в) =0; г) |x-5|=2x-2 [5]
Глава 2
ОДЗ. Зачем? Когда? Как?
Область допустимых значений – есть решение
- ОДЗ представляет собой пустое множество, а значит, исходный пример не имеет решений
Ответ: корней нет.
Ответ: корней нет.
ОДЗ: х 0
0, уравнение не имеет корней
Ответ: корней нет.
Дополнительные примеры:
а) + =5; б) + =23х-18; в) =0[6].
- В ОДЗ находится одно или несколько чисел, и несложная подстановка быстро определяет корни.
ОДЗ: х=2, х=3
Проверка: х=2, + , 0<1, верно
Проверка: х=3, + , 0<1, верно.
Ответ: х=2, х=3[8].
Проверка: х=0, > , 0>0, неверно
Проверка: х=1, > , 1>0, верно
Ответ: х=1.
Проверка: + =3, 0=3, неверно.
Ответ: корней нет.
Дополнительные примеры:
а) = ; б) + =0; в) + =х -1[5]
Опасность ОДЗ
Заметим, тождественные преобразования могут:
- не влиять на ОДЗ;
- приводить к расширенному ОДЗ;
- приводить к сужению ОДЗ.
Известно также, что в результате некоторых преобразований, изменяющих исходное ОДЗ, может привести к неверным решениям.
Давайте поясним каждый случай примером.
1) Рассмотрим выражение х +4х+7х, ОДЗ переменной х для этого есть множество R. Приведём подобные слагаемые. В результате оно примет вид x2+11x. Очевидно, ОДЗ переменной x этого выражения тоже является множество R. Таким образом, проведенное преобразование не изменило ОДЗ.
2) Возьмем уравнение x+ - =0. В этом случае ОДЗ: x≠0. Это выражение тоже содержит подобные слагаемые, после приведения которых, приходим к выражению x, для которого ОДЗ есть R. Что мы видим: в результате проведенного преобразования произошло расширение ОДЗ (к ОДЗ переменной x для исходного выражения добавилось число нуль).
3) Возьмем выражение . ОДЗ переменной x определяется неравенством (x−5)·(x−2)≥0, ОДЗ: (−∞, 2]∪[5, +∞). А теперь преобразуем исходное выражение к виду . ОДЗ переменной x для этого выражения определяет система линейных неравенств , решение которой дает множество [5, +∞). Таким образом, в результате проведенного преобразования произошло сужение ОДЗ с множества (−∞, 2]∪[5, +∞) до множества [5, +∞)[9].
Решим уравнение:
а) 3х+ = +15. Перенесём дробь
ОДЗ: х-5 0, х 5
3х+ - =15
х=5, 5 ОДЗ. Ответ: корней нет.
б) =0 х-х=0 =0. Снова ловушка!
ОДЗ: х-3 0, х 3. Ответ: х-любое число, кроме х=3.
в) , ОДЗ: х .
Сокращение дробей даёт =0, х=0. Ловушка! Ответ: корней нет[6].
Дополнительные примеры: а) =0, б) =0;
в) 214х+ = +642, г) + =92[5].
Вывод. Итак, на каждом шаге преобразования выражения постоянно спрашивайте себя: «Не изменяет ли это преобразование ОДЗ»? Если не изменяет, то выполняйте его. Если сужает, то откажитесь от него. А если расширяет, то выполняйте его, но оставайтесь в рамках ОДЗ переменных для исходного выражения. Самый верный шаг – найдите сразу ОДЗ[2].
Необязательность ОДЗ
Решим уравнение:
а) - =2
=2+ , f(x)= - убывает, g(x)=2+ - возрастает
Значит, уравнение имеет не более одного корня. Решаем методом подбора: х=-1. Ответ: х=-1.
б) =13-х, f(x)= - возрастает, g(x)= 13-х – убывает, значит, уравнение имеет не более одного корня. Решаем методом подбора: х=11.
ОДЗ: х-7≥0 х≥7
Квадратный корень всегда неотрицателен, значит 13-х>0.
Ответ: х=11.
в) + =0
Так как система, достаточно решить одно из уравнений и проверить, подставив во второе.
х +3х-4=0 а+в+с=0 х =1, х = , значит х =-4
х=1: 1 +12 1 -11 1-2=0
х=-4: (-4) +12 (-4) -11 (-4)-2 0. Ответ: х=1.
Вывод: нахождение ОДЗ не всегда является обязательным, часто не нужно, а иногда и невозможно - и всё это без какого бы то ни было ущерба для решения примера. Но я согласен с тем, что на уроках математики от нас требуют нахождения ОДЗ в каждом примере[3].
Нестандартные уравнения
1)|х+4|=2х-10 ОДЗ: 2х-10 0, х 5
|
х+4=2х-10 |
-х-4=2х-10 |
|
х-2х=-10-4 -х=-14 х=14 |
-х-2х=4-10 -3х=-6 х=2, 2 ОДЗ |
Ответ: х=14.
2) - =23х-18 ОДЗ:
Так как полученная система решений не имеет, то область решений не имеет, таким образом, область определения уравнения не содержит ни одного корня, значит, данное уравнение не имеет корней[8].
3) + = - ОДЗ: х
- = =
+ =
f(x)= + - возрастает , g(x)= - убывает
(так как если h(x) возрастает, то - убывает).
Уравнение имеет не более одного корня. Метод подбора. Ответ: х=2[4].
4) + + + =2
ОДЗ: х=2,х=0. Подставляем числа 2 и 0 в уравнение.
+ + + =2, 2=2
+ + + .
Ответ: х=2[4].
Глава 3
Практическая работа «ОДЗ: когда, зачем и как?»
Было дано 10 уравнений, 2 неравенства. Количество учащихся – 28. Справились - 14 %, опасность ОДЗ(учли) – 68 %, необязательность (учли)-36%.
|
|
ОДЗ -решение |
Опасность ОДЗ |
Необязательность ОДЗ |
Нестандартные уравнения и неравенства |
|
Иррациональные уравнения |
61% |
68% |
82% |
43% |
|
Дробные уравнения |
69% |
89% |
86% |
50% |
|
Неравенства |
50% |
89% |
82% |
64% |
|
Уравнения, содержащие модуль |
86% |
96% |
43% |
61% |
Заключение
Тема работы раскрыта. Цель: выявление: когда, зачем и как находить ОДЗ – раскрыта. В исследовательской работе рассмотрены уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для выпускников хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ.
Задачи, поставленные в работе, решены. Разобраны стандартные и нестандартные уравнения и неравенства. Проведена практическая работа по теме «ОДЗ. Когда? Зачем и как?» И подведены итоги. Полученные читателями, знания и навыки помогут им решить вопрос- искать ОДЗ или не надо?[10]
Каждому выражению с переменными соответствует область допустимых значений (ОДЗ) переменных, которую ОБЯЗАТЕЛЬНО нужно учитывать при работе с этим выражением. Акцент на слове «обязательно» сделан не случайно: при решении примеров и задач халатное отношение к ОДЗ может привести к получению неверных результатов.
Овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ[4].
Литература
М.Я. Выгодский «Справочник по элементарной математике». М.: «Наука», 1966.
- Газета «Математика» №17. 2002.
- Г.И. Глейзер «История математики в школе VII-VIII классы». М.: «Просвещение», 1982.
- Л.О. Денищева и др. «ЕГЭ. Математика. Универсальные материалы для подготовки учащихся/ФИПИ» - М.: «Интеллект-центр», 2009.
- [Электронный ресурс]/Режим доступа: Материалы сайтов www.fipi.ru, www.eg
- Область допустимых значений – есть решение [Электронный ресурс]/Режим доступа: rudocs.exdat.com›docs/index-16853.html
- ОДЗ – область допустимых значений, как найти ОДЗ [Электронный ресурс]/Режим доступа: cleverstudents.ru›expressions/odz.html
- Область допустимых значений: теория и практика [Электронный ресурс]/Режим доступа: pandia.ru›text/78/083/13650.php
- Что такое ОДЗ [Электронный ресурс]/ Режим доступа: www.cleverstudents.ru›odz.html
- Что такое ОДЗ и как его искать - объяснение и пример. Электронный ресурс]/ Режим доступа: cos-cos.ru›math/82/
Приложение 1
Практическая работа «ОДЗ: когда, зачем и как?»
|
Вариант 1 |
Вариант 2 |
|
|
= 0 |
|
9х+ = + 27
|
≤ + |
|
+ = –1
|
|
|
│х+14│= 2 – 2х
|
= |
|
|
8х + = – 32 |
|
≥ +
|
+ = 1 |
|
= 0
|
│3-х│=1 – 3х |
Приложение 2
Ответы к заданиям практической работы «ОДЗ: когда, зачем и как?»
|
Вариант 1 |
Вариант 2 |
|
Ответ: корней нет |
ОДЗ: х 5 Ответ: х-любое число, кроме х=5 |
|
9х+ = +27 ОДЗ: х≠3 Ответ: корней нет |
≤+ ОДЗ:→ ОДЗ: х=-3, х=5. Ответ:-3;5. |
|
+=-1 у= –убывает, у= –возрастает Значит, уравнение имеет не более одного корня. Ответ: х=6. |
ОДЗ: → →х≥5 → Ответ:х≥5, х≤-6. |
|
│х+14│=2-2х ОДЗ:2-2х≥0, х≤1 х=-4, х=16, 16 не принадлежит ОДЗ Ответ:-4 |
= – убывает, –возрастает Уравнение имеет не более одного корня. Ответ: корней нет. |
|
0, ОДЗ: х≥3,х≤2 Ответ: х≥3,х≤2 |
8х+ = -32, ОДЗ: х≠-4. Ответ: корней нет. |
|
≥+ ОДЗ:→ х=7, х=1. Ответ: решений нет |
+=1 - возрастает, - убывает Ответ: х=2. |
|
=0 ОДЗ: х≠15 Ответ: х- любое число, кроме х=15. |
│3-х│=1-3х, ОДЗ: 1-3х≥0, х≤ х=-1, х=1 не принадлежит ОДЗ. Ответ: х=-1. |
Просмотров работы: 148
school-science.ru
Как решать дробные уравнения? | Александр Будников
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё один основной тип уравнений – дробные уравнения.
Иногда их называют более научно и солидно - дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Итак, начнём наше знакомство!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, - это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то эти уравнения к дробным не относятся! Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что в знаменателях дробей – только числа! Четвёрка и пятёрка. И ни один из знаменателей не содержит икса.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на наличие дроби 1/5. Опять же, по причине того, что деления на неизвестное нигде нету.
В общем, вы поняли.
Как решать дробные уравнения?
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. Каким же именно образом? Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В нашем случае это – умножение всего уравнения на одно и то же выражение. В чём суть?
Нам надо помножить обе части уравнения на одно и то же выражение. Но не просто выражение, а такое, чтобы все знаменатели посокращались! Одним махом.) И дальше, без знаменателей, жизнь станет гораздо проще и веселее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум – перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как страшный сон! Так делают только в одном случае – при решении дробно-рациональных неравенств методом интервалов. А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) В левой части для ликвидации знаменателя нам необходимо умножение на х+3, а в правой – на 3. Но умножать обе части уравнения математика позволяет только на одно и то же выражение! Поэтому нам надо скомбинировать такое выражение, которое одновременно делится как на х+3, так и на 3. Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на 3(х+3).
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, распишу детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача – от дробей избавиться, а не париться с раскрытием скобок!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь, с чувством глубокого удовлетворения, производим сокращение:
Вот и отлично. Дробей больше нет. После сокращения получилось безобидное линейное уравнение:
6 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решим теперь следующий примерчик, чуть посложнее:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации надо левую часть домножить на знаменатель. То есть, просто на х. Но тогда и правую часть тоже надо домножить на х: так уж второе тождественное преобразование требует. Вот и домножаем! Всю левую часть и всю правую часть:
С чистой совестью сокращаем икс слева и получаем уравнение уже безо всяких дробей, в линеечку.
20 = х(9-х)
А вот теперь, когда все дроби исчезли напрочь, раскрываем скобки:
20 = 9х – х2
Следующим шагом переносим всё влево:
х2 – 9х + 20 = 0
Получили классическое квадратное уравнение. Решаем через дискриминант (или по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь – квадратным. А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся что-нибудь типа 3=3 или 1=4. Надеюсь, такой сюрприз вас уже нисколько не удивит.) Если всё же удивит, то прогуляйтесь по ссылочке:
Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее – особые случаи при решении линейных уравнений.
Разумеется, иногда встречаются и неожиданности. И одну из них мы как раз рассмотрим прямо сейчас.
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить наше уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, тупо взять и перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на это длинное выражение. Но… Может быть, есть выражение попроще?)
Вынужден открыть тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители.)
А попробуем-ка разложить каждый из знаменателей на множители! Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим икс за скобку и получаем:
х2+2х = х(х+2)
Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножить обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и на х(х+2). Вот и умножаем.
Напоминаю, что эта вертикальная палочка с умножением означает, что обе части нашего уравнения мы умножаем на х(х+2).
Расписываю подробно. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем – вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Малые скобки в числителях не раскрываем! Они нам сейчас для сокращения понадобятся! Кстати, прошу обратить внимание на один важный момент: в числителе первой дроби выражение (х-3) при умножении я взял в скобки! Почему? Потому, что мы умножаем весь числитель целиком! Дело всё в том, что частенько народ числитель записывает вот так:
х – 3∙х(х+2)
Это категорически неверно. Дальше можно не решать…
Но у нас всё верно, надо дорешивать. С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x – 3x – 6 + 3 – х = 0
x2 – 2x – 3 = 0
И снова получили квадратное уравнение.) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители – обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора!
Кстати сказать, если бы мы домножили всё уравнение на произведение знаменателей
x(x2+2x)(x+2),
то, в конце концов, тоже всё получилось бы. Всё лишнее посокращалось. Если ошибок по дороге не наляпать.) Но зачем же упускать шанс облегчить себе жизнь, правда?
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение этих трёх дробных уравнений вовсе не гарантирует успех в решении всех остальных уравнений. Даже очень простых, подобных этим. К сожалению…
ОДЗ в дробных уравнениях.
А сейчас мы с вами научимся обходить одну из главных ловушек на ЕГЭ! Попадаются в неё все – и троечники, и отличники. Но для начала посмотрим, попадёте вы в неё или нет.)
Допустим, надо решить вот такое простое уравнение:
Дело уже привычное и знакомое. Умножаем всё уравнение на знаменатель (х+1) и получаем:
Напоминаю, что со скобками (х+1) работаем целиком, как с одной буквой! Производим умножение:
Сокращаем знаменатель:
3x2 + 2x – 1 = 5(x+1)
Раскрываем оставшиеся скобки, переносим всё влево, приводим подобные:
3x2 + 2x – 1 = 5x + 5
3x2 - 3x – 6 = 0
Делим всё уравнение на 3 и получаем:
х2 – х – 2 = 0
Самое обычное квадратное уравнение. Решаем и получаем два корня:
х1 = -1
х2 = 2
Предположим, в задании на ЕГЭ сказано записать в ответе меньший из корней, если корней более одного. Что писать будем? Если вы решили, что ответ -1, то вы попали в ловушку. И задание вам не засчитают, да. Зря старались… Правильный ответ был 2. Два, а не минус один…
Так в чём же дело? А вы попробуйте проверку сделать. Подставьте каждый из найденных корней в исходное уравнение. И, если при х=2 у вас всё славненько срастётся, получится тождество 5=5, то при х=-1 получится деление на ноль! Чего делать нельзя категорически. Нет такой операции ни в природе, ни в математике… Что это значит? Это значит, что х=-1 – так называемый посторонний корень. Или лишний корень. Он не является корнем нашего исходного уравнения и в ответе никак не учитывается. Его мы просто отбрасываем. Окончательный корень один. А именно: х=2.
Так, стоп! Нам же говорили, что всё уравнение можно умножать на одно и то же выражение! Это же тождественное преобразование!
Да, тождественное. Я не спорю. Но при одном маленьком ограничении, которое многие поначалу просто игнорируют. А именно – выражение, на которое умножаем (делим), отлично от нуля! А скобочка (х+1) при х=-1 обращается в ноль! Так что всё честно.
И что нам теперь делать? Совсем не умножать? Тогда мы вообще ничего не решим! Каждый раз проверку делать? Это с ума сойдёшь. Особенно, если уравнение навороченное или корни некрасивые (иррациональные, к примеру).
Нет, мы с вами пойдём красивым и элегантным путём. Обратимся за помощью к трём волшебным буквам! Догадались? Да! Это ОДЗ! Область Допустимых Значений.
Что такое ОДЗ? Это такие значения икса, которые могут быть в принципе. Или которые разрешены для данного примера.
Например, в уравнении
мы ещё пока не знаем, чему равен икс, верно? Мы уравнение пока не решили. Но зато мы железно знаем, что икс не может равняться нулю ни в коем случае! На ноль делить нельзя. На любое другое число – целое, дробное, отрицательное, иррациональное – ради бога. А вот на ноль – никак. Стало быть, в этом примере ОДЗ: х – любое число, кроме нуля. Идея ясна?
Как записывать ОДЗ? Как искать ОДЗ? Тоже легко. На первом этапе всегда внимательно осматриваем исходный пример и ищем опасные места. Что значит опасные места? Это места, где возможны запретные действия. Действия, которые при каких-то значениях икса могут оказаться недопустимыми с точки зрения математики. В нашей теме такое действие всего одно – деление. Нельзя делить на ноль. Есть ещё ограничения в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках.
Как только опасные места найдены, рядышком с примером выписываем условия, которые не приводят к бессмыслице. После этого мы, глядя на эти условия, наоборот, вычисляем запретные иксы. И исключаем их из ОДЗ. Вот и всё.
Я специально акцентирую внимание на словах «исходный пример». Любое преобразование может изменить ОДЗ, и мы можем получить неверный ответ.
Важно! Для поиска ОДЗ мы не решаем пример! Мы решаем всего лишь маленькие кусочки примера для нахождения запретных иксов. "Многа букаффф", да. Но на практике вся процедура выглядит до ужаса элементарно.
Итак, берём наше уравнение:
Ничего пока что не решаем, а именно внимательно осматриваем исходное уравнение. Осмотрев, мы сразу замечаем операцию деления на х+1. Это потенциально опасная операция: при каких-то значениях икса выражение х+1 может оказаться равным нулю. На который делить нельзя. Поэтому обезопасим себя вот такой записью:
х+1 ≠ 0
х ≠ -1
Вот и всё. Это и будет ОДЗ для нашего уравнения. Вот и вся процедура нахождения ОДЗ. На практике запись и нахождение ОДЗ обычно оформляют так:
Вот так. Как только мы себя обезопасили такой записью, дальше мы уже можем делать с уравнением всё что хотим – переносить члены, домножать, делить... Вот и домножаем всё уравнение на (х+1), чтобы ликвидировать дробь. Это по-прежнему будет не совсем тождественным преобразованием, но все вредные последствия от нарушения тождественности мы исключим по ОДЗ.
Умножаем:
3x2 + 2x – 1 = 5(x+1)
А теперь разберёмся, в какой же момент мы с вами попали в засаду с появлением постороннего корня х=-1. Как раз в момент домножения всего уравнения на (х+1) и ликвидации знаменателя. Знаменатель исчез, и вместе с ним исчезли и соответствующие ограничения на иксы. Бесследно. И для нового уравнения, уже без дробей, на икс уже не накладывается никаких запретов! Любым теперь может быть икс…
В математике это явление называется расширение ОДЗ.
Но теперь мы уже с вами народ бдительный. Исходные ограничения (х≠-1) мы записали и сохранили.
И дальше спокойно решаем уравнение безо всяких дробей и получаем два корня:
х1 = -1
х2 = 2
А вот теперь сопоставляем наши результаты и условия ОДЗ и видим в наших кандидатах на ответ один из иксов в качестве запретного! Минус один. Это означает, что в окончательный ответ его включать нельзя. Это посторонний корень, появившийся в процессе решения без нашего желания. Стало быть, минус единицу мы безжалостно вычёркиваем и в ответ не включаем. Вот и всё.)
А в трёх других уравнениях? Там что, нет ОДЗ? Есть, конечно. Есть деление на икс – есть и ОДЗ.
В первом уравнении:
Во втором уравнении:
В третьем уравнении:
Я специально в этих примерах ничего не сказал про ОДЗ. Чтобы вас не испугать раньше времени.) В этих трёх уравнениях ОДЗ никак не сказалась на ответе. Повезло. Так бывает.) Но в заданиях ОГЭ и ЕГЭ ОДЗ, как правило, влияет на ответ! Так что мы с ОДЗ дружить будем! И во всех темах, где необходимо, мы будем про ОДЗ вспоминать. Чтобы не упасть лицом в грязь.)
Итак, подведём итог нашим умозаключениям практическими советами.
Для успешного решения любого дробного уравнения необходимо выполнить (правильно) пять пунктов:
1) Разложить все знаменатели на множители (если требуется). До упора. Переписать пример с учётом этого факта.
2) Внимательно исследовать пример на наличие опасных операций. Найти ОДЗ, записать рядышком с примером и временно (до конца решения) забыть про неё.
3) Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли напрочь.
4) Выполнить это самое умножение и решить пример уже безо всяких дробей. Получить решения (кандидаты в ответ).
5) Вспомнить про ОДЗ и сопоставить найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
Всё понятно или что-то не очень? Отдельно ещё раз заострю своё (и ваше) внимание на предварительном разложении знаменателей дробей на множители.
Во-первых, если знаменатель дроби УЖЕ разложен на множители, то искать ОДЗ для неё становится несравненно проще. Почему проще – поясняю на примере. Допустим, дана нам вот такая дробь:
Как нам найти ОДЗ для этой дроби? Очень просто. Знаменатель не должен равняться нулю. Так и записываем:
x2 – 3x ≠ 0
Как теперь найти запретные иксы? Очевидно, надо решить неполное квадратное уравнение:
x2 – 3x = 0
Напоминаю, для его успешного решения достаточно вынести икс за скобки:
х(х-3) = 0
Приравняв в уме каждый множитель к нулю, получим наши иксы:
х1 = 0
х2 = 3
Вспоминаем, что найденные иксы – это запретные значения! И исключаем их из ОДЗ:
х ≠ 0; х ≠ 3
Ну как? Много возни? Согласен, много. А теперь смотрите, насколько всё проще и быстрее, когда знаменатель предварительно разложен на множители:
Это была первая причина. А вот вторая. Когда знаменатели всех дробей предварительно разложены на множители, гораздо проще и быстрее становится искать то самое выражение, на которое надо умножать всё уравнение, чтобы ликвидировать все дроби! Этот момент вы уже прочувствовали на третьем примере.
Замечу, что разложение на множители – единственное безопасное действие, никак не сказывающееся на ОДЗ исходного примера. В отличие от сокращения и приведения подобных, к примеру. Посему – раскладываем, не стесняемся.)
А теперь, вооружившись таким мощным супероружием, как ОДЗ, и практическими советами, разберём очередной пример. Супердетально разберём!
Решить уравнение:
Решаем строго по пунктам. Выполняем пункт первый:
1) Разложить все знаменатели на множители (если требуется). До упора. Переписать пример с учётом этого факта.
Знаменатели наших дробей НЕ разложены на множители. Приступаем сначала к разложению. Вынесение общего множителя за скобки и формула разности квадратов – мощные штуки!)
2x – x2 = x(2-x)
2x + x2 = x(2+x)
4 – x2 = 22 – x2 = (2-x)(2+x)
Вот так. А теперь переписываем уравнение с учётом наших разложений:
2) Внимательно исследовать исходный пример на наличие опасных операций. Найти ОДЗ, записать рядышком с примером и временно (до конца решения) забыть про неё.
Итак, начинаем осматривать исходный пример на наличие опасных операций.
Внимание! Не складываем дроби, не приводим подобные, не сокращаем!!!
Подобные преобразования запросто могут изменить ОДЗ, и мы запросто можем получить неверный ответ! Оно нам надо?! Ещё раз напоминаю: до поиска ОДЗ с исходным примером мы не делаем НИЧЕГО! Кроме разложения на множители. Оно – безопасно и даже полезно.)
Берём и именно осматриваем наш исходный пример. И замечаем три опасных места: каждая из дробей таит в себе возможное деление на ноль.
Вот и пишем:
Знак системы (фигурная скобка) здесь не зря поставлен. Она означает, что все три неравенства должны выполняться одновременно! Мы ведь ОДЗ записываем не для каждой дроби по отдельности, а для всего примера целиком.)
Решаем теперь эти неравенства методом "от противного". То есть, делаем из неравенств уравнения:
x(2-x) = 0
x(2+x) = 0
(2-x)(2+x) = 0
Из этих трёх уравнений мы и будем искать запретные иксы. Уравнения очень простые: произведение равно нулю, когда хотя бы один из множителей равен нулю. Вот и приравниваем в уме или на черновике каждый множитель к нулю.
Для первого уравнения получаем: x1 = 0; x2 = 2.
Вспомнив, что это запретные иксы, получим: х ≠ 0; x ≠ 2.
Точно так же решаются и два оставшихся уравнения.
Для второго уравнения получаем: x ≠ 0; x ≠ -2.
И, наконец, для третьего уравнения получаем: x ≠ 2; x ≠ -2.
Видно, что некоторые запретные значения иксов повторяются. Разумеется, для записи ОДЗ мы их не будем дублировать. В результате запись ОДЗ для нашего уравнения будет выглядеть вот так:
ОДЗ:
Видите, насколько полезно предварительно раскладывать знаменатели на множители! В уме ОДЗ записывается!
Можно приступать к третьему пункту.
3) Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли напрочь.
На что такое надо умножить всё уравнение, чтобы все дроби пропали напрочь? И вот тут разложение на множители тоже здорово играет на руку!
Понятно, что для ликвидации первой дроби, надо её домножать на x(2-x), вторую – на x(2+x) и третью - на (2-x)(2+x). А для того, чтобы сразу сократились бы все дроби, надо скомбинировать выражение, которое одинаково хорошо делится и на х(2-х), и на х(2+х), и на (2-х)(2+х).
Вот оно, это выражение:
х(2-x)(2+x)
Как же я до него додумался? Очень просто: составил произведение всех неповторяющихся множителей всех знаменателей. Чтобы ничего не забыть и лишнего не взять.) Приступаем к четвёртому пункту:
4) Выполнить это самое умножение и решить пример уже безо всяких дробей. Получить решения (кандидаты в ответ).
Итак, умножаем:
И снова, чтобы не запутаться и не ошибиться, используем скобки:
Производим умножение. Раскрываем большие скобки, малые – не трогаем!
Сокращаем все дроби:
2 + x + (x-4)(2-x) = 2x
Как обычно, раскрываем скобки, приводим подобные и собираем все члены слева:
2 + x + 2x – x2 – 8 + 4x – 2x = 0
-x2 + 5x – 6 = 0
Помним, что минус перед квадратом икса крайне неудобен для дальнейшей работы, посему умножаем всё на (-1):
x2 – 5x + 6 = 0
Решаем простенькое квадратное уравнение и получаем корни:
x1 = 2
x2 = 3
Нашли кандидатов в ответ. Самое время вспомнить про ОДЗ. Про самый последний пункт:
5) Вспомнить про ОДЗ и сопоставить найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
Итак, наши решения:
x1 = 2
x2 = 3
Условия ОДЗ:
Сопоставляем и… Опаньки! А ведь двойка – запретное значение! Нас не проведёшь! ОДЗ – штука жёсткая. В отвал двойку!
Окончательный ответ: х = 3.
Вот, собственно, и всё, что я хотел сказать. Как вы видите, всё достаточно просто. Если не просто механически зазубрить алгоритм, а понимать смысл каждого его пункта. А теперь решаем самостоятельно:
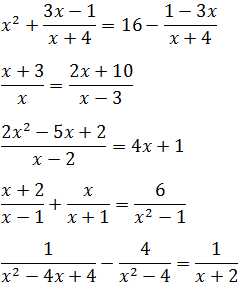
Ответы (по традиции, в беспорядке):
x = 3
x = -1
x = 4
x1 = -1; x2 = -9
x = -2
Всё совпало! Поздравляю! У вас иксов поболее будет? Хм… Про ОДЗ не забыли, случаем? Кое-какие корни выбрасывать надо! ОДЗ учли, а всё равно не выходит? Да-а-а... Проблемка. Такие уравнения надо уметь решать: слишком уж они популярны во многих темах математики. Особенно – в текстовых задачках! Но не отчаивайтесь! Перечитайте урок ещё раз и прогуляйтесь по смежным темам: разложение на множители, квадратные уравнения, линейные уравнения и (особенно!) тождественные преобразования уравнений. И всё получится.)
abudnikov.ru
Как найти область допустимых значений
Область возможных значений функции невозможно путать с областью значений функции. Если первое – это все х, при которых уравнение либо неравенство может быть решено, то второе – все значения функции, то есть у. Об области возможных значений надобно помнить неизменно, от того что частенько обнаруженные значения х лукаво оказываются вне этой общности и следственно не могут быть решением уравнения.

Вам понадобится
- — уравнение либо неравенство с переменной.
Инструкция
1. Первоначально в качестве области возможных значений возьмите бесконечность. То есть представьте, что уравнение дозволено решить при всех х. Позже этого, применяя несколько несложных запретов математики (невозможно разделять на нуль, выражения под корнем четной степени и логарифма должно быть огромнее нуля), исключайте из ОДЗ недопустимые значения переменной.
2. Если переменная х заключена в выражении под корень четной степени, поставьте условие: выражение под корнем обязаны быть поменьше нуля. После этого решите это неравенство, обнаруженный промежуток исключите из области возможных значений . Обратите внимание, не нужно решать все уравнение – при поиске ОДЗ вы решаете лишь его маленький ломтик.
3. Обратите внимание на знак деления. Если в выражении есть знаменатель, содержащий переменную, приравняйте его к нулю и решите полученное уравнение. Исключите полученные значения переменной из области возможных значений .
4. Если в выражении есть знак логарифма с переменной в основании, непременно поставьте следующее лимитация: основание неизменно должно быть огромнее нуля и не равно единице. Если же переменная стоит под знаком логарифма, укажите, что все выражение в скобках должно быть огромнее единицы. Решите полученные небольшие уравнения и исключите недопустимые значения из ОДЗ.
5. Если в уравнении либо неравенстве несколько корней четной степени, операций деления либо логарифмов, обнаружьте недопустимые значений отдельно для всего выражения. После этого объедините решение, вычитая все полученные итоги из области возможных значений .
6. Даже если вы обнаружили ОДЗ и полученные при решении уравнения корни удовлетворяют ему, это не неизменно значит, что эти значения х являются решением, следственно неизменно проверяйте правильность решения подстановкой. Скажем, испробуйте решить следующее уравнение: ? (2х-1)=-х. В область возможных значений тут войдут все числа, удовлетворяющие 2х-1?0, то есть х?1/2. Для решения уравнения возведите обе части в квадрат, позже облегчений у вас получится один корень х=1. Обратите внимание, данный корень входит в ОДЗ, но при подстановке вы удостоверитесь, что он не является решением уравнения. Окончательный результат – корней нет.
jprosto.ru