Перевод десятичной дроби в обыкновенную. Перевод дроби в
Перевести обыкновенную дробь в десятичную дробь
Перевод обыкновенной дроби в десятичную дробь
Несократимую дробь можно преобразовать в десятичную только тогда, когда разложение знаменателя b на простые множители не содержит чисел, отличных от 2 и 5.
В результате преобразования получается бесконечная периодическая десятичная дробь .
Простой способ преобразования
Воспользуйтесь калькулятором, разделите числитель дроби на знаменатель в результате получите десятичную дробь.
Пример Преобразовать дробь в десятичную дробь
Разделим с помощью калькулятора числить на знаменатель, получим .
Альтернативный метод преобразования
Привести знаменатель дроби к 10, 100, 1000, 10000 и т.д. Найдите число которое преобразует знаменатель к числу из списка (10, 100, 1000, и т.д.). Умножьте числитель и знаменатель на данное число, затем запишите числитель в виде десятичной дроби, расположив запятую(точку) в зависимости от количества нулей в знаменателе.
В примере показано как переводить дробь в десятичную дробь ручным способом.
Пример Преобразовать дробь в десятичную.
.
.
calcs.su
Перевод дроби в десятичную дробь
При переводе обыкновенной дроби в десятичную удобнее всего работать с сокращенными дробями, у которых уже выделена целая часть, тогда не приходится ее высчитывать отдельно, и числитель и знаменатель максимально просты. Как это сделать, можно посмотреть в разделах «Перевод неправильной дроби в смешанную дробь» и «Сокращение дробей», или воспользоваться он-лайн калькулятором для дроби в том виде, в котором она есть.
Дроби делятся на два вида – те, которые можно перевести в десятичную дробь без потери данных, и те, которые при обычном раскладе не считаются переводимыми, но их также можно представить в десятичном виде с округлением до определенного количества знаков после запятой. Первый вид дробей имеет следующую отличительную особенность – их знаменатель состоит только из простых множителей 2 и 5. Определить это можно, полностью разделив его на простые множители в калькуляторе «Разложение на множители». Для перевода таких дробей в десятичный вид необходимо привести их к минимальному десятичному знаменателю 10, 100, 1000 и т.д. Для этого количество простых множителей 2 и 5 должно быть одинаковым, например, для дроби дополнительным множителем до 100 будет 5, так как 20 раскладывается на множители 20=22×5, и для одинакового количества множителей необходим еще один – 5. После того как дробь приведена к необходимому знаменателю, ее можно записывать в десятичный вид – целая часть остается неизменной, а числитель записывается после запятой в таком порядке, чтобы количество знаков после запятой соответствовало количеству нулей в знаменателе.
Второй вид дробей содержит в знаменателе хотя бы один сторонний множитель и не подлежит подобным превращениям. Для того чтобы привести его в десятичный вид, необходимо просто разделить числитель на знаменатель до следующей цифры после необходимого количества знаков после запятой, например делением в столбик. Эта дополнительная цифра служит индикатором того, в какую сторону округлять полученную десятичную дробь.
geleot.ru
Перевод дробей из одного вида в другой
Перевод дробей из одного вида в другой. Рекомендую посмотреть весь список материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.
1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:
Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:
Примеры:
2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).
При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:
*Подробнее:
15:13 = 1 остаток 2
4:3 = 1 остаток 1
9:5 = 1 остаток 4
А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:
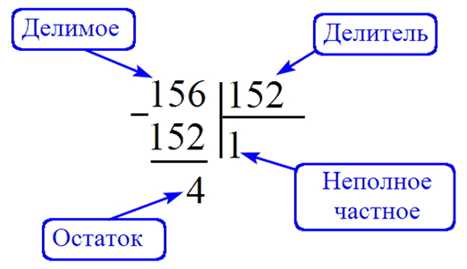
Например:
*Числитель у нас – это делимое, знаменатель – это делитель.
Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):
3. Десятичную переводим в обыкновенную.
Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015
Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:
*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.
4. Обыкновенную переводим в десятичную.
Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:
Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:
Если имеется целая часть, то тоже ничего сложного:
Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:
А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:
На какие числа умножать числитель и знаменатель?
Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:

Так вы сможете всегда определить переводится ли дробь в десятичную. Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:
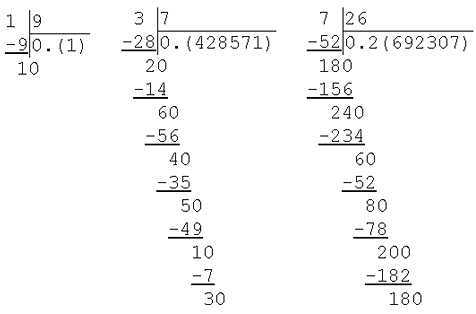
На этом всё! Успеха вам!
Делитесь информацией в социальных сетях!
matematikalegko.ru
Перевод десятичной дроби в обыкновенную
Любую десятичную дробь можно представить в виде обыкновенной дроби. Для этого надо просто записать её со знаменателем.
Главное правило в переводе десятичной дроби в обыкновенную – как читается десятичная дробь, так и пишется обыкновенная. Например:
2,3 – две целых три десятых
Так как дробь имеет целую часть, то перевести её мы можем или в смешанное число или в неправильную дробь:
Если у десятичной дроби нет целой части, например:
0,75 – ноль целых семьдесят пять сотых,
то её можно сразу перевести в правильную обыкновенную дробь и, если нужно (по необходимости), сократить:
Перевод обыкновенной дроби в десятичную
Не любую обыкновенную дробь можно перевести в десятичную, так как чтобы записать обыкновенную дробь в виде десятичной, надо привести её к знаменателю, представляющему собой единицу с одним или несколькими нулями, например: 10, 100, 1000 и т. д. Если разложить такой знаменатель на простые множители, то получится одинаковое количество двоек и пятёрок:
10 = 2 · 5
100 = 10 · 10 = 2 · 5 · 2 · 5
1000 = 10 · 10 · 10 = 2 · 5 · 2 · 5 · 2 · 5
Никаких других простых множителей эти разложения не содержат, следовательно:
Обыкновенную дробь можно представить в виде десятичной только в том случае, если её знаменатель не содержит никаких других множителей, кроме 2 и 5.
Возьмём дробь:
При разложении её знаменателя на простые множители получается произведение 2 · 2:
Если домножить его на две пятёрки, чтобы уравнять количество пятёрок с двойками, то получится один из нужных знаменателей – 100. Чтобы получить дробь равную данной, то числитель тоже надо будет умножить на произведение двух пятёрок:
| 3 | = | 3 · 5 · 5 | = | 75 | = | 0,75 |
| 4 | 2 · 2 · 5 · 5 | 100 |
Рассмотрим ещё одну дробь:
При разложении её знаменателя на простые множители получается произведение 2 · 7, содержащее число 7:
Множитель 7 будет присутствовать в знаменателе, на какие бы целые числа его ни умножали, поэтому произведение, содержащее только двойки и пятёрки никогда не получится. Значит данную дробь нельзя привести ни к одному из нужных знаменателей: 10, 100, 1000 и так далее. То есть её нельзя представить в виде десятичной.
Обыкновенную несократимую дробь нельзя представить в виде десятичной, если её знаменатель содержит хотя бы один простой множитель, отличный от 2 и 5.
Обратите внимание, что в правиле написано только о несократимых дробях, потому что некоторые дроби после сокращения, можно представить в виде десятичных. Рассмотрим две дроби:
Первая дробь является несократимой и, как мы уже выяснили, её нельзя представить в виде десятичной. Во второй дроби числитель и знаменатель можно сократить на 7, то есть на тот простой множитель, который мешает в первой дроби:
| 7 | = | 7 : 7 | = | 1 |
| 14 | 14 : 7 | 2 |
Теперь осталось только умножить оба члена дроби на 5, чтобы получить 10 в знаменателе, и можно будет переводить дробь в десятичную:
| 1 | = | 1 · 5 | 5 | = | 0,5 | |
| 2 | 2 · 5 | 10 |
naobumium.info
Перевод обыкновенной дроби в десятичную - Арифметика
Обыкновенную дробь можно перевести в конечнуюдесятичную дробь, если её знаменатель раскладывается только на множители 2 и 5, которые могут повторятся.
Примеры:
Дробь 11/40 можно преобразовать в конечную десятичную. Её знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
Хотим напомнить, что множители 2 и 5 называются простыми, то есть они делятся только на самих себя и на 1.
Перевести обыкновенную дробь в десятичную можно несколькими способами.
Первый способ перевода
Чтобы превратить дробь в десятичную, нужно и числитель и знаменатель умножить на одно и то же число, так чтобы в знаменателе получилось 10, 100, 1000 и т.д.
Прежде чем приниматься за работу, не забудьте проверить, можно ли вообще превратить данную дробь в десятичную (см. предыдущую страницу).
Примеры:
Убеждаемся, что дробь можно привести в конечную десятичную.
Умножаем числитель и знаменатель на 5. В знаменателе получим 100.
Еще пример:
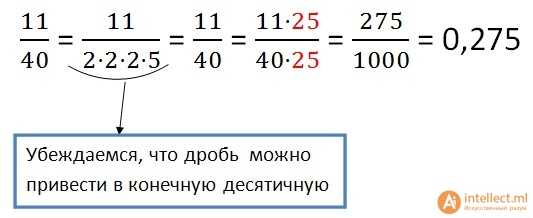
Второй способ перевода
Второй способ более сложный, но применяется чаще первого. Для того, чтобы его использовать нужно вспомнить деление уголком.
Чтобы перевести обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
Пример:
Убеждаемся, что дробь можно перевести в конечную десятичную.
Делим уголком числитель на знаменатель.
Ниже приведен список дробей со знаменателями, которые чаще других встречаются в заданиях. Вы облегчите себе работу, если их просто выучите.
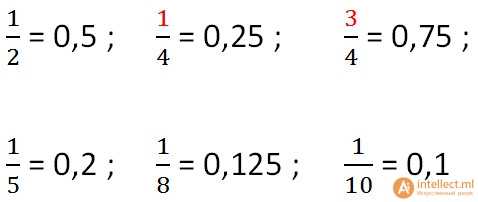
intellect.ml
не так уж и сложно — журнал "Рутвет"
Оглавление:
- Как возникли дроби
- Появление простых дробей
- Индийские цифры
- Позиционная система и десятичные дроби
- Двоичная система: математика опять без дробей
- Алгоритм перевода обыкновенных дробей в десятичные
- Примеры перевода
Но если все знают, что 3/4 = 0,75, то запись 1/3 = 0,3333… или 1/3 = 0,(3) может вызвать недоумение у человека, отвыкшего считать без калькулятора, даже если он в свое время успешно прошел школьный курс арифметики. Так нужно ли уметь переводить дроби друг в друга? Что-то там помнится из пятого класса, это такая скука… Не такая уж и скука, между прочим, и может пригодиться. Для начала обратимся к истории.
Как возникли дроби
Впервые дроби появились в Древнем Вавилоне где-то за 2000 лет до новой эры и были шестидесятиричными: их знаменатель равнялся 60. Математикой в Вавилоне занимались жрецы, они же в своих занятиях столкнулись со случаями, когда нужно было знать соотношение чисел, друг на друга не делящихся.
Жрецы просто подобрали число, которое достаточно развитый человек еще может удержать в уме, имеющее максимальное количество простых делителей. В самом деле, 60 делится и на 2, и на 3, и на 5, и соответственно, на все кратные им числа без остатка. Знаменатель 60 вавилонских дробей был своего рода эталоном для сравнения чисел.
Но для средних умов – купцов, ремесленников, строителей – основание 60 было все же слишком большим. И плохо согласовывалось с удобным для практики счетом на пальцах рук, которых 10. Да и особых значков для цифр тогда еще не было; все действия записывались словами. Представляете? Лучше не надо.
Появление простых дробей
Следующий шаг сделали древние греки, которые свели математику к геометрическим построениям. Это было, по тем временам, очень наглядно. Развел ножки циркуля, отложил отрезок пять раз. Затем его же – семь раз. И сразу видно, какой насколько больше. Расположил отрезки параллельно на определенном расстоянии, провел прямые через их концы – видно, какой угол получился.
Современному человеку, даже специалисту, трудно представить себе такую математику, поэтому многие грандиозные сооружения и замечательные машины древности приписываются сегодня то ли инопланетянам, то ли атлантам, то ли еще кому-то, кроме тех людей, которые их на самом деле сделали.
Геометризация математики позволяла сравнивать без какого-либо выделенного эталона любые числа, делятся они друг на друга или нет. Поэтому дроби стали простыми: 3/11; 123/768 и т.п.
До поры, до времени, пока для практики не требовались очень большие и очень малые числа, простые дроби были вне конкуренции.
Индийские цифры
Революцию в математике произвели не позднее V в. н. э. индийцы, придумав отдельные значки для цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Они шли от того же счета на пальцах, поэтому и значков придумали 10, а не 12 или 60. Достаточно удобно – два простых делителя, 2 и 5 – и без труда может запомнить любой. 12 (дюжина) перед 10 не имеет преимущества, т.к. у него тоже два простых делителя: 2 и 3, а значков для записи требуется на два больше.
Не позднее VII в. индийские цифры пришли в Китай и к арабам, а от тех, в Х в. – в Европу. Поэтому у нас индийские цифры называются арабскими.
Позиционная система и десятичные дроби
Индийские цифры позволяли записывать любое, сколь угодно большое число в т. наз. позиционной системе. Каждая цифра слева от предыдущей считалась умноженной на 10. 458 = 4х10х10 + 5х10 + 8. 10 в таком случае – основание системы счисления. И оно же самым естественным образом становилось универсальным знаменателем дробей, вроде вавилонского 60, но доступным обычному уму.
Появление позиционной системы во многом способствовало прогрессу науки и техники. Геометрия циркуля и линейки тут выдохлась – ее точность была ограниченной. А математика становилась все более изощренной и оперировала все более абстрактными понятиями.
В 1617 г. английский математик Непер предложил целую (основание) и дробную (мантиссу) часть десятичной дроби разделять запятой, а знаменатель 10 не писать вовсе, раз он везде один и тот же. Теперь десятичной дробью можно было записывать и сколь угодно малые числа. А для невообразимо малых позже придумали экспоненциальную форму записи. Скажем, 7,37Е-7 будет 0,000000737. Она же оказалась удобной для отображения на дисплеях электронных устройств.
Есть ли у простых дробей будущее? Казалось бы, нет. Куда там, если даже десятичные отступают под натиском процентов. Но не так-то все просто.
Двоичная система: математика опять без дробей
Цифровые компьютеры работают в системе счисления с основанием 2 (двоичной). В ней всего две цифры – 0 и 1; включено/выключено; верно/неверно, а каждая «левая» цифра считается умноженной на 2 относительно «правой». Перевод двоичного кода в обычные десятичные числа делают специальные программы.
Кстати, в двоичной системе дробей вовсе нет, т.к. 1 на себя всегда делится с результатом тоже 1.
Развитие компьютерной техники идет по пути все большей наглядности результатов. Если в 50-х годах специалист по ЭВМ обязан был уметь читать двоичный код на перфоленте так же, как обычные цифры на бумаге, то теперь он же на цифровую распечатку может и не взглянуть – на дисплее ясно видно, в геометрических образах, как идет процесс.
Остается только удивляться гению древних греков, сразу поставивших наглядность во главу угла. Что бы они натворили, будь у них компьютеры?
Алгоритм перевода обыкновенных дробей в десятичные
Перевод обыкновенных дробей в десятичные делается последовательным делением числителя на знаменатель, затем остатка, умноженного на 10, опять на знаменатель, следующего остатка, опять умноженного на 10, снова на знаменатель, и так до тех пор, пока остатка не останется, либо не выявится период десятичной дроби, либо не будет достигнута заданная точность.
Числа, получившиеся до первого остатка, пишем до запятой; они дадут основание десятичной дроби.
Числа, получившиеся от деления остатков, умноженных на 10, пишем после запятой. Они дадут мантиссу.
Скажем сразу: не всякую простую дробь можно перевести в десятичную точно. Если знаменатель делится на 3, 7 или другое, не кратное 2 или 5, число, то получится бесконечная периодическая десятичная дробь. Период такой дроби принято брать в круглые скобки. Скажем, 2/3 = 0,(6). Либо округлять с заданной точностью, наподобие 0,6667. Период может оказаться очень длинным, тогда останавливаются на следующем, после достижения заданной точности, знаке. 2/3 с точностью в 1% будет 0,667.
Есть числа, которые невозможно выразить отношением любых целых чисел. Математики называют их иррациональными. Это всем известное ПИ – отношение длины окружности к ее диаметру, основание натурального логарифма е и другие. Такие числа записываются бесконечной непериодической десятичной дробью. Останавливаются по достижении нужной точности + один следующий знак.
Примеры перевода
Числитель больше знаменателя
Допустим, есть дробь 362/128.
- 362:128 = 2 + 106 в остатке (362 = 128х2 + 106 = 256 +106). Мантисса десятичной дроби будет равна 2, т.к. сразу же получился остаток.
- 106х10 = 1060:128 = 1060 – (128х8 = 1024) = 8 + 36 в остатке. 8 – первая цифра после запятой.
- 36х10 = 360:128 = 2 + 104 в остатке. 2 – вторая цифра после запятой.
- 1040:128 = 8 + 16 в остатке. 8 – третья цифра после запятой.
- 160:128 = 1 + 32 в остатке. 1 – четвертая цифра после запятой.
- 320:128 = 2 + 64 в остатке. 2 – пятая цифра после запятой.
- 640:128 = 5 – шестая цифра после запятой, остатка не осталось, и мы имеем 362/128 = 2,828125.
Числитель меньше знаменателя
Считаем числитель первым остатком. Сразу умножаем его на 10, и пишем ноль с запятой (0, ). Если числитель опять меньше знаменателя, считаем его вторым остатком, умножаем опять на 10 (всего 100), а после запятой дописываем еще ноль, и так далее, пока не получим числитель больше знаменателя. Тогда делим, как в примере первом.
3/8 = ?. 3х10 = 30; 30:8 = 3 + 6 в остатке; 6х10 = 60; 60:8 = 7 + 4 в остатке; 4х10 = 40; 40:8 = 5.
3/8 = 0,375.
Тогда 3/80 будет 0,0375; 3/800 = 0,00375 и т.д.
Нули после запятой до первой отличной от нуля цифры – незначащие, а первая отличная от нуля цифра после запятой и следующие за ней называются значащими. Если дописывать после последней значащей цифры нули, они значащими не будут.
Если проделать описанную процедуру для дроби, допустим, 9/14 (вспомним, 14 делится на 7), то получим 0,64285714285714285714… Числа в мантиссе …285714… будут повторяться до бесконечности; у нас получилась бесконечная периодическая десятичная дробь. Такую дробь для полной точности записывают так: 0,64(285714).
Иррациональное число при переводе обычных дробей в десятичные получиться не может, т.к. иррациональные числа отношением целых чисел не выражаются. Если мы считаем и считаем, а периода все не видно, значит, он слишком длинный и нужно остановиться на заданной точности.
Есть правило: чем больше у знаменателя простых делителей, тем длиннее окажется период. А простые делители – это делители из простых чисел, которые делятся только на самих себя и на 1. 1, 2, 3, 5, 7, 9, 11, 13, 17, 23, 29 – это все простые числа. Математики до сих пор не знают, конечно ли количество простых чисел и по каким законам они распределяются в числовом ряду.
Не правда ли, хоть и сложновато, но вовсе не так уж и скучно?
www.rutvet.ru
Как перевести обыкновенную дробь в десятичную
Рассмотрим, как перевести обыкновенную дробь в десятичную. Не всегда можно записать обыкновенную дробь в виде конечной десятичной. Таким образом, перевод обыкновенной дроби в десятичную в процессе вычислений может привести к неточному результату.
Правило:
Чтобы обыкновенную дробь перевести в десятичную, нужно ее числитель разделить на знаменатель.
Примеры:

Однако, при делении, например, 2 на 7, мы получим бесконечную дробь:
Результат можно округлить с той или иной точностью:
Но в математике, как правило, требуются не приближенные, а точные значения. Поэтому полезно помнить, когда перевод обыкновенной дроби в десятичную приводит к получению точного ответа.
Любое число можно разделить на 2, 5 и числа, которые можно разложить на множители только из двоек и пятерок.
Например, 4=2∙2, 8=2∙2∙2, 10=2∙5, 16=2∙2∙2∙2, 20=2∙2∙5, 25=5∙5, 32=2∙2∙2∙2∙2∙2, 40=2∙2∙2∙5, 50= 2∙5∙5, 64==2∙2∙2∙2∙2∙2, 80=2∙2∙2∙2∙5, 100=2∙5∙2∙5 и т.д.
Таким образом, при выполнении действий, содержащих и десятичные, и обыкновенные дроби, перевести обыкновенную дробь в десятичную удобно только в том случае, когда знаменатель обыкновенной дроби представляет собой произведение только двоек и пятерок. В остальных случаях следует от десятичной дроби перейти к обыкновенной.
www.uznateshe.ru