Как найти площадь поверхности куба? Площадь грани формула куба
периметр, площадь, содержание, объем куба (формула и онлайн-расчет)
Расчет
Введите данные в какое-либо поле, остальные параметры будут расчитаны автоматически.Если в какой-либо области изменения данных, другие автоматически пересчитываются. В качестве десятичной запятой можно использовать как запятую, так и точку.
Результат выводится в тех-же единицах, что и вводите данные. Например если ввели в сантиметрах, то и результат будет в них-же.
Обнаруженны NaN, проверьте, что вы ввели в поле корректные данные, то есть без букв и других символов.
Формулы
| Периметр куба(общая длина ребра) | O = | 12 × a | [m] |
| Площадь одной стороны | P = | a × a = a² | [m²] |
| Площадь куба(поверхность) | Q = | 6 × P1 = 6 × a² | |
| Объем куба | V = | a × a × a = a³ | [m³] |
| Диагоналная(стороны/стены) | u2 = | a √2 ≈ a × 1,41 | [m] |
| Диагональ куба(пространственная/тело) | u3 = | a √3 ≈ a × 1,73 | [m] |
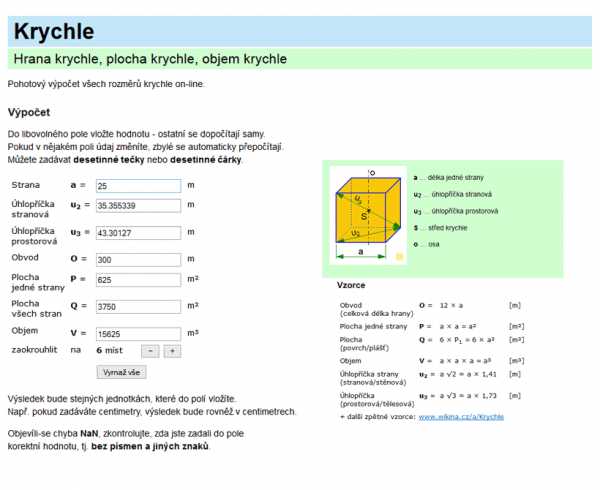
a … длина одной стороны
u2 … диагоналная стороны
u3 … пространство по диагонали
S … центр куба
o … ось
Куб и шар
Диагональный пространственное (u3) = диаметр сферы на кубе ограниченный Сторона куба (a) = диаметр шара вписанного в куб
Другие формулы для вычисления сферы, вписанной или очерченной смотрите страницу, посвященную онлайн расчет шара.Расчет куба онлайн
Расчет периферии всех ребер куба. Калькулятор для расчета общей площади или поверхности куба и передачи к содержанию или объему куба, шаблон куба. площадь или длина окружности оболочки или содержимого. Расчет объема куба онлайн. Формула для вычисления куба.
Ссылки
Как рассчитать ...
Выделенные жирным шрифтом ссылки уже работают. Другие пока содержат только лишь формулу.Могло бы вас заинтересовать
kub.wikina.ru
Немного информации о кубе и о способах того, как вычислить площадь поверхности куба :: SYL.ru
Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от этого ничего не изменится. А формулы для него всегда легко запоминаются. И неважно, что нужно найти - объем или площадь поверхности куба. В последнем случае даже не нужно учить что-то новое. Достаточно помнить только формулу площади квадрата.
Что такое площадь?
Эту величину принято обозначать латинской буквой S. Причем это справедливо для школьных предметов, таких как физика и математика. Измеряется она в квадратных единицах длины. Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.
Так что же такое площадь? Это величина, которая является числовой характеристикой рассматриваемой фигуры или объемного тела. Она показывает размер ее поверхности, которая ограничена сторонами фигуры.
Какая фигура называется кубом?
Эта фигура является многогранником. Причем непростым. Он правильный, то есть у него все элементы равны друг другу. Будь то стороны или грани. Каждая поверхность куба представляет собой квадрат.
Другое название куба — правильный гексаэдр, если по-русски, то шестигранник. Он может быть образован из четырехугольной призмы или параллелепипеда. При соблюдении условия, когда все ребра равны и углы образуют 90 градусов.
Эта фигура настолько гармонична, что часто используется в быту. Например, первые игрушки малыша — кубики. А забава для тех, кто постарше, — кубик Рубика.

Как связан куб с другими фигурами и телами?
Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.
В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.
Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.
Метод 1: вычисление площади куба по его ребру
Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».
Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S1.
Для удобства лучше задать номера всем формулам. Эта будет первой.
Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a2. Ее номер 2.

Метод 2: как вычислить площадь, если известен объем тела
Этот способ сводится к тому, чтобы сосчитать длину ребра по известному объему. И потом уже воспользоваться известной формулой, которая здесь обозначена цифрой 2.
Из математического выражения для объема гексаэдра выводится то, по которому можно сосчитать длину ребра. Вот она:
Нумерация продолжается, и здесь уже цифра 3.
Теперь его можно вычислить и подставить во вторую формулу. Если действовать по нормам математики, то нужно вывести такое выражение:
Это формула площади всей поверхности куба, которой можно воспользоваться, если известен объем. Номер этой записи 4.
Метод 3: расчет площади по диагонали куба
Для того чтобы рассчитать площадь полной поверхности куба, также потребуется вывести ребро через известную диагональ. Здесь используется формула для главной диагонали гексаэдра:
Это формула №5.
Из нее легко вывести выражение для ребра куба:
Это шестая формула. После его вычисления можно снова воспользоваться формулой под вторым номером. Но лучше записать такую:
Она оказывается пронумерованной цифрой 7. Если внимательно посмотреть, то можно заметить, что последняя формула удобнее, чем поэтапный расчет.
Метод 4: как воспользоваться радиусом вписанной или описанной окружности для вычисления площади куба
Если обозначить радиус описанной около гексаэдра окружности буквой R, то площадь поверхности куба будет легко вычислить по такой формуле:
Ее порядковый номер 8. Она легко получается благодаря тому, что диаметр окружности полностью совпадает с главной диагональю.
Обозначив радиус вписанной окружности латинской буквой r, можно получить такую формулу для площади всей поверхности гексаэдра:
Это формула №9.
Несколько слов о боковой поверхности гексаэдра
Если в задаче требуется найти площадь боковой поверхности куба, то нужно воспользоваться уже описанным выше приемом. Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:
Ее номер 10. Если даны какие-то другие величины, то поступают аналогично описанным выше методам.
Примеры задач
Условие первой. Известна площадь поверхности куба. Она равна 200 см². Необходимо вычислить главную диагональ куба.
Решение.
1 способ. Нужно воспользоваться формулой, которая обозначена цифрой 2. Из нее будет несложно вывести «а». Эта математическая запись будет выглядеть как квадратный корень из частного, равного S на 6. После подстановки чисел получается:
а = √ (200/6) = √ (100/3) = 10 √3 (см).
Пятая формула позволяет сразу вычислить главную диагональ куба. Для этого нужно значение ребра умножить на √3. Это просто. В ответе получается, что диагональ равна 10 см.
2 способ. На случай если забылась формула для диагонали, но помнится теорема Пифагора.
Аналогично тому, как было в первом способе, найти ребро. Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.
х² = а² + а², где х — диагональ квадрата.
d² = х² + а² = а² + а² + а² = 3 а². Из этой записи легко видно, как получается формула для диагонали. А дальше все расчеты будут, как в первом способе. Он немножко длиннее, но позволяет не запоминать формулу, а получить ее самостоятельно.
Ответ: диагональ куба равна 10 см.
Условие второй. По известной площади поверхности, которая равна 54 см2, вычислить объем куба.
Решение.
Пользуясь формулой под вторым номером, нужно узнать значение ребра куба. То, как это делается, подробно описано в первом способе решения предыдущей задачи. Проведя все вычисления, получим, что а = 3 см.
Теперь нужно воспользоваться формулой для объема куба, в которой длина ребра возводится в третью степень. Значит, объем будет считаться так: V = 33 = 27 см3.
Ответ: объем куба равен 27 см3.

Условие третьей. Требуется найти ребро куба, для которого выполняется следующее условие. При увеличении ребра на 9 единиц площадь всей поверхности увеличивается на 594.
Решение.
Поскольку явных чисел в задаче не дано, только разности между тем, что было, и тем, что стало, то нужно ввести дополнительные обозначения. Это несложно. Пусть искомая величина будет равна «а». Тогда увеличенное ребро куба будет равно (а + 9).
Зная это, нужно записать формулу для площади поверхности куба два раза. Первая - для начального значения ребра - совпадет с той, которая пронумерована цифрой 2. Вторая будет немного отличаться. В ней вместо «а» нужно записать сумму (а + 9). Так как в задаче идет речь о разности площадей, то нужно вычесть из большей площади меньшую:
6 * (а + 9)2 - 6 * а2 = 594.
Нужно провести преобразования. Сначала вынести за скобку 6 в левой части равенства, а потом упростить то, что останется в скобках. А именно (а + 9)2 - а2. Здесь записана разность квадратов, которую можно преобразовать так: (а + 9 - а)(а + 9 + а). После упрощения выражения получается 9(2а + 9).
Теперь его нужно умножить на 6, то есть то число, что было перед скобкой, и приравнять к 594: 54(2а + 9) = 594. Это линейное уравнение с одной неизвестной. Его легко решить. Сначала нужно раскрыть скобки, а потом перенести в левую часть равенства слагаемое с неизвестной величиной, а числа — в правую. Получится уравнение: 2а = 2. Из него видно, что искомая величина равна 1.
Ответ: а = 1.
www.syl.ru
Формулы площади поверхности тел
Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Содержание статьи:
Формула площади поверхности призмы
Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).
Sбок = ph=pl
р — периметр основания;
h — высота;
l — боковое ребро.
Формула площади поверхности куба
Площадь боковой поверхности куба равна числу боковых граней умноженному на квадрат ребра.
Sбок = 4a2
Площадь полной поверхности куба равна числу всех граней куба умноженному на квадрат ребра.
P = 6a2
а — ребро куба.
Формула площади поверхности пирамиды
1) Правильная пирамида:
Sбок = 1/2pA
p — периметр основания;
A — апофема.
Sбок = S/cos φ
S — площадь основания;
φ — угол между боковой гранью и основанием пирамиды.
Sбок = Sгр n
Sгр — площадь одной боковой грани;n — количество боковых граней пирамиды.
2) Правильная усеченная пирамида:
Sбок = 1/2(p1 + p2)A
p1 ,p2— периметры оснований;
A — апофема.
Р = Sбок + S1 + S2
Р — площадь полной поверхности правильной усеченной пирамиды;
Sбок— площадь боковой поверхности правильной усеченной пирамиды;
S1 + S2 — площади оснований.
Формула площади поверхности цилиндра
Sбок = 2πrh = πdh
P = 2πr2+2πrh = 2π(r+h)
P — площадь полной поверхности цилиндра;
r — радиус цилиндра;
d — диаметр цилиндра;
h — высота цилиндра.
Формула площади поверхности конуса
1) Прямой круговой конус:
Sбок = πrl = 1/2 πdl
P = πr2 + πrl= πr(r+l)
P — площадь полной поверхности конуса;
r -радиус конуса;
d -диаметр конуса;
l — образующая конуса.
2) Усеченный прямой круговой конус:
Sбок = πl(r1 + r2) = 1/2πl(d1 + d2)
P = πl(r1 + r2) + π(r1 + r2)
P — площадь полной поверхности усеченного конуса;
r1, r2— радиусы оснований усеченного конуса;
d1, d2— диаметры оснований усеченного конуса;
l — образующая усеченного конуса.
Формула площади поверхности шара (сферы)
Шар — тело, созданное вращением полукруга вокруг диаметра.
Сфера — поверхность шара.
P = 4πR2 = πD2
Формула площади поверхности сферического сегмента
Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.
Sсф. сегм. = 2πRh = π(a2 + h3)
Формула площади поверхности шарового сегмента
Шаровой сегмент — часть шара, что отсекается от шара плоскостью, и ограничивается кругом (основание шарового сегмента) и сферическим сегментом.
Sшар. сегм. = π(2Rh+a2)=π(h3+2a2)
R — радиус шара;
D — диаметр шара;
h — высота сегмента;
a — радиус основания сегмента.
Материалы по теме:
Поделиться с друзьями:
Загрузка...matemonline.com
Ответы@Mail.Ru: Как найти площадь куба?
Объём на высоту и ширину
Площадь куба - это сумма площади всех шести его сторон. Вот формула: 6 x s2, где "s" это сторона куба <img data-big="1" data-lsrc="//otvet.imgsmail.ru/download/194147873_73de0f2c33c8c660e3c75aca1de9b587_120x120.jpg" src="//otvet.imgsmail.ru/download/194147873_73de0f2c33c8c660e3c75aca1de9b587_800.jpg">
У куба 8 граней. В основе каждой грани квадрат с одинаковыми сторонами. Пусть длина сторон равна а. Тогда площадь поверхности куба будет равна сумме всех площадей поверхностей. Те 8*а*а.
Куб - правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра и грани куба равны. Площадь поверхности куба равна квадрату длины его грани умноженному на шесть. Формула для вычисления площади куба S = 6 a2 где S - площадь куба, a - длина грани куба.
S = 6 граней * S (одной грани) = 6 * а * а
Площадь куба - это сумма площадей его граней. Формула S = 6 * a * a Быстро вычислить можно тут - <a rel="nofollow" href="http://www.center-pss.ru/math/plkuba.htm" target="_blank">http://www.center-pss.ru/math/plkuba.htm</a>
touch.otvet.mail.ru
Площадь стороны куба | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Площадь стороны куба является площадью квадрата и представляет собой сторону квадрата, возведенную во вторую степень. Так как сторона любого квадрата-грани в кубе – это ребро куба, следовательно, ребро куба, выраженное через площадь стороны, приобретает вид квадратного корня из площади. a=√S
Если необходимо рассчитать площадь боковой или полной поверхности куба, то это можно сделать, не проводя расчетов по вычислению ребра. Площадь боковой поверхности куба представлена четырьмя боковыми гранями, площадь которых уже известна, а площадь полной поверхности – всеми шестью гранями куба. S_(б.п.)=4S S_(п.п.)=6S
Для расчета всех последующих параметров понадобится полученная формула для ребра куба через площадь грани. Объем куба вычисляется как возведение ребра в третью степень, следовательно, объем куба через площадь грани равен квадратному корню из площади в третьей степени. V=a^3=√(S^3 )
Чтобы вычислить периметр куба, нужно умножить его ребро на двенадцать, то есть умножить на двенадцать квадратный корень площади стороны куба.. P=12a=12√S
Диагональ стороны куба через теорему Пифагора выражается, как сторона квадрата или ребро куба, умноженное на корень из двух. Таким образом, диагональ стороны куба через площадь имеет вид квадратного корня из удвоенной площади. d=a√2=√2S
Чтобы вычислить диагональ куба, нужно провести диагональ в его основании, тогда они в совокупности с боковым ребром образуют прямоугольный треугольник, в котором диагональ куба будет равна ребру, умноженному на корень из тех. Так как ребро должно быть выражено через площадь грани, диагональ куба равна квадратному корню из утроенной площади. (рис.2.1) a^2+d^2=D^2 D^2=a^2+2a^2 D^2=3a^2 D=a√3=√3S
Сфера, вписанная в куб, обладает диаметром, равном по значению ребру куба, значит радиус такой сферы будет равен половине ребра или половине квадратного корня из площади стороны куба. (рис. 2.2) r=a/2=√S/2
Чтобы вычислить радиус сферы, описанной вокруг куба, необходимо разделить пополам его диагональ. Так как диагональ куба равна квадратному корню из утроенной площади стороны куба, то радиус описанной сферы будет его половиной. (рис.2.3) R=D/2=√3S/2
geleot.ru
Как найти площадь поверхности куба?
Куб представляет собой объемный вариант квадрата. Зная длину ребра куба (а), можно воспользоваться наиболее распространенной формулой по определению площади поверхности (S). Исходя из того, что площадь квадрата соответствует длине возведенной в квадрат грани, и у куба их шесть, получается: S = 6∙a². Эта формула определяет площадь полной поверхности куба.
Способы определения площади куба
- Если задан объем (V) пространства, что ограничен сторонами куба, а длина ребра неизвестна, то площадь (S) определяется таким образом.
Когда единственно известная величина фигуры, представляет собой возведенную в третью степень длину ребра, тогда размер длины стороны каждой грани куба определяют посредством извлечения кубического корня из имеющегося параметра. Формула площади поверхности куба имеет вид: S = 6∙(³√V)².
- Когда задана длина диагонали гексаэдра (L), тогда длину одной грани можно легко вычислить, а вместе с ней и площадь фигуры. Диагональ определяют так: L/v3. А площадь куба поэтому вычисляется так: S = 6∙(L/√3)² = 2∙L², что очень удобно при расчетах.
- Как найти площадь поверхности куба, когда указан радиус описанной около гексаэдра сферы (R)? Просто! Необходимо только применить формулу такую: S = 8∙R²= 2∙(2∙R)². Такое возможно благодаря тому, что диагональ куба соответствует параметру диаметра сферы.
- Зная радиус вписанной в гексаэдр окружности, формулу площади поверхности куба записывают так: S = 24∙r².
Площадь боковой поверхности куба
S = s1+s2+s3+s4, в которой слагаемые представляют собой площади четырех параллелограммов соответственно, которые образуют боковую поверхность параллелепипеда.
Формула площади боковой поверхности куба может быть представлена как S = P•h при условии, что задан прямой параллелепипед, с известным периметром основания P и высотой h.
Когда расчеты нужно провести по прямоугольному п
elhow.ru
Как найти объём куба если нам известна только площадь верхней грани?
S^(3/2) то есть (корень из S) в третьей степени
Обём куба вычисляется по формуле V=а3, где V — объём куба, а — длина его ребра. Нам необходимо знать длину ребра куба, чтобы высчитать его объём. Площадь куба вычисляется: S=6a2, следовательно мы можем узнать длину его ребра немного переобразовав формулу площади куба: . Если известна площадь грани куба — она равна площади квадрата, тогда используем формулу S=a2. Узнаем длину ребра по формуле: . Получившееся значение а подставляете в первую формулу и получаете значение объёма куба.
ну так сразу надо писать что куб)
допустим площадь 36 см значит ребро куба 6 см так как 6 умножить на 6 равно 36 см то есть объём куба равен 6 см в третий степени
touch.otvet.mail.ru











