Матричные уравнения и их решение. Решить матричные уравнения
Решение матричных уравнений: теория и примеры
Матричным уравнением называется уравнение вида
A ⋅ X = B
или
X ⋅ A = B,
где A и B - известные матрицы, X - неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E - единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:
.
Как решить матричное уравнение во втором случае? Если дано уравнение
X ⋅ A = B,
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X. То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A.
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
A ⋅ X ⋅ B = C,
является
.
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:
.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Найдём матрицу, обратную матрице B.
Сначала найдём определитель матрицы B:
.
Найдём алгебраические дополнения матрицы B:
Составим матрицу алгебраических дополнений матрицы B:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:
.
Находим матрицу, обратную матрице B:
Находим неизвестную матрицу:
Поделиться с друзьями
Начало темы "Матрицы"
Продолжение темы "Матрицы"
Другие темы линейной алгебры
function-x.ru
Матричные уравнения и их решение
Определение и формулы матричных уравнений
ОПРЕДЕЛЕНИЕ Матричным уравнением называется уравнение, состоящее из нескольких матриц-коэффициентов и неизвестной матрицы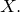
Простейшим матричным уравнением есть уравнение вида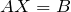 
или 
,
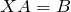где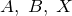 
Алгоритм решения матричных уравнений
1. Матричное уравнение приводится к одному из простейших уравнений:
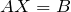или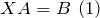 
где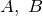 
— известные матрицы, 
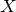— искомая (неизвестная) матрица.
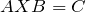
Чтобы привести произвольное матричное уравнение к одному из видов (1), надо все известные матрицы по свойствам уравнений перенести вправо, а неизвестную матрицу в левой части и свести подобные.
2. Разрешаем полученное простейшее уравнение относительно неизвестной матрицы .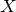
2.1 Если в результате преобразований получили простейшее уравнение 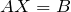, то необходимо левую и правую часть этого равенства слева умножить на обратную матрицу 
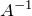к матрице 
:
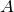![\[AX=B\Rightarrow A^{-1} AX=A^{-1} B\Rightarrow EX=A^{-1} B\Rightarrow X=A^{-1} B\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-cb2ade56b2ec2a919fd73beb0077ada3_l3.png "Rendered by QuickLaTeX.com")
Поскольку умножение матриц некоммутативно, то нужно строго соблюдать умножение слева или справа, иначе это влияет на результат.
2.2 Для простейшего уравнения 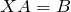после умножения справа на обратную матрицу 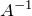получаем:
![\[XA=B\Rightarrow XAA^{-1} =BA^{-1} \Rightarrow XE=BA^{-1} \Rightarrow X=BA^{-1} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-05ad7a50849415650e2b4ee2b20d55af_l3.png "Rendered by QuickLaTeX.com")
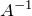находится либо методом союзной матрицы, либо методом присоединенной матрицы. 3. Далее вычисляется одно из произведени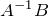й 
или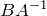 
, что и определяет искомую матрицу.
4. Делаем проверку, для этого подставляем найденную матрицу 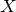в исходное уравнение.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Решение матричных уравнений
Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана»
(КФ МГТУ им. Н.Э. Баумана)
Влайков Н.Д.
Решение матричных уравнений
Методические указания для проведения упражнений
по курсу аналитической геометрии
Калуга 2011г.
Содержание.
Цели занятия стр.4
План занятия стр.4
Необходимые теоретические сведения стр.5
Практическая часть стр.6
Контроль освоения пройденного материала стр.10
Домашнее задание стр.11
Количество часов: 2
Цели занятия:
Систематизировать полученные теоретические знания о видах матричных уравнений и способах их решения.
Применить на практике методы решения матричных уравнений.
План занятия:
Кратко изложить теоретический материал.
Решить матричное уравнение видаметодом с использованием обратной матрицы.
Решить матричное уравнение видаметодом, основанным на элементарных преобразованиях строк матрицы.
Сравнить использованные методы.
Решить матричное уравнение видаметодом с использованием обратной матрицы.
Решить матричное уравнение вида методом с использованием обратной матрицы.
Проверить выполнение текущего домашнего задания.
Провести проверочную работу.
Представить тему следующего семинарского занятия.
Выдать текущее домашнее задание.
Необходимые теоретические сведения.
Рассмотрим два вида матричных уравнений относительно неизвестной матрицы :и, где матрицыи- известны, причем- квадратная и невырожденная.
Опр. Некоторую матрицу называют решением матричного уравнения относительно неизвестной матрицы , если при ее подстановке вместоматричное уравнение превращается в тождество.
Рассмотрим уравнение .
Первый метод предполагает вычисление обратной матрицы и дает запись решения матричного уравнения в виде. Причем данное решение единственно.
Второй метод основан на элементарных преобразованиях строк блочной матрицы и имеет своей целью преобразование ее к виду, в котором вместо матрицыстоит единичная матрица. Тогда матрицаи будет решением уравнения.
Проверка ответа выполняется подстановкой найденного решения в исходное уравнение.
Матричное уравнение так же можно решить двумя способами. Если известна матрица, то умножаем справа наматричное уравнениеи после очевидных преобразований получаем ответ в виде произведения двух матриц. Другой метод решения матричного уравнениясостоит в транспонировании его левой и правой частей,. После введения новой неизвестной матрицыполучаем уравнение вида, которое решается методом элементарных преобразований.
Практическая часть.
Пример 1. Решить матричное уравнение: ,
где
; .
Решение.
1-ый способ. Найдем решение, используя обратную матрицу:
Решение ищем в виде ;
Найдем матрицу (например, при помощи присоединенной матрицы)
.
Таким образом, получим:
.
2-ой способ. Найдем решение методом элементарных преобразований:
Запишем матрицу и выполним элементарные преобразования ее строк с целью привести ее к виду .
.
Следовательно, .
Проверка осуществляется подстановкой в исходное уравнение:
- Верно.
Пример 2. Решить матричное уравнение: ,
где
; ;.
Решение.
Если для матриц исуществуют обратные матрицыисоответственно, умножим обе части уравнения слева на, справа на. В результате получим:
. Учитывая, что ,
(- единичная матрица) можно записать:. Так как
- единичная матрица, окончательно имеем уравнение:
где матрица - решение уравнения.
Если же хотя бы одна из матриц илине имеет обратную, уравнение не имеет решения.
Для матрицы найдем или докажем, что она не существует.
а) обратная матрица существует.
б) .
в) Найдем алгебраические дополнения для матрицы и составим из них присоединенную матрицу:
.
г) Известно, что ; тогда
.
Для матрицы найдем или докажем, что она не существует.
а) обратная матрица существует.
б) .
в) Найдем алгебраические дополнения для матрицы и составим из них присоединенную матрицу:
.
г) По формуле ;
.
Найдем неизвестную матрицу .
.
Ответ:.
Решить матричные уравнения:
№2.121(2.39)
. Отв.:
№2.122(2.40)
. Отв.:
№2.123(2.41)
. Отв.:
№2.124(2.42)
. Отв.:
№2.125(2.43)
. Отв.:
Представление темы следующего семинара.
Решение систем линейных однородных уравнений.
Контроль освоения пройденного материала.
Проверочная работа 5 минут. Участвует 4 студента с четными номерами по журналу, начиная с №10
Задание:
| Вар№1 Выполнить действия: | Вар№2 Выполнить действия: |
| Вар№3 Найти матрицу обратную данной:
| Вар№4 Найти матрицу обратную данной: |
Ответы:
| Вар№1 Выполнить действия:
| Вар№2 Выполнить действия: |
| Вар№3 Найти матрицу обратную данной:
| Вар№4 Найти матрицу обратную данной: |
Домашнее задание.
1.Решить матричное уравнение :
1) ; .
2) ; .
2.Решить матричное уравнение :
1) ;;.
2) ;;.
3.Проработка лекций на темы:
Системы линейных алгебраических уравнений (СЛАУ). Координатная, матричная и векторная формы записи. Критерий Кронекера — Капелли совместности СЛАУ. Однородные СЛАУ. Критерий существования ненулевого решения однородной СЛАУ. Свойства решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ, теорема о ее существовании. Нормальная фундаментальная система решений. Теорема о структуре общего решения однородной СЛАУ.
11
studfiles.net
Простейшие матричные уравнения
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒
Рассмотрим матрицы
; 
; 
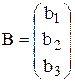Причем элементы матриц А и В заданы, а Х1, Х2, Х3 – неизвестные.
Тогда уравнение А × Х = В называется простейшим матричным уравнением.
Чтобы его решить, т.е. найти элементы матрицы неизвестных Х, поступим следующим образом:
1. Умножим обе части уравнения на матрицу А-1, обратную для матрицы А, слева:
А-1 (А × Х) = А-1 × В
2. Используя свойство умножения матриц, запишем
(А-1 × А) Х = А-1 × В
3. Из определения обратной матрицы
(А-1 × А = Е) имеем Е × Х = А-1 × В.
4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А-1 × В
Замечание. Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С-1справа.
Пример. Решить матричное уравнение
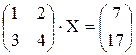
Решение. Введем обозначения
А = 
; В =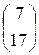 
,
Их определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид
Х = 
С учетом введенных обозначений имеем
А × Х = В откуда Х = А-1 × В
Найдем А-1 по алгоритму построения обратной матрицы
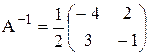
Вычислим произведение
Тогда для Х получим
Х = 
откуда х1 = 3, х2 = 2
Ранг матрицы
Рассмотрим матрицу А размера (m x n)
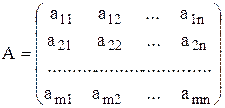
Минором к-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых К строк и любых К столбцов. Очевидно, к £ min (m, n).
Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.
Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором.
Определение. Матрицы, имеющие одинаковые ранги, называются эквивалентными.
Вычисление ранга матрицы
Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках.
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга:
- умножение всех элементов ряда матрицы на число l ¹ 0;
- замена строк столбцами и наоборот;
- перестановка местами параллельных рядов;
- вычеркивание нулевого ряда;
- прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.
Пример. Вычислить ранг матрицы
А =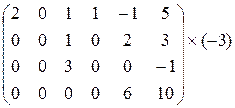 
Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (-3).
А ~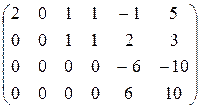 
К четвертой строке прибавим третью.
А ~ 
Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно r(А) = 3.
Системы n линейных уравнений с n неизвестными.
Методы их решения
Рассмотрим систему n линейных уравнений с n неизвестными.
а11х1 + а12х2 + … + а1nxn = b1
а21х1 + а22х2 + … + а2nxn = b2 (1)
……………………………….
аn1х1 + аn2х2 + … + аnnxn = bn
Определение: Решением системы (1) называется совокупность чисел (х1, х2, …, хn), которая обращает каждое уравнение системы в верное равенство.
Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1).
A =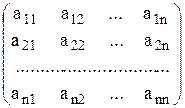 
Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей.
В =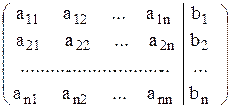 
Матричный метод
Рассмотрим матрицы
Х =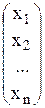 
- матрица неизвестных;
С =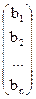 
- матрица свободных членов системы (1).
Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения
А × Х = С (2)
Решение уравнения (2) изложено выше, то есть Х = А-1 × С, где А-1 – обратная матрица для основной матрицы системы (1).
Метод Крамера
Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:
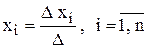
где D = det А – определитель основной матрицы А системы (1), который называется главным, Dхi получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т.е.
D =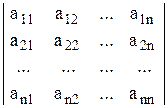 
;
Dх1 =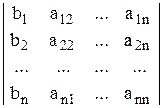 
;
Dх2 = 
; … ;
Dхn =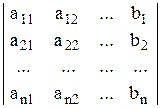 
;
Пример. Решить систему уравнений методом Крамера
2х1 + 3х2 + 4х3 = 15
х1 + х2 + 5х3 = 16
3х1 - 2х2 + х3 = 1
Решение.
Вычислим определитель основной матрицы системы
D = det A =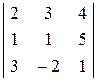 
= 44 ¹ 0
Вычислим вспомогательные определители
Dх1 =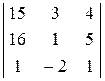 
= 0;
Dх2 = 
= 44;
Dх3 =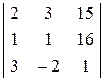 
= 132.
По формулам Крамера найдем неизвестные
; 
; 
.
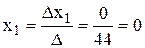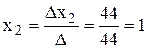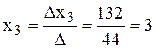Таким образом, х1 = 0; х2 = 1; х3 = 3.
Метод Гаусса
Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. в приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы и она приобретает также треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.
Пример. Решить систему уравнений методом Гаусса
3х1 + 2х2 + х3 = 17
2х1 - х2 + 2х3 = 8
х1 + 4х2 - 3х3 = 9
Решение. Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.
В =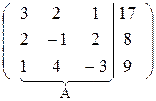 
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях
В ~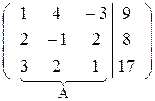 
Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:
В ~ 
После умножения второй строки на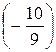 
и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:
В ~ 
Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим:
В ~ 
Восстановим из полученной матрицы В систему уравнений, равносильную данной
х1 + 4х2 - 3х3 = 9
х2 - 2х3 = 0
- 10х3 = -10
Из последнего уравнения находим 
Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2.
После подстановки х3 = 1 и х2 = 2 в первое уравнение для х1 получим х1 = 9 - 4х2 + 3х3 = 9 - 4 × 2 + 3 × 1 = 4.
Итак, х1 = 4, х2 = 2, х3 = 1.
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.
Проверка:
3 × 4 + 2 × 2 + 1 = 17 верно
2 × 4 - 2 + 2 × 1 = 8 верно
4 + 4 × 2 - 3 × 1 = 9 верно
Итак, система решена верно.
Читайте также:
lektsia.com
Матричные уравнения
Рассмотрим матричное уравнение вида
где \( A \) и \( B \) — данные матрицы, имеющие одинаковое количество строк, причем матрица \( A \) квадратная. Требуется найти матрицу \( X \) , удовлетворяющую уравнению (4.5).Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы \( A \) отличен от нуля, то матричное уравнение (4.5) имеет единственное решение \( X=A^{-1}B \) .
В самом деле, подставляя \( X=A^{-1}B \) в левую часть равенства (4.5), получаем \( A(A^{-1}B)=\underbrace{AA^{-1}}_{E}B=B \) , т.е. правую часть этого равенства.
Заметим, что решением матричного уравнения \( AX=E \) служит обратная матрица \( X=A^{-1} \) .
Рассмотрим также матричное уравнение вида
где \( A \) и \( B \) — данные матрицы, имеющие одинаковое количество столбцов, причем матрица \( A \) квадратная. Требуется найти матрицу \( Y \) , удовлетворяющую уравнению (4.6).Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы \( A \) отличен от нуля, то уравнение (4.6) имеет единственное решение \( Y=BA^{-1} \) .
Заметим, что матрица \( X \) является как бы "левым" частным от "деления" матрицы \( B \) на матрицу \( A \) , поскольку матрица \( X \) в (4.5) умножается на \( A \) слева, а матрица \( Y \) — "правым" частным, так как матрица \( Y \) в (4.6) умножается на \( A \) справа.
Пример 4.5. Даны матрицы
\( A=\begin{pmatrix}1&2\\1&4\end{pmatrix}\!,\quad B=\begin{pmatrix}1&3&5\\ 2&4&6 \end{pmatrix}\!,\quad C=\begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}\!. \)
Решить уравнения: а) \( AX=B \) ; б) \( YB=B \) ; в) \( YA=C \) .
Решение. Обратная матрица \( A^{-1}=\begin{pmatrix}2&-1\\ -1/2&1/2 \end{pmatrix} \) была найдена в примере 4.2.
а) Решение уравнения \( AX=B \) находим, умножая обе его части слева на \( A^{-1}: \)
\( X=A^{-1}B=\begin{pmatrix}2&-1\\-1/2&1/2\end{pmatrix}\!\cdot\! \begin{pmatrix} 1&3&5\\ 2&4&6\end{pmatrix}= \begin{pmatrix}0&2&4\\1/2&1/2&1/2\end{pmatrix}\!. \)
б) Уравнение не имеет решений, так как матрицы \( A \) и \( B \) имеют разное количество столбцов \( (2\ne3) \) .
в) Решение уравнения \( YA=C \) находим, умножая обе его части справа на \( A^{-1}: \)
\( Y=CA^{-1}= \begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}\!\cdot\! \begin{pmatrix}2&-1\\ -1/2&1/2 \end{pmatrix}= \begin{pmatrix}1&0\\4&-1\\7&-2\end{pmatrix}\!. \)
Пример 4.6. Решить уравнение: \( BX+2X=E \) , где \( B=\begin{pmatrix}-1&2\\1&2\end{pmatrix} \) .
Решение. Преобразуя левую часть уравнения:
\( B\cdot X+2\cdot X=B\cdot X+2\cdot E\cdot X=(B+2\cdot E)\cdot X, \)
приведем его к виду (4.1)\( A\cdot X=E, \) где \( A=B+2\cdot E=\begin{pmatrix}-1&2\\1&2\end{pmatrix}+ 2\cdot \begin{pmatrix}1&0\\0&1\end{pmatrix}=\begin{pmatrix}1&2\\1&4\end{pmatrix}\!. \)
Следовательно, \( X=A^{-1}E=A^{-1} \) . Обратная матрица найдена в примере 4.2:
\( A^{-1}=\begin{pmatrix}2&-1\\-1/2&1/2\end{pmatrix}\!. \) Значит, \( X=A^{-1}=\begin{pmatrix}2&-1\\-1/2&1/2\end{pmatrix}\!. \)
Пример 4.7. Решить уравнение \( AXB=C \) , где
\( A=\begin{pmatrix}1&2\\1&4\end{pmatrix}\!,\quad B=\begin{pmatrix}1&2&1\\ 0&1&0\\ 0&2&2\end{pmatrix}\!,\quad C=\begin{pmatrix}1&3&5\\2&4&6\end{pmatrix}\!. \)
Решение. Обратные матрицы
\( A^{-1}=\begin{pmatrix}2&-1\\-1/2&1/2\end{pmatrix}\!,\qquad B^{-1}=\begin{pmatrix}1&-1&-1/2\\ 0&1&0\\ 0&-1&1/2\end{pmatrix} \)
были найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по формуле\( \begin{aligned}X&=A^{-1}\cdot C\cdot B^{-1}= \begin{pmatrix}2&-1\\ -1/2&1/2 \end{pmatrix}\!\cdot\! \begin{pmatrix}1&3&5\\ 2&4&6\end{pmatrix}\!\cdot\! \begin{pmatrix}1&-1&-1/2\\ 0&1&0\\ 0&-1&1/2\end{pmatrix}=\\[2pt] &= \begin{pmatrix}0&2&4\\ 1/2&1/2&1/2\end{pmatrix}\!\cdot\! \begin{pmatrix} 1&-1&-1/2\\ 0&1&0\\ 0&-1&1/2\end{pmatrix}= \begin{pmatrix}0&-2&2\\ 1/2&-1/2& 0\end{pmatrix}\!.\end{aligned} \)
Пример 4.8. Решить уравнение \( AX=B \) , где
\( A=\begin{pmatrix}1&2\\2&4\end{pmatrix}\!,\qquad B=\begin{pmatrix}1&0\\ 2&0 \end{pmatrix}\!. \)
Решение. Определитель матрицы \( A \) равен нулю, следовательно, обратная матрица не существует. Поэтому нельзя использовать формулу \( X=A^{-1}B \) . Будем искать элементы матрицы \( X=\begin{pmatrix}a&b\\c&d\end{pmatrix} \) . Подставляя в уравнение, получаем
\( \begin{pmatrix}1&2\\2&4\end{pmatrix}\!\cdot\! \begin{pmatrix}a&b\\c&d\end{pmatrix}= \begin{pmatrix}1&0\\2&0\end{pmatrix}\!. \)
Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:
\( \begin{pmatrix} a+2c&b+2d\\ 2a+4c&2b+4d \end{pmatrix}= \begin{pmatrix}1&0\\2&0\end{pmatrix}\quad \Leftrightarrow\quad \begin{cases}a+2c=1,\\b+2d=0.\end{cases} \)
Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные \( a \) и \( b: \)
\( \begin{cases}a=1-2c,\\b=-2d.\end{cases} \)
Следовательно, решение матричного уравнения имеет вид
\( X=\begin{pmatrix}1-2c&-2d\\c&d\end{pmatrix}\!, \)
где параметры \( c \) и \( d \) могут принимать любые значения. Таким образом, данное матричное уравнение имеет бесконечное множество решений. В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Источник
calcsbox.com
Матричный калькулятор онлайн
Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень, умножить матрицу на число, сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a/b, где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.
Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы или очищать содержимое ячеек ).
Рис.1
При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.
Рис.2
Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку "A+B ","A-B" или "A×B".
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку "обратное ".
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку "определитель ".
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку "ранг ".
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "псевдообратное ".
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "полный ранг строк " или "полный ранг столбцов".
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "скелетное разложение ".
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку "решение AX=B".
Учтите, что матрицы и должны иметь равное количество строк .
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "Треугольный вид".
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
Для LU(LUP)-разложения:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "LU-разложение".
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "ядро (·)".
Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку "Ортогонализация Г.-Ш. (·)" или "Ортонормализация Г.-Ш. (·)".
matworld.ru
Матричные уравнения
Каталин Дэвид
AX = B, где матрица A обратима
Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^{-1}$.
$A^{-1}\cdot|A\cdot X = B$
$A^{-1}\cdot A\cdot X = A^{-1}\cdot B$
$I_{n}\cdot X = A^{-1}\cdot B$
Решение уравнения имеет общий вид$\color{red}{X =A^{-1}\cdot B}$
Пример 50Решить уравнение$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
Убедимся, что первая матрица обратима.$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.
Умножаем слева на обратную ей матрицу.$\begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}^{-1}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X= \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
$I_{2}\cdot X = \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
$X=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}= \begin{pmatrix} -9 & -22\\ 4 & 9 \end{pmatrix}$
XA = B, где матрица A обратима
Поскольку умножение матриц не всегда коммутативно, умножаем справа обе части уравнения на$ A^{-1}$.
$X\cdot A = B |\cdot A^{-1}$
$X\cdot A\cdot A^{-1} = B\cdot A^{-1}$
$X \cdot I_{n} =B\cdot A^{-1}$
Решение уравнения имеет общий вид$\color{red}{X =B\cdot A^{-1}}$
Пример 51Решить уравнение$X \begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}= \begin{pmatrix} 3 & 5\\ 2 & 1\\ \end{pmatrix}$
Убедимся, что первая матрица обратима.$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.
Умножаем справа на обратную ей матрицу.$X \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$
$X\cdot I_{2}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$
$X=\begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$
www.math10.com
