ГлавнаяРазноеШестикутна призма

Чотирикутна призма. Задачі з відповідями. Шестикутна призма


Правильна чотирикутна призма

Визначення.

Правильна чотирикутна призма - це шестигранник, підставами якого є два рівних квадрата, а бічні грані є рівні прямокутники

Бічне ребро - це загальна сторона двох суміжних бічних граней

Висота призми - це відрізок, перпендикулярний основам призми

Діагональ призми - відрізок, що з'єднує дві вершини основ, які не належать до однієї грані

Діагональна площина - площина, яка проходить через діагональ призми і її бічні ребра

Діагональний перетин - межа перетину призми і діагональної площині. Діагональний перетин правильної чотирикутної призми є прямокутником

Перпендикулярний перетин (ортогональний перетин) - це перетин призми і площини, проведеної перпендикулярно її бічним ребрам

Елементи правильної чотирикутної призми

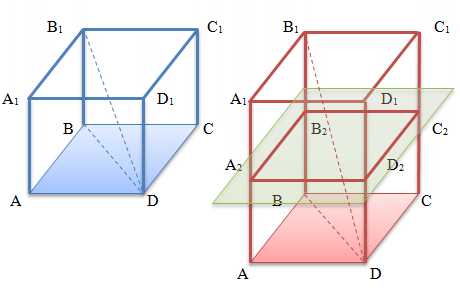
На малюнку зображено дві правильні чотирикутні призми, у яких позначені відповідними буквами:

Властивості правильної чотирикутної призми

Формули для правильної чотирикутної призми

Вказівки до вирішення завдань

При вирішенні завдань на тему "правильна чотирикутна призма" мається на увазі, що:

Правильна призма - призма в основі якої лежить правильний багатокутник, а бічні ребра перпендикулярні площинам основи. Тобто правильна чотирикутна призма містить в своєму основанні квадрат. (Див. вище "властивості правильної чотирикутної призми")

Примітка. Це частина уроку з завданнями по геометрії (розділ стереометрія - призма). Тут розміщені завдання, які викликають труднощі при вирішенні. Якщо Вам необхідно вирішити задачу з геометрії, якої тут немає - пишіть про це в форумі. Для позначення дії добування квадратного кореня в рішеннях задач використовується символ √ .   

Завдання

У правильної чотирикутної призмі площа основи 144 см2, а висота 14 см. Знайти діагональ призми і площу повної поверхні. 

Рішення. Правильний чотирикутник - це квадрат. Відповідно, сторона основи буде дорівнювати √144 = 12 см.  Звідки діагональ основи правильної прямокутної призми дорівнюватиме  √( 122 + 122 ) = √288 = 12√2 

Діагональ правильної призми утворює з діагоналлю основи і висотою призми прямокутний трикутник. Відповідно, по теоремі Піфагора діагональ заданої правильної чотирикутної призми дорівнюватиме √( ( 12√2 )2 + 142 ) = 22 см 

Відповідь: 22 см 

Завдання

Визначте повну поверхню правильної чотирикутної призми, якщо її діагональ дорівнює 5 см, а діагональ бічної грані дорівнюють 4 см.

Рішення. Оскільки в основі правильної чотирикутної призми лежить квадрат, то сторону основи (позначимо як a) знайдемо по теоремі Піфагора: 

a2 + a2 = 52  2a2 = 25  a = √12,5 

Висота бічної грані (позначимо як h) тоді буде дорівнювати: 

h3 + 12,5 = 42  h3 + 12,5 = 16  h3 = 3,5  h = √3,5 

Площа повної поверхні буде дорівнювати сумі площі бічної поверхні і подвоєної площі основи

S = 2a2 + 4ah  S = 25 + 4√12,5 * √3,5  S = 25 + 4√43,75  S = 25 + 4√(175/4)  S = 25 + 4√(7*25/4)  S = 25 + 10√7 ≈ 51,46 см2 . 

Відповідь: 25 + 10√7 ≈ 51,46 см2 .

 Призма. Паралелепіпед. Куб | Описание курса | Піраміда. Вирішення задач 

   

profmeter.com.ua

Чотирикутна призма. Задачі з відповідями

В інтернеті Ви можете зустріти безліч умов до задач на чотирикутну призму, однак не всі вони містять готові відповіді. Далі наведені готові розв'язки до посібника із ЗНО підготовки, які навчать вас знаходити площу повної поверхні призми, площу основи, об'єм, кути і т.д. Проаналізувавши відповіді, Ви можете пригадати потрібні формули та властивості призм. Приклади в першу чергу необхідні школярам 10-11 класів для покращення знань з геометрії, далі абітурієнтам для підготовки до вступу у ВУЗи, а також батькам для перевірки правильності обчислень їх дітей та вчителям для підготовки уроків. Нові малюнки до завдань допоможуть Вам швидко розібратися з обчисленнями.

Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж 

Тема 36.4 Чотирикутна призма

Задача 36.9 Знайти площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює a, а висота – H.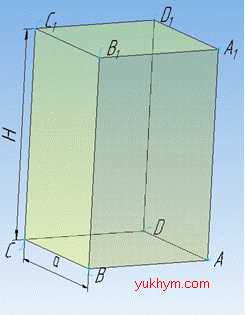

Розв'язання: Площа повної поверхні правильної призми:Sn=2Soc+Sb.В основі правильної чотирикутної призми лежить квадрат зі стороною a. Тому площа основи:Soc=a2,периметр основи:Poc=4a.Площа бічної поверхні:Sb=Soc•H=4aH.Площа повної поверхні правильної чотирикутної призми: Sn=2Soc+Sb=2a2+4aH=2a(a+2H).Відповідь: 2a(a+2H) – Д.

 

Задача 36.10 В основі прямої призми лежить рівнобічна трапеція з основами 4 см і 10 см і бічною стороною 5 см. Бічне ребро призми дорівнює 10 см. Обчислити повну поверхню призми. Розв'язання: Площа повної поверхні прямої призми: Sп=2Soc+Sb. В основі прямої призми лежить рівнобічна трапеція з основами AD=4 см і BC=10 см і бічною стороною AB=CD=5 см.Знайдемо висоту DL трапеції. Із прямокутного трикутника DLC (∠DLC=90, бо DL⊥BC, CD=5 см – гіпотенуза і CL=3 см – катет) знайдемо катет DL. DL2=CD2-CL2, звідси Площа основи – трапеції ABCD: Периметр основи: Poc=AB+BC+CD=2•5+10+4=24 см. Площа бічної поверхні:Sб=Poc•h=24•10=240 см2.Площа повної поверхні прямої призми:Sп=2Soc+Sb=2•28+240=296 см2. Відповідь: 296 см2 – Д.

 

 

Задача 36.16 Діагональ правильної чотирикутної призми дорівнює 13 см, а діагональ бічної грані дорівнює 12 см. Знайти площу основи призми. Розв'язання: В основі правильної чотирикутної призми лежить квадрат зі стороною a, тому площу основи обчислимо за формулою:Soc=a2. У правильної призми бічне ребро перпендикулярне до площини основи CC1⊥ (ABC), тому CC1⊥BC. Звідси CC – перпендикуляр опущений з вершини C1 на площину основи (на квадрат ABCD), BC1 – похила, яка опущена з цієї ж вершини C1 на площину основи, BC – проекція похилої BC1.Оскільки основа – квадрат ABCD, то AB⊥BC. За теоремою «Про три перпендикуляри» маємо AB⊥BC1, тому ΔABC1 – прямокутний (∠ABC1=90). З прямокутного трикутника ABC1 (∠ABC1=90), в якому BC<1=12 см – катет (діагональ бічної грані) і AC1=13 см – гіпотенуза (діагональ призми), за теоремою Піфагора знайдемо катет AB=a – довжину сторони квадрата: Площа основи правильної чотирикутної призми – квадрата ABCD: Soc=a2=52=25 см2. Відповідь: 25 см2 – Б.

 

Задача 36.17 У правильній чотирикутній призмі площа діагонального перерізу дорівнює S. Визначити площу бічної поверхні.

Розв'язання: Площа бічної поверхні правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:Sб=Poc•H=4aH.У правильній чотирикутній призмі діагональним перерізом є прямокутник ACC1A1 зі сторонами діагоналі основи призми AC і висоти CC1=H. Діагональ основи правильної чотирикутної призми (квадрата ABCD): (Обчислюємо як довжину гіпотенузи AС прямокутного ΔABC (∠ABC=90)). Площа діагонального перерізу: Площа бічної поверхні правильної чотирикутної призми: Відповідь: 2√2S – В.

 

Задача 36.18 Діагональним перерізом правильної чотирикутної призми є квадрат, площа якого дорівнює S. Визначити об'єм призми. Розв'язання: Об'єм правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою: За умовою задачі у правильній чотирикутній призмі діагональним перерізом є квадрат ACC1A1 зі стороною діагоналі основи призми AC. Діагональ основи правильної чотирикутної призми (квадрата ABCD): (Обчислюємо як довжину гіпотенузи AC прямокутного ΔABC). Площа діагонального перерізу: звідси отримаємо Оскільки ACC1A1 – квадрат, то Об'єм правильної чотирикутної призми: Відповідь: S√S/2 – Д.

 

Задача 36.20 Бічна поверхня правильної чотирикутної призми дорівнює Q, а її об'єм – V. Визначити сторону основи призми. Розв'язання: В основі правильної чотирикутної призми лежить квадрат зі стороною a. Об'єм правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:V=Soc•H=a2•H. Бічна поверхня (площа бічної поверхні) правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою: Sб=Pос•H=4aH. За умовою задачі Складемо відношення звідси отримаємо a=4V/Q.Відповідь: 4V/Q – Д.

 

Задача 36.21 Розгорткою бічної поверхні правильної чотирикутної призми є квадрат зі стороною 8 дм. Знайти об'єм призми. Розв'язання: Об'єм правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:V=Soc•H=a2•H. В основі правильної чотирикутної призми лежить квадрат ABCD зі стороною a. Оскільки розгорткою призми є квадрат зі стороною 8 дм, то висота призми дорівнює периметру основи призми: H=Poc=8 дм. Периметр квадрата: Poc=4a=8 дм, звідси a=2 дм – довжина сторони основи. Об'єм правильної чотирикутної призми:  Відповідь: 32 дм3 – В.

 

Задача 36.24 Установити відповідність між площами діагональних перерізів (1–4), які є квадратами у правильних чотирикутних призм, та об'ємами цих призм (А–Д). Розв'язання: (Розв'язок цієї задачі дивись у номері 36.18.) Обчислимо об'єм призми для кожного випадку:1) S=64 м2, тоді Г; 2) S=16 см2, тоді А; 3) S=36 см2, тоді В; 4) S=4 см2, тоді Д.

 

Задача 36.26 Діагональ правильної чотирикутної призми утворює з площиною основи кут 450. Знайти у градусах кут, утворений цією діагоналлю з площиною бічної грані. Розв'язання: У правильної призми бічне ребро (висота) перпендикулярна до площини основи (квадрата ABCD), тому бічне ребро перпендикулярне до кожного відрізка, що лежить в площині основи, тобто CC1⊥AC, CC1⊥BC. Так як CC1⊥AC, то відрізок AC (діагональ квадрата) є ортогональною проекцією діагоналі призми AC1, тому ∠C1AC=45 – кут між діагоналлю призми і площиною основи і ΔC1AC – прямокутний (∠ACC1=90). Нехай сторона основи правильної чотирикутної призми дорівнює a. Оскільки в основі призми лежить квадрат, то за теоремою Піфагора у прямокутному ΔABC (∠ABC=90) маємо Розглянемо прямокутний трикутник C1AC, у якого ∠ACC1=90 і ∠C1AC=45. За теоремою про суму кутів трикутника, маємо ∠CC1A=180-(90+45)=45. Звідси слідує, що ΔC1AC – рівнобедрений з основою AC1 і бічними сторонами AC=CC1=a√2. За теоремою Піфагора обчислимо довжину діагоналі призми AC1: Відрізок CC1 – перпендикуляр опущений з вершини C1 на площину основи (на квадрат ABCD), BC1 – похила, яка опущена з цієї ж вершини C1 на площину основи, BC – проекція похилої BC1. Оскільки основа – квадрат ABCD, то AB⊥BC. За теоремою «Про три перпендикуляри» маємо AB⊥BC1, тому ΔABC1 – прямокутний (∠ABC1=90), а – кут між діагоналлю призми AC1 з площиною бічної грані BB1C1C, оскільки відрізок BC1 – ортогональна проекція відрізка AC1 на площину бічної грані BB1C1C. Розглянемо прямокутний трикутник ABC1, у якого ∠ABC1=90, AC1=2a – гіпотенуза, і AB=a – протилежний катет до кута За означенням синуса гострого кута у прямокутного трикутника маємо звідси слідує, що Відповідь: 300.

 

Задача 36.34 Висота правильної чотирикутної призми дорівнює 5, а кут між діагоналями, проведеними з однієї вершини основи у двох суміжних бічних гранях, – 600. Визначити площу бічної поверхні призми. 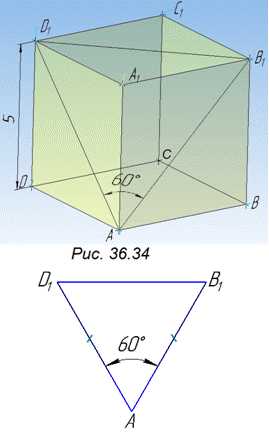Розв'язання: Площу бічної поверхні правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою: Sb=Poc•H=4a•5=20a, де H=AA1=BB1=CC1=DD1=5 – висота правильної чотирикутної призми; a=AB=BC=CD=AD – сторона основи правильної чотирикутної призми.Нехай ∠BAD1 – кут між діагоналями AB1 і AD1 двох суміжних бічних граней AA1B1B і AA1D1D відповідно. Проведемо відрізок B1D1 (діагональ грані A1B1C1D1) і розглянемо трикутник B1A1D1. Оскільки в умові задана правильна чотирикутна призма, то в основі лежать квадрати, а бічні грані є рівними прямокутниками. У рівних прямокутників всі діагоналі рівні, тому AB1=AD1. Отже, ΔB1AD1 – рівнобедрений з основою B1D1 і (за властивістю) Трикутник, у якого всі кути рівні (∠AB1D1=∠AD1B1=∠B1AD1=60) – рівносторонній: AB1=AD1=B1D1. Правильна чотирикутна призма, у якої всі діагоналі граней рівні (а відповідно, і всі ребра рівні) називається кубом. Тому довжина ребра куба: a=H=5. Площа бічної поверхні правильної чотирикутної призми (куба):Sb=Poc•H=20•5=100Відповідь: 100.

На наступному уроці розберемо складніші приклади на похилі трикутні та чотирикутні піраміди, а далі перейдемо до пірамід.  Всім школярам, для яких ця тема здається важкою рекомендуємо переглянути попередні простіші статті на паралелепіпеди та куби.

yukhym.com

Как сделать призму из бумаги?

В основе геометрического тела – призмы лежат многоугольники, а каждая боковая грань – параллелограмм. Непосвященный, возможно, немного испугался. Но если вашего ребенка просят прийти на урок с призмой, вы, естественно, захотите помочь ему и объяснить, как сделать призму из бумаги.

Начнем с изготовления прямой призмы. В этой призме боковые ребра перпендикулярны основаниям. Наиболее проста в изготовлении своими руками призма из бумаги с тремя гранями, так как в ее основаниях лежат простейшие из многоугольников – треугольники. Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.

Треугольная призма

Продумаем, какая по высоте будет наша треугольная призма из бумаги. Начертим прямоугольник-с одной стороной, равной высоте, а другой - равной длине периметру треугольника в основании. Полученный прямоугольник разделим параллельными прямыми на три равные части. От углов прямоугольника, находящегося в середине, циркулем проведем окружности с радиусом, равным стороне нашего треугольника в основании. Где окружности пересекутся за пределами первоначального прямоугольника, поставим точки и соединим их с центрами окружностей. Мы должны получить фигуру, изображенную в середине рисунка.

Далее фигуру вырезаем с небольшими припусками для склеивания, сгибаем по имеющимся прямым линиям и получаем готовую призму.

По какому шаблону изготавливается призма из бумаги с четырьмя гранями, наглядно демонстрирует схема на рисунке.

Шестиугольная призма

Пример заготовки для пятигранной призмы представлен на рисунке.

Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник. Наклонная призма

Наклонная призма из бумаги представлена на этом рисунке.

Ее боковые грани находятся под углом к основанию. Такую призму можно изготовить по шаблону-развертке. Освоив изготовление призмы, можно приступать к следующим геометрическим фигурами: пирамиде, параллелепипеду и более сложному икосаэдру из бумаги.

 

womanadvice.ru

Шестиугольная призма — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

В геометрии шестиугольная призма — это призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин[1].

До заточки многие карандаши имеют форму длинной шестиугольной призмы[2].

Полуправильный (или однородный) многогранник

Если все боковые грани одинаковые, шестиугольная призма является полуправильным многогранником, более обще, однородным многогранником[en] и четвёртой призмой в бесконечном множестве призм, образованных прямоугольными боковыми сторонами и двумя правильными основаниями. Призму можно рассматривать как усечённый[en] шестигранный осоэдр, представленный символом Шлефли t{2,6}. С другой стороны, его можно рассматривать как прямое произведение правильного шестиугольника на отрезок, которое представляется как {6}×{}. Двойственным многогранником шестиугольной призмы является шестиугольная бипирамида[en].

Группой симметрии прямой шестиугольной призмы является D6h с порядком 24, а группой вращений является D6 с порядком 12.

Объём

Как и у большинства призм, объём правильной шестигранной призмы можно найти умножением площади основания (с длиной стороны <math>a</math>) на высоту <math>h</math>, что даёт формулу[3]:

<math>V = \frac{3 \sqrt{3}}{2}a^2 \times h</math>

Симметрия

Топология однородной шестиугольной призмы могут иметь геометрические вариации с низкой симметрией:

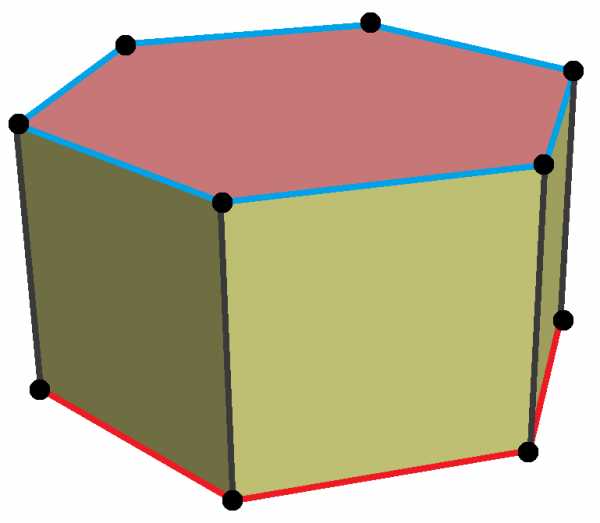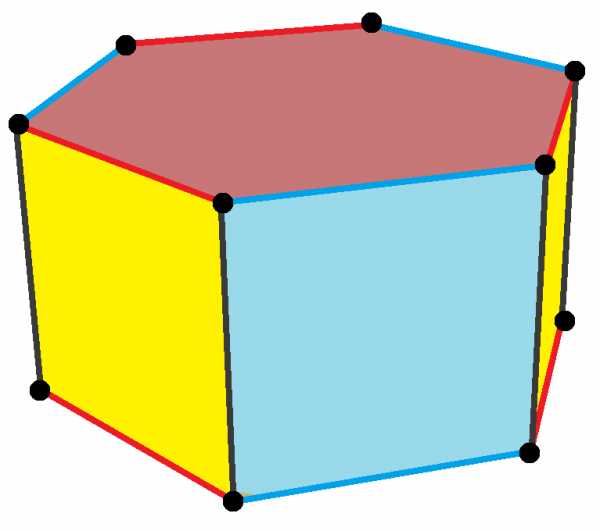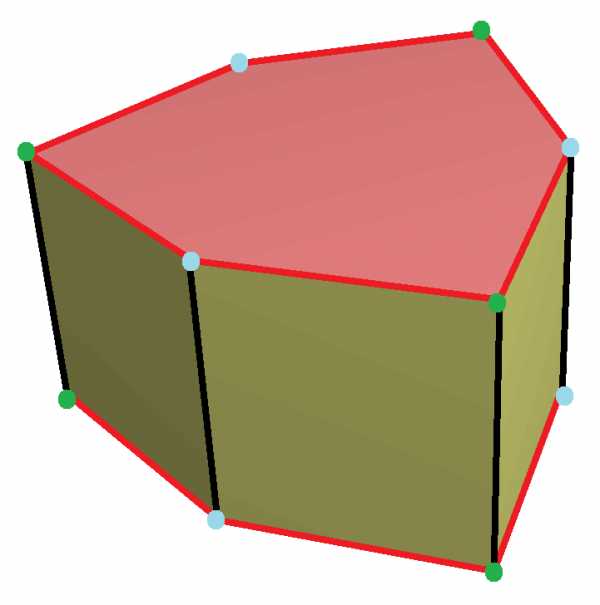Симметрия[en] D6h, [2,6], (*622) C6v, [6], (*66) D3h, [2,3], (*322) D3d, [2+,6], (2*3) Конструкция {6}×{}, t{3}×{}, s2{2,6}, Рисунок Нарушение

Как часть пространственных мозаик

Шестигранная призма присутствует как ячейка в четырёх призматических однородных выпуклых сотах[en] в трёхмерном пространстве:

Шестигранные призмы существуют также в качестве трёхмерных граней четырёхмерных однородных многогранников[en]:

Связанные многогранники и мозаики

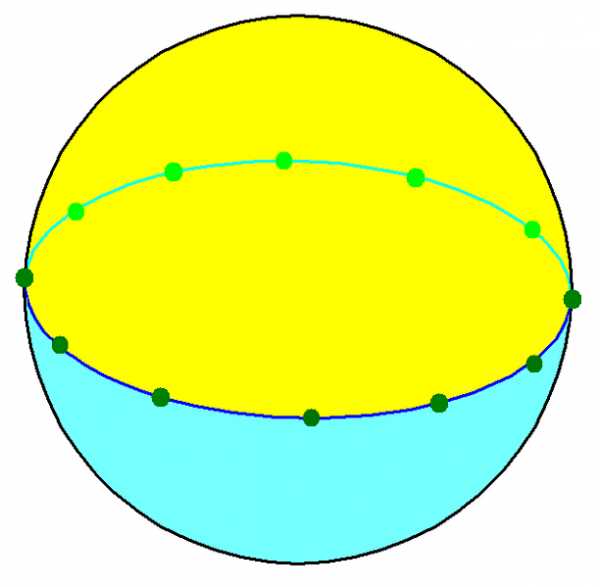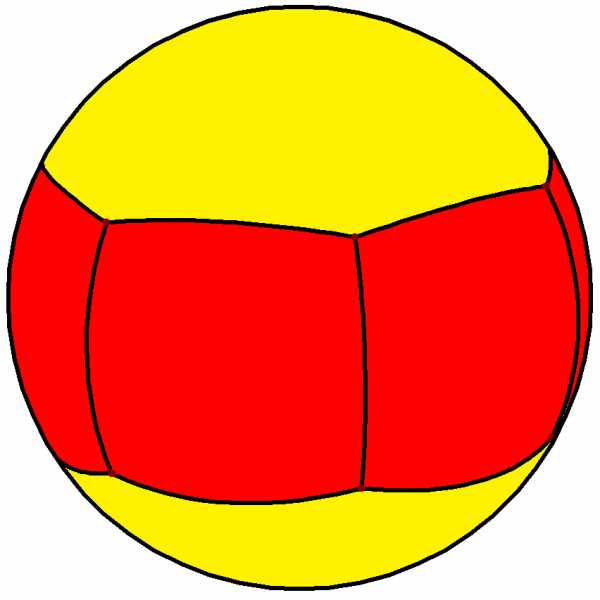Однородные шестиугольные диэдральные сферические многогранники Симметрия[en]|: [6,2], (*622) [6,2]+, (622) [6,2+], (2*3) Двойственные им многогранники
{6,2} t{6,2} r{6,2} t{2,6} {2,6} rr{2,6} tr{6,2}[en] sr{6,2} s{2,6}
V62 V122 V62 V4.4.6[en] V26 V4.4.6[en] V4.4.12 V3.3.3.6[en] V3.3.3.3

Этот многогранник можно считать членом последовательности однородных многогранников с угловой фигурой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 членами последовательности являются усечённые во всех углах многогранники (зоноэдры), и они показаны ниже как сферические мозаики. Для p > 6 они являются мозаиками гиперболической плоскости начиная с усечённой трисемиугольной мозаики[en].

*n32 мутации по симметрии полностью усечённых мозаик: 4.6.2n Симметрия*n32[en]n,3[en] Сферическая[en] Евклидова Компактная гиперболическая Паракомп. Некомпактная гиперболическая *232[2,3] *332[3,3] *432[4,3] *532[5,3] *632[6,3] *732[7,3] *832[8,3] *∞32[∞,3]  [12i,3]  [9i,3]  [6i,3]  [3i,3] Фигуры Конфигурация Двойственная Конфигурация[en]
4.6.4 4.6.6 4.6.8 4.6.10 4.6.12[en] 4.6.14[en] 4.6.16[en] 4.6.∞[en] 4.6.24i 4.6.18i 4.6.12i 4.6.6i
V4.6.4[en] V4.6.6 V4.6.8[en] V4.6.10 V4.6.12[en] V4.6.14[en] V4.6.16[en] V4.6.∞ V4.6.24i V4.6.18i V4.6.12i V4.6.6i

Смотрите также

Напишите отзыв о статье "Шестиугольная призма"

Примечания

  1. ↑ 1 2 Anthony Pugh. [books.google.com/books?id=IDDxpYQTR7kC&pg=PA21 Polyhedra: A Visual Approach]. — University of California Press, 1976. — С. 21, 27, 62. — ISBN 9780520030565.
  2. ↑ Audrey Simpson. [books.google.com/books?id=Xm80FfQZ42AC&pg=PA266 Core Mathematics for Cambridge IGCSE]. — Cambridge University Press, 2011. — С. 266–267. — ISBN 9780521727921.
  3. ↑ Carolyn C. Wheater. [books.google.com/books?id=hxSx6ySgdq0C&pg=PA236 Geometry]. — Career Press, 2007. — С. 236–237. — ISBN 9781564149367.

Ссылки

Отрывок, характеризующий Шестиугольная призма

– Да, да, – сказал Пьер. Но адъютант, повернув лошадь, ехал дальше. – Здесь то слава богу, – сказал адъютант, – но на левом фланге у Багратиона ужасная жарня идет. – Неужели? – спросил Пьер. – Это где же? – Да вот поедемте со мной на курган, от нас видно. А у нас на батарее еще сносно, – сказал адъютант. – Что ж, едете? – Да, я с вами, – сказал Пьер, глядя вокруг себя и отыскивая глазами своего берейтора. Тут только в первый раз Пьер увидал раненых, бредущих пешком и несомых на носилках. На том самом лужке с пахучими рядами сена, по которому он проезжал вчера, поперек рядов, неловко подвернув голову, неподвижно лежал один солдат с свалившимся кивером. – А этого отчего не подняли? – начал было Пьер; но, увидав строгое лицо адъютанта, оглянувшегося в ту же сторону, он замолчал. Пьер не нашел своего берейтора и вместе с адъютантом низом поехал по лощине к кургану Раевского. Лошадь Пьера отставала от адъютанта и равномерно встряхивала его. – Вы, видно, не привыкли верхом ездить, граф? – спросил адъютант. – Нет, ничего, но что то она прыгает очень, – с недоуменьем сказал Пьер. – Ээ!.. да она ранена, – сказал адъютант, – правая передняя, выше колена. Пуля, должно быть. Поздравляю, граф, – сказал он, – le bapteme de feu [крещение огнем]. Проехав в дыму по шестому корпусу, позади артиллерии, которая, выдвинутая вперед, стреляла, оглушая своими выстрелами, они приехали к небольшому лесу. В лесу было прохладно, тихо и пахло осенью. Пьер и адъютант слезли с лошадей и пешком вошли на гору. – Здесь генерал? – спросил адъютант, подходя к кургану. – Сейчас были, поехали сюда, – указывая вправо, отвечали ему. Адъютант оглянулся на Пьера, как бы не зная, что ему теперь с ним делать. – Не беспокойтесь, – сказал Пьер. – Я пойду на курган, можно? – Да пойдите, оттуда все видно и не так опасно. А я заеду за вами. Пьер пошел на батарею, и адъютант поехал дальше. Больше они не видались, и уже гораздо после Пьер узнал, что этому адъютанту в этот день оторвало руку. Курган, на который вошел Пьер, был то знаменитое (потом известное у русских под именем курганной батареи, или батареи Раевского, а у французов под именем la grande redoute, la fatale redoute, la redoute du centre [большого редута, рокового редута, центрального редута] место, вокруг которого положены десятки тысяч людей и которое французы считали важнейшим пунктом позиции. Редут этот состоял из кургана, на котором с трех сторон были выкопаны канавы. В окопанном канавами место стояли десять стрелявших пушек, высунутых в отверстие валов. В линию с курганом стояли с обеих сторон пушки, тоже беспрестанно стрелявшие. Немного позади пушек стояли пехотные войска. Входя на этот курган, Пьер никак не думал, что это окопанное небольшими канавами место, на котором стояло и стреляло несколько пушек, было самое важное место в сражении. Пьеру, напротив, казалось, что это место (именно потому, что он находился на нем) было одно из самых незначительных мест сражения. Войдя на курган, Пьер сел в конце канавы, окружающей батарею, и с бессознательно радостной улыбкой смотрел на то, что делалось вокруг него. Изредка Пьер все с той же улыбкой вставал и, стараясь не помешать солдатам, заряжавшим и накатывавшим орудия, беспрестанно пробегавшим мимо него с сумками и зарядами, прохаживался по батарее. Пушки с этой батареи беспрестанно одна за другой стреляли, оглушая своими звуками и застилая всю окрестность пороховым дымом. В противность той жуткости, которая чувствовалась между пехотными солдатами прикрытия, здесь, на батарее, где небольшое количество людей, занятых делом, бело ограничено, отделено от других канавой, – здесь чувствовалось одинаковое и общее всем, как бы семейное оживление. Появление невоенной фигуры Пьера в белой шляпе сначала неприятно поразило этих людей. Солдаты, проходя мимо его, удивленно и даже испуганно косились на его фигуру. Старший артиллерийский офицер, высокий, с длинными ногами, рябой человек, как будто для того, чтобы посмотреть на действие крайнего орудия, подошел к Пьеру и любопытно посмотрел на него. Молоденький круглолицый офицерик, еще совершенный ребенок, очевидно, только что выпущенный из корпуса, распоряжаясь весьма старательно порученными ему двумя пушками, строго обратился к Пьеру. – Господин, позвольте вас попросить с дороги, – сказал он ему, – здесь нельзя. Солдаты неодобрительно покачивали головами, глядя на Пьера. Но когда все убедились, что этот человек в белой шляпе не только не делал ничего дурного, но или смирно сидел на откосе вала, или с робкой улыбкой, учтиво сторонясь перед солдатами, прохаживался по батарее под выстрелами так же спокойно, как по бульвару, тогда понемногу чувство недоброжелательного недоуменья к нему стало переходить в ласковое и шутливое участие, подобное тому, которое солдаты имеют к своим животным: собакам, петухам, козлам и вообще животным, живущим при воинских командах. Солдаты эти сейчас же мысленно приняли Пьера в свою семью, присвоили себе и дали ему прозвище. «Наш барин» прозвали его и про него ласково смеялись между собой. Одно ядро взрыло землю в двух шагах от Пьера. Он, обчищая взбрызнутую ядром землю с платья, с улыбкой оглянулся вокруг себя. – И как это вы не боитесь, барин, право! – обратился к Пьеру краснорожий широкий солдат, оскаливая крепкие белые зубы. – А ты разве боишься? – спросил Пьер. – А то как же? – отвечал солдат. – Ведь она не помилует. Она шмякнет, так кишки вон. Нельзя не бояться, – сказал он, смеясь. Несколько солдат с веселыми и ласковыми лицами остановились подле Пьера. Они как будто не ожидали того, чтобы он говорил, как все, и это открытие обрадовало их. – Наше дело солдатское. А вот барин, так удивительно. Вот так барин! – По местам! – крикнул молоденький офицер на собравшихся вокруг Пьера солдат. Молоденький офицер этот, видимо, исполнял свою должность в первый или во второй раз и потому с особенной отчетливостью и форменностью обращался и с солдатами и с начальником.

wiki-org.ru

Линейно-конструктивный рисунок шестигранной призмы | СПЛАЙН

Главное меню » Чертёж и рисунок » Архитектурный рисунок по представлению » Линейно-конструктивный рисунок шестигранной призмы

Научимся изображать шестигранную призму в различных положениях.

Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани – одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 – 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 – 1 и 4 – 3 параллельны прямой 5 – 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.

На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.

Линейно-конструктивный рисунок шес

hspline.com

П ятикутна призма

Правильна п'ятикутна призма описана навколо кулі – GeoGebra Net of Solid Shapes - Pentagonal Prism / П'ятикутна призма Восьмикутна призма: Трикутна піраміда: Чотирикутна піраміда П’ятикутна піраміда · Файл DOC · Переглянути в Інтернеті Комбінації геометричних тіл - mir-inf Тривалість відео: 2 хв Переглядів: 39 тис c1 d1 Наприклад: b1 f1 abcdfa1b1c1d1f1- a1 п’ятикутна призма bd1 і fc1-діагоналі призми f1h-висота призми c d b f h a Контрольна робота з геометрії на тему "Многогранники" з Скільки граней має п'ятикутна призма? - Школьные Знанияcom · Файл DOC · Переглянути в Інтернеті Calaméo - Збірник завдань ДПА з математики 2014 Правильна п’ятикутна призма, до-вжина сторони основи якої дорів-нює 15 мм, а висота – 55 мм Варіант 8 Циліндр, радіус основи якого до-рівнює 18 мм, а висота – 40 мм 12 Самостійна робота з геометрії для учнів 10 класу на тему "Вступ до стереометрії" Похила призма – це призма, в якої бічні ребра не перпендикулярні до основ Правильна призма – це пряма призма, основами якої є правильні многокутники Об'єм і · righ.tekhnologiya-prodazh.ru
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
    •     PR.RU™  Contacts: [email protected]

    mue.megarulez.ru

    Шестиугольная призма — Википедия

    Материал из Википедии — свободной энциклопедии

    В геометрии шестиугольная призма — это призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин[1].

    До заточки многие карандаши имеют форму длинной шестиугольной призмы[2].

    Полуправильный (или однородный) многогранник

    Если все боковые грани одинаковые, шестиугольная призма является полуправильным многогранником, более обще, однородным многогранником[en] и четвёртой призмой в бесконечном множестве призм, образованных прямоугольными боковыми сторонами и двумя правильными основаниями. Призму можно рассматривать как усечённый[en] шестигранный осоэдр, представленный символом Шлефли t{2,6}. С другой стороны, его можно рассматривать как прямое произведение правильного шестиугольника на отрезок, которое представляется как {6}×{}. Двойственным многогранником шестиугольной призмы является шестиугольная бипирамида[en].

    Группой симметрии прямой шестиугольной призмы является D6h с порядком 24, а группой вращений является D6 с порядком 12.

    Видео по теме

    Объём

    Как и у большинства призм, объём правильной шестигранной призмы можно найти умножением площади основания (с длиной стороны a{\displaystyle a}) на высоту h{\displaystyle h}, что даёт формулу[3]:

    V=332a2×h{\displaystyle V={\frac {3{\sqrt {3}}}{2}}a^{2}\times h}

    Симметрия

    Топология однородной шестиугольной призмы могут иметь геометрические вариации с низкой симметрией:

    Симметрия[en]* D6h, [2,6], (*622) C6v, [6], (*66) D3h, [2,3], (*322) D3d, [2+,6], (2*3) Конструкция {6}×{}, t{3}×{}, s2{2,6}, Рисунок Нарушение

    Как часть пространственных мозаик

    Шестигранная призма присутствует как ячейка в четырёх призматических однородных выпуклых сотах[en] в трёхмерном пространстве:

    Шестигранные призмы существуют также в качестве трёхмерных граней четырёхмерных однородных многогранников[en]:

    Связанные многогранники и мозаики

    Однородные шестиугольные диэдральные сферические многогранники Симметрия|: [6,2], (*622) [6,2]+, (622) [6,2+], (2*3) Двойственные им многогранники
    {6,2} t{6,2} r{6,2} t{2,6} {2,6} rr{2,6} tr{6,2}[en] sr{6,2} s{2,6}
    V62 V122 V62 V4.4.6[en] V26 V4.4.6[en] V4.4.12 V3.3.3.6[en] V3.3.3.3

    Этот многогранник можно считать членом последовательности однородных многогранников с угловой фигурой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 членами последовательности являются усечённые во всех углах многогранники (зоноэдры), и они показаны ниже как сферические мозаики. Для p > 6 они являются мозаиками гиперболической плоскости начиная с усечённой трисемиугольной мозаики[en].

    *n32 мутации по симметрии полностью усечённых мозаик: 4.6.2n Симметрия*n32[en]n,3[en] Сферическая[en]* Евклидова Компактная гиперболическая Паракомп. Некомпактная гиперболическая *232[2,3] *332[3,3] *432[4,3] *532[5,3] *632[6,3] *732[7,3] *832[8,3] *∞32[∞,3]  [12i,3]  [9i,3]  [6i,3]  [3i,3] Фигуры Конфигурация Двойственная Конфигурация[en]*
    4.6.4 4.6.6 4.6.8 4.6.10 4.6.12[en] 4.6.14[en] 4.6.16[en] 4.6.∞[en] 4.6.24i 4.6.18i 4.6.12i 4.6.6i
    V4.6.4[en] V4.6.6 V4.6.8[en] V4.6.10 V4.6.12[en] V4.6.14[en] V4.6.16[en] V4.6.∞ V4.6.24i V4.6.18i V4.6.12i V4.6.6i

    Смотрите также

    Примечания

    Ссылки

    wikipedia.green