2.1.8 Простейшие системы уравнений с двумя неизвестными. Системы 2 уравнений с 2 неизвестными
Способы решения систем уравнений с двумя неизвестными
Линейные системы уравнений
Системы линейных уравнений. Метод подстановки+ показать
• Выражаем одну переменную через другую.
• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.
• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.
Решить систему уравнений: 
Решение: + показать
Системы линейных уравнений. Метод сложения+ показать
• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.
• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной.
• Решаем полученное уравнение с одной неизвестной.
• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.
1. Решить систему уравнений:
Решение: + показать
Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.
Ответ: 
2. Решить систему уравнений: 
Решение: + показать
Нелинейные системы уравнений
Системы уравнений, сводящихся к линейным1. Решить систему уравнений: 
Решение: + показать
Можно сделать замену 
Тогда выходим на систему линейных уравнений: 
Систему можно решить методом сложения, например.
Но приведем решение без замены.
Умножим первое уравнение системы на 
, второе – на 
и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.
Ответ: 
2. Решить систему уравнений: 
Решение: + показать
Можно сделать замену 
и выйти на систему линейных уравнений:
Приведем решение без замены.
Выражаем 
из второго уравнения системы и подставляем в первое.
Ответ: 
Решить систему уравнений: 
Решение: + показать
Выражаем 
из первого уравнения системы и подставляем во второе.
Ответ: 
Решить систему уравнений: 
Решение: + показать
Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.
Ответ: 
1. Решить систему уравнений: 
Решение: + показать
Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений.
Ответ: 
Симметрические системы. Метод введения переменной
Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных 
и – уравнение, которое не изменяется при замене на и на .
Для таких систем удобно использовать замену 
Решить систему уравнений: 
Решение: + показать
При замене 
приходим к следующей системе
которую будем решать способом подстановки:
Производим обратную замену:
Ответ: 
Системы однородных уравнений и приводящиеся к ним системы
Однородным уравнением с двумя неизвестными 
будем называть уравнение вида 
1. Решить систему уравнений: 
Решение: + показать
2. Решить систему уравнений: 
Решение: + показать
Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.
Ответ: 
Графический метод решения систем уравнений
1. Решите графически систему уравнений: 
Решение: + показать
Выразим в обеих строках системы через :
Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.
Ответ: 
2. Решите графически систему уравнений: 
Решение: + показать
3. Решите графически систему уравнений: 
Решение: + показать
——————————————————————————————————
Задания для самостоятельной работы
+ показать
Решите системы уравнений:
1. 
Ответ:
2. 
Ответ: 
3. 
Ответ: 
4. 
Ответ: 
5. 
Ответ: 
6. 
Ответ: 
7. 
Ответ:
8. 
Ответ: 
Решите графически системы уравнений:
9. 
Ответ: 
10. 
Ответ: 
egemaximum.ru
Методы решения систем уравнений с двумя неизвестными
Поиск Лекций1. Графический
Можно построить 2 графика, соответствующие данным уравнениям и найти координаты точек пересечения.
Минус этого метода в том, что точки пересечения могут быть не в целых координатах, и по графику точные значения чисел х и у сложно определить.
2. Метод подстановки
Алгоритм:
1) Выразить одну переменную через другую из одного уравнения системы.
2) Подставить полученное выражение в другое уравнение системы.
3) Решить полученное уравнение.
4) Найти соответствующее значение другой переменной.
5) Записать ответ в виде пар значений (х; у).
Пример:
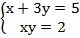
х = 5 - 3у - выразили х через у из первого уравнения системы
(5 - 3у) · у = 2 -подставили полученное выражение вместо х во второе уравнение
5у – 3у2 = 2- раскрыли скобки
3у2 – 5у + 2 = 0 - перенесли все слагаемые в одну часть
D = 25 - 4·3·2= 25 – 24 = 1 - вычислили дискриминант
у1 = (5+1):6 = 1; у2 = (5-1):6 = 
- нашли корни уравнения
Подставляем поочередно каждое из найденных значений у в выражение х = 5 - 3у
х1 = 5 – 3·1 = 2; х2 = 5 – 3· 
= 3
Ответ: (2; 1), (3; )- не забываем, что сначала записывается х, потом у.
3. Метод алгебраического сложения
Суть метода в том, чтобы путем сложения избавиться от одной из переменных. Для этого перед данной переменной нужно иметь в обоих уравнениях противоположные коэффициенты.
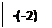Пример:
– 6у – у = – 10 + 2
–7у = –8
у =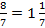 
2х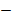 
= 2
2х = 2
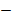
2х = 
х = 
Ответ: 
4. Метод введения новой переменной
Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах.
Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы.
Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы.
Рассмотрим эти случаи на примерах.
Первый вариант:
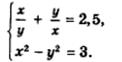
Введем новую переменную t = 
, тогда 
.
Решим первое уравнение относительно переменной t.
 |
- Все слагаемые перенесли в левую часть, приводим к общему знаменателю
ОДЗ: t 
0
- Оба корня удовлетворяют ОДЗ
Обратная замена: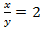 
=> х = 2у или 
=> у = 2х
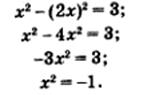Подставляем полученные выражения поочередно во второе уравнение.
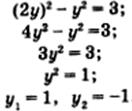
Тогда х1 = 2 х2 = -2
Ответ: (2; 1), (-2; -1)
Второй вариант:
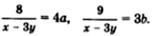
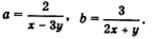
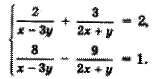
Вводим две новые переменные: Тогда
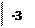Решим систему с новыми неизвестными:
- решаем методом алгебраического сложения
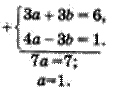Тогда b = 2 – 1 = 1.
Обратная замена:
=> =>
 |
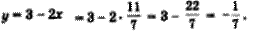
Тогда
Ответ: 
Системы неравенств
Несколько неравенств с одной переменной х образуют систему неравенств, если ставится задача найти все такие значения переменной, при которых каждое из заданных неравенств с переменной обращается в верное числовое неравенство.
Любое такое х называют решением системы неравенств.
Алгоритм решения систем неравенств:
1) Решить каждое неравенство, входящее в систему по отдельности.
Решением каждого неравенства является какое-то числовое множество.
2) Найти общее решение, т.е. найти пересечение найденных числовых множеств.
Пример:
- решим каждое из линейных неравенств отдельно
2х > 4 3x < 9
x > 2 x < 3
Изобразим эти числовые множества на координатных прямых друг под другом:
 |
Ответ: (2; 3)
poisk-ru.ru
2.1.8 Простейшие системы уравнений с двумя неизвестными
Видеоурок 1: Системы двух уравнений с двумя неизвестнымиВидеоурок 2: Решение систем уравнений
Лекция: Простейшие системы уравнений с двумя неизвестными
Уравнения с двумя неизвестнымиВ этой теме мы рассмотрим с Вами уравнения, которые содержат две неизвестных. Зачастую, чтобы решить подобного рода уравнения, нам необходимо иметь столько уравнений, сколько содержится неизвестных.
Уравнения с двумя неизвестными имеют следующий вид:
a, b, c, d - это числа, стоящие рядом в переменными (х, у).
Решить систему уравнения - это означает найти такое значение переменных, которые приведут оба уравнения в верное равенство.
Каждое из уравнений может иметь несколько ответов, однако ответом на систему уравнений будет та пара чисел, которая будет подходить обоим уравнениям.
Трактовать решение системы уравнений можно аналитическим способом, некоторые из которых мы рассмотрим позднее, и графическим способом.
Графический способ решения системы уравненийДля каждого из заданных уравнений можно построить свой график на плоскости - это может быть любой из известных графиков функции. Решением системы уравнений будет считаться точка, в которой будут пересекаться графики. Данная точка будет иметь свою координату, которой будет соответствовать ордината и абсцисса, которые будут являться решением.
На графике можно получить несколько видов решений:
1. Множество решений. Например, если одно уравнение будет представлять тригонометрическую функцию, а вторая - это прямая, например, параллельная оси ОХ, то данная прямая будет пересекать график второй функции во множестве точек с некой периодичностью.
2. Одно решение. В таком случае графики функций будут пересекаться в одной точке. Обычно такая картина наблюдается, если графиками уравнений являются прямые.
3. Два решения. То есть графики уравнений будут пересекаться в двух точках. Обычно такое наблюдается в том случае, если графиком одной из функций является парабола.
4. Не иметь решений. Некоторые графики функций и вовсе могут не пересекаться, в таком случае решений система иметь не будет.
Основные способы аналитического решенияРешать с помощью графика не всегда удобно, поскольку точка пересечения функций может находиться достаточно далеко от начала координат, или же она будет иметь дробные координаты. Чтобы наиболее точно найти решение системы, лучше воспользоваться аналитическими способами решения.
1. Подстановка
Чтобы решить систему методом подстановки, необходимо в одном из уравнений выразить одну из неизвестных и подставить её во второе уравнение.
x = ( c – by ) / a
d ( c – by ) / a + ey = f
После данной подстановки одно из уравнений будет иметь одну неизвестную, после чего уравнение решается известным способом. Когда одна из переменных найдена, её значение подставляется в первое уравнение и, таким образом, находится и вторая переменная.
2. Метод сложения или вычитание уравнений
Данный метод позволяет избавиться от одной из неизвестных. Итак, давайте представим, что вы желаете избавиться от переменной "х". Чтобы данный способ имел место, Вам необходимо первое уравнение почленно домножить на d, а второе почленно домножить на a. После этого Вы получите одинаковые коэффициенты при переменной "х". Если вычтите одно уравнение из другого, у Вас получится избавиться от одной неизвестной. Дальше уравнение известными способами.
cknow.ru
Системы линейных уравнений с двумя неизвестными
Системой \( m \) линейных алгебраических уравнений с двумя неизвестными называется система уравнений вида
\( \begin{cases} a_{11}\cdot x_1+a_{12}\cdot x_2=b_1,\\ a_{21}\cdot x_1+a_{22}\cdot x_2=b_2,\\ \cdots\cdots \cdots\cdots \cdots\cdots \cdots\\ a_{m1}\cdot x_1+a_{m2}\cdot x_2=b_m. \end{cases} \)(3.26)
Числа \( a_{ij},~i=1,\ldots,m,~j=1,2 \) называются коэффициентами системы; \( b_1,b_2,\ldots,b_m \) — свободными членами, \( x_1,x_2 \) — неизвестными.
Решением системы называется упорядоченная пара чисел \( (\alpha_1,\alpha_2) \) такая, что после замены неизвестных \( x_1,x_2 \) соответственно числами \( \alpha_1,\alpha_2 \) каждое уравнение системы превращается в верное числовое равенство. Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.
Система (3.26) называется однородной, если все свободные члены равны нулю:
\( \begin{cases} a_{11}\cdot x_1+a_{12}\cdot x_2=0,\\ a_{21}\cdot x_1+a_{22}\cdot x_2=0,\\ \cdots\cdots\cdots \cdots\cdots \cdots\cdots\\ a_{m1}\cdot x_1+a_{m2}\cdot x_2=0. \end{cases} \)(3.27)
В отличие от однородной, систему общего вида (3.26) называют неоднородной.
Систему (3.26) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
\( A=\begin{pmatrix}a_{11}&a_{12}\\\vdots&\vdots\\a_{m1}&a_{m2}\end{pmatrix}\!. \)
свободные члены записываем в столбец свободных членов \( b=\begin{pmatrix}b_1\\\vdots\\b_m\end{pmatrix} \) , а неизвестные — в столбец неизвестных \( x=\begin{pmatrix}x_1\\x_2\end{pmatrix} \)
Матричная запись неоднородной системы уравнений (3.26) имеет вид
а однородной:где символ \( o \) в правой части обозначает нулевой столбец размеров \( m\times1\colon\, o=\begin{pmatrix} 0\\\vdots\\0 \end{pmatrix} \) .
Блочная матрица \( (A\mid b)=\begin{pmatrix} a_{11}&a_{12}& \!\!\vline\!\!&b_1\\\vdots&\vdots&\!\!\vline\!\!&\vdots\\a_{m1}&a_{m2}&\!\!\vline\!\!&b_m\end{pmatrix} \) называется расширенной матрицей системы (3.26).
Рассматривается случай, когда все уравнения системы первой степени, т.е. коэффициенты при неизвестных каждого уравнения не равны нулю одновременно. Поэтому матрица \( A \) системы ненулевая, более того, все ее строки ненулевые.
В соответствии с матричной записью решением системы (3.28) называется столбец \( x=\begin{pmatrix}\alpha_1\\\alpha_2\end{pmatrix} \) , при подстановке которого в (3.28) получаем верное равенство для столбцов в левой и правой частях. В частности, нулевой столбец \( o \) является решением однородной системы (3.29), т.е. любая однородная система уравнений совместна.
Рангом системы уравнений (3.26) называется ранг матрицы \( A \) системы: \( r=\operatorname{rang}A \) , т.е. максимальное число линейно независимых строк матрицы \( A \) (максимальное число линейно независимых уравнений системы). Поскольку матрица системы (3.26) ненулевая и содержит два столбца, то ее ранг \( r=\operatorname{rang}A\leqslant2 \) . Ранг может быть равен либо единице ( \( r=1 \) , если все строки матрицы \( A \) пропорциональны), либо двум ( \( r=2 \) , если имеются две линейно независимые строки).
Выясним геометрический смысл и свойства решений системы уравнений (3.26).
Пусть на плоскости задана аффинная система координат \( Ox_1x_2 \) . Как показано ранее, множество точек \( X(x_1,x_2) \) , координаты которых удовлетворяют линейному уравнению с двумя неизвестными \( a_{i1}x_1+a_{i2}x_2=b_i \) , или \( a_{i1}x_1+a_{i2}x_2-b_i=0 \) , представляет собой прямую. Поэтому множество решений системы уравнений является пересечением прямых \( a_{i1}x_1+a_{i2}x_2-b_i=0,~i=1,\ldots,m \) .
Примеры пересечения прямых
Если ранг системы (3.26) равен 1, то коэффициенты при неизвестных всех уравнений пропорциональны. В этом случае любые две прямые параллельны (система уравнений несовместна (рис.3.31,а)) или совпадают (в этом случае вся система (3.26) равносильна одному, например, первому ее уравнению (рис.3.31,6)).
Если ранг системы равен 2, то в системе имеются хотя бы два линейно независимых уравнения. Прямые, соответствующие этим уравнениям, пересекаются, например, в точке \( X_0(x_{10},x_{20}) \) . Поэтому множество решений системы (3.26) либо одна точка (система совместна, все прямые проходят через точку \( X_0 \) , т.е. все прямые принадлежат собственному пучку прямых (рис.3.31,в)), либо пусто (система несовместна (рис.3.31,г)).
Для решения системы (3.26) обычно применяется метод Гаусса исключения неизвестных, при котором уравнения системы заменяются линейными комбинациями уравнений, содержащими меньшее количество неизвестных, при этом расширенная матрица системы приводится к ступенчатому виду. Продемонстрируем этот метод на примере.
Пример 3.17. Решить системы уравнений:
\( \mathsf{1)}\begin{cases}x_1-2x_2=1,\\2x_1-4x_2=2,\\x_1-2x_2=-1;\end{cases} \mathsf{2)}\begin{cases}x_1-2x_2=1,\\2x_1-4x_2=2,\\-x_1+2x_2=-1;\end{cases} \mathsf{3)}\begin{cases}x_1+2x_2=3,\\x_1-4x_2=-3,\\x_1-2x_2=-1;\end{cases} \mathsf{4)}\begin{cases}x_1+2x_2=3,\\x_1-4x_2=-2,\\x_1-2x_2=-1;\end{cases} \)
Изобразить множество решений на координатной плоскости \( Ox_1x_2 \) .
Решение.
1) Составляем расширенную матрицу системы \( (A\mid b)=\begin{pmatrix}1&-2&\!\!\vline\!\!&1\\2&-4&\!\!\vline\!\!&2\\1&-2&\!\!\vline\!\!&-1\end{pmatrix}. \)
Поскольку \( a_{11}=1\ne0 \) (элемент \( a_{11} \) — ведущий), прибавим ко второй и к третьей строкам первую, умноженную на \( (-2) \) и на \( (-1) \) соответственно:
\( (A\mid b)= \begin{pmatrix}1&-1&\!\!\vline\!\!&1\\2&-4&\!\!\vline\!\!&2\\1&-2&\!\!\vline\!\!&-1\end{pmatrix}\sim \begin{pmatrix}1&-2&\!\!\vline\!\!&1\\0&0&\!\!\vline\!\!&0\\0&0&\!\!\vline\!\!&-2\end{pmatrix}. \)
Последняя строка соответствует уравнению \( 0\cdot x_1+0\cdot x_2=-2 \) , которое не имеет решений. Следовательно, множество решений системы пустое (прямые, задаваемые уравнениями системы, изображены на рис.3.31,а).
2) Составляем расширенную матрицу системы \( (A\mid b)=\begin{pmatrix}1&-2&\!\!\vline\!\!&1\\2&-4&\!\!\vline\!\!&2\\-1&2&\!\!\vline\!\!&-1\end{pmatrix}. \)
Поскольку \( a_{11}=1\ne0 \) (элемент \( a_{11} \) — ведущий), прибавим к третьей строке первую, а ко второй — первую, умноженную на \( (-2): \)
\( (A\mid b)=\!\begin{pmatrix}1&-2&\!\!\vline\!\!&1\\2&-4&\!\!\vline\!\!&2\\-1&2&\!\!\vline\!\!&-1\end{pmatrix}\sim \begin{pmatrix}1&-2&\!\!\vline\!\!&1\\0&0&\!\!\vline\!\!&0\\0&0&\!\!\vline\!\!&0\end{pmatrix} ~\Leftrightarrow~ \begin{pmatrix}1&-2\\0&0\\0&0\end{pmatrix}{\cdot} \begin{pmatrix}x_1\\x_2\end{pmatrix}= \begin{pmatrix}1\\0\\0\end{pmatrix}. \)
Система равносильна одному уравнению \( x_1-2x_2=1 \) . Множество ее решений представляет собой прямую на координатной плоскости \( Ox_1x_2 \) . Координаты любой точки этой прямой удовлетворяют системе уравнений, следовательно, система имеет бесконечно много решений (рис.3.31,6).
3) Составляем расширенную матрицу системы \( (A\mid b)=\begin{pmatrix}1&2&\!\!\vline\!\!&3\\1&-4&\!\!\vline\!\!&-3\\1&-2&\!\!\vline\!\!&-1\end{pmatrix}. \)
Поскольку \( a_{11}=1\ne0 \) (элемент \( a_{11} \) — ведущий), прибавим ко второй и к третьей строкам первую строку, умноженную на (-1):
\( (A\mid b)= \begin{pmatrix} 1&2&\!\!\vline\!\!& 3\\ 1&-4& \!\!\vline\!\!&-3\\ 1&-2&\!\!\vline\!\!&-1\end{pmatrix}\sim \begin{pmatrix} 1&2&\!\!\vline\!\!&3\\0&-6&\!\!\vline\!\!&-6\\0&-4&\!\!\vline\!\!&-4\end{pmatrix}. \)
Разделим вторую строку на (-6), а затем к первой и третьей строкам прибавим вторую, умноженную на (-2) и на 4 соответственно:
\( (A\mid b)\,\sim \begin{pmatrix}1&2&\!\!\vline\!\!&3\\0&-6&\!\!\vline\!\!&-6\\0&-4&\!\!\vline\!\!&-4\end{pmatrix}\sim \begin{pmatrix} 1&2&\!\!\vline\!\!&3\\ 0&1&\!\!\vline\!\!&1\\0&-4&\!\!\vline\!\!&-4\end{pmatrix}\sim \begin{pmatrix} 1&0&\!\!\vline\!\!&1\\0&1&\!\!\vline\!\!&1\\0&0&\!\!\vline\!\!&0\end{pmatrix} ~\Leftrightarrow~ \begin{pmatrix}1&0\\0&1\\0&0\end{pmatrix}{\cdot} \begin{pmatrix}x_1\\x_2\end{pmatrix}= \begin{pmatrix} 1\\1\\0\end{pmatrix}. \)
Получили единственное решение \( x_1=1,~x_2=1 \) , которому соответствует точка \( X_0(1;1) \) на координатной плоскости (рис.3.31,в).
4) Составляем расширенную матрицу системы \( (A\mid b)=\begin{pmatrix}1&2&\!\!\vline\!\!&3\\1&-4&\!\!\vline\!\!&-2\\1&-2&\!\!\vline\!\!&-1\end{pmatrix}. \)
Поскольку \( a_{11}=1\ne0 \) (элемент \( a_{11} \) — ведущий), прибавим ко второй и к третьей строкам первую строку, умноженную на (-1):
\( (A\mid b)= \begin{pmatrix} 1&2&\!\!\vline\!\!&3\\ 1&-4&\!\!\vline\!\!&-2\\1&-2&\!\!\vline\!\!&-1\end{pmatrix}\sim \begin{pmatrix}1&2&\!\!\vline\!\!&3\\0&-6&\!\!\vline\!\!&-5\\0&-4&\!\!\vline\!\!&-4\end{pmatrix}. \)
Разделим третью строку на (-4), а затем ко второй строке прибавим третью, умноженную на 6:
\( (A\mid b)\,\sim \begin{pmatrix} 1&2&\!\!\vline\!\!&3\\ 0&-6&\!\!\vline\!\!&-5\\0&-4&\!\!\vline\!\!&-4\end{pmatrix}\sim \begin{pmatrix} 1&2&\!\!\vline\!\!&3\\ 0&-6&\!\!\vline\!\!&-5\\ 0&1& \!\!\vline\!\!&1 \end{pmatrix}\sim \begin{pmatrix} 1&2&\!\!\vline\!\!&3\\ 0&0&\!\!\vline\!\!&1\\0&1&\!\!\vline\!\!&1\end{pmatrix}. \)
Вторая строка соответствует уравнению \( 0\cdot x_1+0\cdot x_2=1 \) , которое не имеет решений. Следовательно, система несовместна (прямые, задаваемые уравнениями системы, изображены на рис.3.31,2).
В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Источник
calcsbox.com
определение, алгоритм и методы решения, примеры
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
- 10x + 25y = 180.
- x — y = 6.
- -6x + y = 7.
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
- 20y — 3x = 16;
- -3x = 16−20y.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Пример:
- y — x = 6*2;
- 2y — 2x = 12.
Оба уравнения также равносильны.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
Последовательность действий:
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
Этапы решения:
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
liveposts.ru
Содержание
Инструкция
|
completerepair.ru
Как решать систему уравнений с двумя неизвестными | ЧтоКак.ру
Уравнение – это тождество, где среди известных членов скрывается одно число, которое необходимо поставить вместо латинской буквы, для того чтобы с левой и правой стороны получилось одинаковое числовое выражение. Чтобы его найти, нужно перенести в одну сторону все известные члены, в другую — все неизвестные члены уравнения. А как решать систему из двух таких уравнений? По отдельности – нельзя, следует связать искомые величины из системы друг с другом. Сделать это можно тремя способами: методом подстановки, методом сложения и методом построения графиков.
Инструкция
1
Способ сложения.Нужно записать два уравнения строго друг под другом: 2 –5у=61-9х+5у=-40.Далее, сложить каждое слагаемое уравнений соответственно, учитывая их знаки:2х+(-9х)=-7х, -5у+5у=0, 61+(-40)=21. Как правило, одна из сумм, содержащая неизвестную величину, будет равна нулю. Составить уравнение из полученных членов:-7х+0=21.Найти неизвестное: -7х=21, ч=21:(-7)=-3.Подставить уже найденное значение в любое из исходных уравнений и получить второе неизвестное, решив линейное уравнение:2х–5у=61, 2(-3)–5у=61, -6-5у=61, -5у=61+6, -5у=67, у=-13,4.Ответ системы уравнений: х=-3, у=-13,4.
2
Способ подстановки.Из одного уравнения следует выразить любое из искомых членов:х–5у=61-9х+4у=-7.х=61+5у, х=61+5у.Подставить получившееся уравнение во второе вместо числа «икс» (в данном случае):-9(61+5у)+4у=-7.Далее решивлинейное уравнение, найти число «игрек»:-549+45у+4у=-7, 45у+4у=549-7, 49у=542, у=542:49, у?11.В произвольно выбранное (из системы) уравнение вставить вместо уже найденного «игрека» число 11 и вычислить второе неизвестное:Х=61+5*11, х=61+55, х=116.Ответ данной системы уравнений: х=116, у=11.
3
Графический способ.Заключается в практическом нахождении координаты точки, в которой пересекаются прямые, математически записанные в системе уравнений. Следует начертить графики обоих прямых по отдельности в одной системе координат. Общий вид уравнения прямой: – у=kх+b. Чтобы построить прямую, достаточно найти координаты двух точек, причем, х выбирается произвольно.Пусть дана система: 2х – у=4 у=-3х+1.Строится прямая по первому уравнению, для удобства его нужно записать: у=2х-4. Придумать (полегче) значения для икс, подставляя его в уравнение, решив его, найти игрек. Получаются две точки, по которым строится прямая. (см рис.)х 0 1у -4 -2Строится прямая по второму уравнению: у=-3х+1.Так же построить прямую. (см рис.)х 0 2у 1 -5Найти координаты точки пересечения двух построенных прямых на графике (если прямые не пересекаются, то система уравнений не имеет решения – так бывает).
chtokak.ru
