54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции. Точка минимума и максимума
Как найти экстремум (точки минимума и максимума) функции
- Находим производную функции
- Приравниваем эту производную к нулю
- Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
- Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
- Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.
Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.
Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.
https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru
Рассмотрим пример Находим производную и приравниваем её к нулю:Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.
Смотрите также:
Еще больше материалов для подготовки к ЕГЭ
bugaga.net.ru
Как найти точки минимума и максимума функции: особенности, способы и примеры
Функция и исследование ее особенностей занимает одно из ключевых глав в современной математике. Главная составляющая любой функции - это графики, изображающие не только ее свойства, но также и параметры производной данной функции. Давайте разберемся в этой непростой теме. Итак, как лучше искать точки максимума и минимума функции?
Функция: определение
Любая переменная, которая каким-то образом зависит от значений другой величины, может называться функцией. Например, функция f(x2) является квадратичной и определяет значения для всего множества х. Допустим, что х = 9, тогда значение нашей функции будет равно 92= 81.
Функции бывают самых разных видов: логические, векторные, логарифмические, тригонометрические, числовые и другие. Их изучением занимались такие выдающиеся умы, как Лакруа, Лагранж, Лейбниц и Бернулли. Их труды служат оплотом в современных способах изучения функций. Перед тем как найти точки минимума, очень важно понять сам смысл функции и ее производной.
Производная и ее роль
Все функции находятся в зависимости от их переменных величин, а это значит, что они могут в любой момент изменить свое значение. На графике это будет изображаться как кривая, которая то опускается, то поднимается по оси ординат (это все множество чисел "y" по вертикали графика). Так вот определение точки максимума и минимума функции как раз связано с этими "колебаниями". Объясним, в чем эта взаимосвязь.
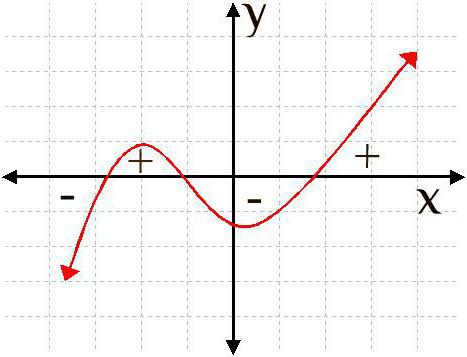
Производная любой функции изображается на графике с целью изучить ее основные характеристики и вычислить, как быстро изменяется функция (т.е. меняет свое значение в зависимости от переменной "x"). В тот момент, когда функция увеличивается, график ее производной будет также возрастать, но в любую секунду функция может начать уменьшаться, и тогда график производной будет убывать. Те точки, в которых производная переходит со знака минуса на плюс, называются точками минимума. Для того чтобы знать, как найти точки минимума, следует лучше разобраться с понятием производной.
Как вычислять производную?

Математический способ ее определения для многих учеников кажется сложным, однако на самом деле все гораздо проще. Необходимо лишь следовать стандартному плану нахождения производной любой функции. Ниже описано, как можно найти точку минимума функции, не применяя правила дифференцирования и не заучивая таблицу производных.
- Вычислить производную функции можно с помощью графика. Для этого необходимо изобразить саму функцию, затем взять на ней одну точку (точка А на рис.) Вертикально вниз провести линию к оси абсцисс (точка х0), а в точке А провести касательную к графику функции. Ось абсцисс и касательная образуют некий угол а. Для вычисления значения того, насколько быстро возрастает функция, необходимо вычислить тангенс этого угла а.
- Получается, что тангенс угла между касательной и направлением оси х является производной функции на маленьком участке с точкой А. Данный метод считается геометрическим способом определения производной.
Способы исследования функции
В школьной программе математики возможно нахождение точки минимума функции двумя способами. Первый метод с помощью графика мы уже разобрали, а как же определить численное значение производной? Для этого потребуется выучить несколько формул, которые описывают свойства производной и помогают преобразовать переменные величины типа "х" в числа. Следующий метод является универсальным, поэтому его можно применять практически ко всем видам функций (как к геометрическим, так и логарифмическим).
- Необходимо приравнять функцию к функции производной, а затем упростить выражение, используя правила дифференцирования.
- В некоторых случаях, когда дана функция, в которой переменная "х" стоит в делителе, необходимо определить область допустимых значений, исключив из нее точку "0" (по простой причине того, что в математике ни в коем случае нельзя делить на ноль).
- После этого следует преобразовать изначальный вид функции в простое уравнение, приравняв все выражение к нулю. Например, если функция выглядела так: f(x) = 2x3+38x, то по правилам дифференцирования ее производная равна f'(x) = 3x2+1. Тогда преобразуем это выражение в уравнение следующего вида: 3x2+1 = 0.
- После решения уравнения и нахождения точек "х", следует изобразить их на оси абсцисс и определить, является ли производная в этих участках между отмеченными точками положительной или отрицательной. После обозначения станет ясно, в какой точке функция начинает убывать, то есть меняет знак с минуса на противоположный. Именно таким способом можно найти как точки минимума, так и максимума.
Правила дифференцирования
Самая основная составляющая в изучении функции и ее производной - это знание правил дифференцирования. Только с их помощью можно преобразовывать громоздкие выражения и большие сложные функции. Давайте ознакомимся с ними, их достаточно много, но все они весьма просты благодаря закономерным свойствам как степенных, так и логарифмических функций.
- Производная любой константы равна нулю (f(х) = 0). То есть производная f(х) = x5+ х - 160 примет такой вид: f' (х) = 5x4+1.
- Производная суммы двух слагаемых: (f+w)' = f'w + fw'.
- Производная логарифмической функции: (logad)' = d/ln a*d. Эта формула применима ко всем видам логарифмов.
- Производная степени: (xn)'= n*xn-1. Например,(9x2)' = 9*2x = 18x.
- Производная синусоидальной функции: (sin a)' = cos a. Если sin угла а равен 0,5, то ее производная равна √3/2.
Точки экстремума
Мы уже разобрали, как найти точки минимума, однако существует понятие и точек максимума функции. Если минимум обозначает те точки, в которых функция переходит со знака минуса на плюс, то точками максимума являются те точки на оси абсцисс, на которых производная функции меняется с плюса на противоположный - минус.
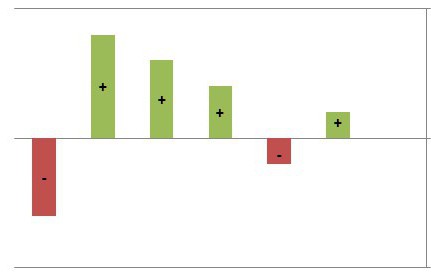
Находить точки максимума можно по вышеописанному способу, только следует учесть, что они обозначают те участки, на которых функция начинает убывать, то есть производная будет меньше нуля.
В математике принято обобщать оба понятия, заменяя их словосочетанием "точки экстремумов". Когда в задании просят определить эти точки, это значит, что необходимо вычислить производную данной функции и найти точки минимума и максимума.
fb.ru
как найти критическую точку максимума и минимума

Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
...
Вконтакте
Google+
Мой мир
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
- экономика;
- статистика;
- биология;
- машинное управление;
- эконометрика.
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.

Производная функция
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Острый экстремум
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.

Острый экстремум
Важно! Процесс нахождения точек острого экстремума функции называется дифференцированием и используется как в школьном курсе изучения алгебры и начала анализа, так и в ходе освоения высшей математики в университете.
Экстремальное значение функции
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.
- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.
- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.

Экстремальное значение функции
Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.

Точки минимума и максимума
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум.
| Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума.
|
Экстремум функционала
Для того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил:
- определить необходимое условие экстремального отношения;
- учитывать достаточное условие крайних точек на графике;
- осуществлять расчет острого экстремума.
Используются также такие понятия, как слабый минимум и сильный минимум. Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Экстремумы функции. 10 класс.
Исследование функции. Экстремумы функции — bezbotvy
Вывод
После прочтения и осознания данной статьи любой новичок в математике имеет возможность понять возможности острых экстремумов в том виде, в каком они используются в образовательном процессе. Вышеперечисленные моменты позволяют разобраться в крайних точках без помощи репетиторов.
uchim.guru
матан коллоквиум / 12.Понятие экстренума.Определение максиимума,минимума,понятие критической точки,графическая иллюстрация критических точек
Экстре́мум (лат. extremum — крайний) в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть дана функция и— внутренняя точка области определенияТогда
Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.
Значение функции называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
Достаточные условия существования локальных экстремумов
является точкой строгого локального максимума. А если
то является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке
и
является точкой локального максимума. А если
и
то является точкой локального минимума.
Если чётно и, то- точка локального максимума. Есличётно и, то- точка локального минимума. Еслинечётно, то экстремума нет.
Максимум и минимум функции.
Приведем точные определения точек экстремума. Определение. Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0. Это наглядно показано на рисунке 1: рисунок 1 Определение. Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0. Это наглядно показано на рисунке 2: рисунок 2 По определению значение функции f в точке x0 является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x0 имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно). В окрестности точки минимума графики изображаются в виде загругленной или острой впадины (рис. 2 а) и б) соответственно). Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже: Слева направо: a - точка максимума; a - точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума. Для точек минимума и максимума функции есть общее определение - точки экстремума. Значение функции в этих точках соответственно назывется максимумом или минимумом этой функции. Общее название - экстремум функции. Точки максимума обычно обозначают xmax, а точки минимума - xmin.
Критической точкой дифференцируемой функции , где — область в , называется точка, в которой все её частные производные обращаются в ноль. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.
studfiles.net
54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.
Экстремумом функцииназывается максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называетсяточкой экстремума. Точканазывается точкойлокального максимума функции, если выполняется условие:Аналогично точканазывается точкойлокального минимума функции, если выполняется условие:
Точки, в которых производнаяравна нулю, называютсястационарными точками. Точки, в которых функциянепрерывна, а её производная либо равна нулю, либо не существует, называютсякритическимиточками.
Теорема (необходимое условие экстремума)
Если точка — точка экстремума функции, то она критическая.
Доказательство
По условию точка — точка экстремума функциипо теореме Фермапроизводнаяточкаявляется критической.
Пример:
Найти экстремум функции . Найдем производную этой функции:критические точки задаются уравнением. Корни этого уравненияи.
Как видно по рисунку функция имеет максимум в точке 1, а минимум в точке 3. Подставим эти значения чтобы убедиться в исходную функцию: ив точкефункция имеет минимум, равный -4, а в точкефункция имеет максимум, равный 0.
Замечания:
Не всякая критическая точка является точкой экстремума.
Пример:
Рассмотрим функцию . Построим график этой функции:
Производная данной функции в точке по определению является критической точкой, однако в этой точке функция не имеет экстремума.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция определена идифференцируемав некоторой окрестности точки, кроме, быть может, самой точкии непрерывна в этой точке. Тогда:
Если производная меняет знак с «-» на «+» при переходе через точку:и, то— точка строго минимума функции
Если производная меняет знак с «+» на «-» при переходе через точку:и, то— точка строго максимума функции
Доказательство
Пусть, например, меняет знак с «-» на «+». Рассмотрим точкуна сегментеВоспользуемся теоремой о конечных приращениях Лагранжа:,. Поскольку при переходе через точкуфункция меняет знак с «-» на «+», тои, тоАналогично рассмотрим сегмент, получим— точка строгого минимума функции.
Замечания:
Если — точка строго экстремума, то из этого не следует, что производнаяменяет знак при переходе через точку
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть дана функция , она определена в некоторой окрестности точки, ее перваяпроизводнаяи пусть, тогда:
Если , то точка— точка строгого минимума;
Если , то точка— точка строгого максимума.
Доказательство
Докажем теорему для первого случая, когда . По сколькунепрерывна, то на достаточно малом интервале, т.к, товозрастает в этом интервале., значитна интервалеина интервале. Таким образом функцияубывает на интервалеи возрастает на интервалепо первому достаточному условию экстремума функция в точкеимеет минимум. Аналогично доказывается второй случай теоремы.
Замечания:
Если и, то функцияможет и не иметь экстремум в точке
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)
Пусть функция определена в некоторой окрестности точки, и в этой точке существуют производные до n-го порядка пусть,и,Тогда:
Если (т.е— четное), то— точка экстремума:
если , то— точка локального максимума;
если , то— точка локального минимума;
Если (т.е— нечетное), то— не является точкой экстремума.
Доказательство
Воспользуемся формулой Тейлора в окрестности точки с остатком в форме Пеано:. По скольку все производные допорядка включительно равны нулю получим:Запишем полученное выражение в виде:. Выражение. Пусть,. Отсюда следует, что сохранение или изменение знака приращения функции во время перехода через точкузависит от четности. Последний факт и доказывает теорему.
Определение. Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0. Это наглядно показано на рисунке 1:рисунок 1 Определение.Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0. Это наглядно показано на рисунке 2:рисунок 2 По определению значение функции f в точке x0является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x0имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно). В окрестности точки минимума графики изображаются в виде загругленной или острой впадины (рис. 2 а) и б) соответственно). Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже:Слева направо: a - точка максимума; a - точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума. Для точек минимума и максимума функции есть общее определение -точки экстремума. Значение функции в этих точках соответственно назыветсямаксимумом или минимумом этой функции. Общее название -экстремум функции. Точки максимума обычно обозначают xmax, а точки минимума - xmin.
studfiles.net
Как найти точки минимума и максимума функции
Задание.Найти точки минимума и максимума функции 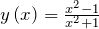 .
.
Решение.При исследовании функции на минимум или максимум всегда находят производную.Итак, найдем первую производную функции, используя правило производной от дроби:
![Rendered by QuickLaTeX.com \[y'\left(x\right)={\left(\frac{x^2-1}{x^2+1}\right)}'=\frac{{\left(x^2-1\right)}'\cdot \left(x^2+1\right)-\left(x^2+1\right)'\cdot \left(x^2-1\right)}{{\left(x^2+1\right)}^2}=\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ad37d4e05ccc3396d4ca32d7ac71d78f_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{2x\cdot \left(x^2+1\right)-2x\cdot \left(x^2-1\right)}{{\left(x^2+1\right)}^2}=\frac{2x\cdot \left(x^2+1-x^2+1\right)}{{\left(x^2+1\right)}^2}=\frac{4x}{{\left(x^2+1\right)}^2}\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9942c94aff25d29254518349aaad3029_l3.png)
Далее определим точки, в которых производная обращается в ноль. Для этого приравняем выражение производной к нулю и решим уравнение:
![Rendered by QuickLaTeX.com \[y'\left(x\right)=0\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1d710c204897339cc7b8a12249705e92_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4x}{{\left(x^2+1\right)}^2}=0\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d6dd7a305311e0bfd9ba97be8eeb99eb_l3.png)
![Rendered by QuickLaTeX.com \[4x=0\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d2477a5c9b534e706a8f5f3240bf81a7_l3.png)
![Rendered by QuickLaTeX.com \[x=0\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c4849919a4f0f9dce671d5f9da30fb1f_l3.png)
Итак, производная обращается в нуль в точке 0.Далее найдем вторую производную от функции. Для этого найдем производную от первой производной, используя также производную от сложной функции:
![Rendered by QuickLaTeX.com \[y''\left(x\right)={\left(\frac{4x}{{\left(x^2+1\right)}^2}\right)}'=\frac{{\left(4x\right)}'\cdot {\left(x^2+1\right)}^2-\left({\left(x^2+1\right)}^2\right)'\cdot 4x}{{\left(x^2+1\right)}^4}=\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-16d735343e13bc3eb5862d7f7e328d5a_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{4\cdot {\left(x^2+1\right)}^2-2\cdot \left(x^2+1\right)\cdot 2x\cdot 4x}{{\left(x^2+1\right)}^4}=\frac{4\cdot {\left(x^2+1\right)}^2-16x^2\cdot \left(x^2+1\right)}{{\left(x^2+1\right)}^4}=\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c96766b0f0b8a0595d3342aa2d894ec9_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{\left(x^2+1\right)\cdot \left(4\cdot \left(x^2+1\right)-16x^2\right)}{{\left(x^2+1\right)}^4}=\frac{4x^2+4-16x^2}{{\left(x^2+1\right)}^3}=\frac{4-12x^2}{{\left(x^2+1\right)}^3}=\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4b26c367afb8838dd6c0637a2d946ef1_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{4\cdot \left(1-3x^2\right)}{{\left(x^2+1\right)}^3}\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-954227e099d9cb0a790204b5cd7364a7_l3.png)
Найдем знак производной в точке х = 0:
![Rendered by QuickLaTeX.com \[y''\left(0\right)=\frac{4\cdot \left(1-3\cdot 0^2\right)}{{\left(0^2+1\right)}^3}=\frac{4}{1}=4>0\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7bec2b64111ae37378e886ba416cd0f9_l3.png)
Делаем вывод, что в данной точке х = 0 функция имеет минимум.Найдем значение функции в этой точке, подставив значение 0 в ее уравнение:
![Rendered by QuickLaTeX.com \[y\left(0\right)=\frac{0^2-1}{0^2+1}=-1\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-33917c57d2b9a973a803c2c6d555c570_l3.png)
Ответ. (0; —1).
Данное задание можно решить и при помощи только первой производной. При таком решении нужно находить знаки производной на обоих полученных интервалах, на которые разбивает числовую прямую точка 0.
ru.solverbook.com
Экстремумы функции, максимум и минимум
ОПРЕДЕЛЕНИЕЭкстремумами (максимумами и минимумами) функции называются значения функции в точках максимума и минимума.
Точки экстремума функции
Говорят, что в точке 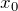 максимум (минимум), если существует такая
максимум (минимум), если существует такая 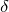 -окрестность точки
-окрестность точки 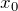 —
— 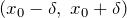 , что для всех
, что для всех 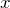 из этой окрестности, отличных от
из этой окрестности, отличных от 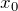 выполняется неравенство
выполняется неравенство 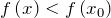
 .
.
Точки максимума и минимума называются точками экстремума.
ОПРЕДЕЛЕНИЕ Точки области определения, в которых производная функции равна нулю или не существует, называются критическими точками.Необходимое условие существования экстремума функции. Пусть функция 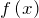 дифференцируема в промежутке
дифференцируема в промежутке 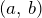 . Если в некоторой точке
. Если в некоторой точке 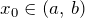 функция
функция 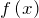 имеет экстремум, то в этой точке производная равна нулю:
имеет экстремум, то в этой точке производная равна нулю: 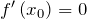 .
.
Достаточное условие существования экстремума функции. Если производная функции 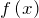 равна нулю в точке
равна нулю в точке 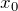 и при переходе через эту точку в сторону возрастания
и при переходе через эту точку в сторону возрастания 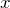 меняет знак с «+» («-») на «-» («+»), то в точке
меняет знак с «+» («-») на «-» («+»), то в точке 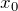 функция имеет максимум (минимум). Если же при переходе через точку
функция имеет максимум (минимум). Если же при переходе через точку 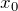 производная функции не меняет знак, то в этой точке функция
производная функции не меняет знак, то в этой точке функция 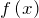 экстремума не имеет.
экстремума не имеет.
Для исследования функции на экстремум необходимо:
- найти критические точки функции;
- проверить, изменяет ли знак производная функции при переходе через критическую точку;
- вычислить значения максимума
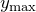 или минимума
или минимума  .
.
Примеры исследования функции на экстремум
ПРИМЕР 1| Задание | Найти экстремум функции 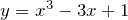 |
| Решение | Найдем критические точки функции, для этого вычислим производную заданной функции
приравняем её к нулю и найдем корни полученного квадратного уравнения Получили две критические точки 
В точке В точке |
| Ответ |
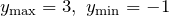 |
| Задание | Найти экстремум функции
|
| Решение | Область определения функции 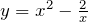 — вся числовая прямая, за исключением точки — вся числовая прямая, за исключением точки 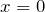 , то есть , то есть 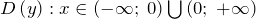 . .
Вычислим производную заданной функции и найдем критические точки Приравниваем к нулю производную Получаем одну критическую точку 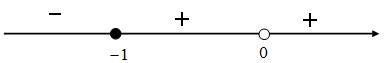
В точке |
| Ответ |
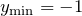 |
Монотонность функции
Нули функции
Наибольшее и наименьшее значение функции
Точки перегиба функции
Промежутки выпуклости и вогнутости функции
Исследование функции
ru.solverbook.com

![Rendered by QuickLaTeX.com \[y'=3x^{2} -3,\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b06dd3dfe6a266d40448834982ed28a6_l3.png)
![Rendered by QuickLaTeX.com \[3x^{2} -3=0\Rightarrow x^{2} -1=0\Rightarrow \left(x-1\right)\left(x+1\right)=0\Rightarrow x_{1} =-1,\quad x_{2} =1\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5d5df59cefab8bb7753ad6c9f535e122_l3.png)
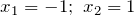 . Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах.
. Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах.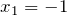 производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума
производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума ![Rendered by QuickLaTeX.com \[y_{\max } =y\, \left(-1\right)=\left(-1\right)^{3} -3\cdot \left(-1\right)+1=-1+3+1=3\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5968e93ccd8ff9284f3f8d035dba5934_l3.png)
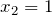 производная меняет знак с «-» на «+», значит,
производная меняет знак с «-» на «+», значит, 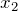 — точка минимума. Значение минимума соответственно равно
— точка минимума. Значение минимума соответственно равно ![Rendered by QuickLaTeX.com \[y_{\min } =y\, \left(1\right)=1^{3} -3\cdot 1+1=1-3+1=-1\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b8aac565d7f503c08efb2ad4fa8e8301_l3.png)
![Rendered by QuickLaTeX.com \[y=x^{2} -\frac{2}{x}\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d048d3539a57c2be85e0ea1ef8bafd5d_l3.png)
![Rendered by QuickLaTeX.com \[y'=2x+\frac{2}{x^{2} } \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-16991b498931d2b31d52db756427aff3_l3.png)
![Rendered by QuickLaTeX.com \[2x+\frac{2}{x^{2} } =0\Rightarrow \frac{2x^{3} +2}{x^{2} } =0\Rightarrow 2\left(x^{3} +1\right)=0\Rightarrow x^{3} =-1\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8112fe9445695e7962629c44669915f0_l3.png)
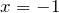 . Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах
. Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах![Rendered by QuickLaTeX.com \[y_{\min } =y\, \left(1\right)=1^{2} -\frac{2}{1} =-1\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9a6a4957eea96c457c6d98384a41f365_l3.png)