ГлавнаяРазноеУглы в пятиугольнике

Правильный пятиугольник. Углы в пятиугольнике


Правильный пятиугольник | Треугольники

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен

∠A1O A2=360º:5=72º.

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника,  боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

В треугольнике A1OA5

   

   

   

Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть

   

   

OF — радиус вписанной в A1A2A3A4A5 окружности: OF=r.

Рассмотрим прямоугольный треугольник A1OF.

По определению синуса,

   

откуда

   

   

Так как

   

то

   

   

   

   

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

   

По определению котангенса,

   

   

Подставив значение котангенса 36°, получаем:

   

Итак, формула радиуса вписанной в правильный пятиугольник окружности

   

Применив формулу

   

можно найти площадь правильного пятиугольника. Здесь

   

следовательно, формула для нахождения площади A1A2A3A4A5

   

Все диагонали правильного пятиугольника равны.

Длина диагонали равна

   

www.treugolniki.ru

Правильный пятиугольник | Формулы и расчеты онлайн

Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.

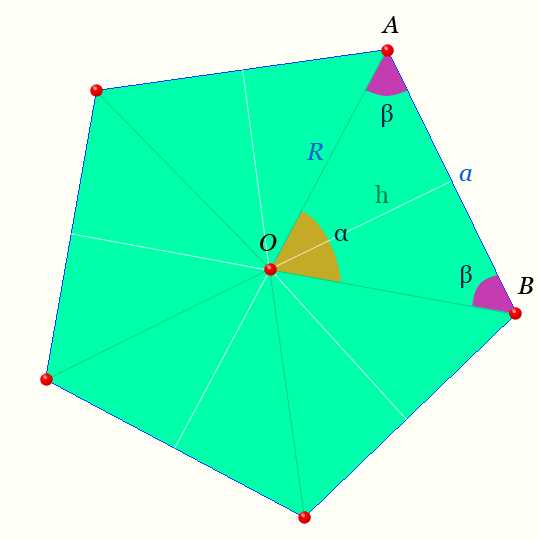
Правильный пятиугольник

Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного пятиугольника.

Обозначения на рисунке для правильного пятиугольника

n=5αβγaR
pLh
число сторон и вершин правильного пятиугольника,шт
центральный угол правильного пятиугольника,радианы, °
половина внутреннего угла правильного пятиугольника,радианы, °
внутренний угол правильного пятиугольника,радианы, °
сторона правильного пятиугольника,м
радиусы правильного пятиугольника,м
полупериметр правильного пятиугольника,м
периметр правильного пятиугольника,м
апофемы правильного пятиугольника,м

Основные формулы для правильного пятиугольника

Периметр правильного пятиугольника

\[ L = 5a \]

Полупериметр правильного пятиугольника

\[ p = \frac{5}{2}a \]

Центральный угол правильного пятиугольника в радианах

\[ α = \frac{2}{5}π \]

Центральный угол правильного пятиугольника в градусах

\[ α = \frac{360°}{5} = 72° \]

Половина внутреннего угла правильного пятиугольника в радианах

\[ β = \frac{3}{10}π \]

Половина внутреннего угла правильного пятиугольника в градусах

\[ β = \frac{3}{10}180° = 54° \]

Внутренний угол правильного пятиугольника в радианах

\[ γ = 2β = \frac{3}{5}π \]

Внутренний угол правильного пятиугольника в градусах

\[ γ = \frac{3}{5}180° = 108° \]

Площадь правильного пятиугольника

\[ S = ph = \frac{5}{2}ha \]

Или учитывая формулу Площади правильного пятиугольника получим

\[ S = \frac{5}{2} · a · \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]

Отсюда получим апофему правильного пятиугольника

\[ h = \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]

В помощь студенту

Правильный пятиугольник
стр. 268

www.fxyz.ru

Правильный пятиугольник: необходимый минимум информации

Толковый словарь Ожегова гласит, что пятиугольник представляет собой геометрическую фигуру, ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).

Чем интересен правильный пятиугольник?

Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!

Основные свойства и формулы

Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.

S = (n*a*r)/2 = 2,5*a*r либо S = (n*R2*sin α)/2 ≈ 2,3776*R2;

S = (5*a2*tg54°)/4 ≈ 1,7205* a2.

Правильный пятиугольник: построение

Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.

1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.

2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.

3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.

4. На середине расстояния между точками О и В постройте точку С.

5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.

6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.

7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить точкой G.

8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.

9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!

fb.ru

Правильный пятиугольник Википедия

Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

Построение правильного пятиугольника α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}S=54t2ctgπ5=55+254t2=512Rd=52R2sin⁡2π5=5r2tgπ5{\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}}, где R{\displaystyle R} — радиус описанной окружности, r{\displaystyle r} — радиус вписанной окружности, d{\displaystyle d} — диагональ, t{\displaystyle t} — сторона.h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1,539t}

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541} где Φ{\displaystyle \Phi } — отношение золотого сечения.

Построение

Построение правильного пятиугольника

Построение правильного пятиугольника

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Вот один из методов построения правильного пятиугольника в заданной окружности:

  1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
  2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
  3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
  4. Постройте точку C посередине между O и B.
  5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
  6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
  7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
  8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
  9. Постройте правильный пятиугольник AEGHF.
Пятиугольный узел на полоске бумаги

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.

Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

Интересные факты

См. также

Примечания

МногоугольникиЗвёздчатые многоугольникиПаркеты на плоскостиПравильные многогранникии сферические паркетыМногогранники Кеплера — ПуансоСотыЧетырёхмерные многогранники
  • {3,3,3}
  • {4,3,3}
  • {3,3,4}
  • {3,4,3}
  • {5,3,3}
  • {3,3,5}

wikiredia.ru

Правильный пятиугольник - это... Что такое Правильный пятиугольник?

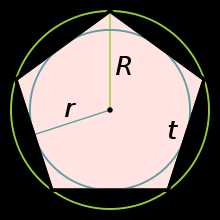Правильный пятиугольник

Правильный пятиугольник (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

Построение правильного пятиугольника , где  — радиус описанной окружности,  — радиус вписанной окружности, — диагональ, — сторона.

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

, где — отношение золотого сечения.

Построение

Построение правильного пятиугольника

Построение правильного пятиугольника

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

  1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
  2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
  3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью, как точку B.
  4. Постройте точку C посередине между O и B.
  5. Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
  6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
  7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
  8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
  9. Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Overhand knot of a paper strip

В природе

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1]

Интересные факты

Пентагон

См. также

Примечания

dic.academic.ru

Правильный пятиугольник — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

{2}};

|угол=108° |свойства= выпуклый, вписанный, Равносторонний, равноугольный[en], изотоксальный[en] }}

Правильный пятиугольник (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

<math>\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{3}{5} \cdot 180^\circ = 108^\circ</math> <math>S = \frac{5}{4} t^2 \mathop{\mathrm{ctg}}\, \frac{\pi}{5} = \frac{\sqrt 5 \sqrt{5 + 2 \sqrt{5}}}{4} t^2 = \frac{5}{12}Rd = \frac{5}{2} R^2 \sin \frac{2 \pi}{5} = 5 r^2 \mathop{\mathrm{tg}}\, \frac{\pi}{5}</math>, где <math>R</math> — радиус описанной окружности, <math>r</math> — радиус вписанной окружности, <math>d</math> — диагональ, <math>t</math> — сторона. <math>h= \frac{\operatorname{tg}\,72^\circ}{2} t = \frac{\sqrt{5 + 2 \sqrt{5}}}{2} t \approx 1,539 t</math>

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

<math>t =R \sqrt{\frac{5 - \sqrt{5}}{2}}</math> <math>r = \frac{\sqrt 5 \sqrt{5 + 2 \sqrt{5}}}{10} t</math> <math>R = \frac{\sqrt 10 \sqrt{5 + \sqrt{5}}}{10} t = ( \sqrt 5 - 1) r</math>

<math>d = R{\sqrt {\varphi{\sqrt5}}} </math>

<math>S = \frac{\sqrt 5 \sqrt{5 + 2 \sqrt{5}}}{4} t^2</math> <math>\frac{S}{s} = \varphi^4 = 3\varphi + 2 = \frac{3\sqrt{5} + 7}{2} \approx 6,8541</math> где <math>\varphi</math> — отношение золотого сечения.

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э. Вот один из методов построения правильного пятиугольника в заданной окружности:

  1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
  2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
  3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
  4. Постройте точку C посередине между O и B.
  5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
  6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
  7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
  8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
  9. Постройте правильный пятиугольник AEGHF.

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.

Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

Интересные факты

См. также

Напишите отзыв о статье "Правильный пятиугольник"

Примечания

  1. ↑ [www.nature.com/nmat/journal/vaop/ncurrent/full/nmat2403.html A one-dimensional ice structure built from pentagons. Nature Materials. 8 March 2009] (англ.)
МногоугольникиЗвёздчатые многоугольникиПаркеты на плоскостиПравильные многогранникии сферические паркетыМногогранники Кеплера — ПуансоСотыЧетырёхмерные многогранники
{3,3,3} · {4,3,3} · {3,3,4} · {3,4,3} · {5,3,3} · {3,3,5}

Отрывок, характеризующий Правильный пятиугольник

Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева. – Готово, ваше благородие, надвое хранцуза распластаете. Петя очнулся. – Уж светает, право, светает! – вскрикнул он. Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги. – Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.

Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало. – Ну, готово у вас все? – сказал Денисов. – Давай лошадей. Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову. – Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него. – Об одном тебя пг'ошу, – сказал он строго, – слушаться меня и никуда не соваться. Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него. – Сигнал! – проговорил он. Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы. В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади. У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики. – Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице. Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему. – Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову. Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете. – Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову. – Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети. – Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.

wiki-org.ru

Правильный пятиугольник — WiKi

Свойства

Построение правильного пятиугольника α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }} S=54t2ctgπ5=55+254t2=512Rd=52R2sin⁡2π5=5r2tgπ5{\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}} , где R{\displaystyle R}  — радиус описанной окружности, r{\displaystyle r}  — радиус вписанной окружности, d{\displaystyle d}  — диагональ, t{\displaystyle t}  — сторона.h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1,539t} 

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R} r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t} R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r} d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t} S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}} Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}  где Φ{\displaystyle \Phi }  — отношение золотого сечения.

Построение

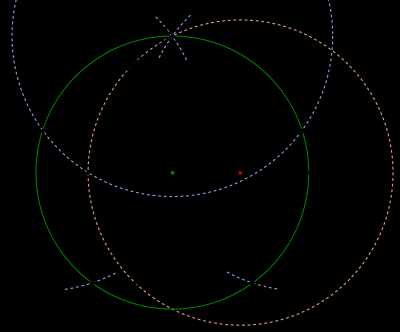  Построение правильного пятиугольника  

Построение правильного пятиугольника

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

 

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Вот один из методов построения правильного пятиугольника в заданной окружности:

  1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
  2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
  3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
  4. Постройте точку C посередине между O и B.
  5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
  6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
  7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
  8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
  9. Постройте правильный пятиугольник AEGHF.
  Пятиугольный узел на полоске бумаги

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.

Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

Интересные факты

См. также

Примечания

ru-wiki.org