Что называется живым сечением потока: Основы гидродинамики

3.5. Живое сечение. Смоченный периметр. Гидравлический радиус

В
гидравлических расчётах для характеристики
размеров и формы поперечного сечения
потока вводят понятие о живом
сечении и его элементах: смоченном
периметре и гидравлическом радиусе.

Живым
сечением
называется поверхность в пределах
потока, проведённая нормально к линиям
тока.

Для
круглого трубопровода, когда всё
поперечное сечение заполнено жидкостью,
живым сечение является площадь круга:

(рис.3.6).

Рис.
3.6. Элементы потока

Смоченным
периметром
называют ту часть периметра живого
сечения, по которой жидкость соприкасается
со стенками трубопровода (рис.3.6).
Смоченный периметр обычно обозначают
греческой
(хи). Для круглой трубы полностью
заполненной жидкостью смоченный периметр
равен длине окружности:

.

Гидравлическим
радиусом
называют отношение живого сечения к
смоченному периметру, т. е. величину

.

Эта
величина характеризует удельную, т.е.
приходящуюся на единицу длины смоченного
периметра, площадь живого сечения. Легко
сделать вывод, что поток с наибольшим
гидравлическим радиусом при прочих
равных условиях имеет минимальную силу
трения, приложенную к смоченной
поверхности.

Для
круглых труб, полностью заполненных
жидкостью, гидравлический радиус равен
четверти диаметра:

.

Введение
гидравлического радиуса как характерного
размера позволяет сравнивать по критерию
подобия (Re)
потоки с разными формами живого сечения.

Рассмотренные
основные понятия позволяют решать самые
различные практические задачи гидравлики.

Пример
3.1. Определить
скорость потока в трубопроводе. Диаметр
,
расход воды (несжимаемой жидкости) -.

Решение.
Искомая скорость
.

Определим
площадь живого сечения:

.

Скорость
потока:

.

Гидравлика
– это техническая механика жидкости,
в которой часто используются упрощённые
методы для решения инженерных задач.
Во многих случаях при решении практических
задач гидравлики удобно применять такие
центральные понятия механики, как
количество движения (уравнение импульсов)
и кинетическая энергия.

В
связи с этим необходимо рассмотреть
возможность вычисления количества
движения и кинетическую энергию потока
жидкости по средней скорости, а не по
действительным местным скоростям. Это
позволит существенно упростить
гидравлические расчёты.

Для
материального тела массой
,
движущегося со скоростью,
изменение количества движения за времявследствие действия силывыразится векторным уравнением

, (3.7)

где
— приращение количества движения,
обусловленное импульсом.

Жидкость
представляет собой материальную систему,
поэтому основной закон механики может
быть приложен к любой выделенной из неё
массе.

Применим
эту теорему механики к участку потока
жидкости с расходом
между сечениями 1-1 и 2-2 (выделенный
участок заштрихован). Ограничимся
рассмотрением только установившегося
движения жидкости (рис. 3.7).

За
время
этот участок переместится в положение,
определяемое сечениямии.
Объёмы этих элементов,
а, следовательно, и их массыодинаковы, поэтому приращение количества
движения будет равно

. (3.8)

Это
приращение количества движения
обусловлено импульсом всех внешних
сил, действующих на объём жидкости между
сечениями 1-1 и 2-2. Внешними силами,
приложенными к выделенному объёму,
являются сила тяжести всего объёма
,
силы давления в первом и втором сеченияхи(нормальные к этим сечениям и направленные
внутрь объёма), а также реакции стенок
трубы,
которая складывается из сил давления
и трения, распределённых по боковой
поверхности объёма.

Рис.
3.7. Применение уравнения количества
движения

к
потоку жидкости

Уравнение
импульсов (3.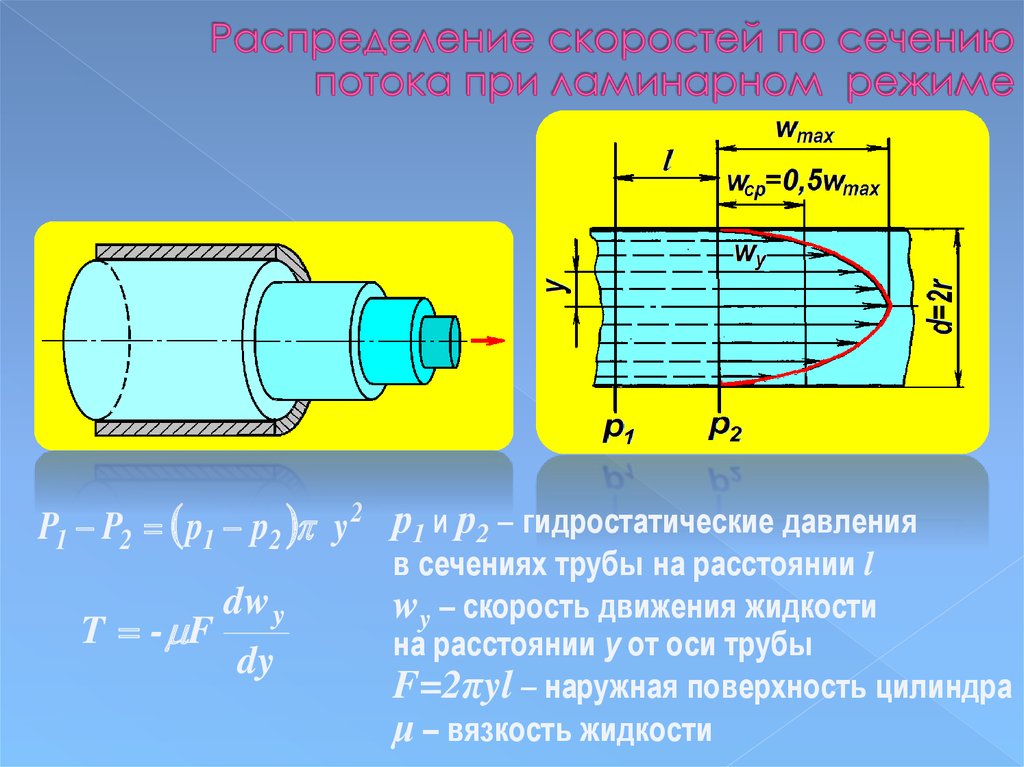 7) для рассматриваемого
случая можно записать в виде

.

После
сокращения на

. (3.9)

Составив
проекции этого векторного уравнения
на три координатные оси, получим три
алгебраических уравнения с тремя
неизвестными —
.

Л.
Эйлер предложил удобный графический
способ нахождения силы
.
Перенося в формуле (3.?) все слагаемые в
одну сторону, можно представить его в
виде суммы векторов:

=
0, (3.10)

где
вектор
взят с обратным знаком (т.е. по направлению
обратный действительному). В соответствии
с этим выражением (3.10) силуможно найти, построив замкнутый
многоугольник сил, как это показано на
рис. 3.7,а.

Анализ
показывает, что при вычислении количества
движения и кинетической энергии по
средней скорости допускается ошибка,
которую можно учесть с помощью двух
коэффициентов:

—
коэффициента Буссинеска
при вычислении количества движения;

—
коэффициента Кориолиса
в уравнении Бернулли при вычислении
кинетической энергии.

Величина
обоих коэффициентов зависит от характера
распределения скоростей в поперечном
сечении потока жидкости. На практике
при турбулентном режиме движения
коэффициент Кориолиса
, а коэффициент Буссинеска.
Поэтому обычно полагают.
Однако встречаются отдельные случаи,
когдадостигает больших значений, и тогда
пренебрежение им может привести к
значительным погрешностям.

Пример
3.2. Определить
силу воздействия потока жидкости на
преграду. Пусть жидкость вытекает в
атмосферу и наталкивается на безграничную
стенку, установленную нормально к
потоку. В результате жидкость растекается
по стенке, изменяя направление своего
течения на 90⁰
(рис.
3.8). Известны площадь сечения потока
,
скорость истеченияи плотность жидкости.

Рис. 3.8. Воздействие
струи на преграду

Для
решения данной задачи берём фиксированный
объём, показанный штриховой линией, и
применяем теорему Эйлера. Так как
давление внутри струи и по поверхности
жидкости равно атмосферному, т.е.
избыточное давление равно нулю, уравнение,
выражающее теорему Эйлера, для направления,
совпадающего с вектором скорости
истечения
,
будет иметь вид

,

или . (3.11)

Это
и есть сила воздействия потока жидкости
на преграду. При другом угле установке
стенки или других её форме и размерах
в правую формулы (3.11) вводится безразмерный
коэффициент, отличный от единицы, но
пропорциональность силы
произведениюсохранится.

15) Элементарная струйка, поток жидкости, живое сечение. Гидравлический радиус, расход и средняя скорость.

Часть
потока, заключенная
внутри трубки тока, называется элементарной
струйкой.
Поток
Ж
– представляет собой совокупность
элементарных струек.

Живым
сечением
– сечение потока Ж, перпендикулярное
направлению скорости ее сечения. При
плавно изменяющемся движении Ж сечение
считается плоским и равным площади
поперечного сечения потока ().

Площадь
живого сечения S=
dS

Расход
потока Q
— объем жидкости V,
протекающей за единицу времени t
через живое сечение ω.

Средняя
скорость потока υ
— скорость движения жидкости, определяющаяся
отношением расхода жидкости Q
к площади живого сечения ω

Гидравлический
радиус потока R
— отношение живого сечения к смоченному
периметру
Смоченный
периметр χ
(«хи») — часть периметра живого
сечения, ограниченное твердыми стенками.

16) Уравнение неразрывности. Понятие расхода.

Течение жидкости
называют стационарным,
если в каждой точке пространства,
занимаемого жидкостью, ее скорость с
течением времени не изменяется.Жидкости
практически несжимаемы,
т. е. можно считать, что данная масса
жидкости всегда имеет неизменный объем.
Поэтому одинаковость объемов жидкости,
проходящих через разные сечения трубы,
означает, что скорость течения жидкости
зависит от сечения трубы. Пусть скорости
стационарного течения жидкости через
сечения трубы S₁
и S₂
равны соответственно v₁
и v₂.
Объем жидкости, протекающей за промежуток
времени t через сечение S₁,
равен V₁=S₁v₁t,
а объем жидкости, протекающей за то же
время через сечение S2, равен V₂=S₂v₂t.
Из равенства V₁=V₂
следует, что
уравнением
неразрывности.
Из него следует, что
Следовательно, при стационарном течении
жидкости скорости движения ее частиц
через разные поперечные сечения трубы
обратно пропорциональны площадям этих
сечений.

Расходом
называется количество жидкости,
протекающее через живое течение потока
(струйки) в единицу времени. Различают
объёмный Q
(м³/с),
весовой Q_G(Н/с)
и массовый Q_m(кг/с)
расходы.

;

17) Распределение сил в сплошной среде. Объемные и поверхностные силы.

Внешние
силы: массовые
(объемные) и поверхностные.

Массовые
силы
в соответствии со вторым законом Ньютона
про­порциональны
массе жидкости или, для однородной
жидкости, — ее
объему. К ним относятся сила тяжести и
сила инерции переносного движения.

Поверхностные
силы
непрерывно распределены по поверхности
жидкости
и при равномерном их распределении
пропорциональны площади
этой поверхности.

Массо­вые
силы относят к единице мас­сы,
а поверхностные к единице площади

Сплошна́я
среда́ — механическая система, обладающая
бесконечным числом внутренних степеней
свободы. Её движение в пространстве, в
отличие от других механических систем,
описывается не координатами и скоростями
отдельных частиц, а скалярным полем
плотности и векторным полем скоростей.

Если
плотность сплошной среды постулируется
равной константе, то такая сплошная
среда называется несжимаемой.

18) Уравнение Бернулли для установившегося движения жидкости.

Напорная
линия – линия показывающая изменение
гидродинамического напора Ж по длине
потока

Линия,
соединяющая уровни Ж в пьезометрах
наз-ся пьезометрической линией

Отметим,
что в такой записи члены уравнения
выражают удельную энергию, отнесенную
к весу (Mg
= G).

Как
и в гидростатике, величину z называют высотой
положения, а
величину p/gρ
— пьезометрической высотой. 

Сумма
первых двух членов уравнения  z
+ p/gρ — пьезометрический напор. 

Третий
член уравнения u²/2g линейная
величина. Как известно, начавшаяся
двигаться вертикально со скоростью u при
отсутствии сопротивления движению,
поднялась бы на высоту u²/2g. Этот
член уравнения Бернулли называется скоростной
высотой или скоростным
напором.

Расход и его связь со скоростью

Цели обучения

К концу этого раздела вы сможете:

• Рассчитать расход.
• Определить единицы объема.
• Опишите несжимаемые жидкости.
• Объясните следствия уравнения неразрывности.

Скорость потока  Q определяется как объем жидкости, проходящей через какое-либо место через область в течение периода времени, как показано на рисунке 1. Символами это может быть записано как 9.0005

[латекс]Q=\frac{V}{t}\\[/латекс],

, где V — объем, а t — прошедшее время. Единицей СИ для расхода является м ³ /с, но широко используется ряд других единиц для Q . Например, сердце покоящегося взрослого человека перекачивает кровь со скоростью 5,00 литров в минуту (л/мин). Обратите внимание, что литров (л) составляет 1/1000 кубического метра или 1000 кубических сантиметров (10 ^-3 м ³  или 10 ³  см ³ ). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.

Рис. 1. Расход – это объем жидкости в единицу времени, протекающий через точку через площадь A . Здесь заштрихованный цилиндр жидкости течет мимо точки P по однородной трубе за время t . Объем цилиндра равен Ad  , а средняя скорость равна [латекс]\overline{v}=d/t\\[/latex], так что скорость потока равна [латекс]Q=\text{Ad}/t =A\overline{v}\\[/латекс] .

Пример 1. Расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь

Сколько кубометров крови перекачивает сердце за 75 лет жизни, при условии, что средняя скорость кровотока составляет 5,00 л/мин. ?

Стратегия

Время и расход Q даны, поэтому объем V можно рассчитать из определения расхода.

Решение

Решение 9{3}\end{массив}\\[/латекс].

Обсуждение

Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом Q и скорость [латекс]\bar{v}\\[/латекс] равна

[латекс]Q=A\overline{v}\\[/латекс],

, где A — площадь поперечного сечения, а [латекс]\bar{v}\\[/латекс] — средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. На рисунке 1 показано, как получается это соотношение. Заштрихованный цилиндр имеет объем

V = Ad,

который проходит через точку P за время t . Разделив обе части этого соотношения на t , мы получим

[латекс]\frac{V}{t}=\frac{Ad}{t}\\[/latex].

Заметим, что Q = V / t и средняя скорость [латекс]\overline{v}=d/t\\[/латекс]. Таким образом, уравнение принимает вид [латекс]Q=A\overline{v}\\[/латекс]. На рисунке 2 показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для пунктов 1 и 2,

[латекс]\begin{cases}Q_{1} &=& Q_{2}\\ A_{1}v_{1} &=&A_{2}v_{2} \end{cases}\\[/ латекс]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рис. 2. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)

Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример 2. Расчет скорости жидкости: скорость увеличивается при сужении трубы

Насадка радиусом 0,250 см присоединена к садовому шлангу радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для насадки. 9{2}}=1,96\text{ м/с}\\[/латекс].

Решение для (b)

Мы могли бы повторить этот расчет, чтобы найти скорость в сопле [латекс]\bar{v}_{2}\\[/латекс], но мы будем использовать уравнение неразрывности дать несколько иное представление. Используя уравнение, которое устанавливает

[латекс]{A}_{1}{\overline{v}}_{1}={A}_{2}{\overline{v}}_{2}\\[ /латекс],

решение для [латекс]{\overline{v}}_{2}\\[/латекс] и подстановка πr ² площади поперечного сечения дает 9{2}}1,96\text{ м/с}=25,5 \text{ м/с}\\[/латекс].

Обсуждение

Скорость 1,96 м/с подходит для воды, вытекающей из шланга без насадки. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно. Во многих ситуациях, в том числе и в сердечно-сосудистой системе, происходит разветвление течения. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но это сумма расходов в каждой из ветвей на любом участке обслуживаемой трубы. Уравнение непрерывности в более общем виде принимает вид

[латекс]{n}_{1}{A}_{1}{\overline{v}}_{1}={n}_{2}{A }_{2}{\overline{v}}_{2}\\[/latex],

, где n ₁ и n ₂ — количество ответвлений в каждом из участков вдоль трубка.

Пример 3. Расчет скорости кровотока и диаметра сосуда: разветвление в сердечно-сосудистой системе

Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра составляет 8,0  мкм м, рассчитайте количество капилляров в системе кровообращения. 9{2}}=0,27\text{ м/с}\\[/латекс].

Решение для (b)

Использование [латекса]{n}_{1}{A}_{1}{\overline{v}}_{1}={n}_{2}{A }_{2}{\overline{v}}_{1}\\[/latex], присвоив индекс 1 аорте и 2 капиллярам, ​​и найдя n ₂ (количество капилляров ) дает [латекс]{n}_{2}=\frac{{n}_{1}{A}_{1}{\overline{v}}_{1}}{{A}_{2} {\overline{v}}_{2}}\\[/латекс]. Преобразование всех величин в единицы метров и секунд и подстановка в приведенное выше уравнение дает 9{9}\text{капилляры}\\[/латекс].

Обсуждение

Обратите внимание, что скорость кровотока в капиллярах значительно снижена по сравнению со скоростью в аорте из-за значительного увеличения общей площади поперечного сечения капилляров. Эта низкая скорость должна дать достаточно времени для эффективного обмена, хотя не менее важно, чтобы поток не становился стационарным, чтобы избежать возможности свертывания крови. Кажется ли разумным такое большое количество капилляров в организме? В активной мышце находится около 200 капилляров на мм 9 .0035 3 , или около 200×10 ⁶ на 1 кг мышц. Для 20 кг мышц это составляет примерно 4 × 10 ⁹ капилляров.

Резюме раздела

• Скорость потока  Q   определяется как объем V  , протекающий через момент времени  t , или [latex]Q=\frac{V}{t}\\[/latex ] где V — объем, а t — время.
• Единица объема в системе СИ: м ³ .
• Другой распространенной единицей измерения является литр (л), который равен 10 ^-3 м ³ .
• Расход и скорость связаны соотношением [латекс]Q=A\overline{v}\\[/latex], где A  – площадь поперечного сечения потока, а [латекс]\overline{v}\\[ /латекс] — его средняя скорость.
• Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть

[латекс]\begin{cases}Q_{1} &=& Q_{2}\\ A_{1}v_{1} &=&A_{2}v_{2}\\ n_{1}A_{1 }\bar{v}_{1} &=& n_{2}A_{2}\bar{v}_{2}\end{case}\\[/latex].

Концептуальные вопросы

1. В чем разница между расходом и скоростью жидкости? Как они связаны?

2. На многих рисунках в тексте показаны линии тока. Объясните, почему скорость жидкости наибольшая там, где линии тока расположены ближе всего друг к другу. (Подсказка: рассмотрите взаимосвязь между скоростью жидкости и площадью поперечного сечения, через которое она течет. )

3. Назовите несжимаемые и несжимаемые вещества.

Задачи и упражнения

1. Каков средний расход бензина в см ³ /с в двигатель автомобиля, движущегося со скоростью 100 км/ч, если он составляет в среднем 10,0 км/л?

2. Сердце взрослого человека в состоянии покоя перекачивает кровь со скоростью 5,00 л/мин. (a) Преобразуйте это в см ³ /с. б) Чему равна эта скорость в м ³ /с?

3. Кровь перекачивается из сердца со скоростью 5,0 л/мин в аорту (радиусом 1,0 см). Определить скорость движения крови по аорте.

4. Кровь течет по артерии радиусом 2 мм со скоростью 40 см/с. Определить скорость кровотока и объем, проходящий через артерию за 30 с.

5. Водопад Хука на реке Вайкато — одна из самых посещаемых природных достопримечательностей Новой Зеландии (см. рис. 3). Средний расход реки составляет около 300 000 л/с. В ущелье река сужается до 20 м в ширину и достигает в среднем 20 м глубины. а) Какова средняя скорость течения реки в ущелье? б) Какова средняя скорость воды в реке ниже по течению от водопада, когда она расширяется до 60 м, а ее глубина увеличивается в среднем до 40 м?

Рис. 3. Водопад Хука в Таупо, Новая Зеландия, демонстрирует скорость потока. (кредит: RaviGogna, Flickr)

6. Основная артерия с площадью поперечного сечения 1,00 см ²  разветвляется на 18 более мелких артерий, каждая со средней площадью поперечного сечения 0,400 см ² . Во сколько раз уменьшается средняя скорость крови при переходе в эти ветви?

7. (a) Когда кровь проходит через капиллярное русло в органе, капилляры соединяются, образуя венулы (мелкие вены). При увеличении скорости крови в 4,00 раза и общей площади поперечного сечения венул 10,0 см ² , какова общая площадь поперечного сечения капилляров, питающих эти венулы? б) Сколько капилляров задействовано, если их средний диаметр составляет 10,0  мкм м?

8. Система кровообращения человека имеет примерно 1 × 10 ⁹  капиллярных сосудов. Каждый сосуд имеет диаметр около 8 мкм м. Предполагая, что сердечный выброс составляет 5 л/мин, определите среднюю скорость кровотока через каждый капиллярный сосуд.

9. (a) Оцените время, необходимое для наполнения частного бассейна вместимостью 80 000 л из садового шланга с расходом 60 л/мин. б) Сколько времени потребовалось бы для заполнения, если бы вы могли отвести реку среднего размера, текущую на высоте 5000 м 9 ?0035 3 /с, туда?

10. Скорость кровотока через капилляр радиусом 2,00×10 ^-6 -3,80×10 ⁹ . а) Какова скорость кровотока? (Эта небольшая скорость дает время для диффузии материалов в кровь и из крови.) (b) Если предположить, что вся кровь в организме проходит через капилляры, сколько их должно быть, чтобы обеспечить общий поток 90,0 см ³ / с? (Полученное большое число является завышенным, но все же разумным.)

11. (a) Какова скорость жидкости в пожарном шланге диаметром 9,00 см, по которому течет 80,0 л воды в секунду? б) Какова скорость потока в кубических метрах в секунду? (c) Были бы ваши ответы другими, если бы соленая вода заменила пресную воду в пожарном шланге?

12. Диаметр главного воздухозаборника калорифера нагнетательного газового 0,300 м. Какова средняя скорость воздуха в воздуховоде, если каждые 15 мин по нему проходит объем, равный внутреннему объему дома? Внутренний объем дома эквивалентен прямоугольному массиву шириной 13,0 м, длиной 20,0 м и высотой 2,75 м.

13. Вода движется со скоростью 2,00 м/с по шлангу с внутренним диаметром 1,60 см. а) Какова скорость потока в литрах в секунду? (b) Скорость жидкости в насадке этого шланга составляет 15,0 м/с. Какой внутренний диаметр сопла?

14. Докажите, что скорость движения несжимаемой жидкости через сужение, например, в трубе Вентури, увеличивается в кратном размере, равном квадрату множителя, в который уменьшается диаметр. (Обратное верно для вытекания из сужения в область большего диаметра.)

15. Вода течет прямо из крана диаметром 1,80 см со скоростью 0,500 м/с. (Из-за конструкции крана скорость потока не меняется.) а) Какова скорость потока в см ³ /с? б) Каков диаметр ручья на 0,200 м ниже крана? Эффектами поверхностного натяжения пренебречь.

16. Необоснованные результаты Горный ручей имеет ширину 10,0 м и среднюю глубину 2,00 м. В весенний период сток в ручье достигает 100 000 м ³ /с. а) Какова средняя скорость потока при этих условиях? б) Что неразумного в этой скорости? (c) Что является неразумным или непоследовательным в предпосылках?

Глоссарий

расход:

, сокращенно Q , это объем V , который проходит через определенную точку за время t , или Q = V/t

литр:

единица объема, равная 10 ⁻³ м ³

Избранные решения задач и упражнений

1. 2,78 см ³ /с

3. 27 см/с

5. (а) 0,75 м/с (б) 0,13 м/с

5

5 9 а) 40,0 см ²  (б) 5,09×10 ⁷

9. (а) 22 ч (б) 0,016 с

11. (а) 12,6 м/с (б) 003 6 0,09030 м 3 s (c) Нет, не зависит от плотности.

13. (a) 0,402 л/с (b) 0,584 см

15. (a) 128 см ³ /с (b) 0,890 см

 

12.1 Скорость потока и ее связь со скоростью – Колледж физики

Сводка

• Рассчитать скорость потока.
• Определить единицы объема.
• Опишите несжимаемые жидкости.
• Объясните следствия уравнения неразрывности.

Скорость потока определяется как объем жидкости, проходящей через какое-либо место через область в течение периода времени, как показано на рисунке 1. Символами это может быть записано как

где объем и прошедшее время.

Единица СИ для расхода – это всего лишь ряд других общеупотребительных единиц. Например, сердце покоящегося взрослого человека перекачивает кровь со скоростью 5,00 литров в минуту (л/мин). Обратите внимание, что литров (L) составляет 1/1000 кубического метра или 1000 кубических сантиметров (или ). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.

Рисунок 1. Расход – это объем жидкости в единицу времени, протекающий мимо точки через площадь А . Здесь заштрихованный цилиндр жидкости течет мимо точки P в однородной трубе за время t . Объем цилиндра равен Ad , а средняя скорость равна v̄=d/t , так что расход равен Q=Ad/t=Av̄ .

Пример 1. Расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь

Сколько кубометров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?

Стратегия

Заданы время и расход, поэтому объем можно рассчитать исходя из определения расхода.

Решение

Решение для объема дает

Подстановка известных значений дает

Обсуждение

Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом и скоростью составляет

где – площадь поперечного сечения, – средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. Рисунок 1 иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем

, которое проходит мимо точки во времени. Разделив обе части этого отношения на 9, получаем0005

Заметим, что и средняя скорость равна Таким образом уравнение становится

На рис. 2 показано течение несжимаемой жидкости по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для пунктов 1 и 2,

[размер латекса = ”4″]\rbrace[/латекс]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рисунок 2. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)

Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример 2. Расчет скорости жидкости: скорость увеличивается при сужении трубы

Насадка с радиусом 0,250 см прикреплена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для насадки.

Решение для (a)

Сначала мы находим и замечаем, что площадь поперечного сечения дает

Подстановка известных значений и выполнение соответствующих преобразований единиц дает

Решение для (b)

Мы могли бы повторите этот расчет, чтобы найти скорость в сопле, но мы будем использовать уравнение неразрывности, чтобы получить несколько иное представление. Используя уравнение, которое утверждает

, решая и подставляя площадь поперечного сечения, получаем

Подстановка известных значений,

Обсуждение

Скорость 1,96 м/с подходит для воды, вытекающей из шланга без насадки. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.

Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид

где и – количество ответвлений на каждом из участков по длине трубы.

Пример 3: расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе

Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что по среднему диаметру капилляра рассчитывают количество капилляров в системе кровообращения.

Стратегия

Мы можем использовать для расчета скорости кровотока в аорте, а затем использовать общую форму уравнения непрерывности для расчета количества капилляров, поскольку все остальные переменные известны.

Решение для (а)

Скорость потока указана для цилиндрического сосуда или для него.

Подстановка известных значений (преобразованных в единицы метров и секунд) дает

Решение для (b)

Использование присвоения нижнего индекса 1 аорте и 2 капиллярам и решение (количество капилляров) дает Преобразование всех величин в единицы метров и секунд и подстановка в приведенное выше уравнение дает

Обсуждение

Обратите внимание, что скорость кровотока в капиллярах значительно снижена по сравнению со скоростью в аорте из-за значительного увеличения общей площади поперечного сечения капилляров.