Как найти тангенс угла по клеточкам? Как искать тангенс угла
Как найти тангенс угла по клеточкам?
Найти тангенс угла по клеткам
Как по мне, то легче всего отложить прямую линию - так, чтобы образовался прямоугольный треугольник.
Здесь мы уже имеем кое-какую информацию. В прямоугольном треугольники тангенсом острого угла является отношение противоположного катета к прилежащему. Отсюда получается, что тангенс кута - это отложенная прямая линия разделенная на прилежащий катет.
Например, если прямая линия, которую мы проложили, будет длинной в 5 клеточек, а прилежащий катет длинной в одну, то 5/1 = 5. Или же если эта линия, которую мы провели, равняется, к примеру, 6, а прилежащий катет - 2, то 6/2=3. Вот такая простая арифметика, главное, понять суть вычислений и применять их на практике.
Найти тангенс ушла по клеточкам достаточно просто.
Допустим, у нас есть угол АОВ.
Из точки В мы опускаем вниз прямую. У нас получился треугольник с сторонами а и b.
Далее можно воспользоваться формулой: tg=b/a
Высчитываем по клеточкам длину сторон а и b. Получаем формулу tg=6/5. Получаем ответ 1,2.
Будем искать тангенс угла А треугольника АВС.
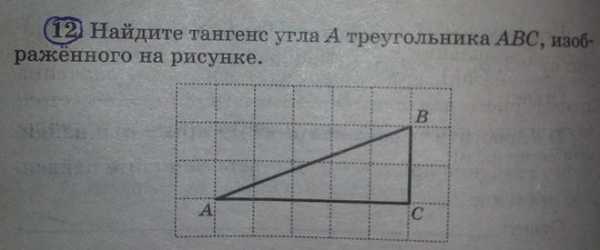
Решение.
Сначала посчитаем длину двух сторон данного треугольника, считать будем по клеточкам, и получим результат: АС=5 и ВС=2.
Тангенс угла А равен сторона ВС разделить на АС.
Подставляем в формулу, получаем тангенс угла А= 2/5=0,4
Вот так легко можно произвести вычисление.
Рассчитать тангенс угла по клеточкам довольно просто, если будешь знать формулу.
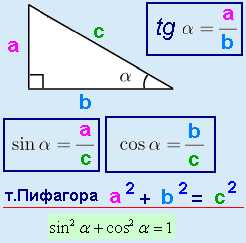
Тангенс является отношением противолежащего катета А к прилежащему катету Б.
Рассмотрим несколько примеров, как рассчитать тангенс именно по клеточкам.
В данном примере нужно найти тангенс угла АОВ.
Чуть сложнее пример.
Его решение.

Я слышала, что такого рода задания будут в ЕГЭ 2015 года. И сейчас учеников в школах учат находить тангенсы, синусы и косинусы угла по клеточкам.
Разберем тангенс угла треугольника:

Соединяем точка А и В, так чтобы стороны являлись гипотенузами:

Теперь по теореме Пифагора вычисляем все стороны, и получаем синус. А далее и косинус, тангенс и котангенс.
Вот решение:
Ответ: 11
Рассмотрим, как найти тангенс угла по клеточкам на конкретном примере.
Требуется найти тангенс угла АОВ.
Построим углы ХОА и ХОВ.
Тангенсы углов XOB и XOA можно сосчитать quot;по клеточкамquot; (для вычисления тангенса острого угла прямоугольного треугольника, надо найти отношение противолежащего катета к прилежащему):
A = tg (XOA) = 2/4 = 0.5
B = tg (XOB) = 3/1 = 3
tg (AOB) = tg (XOB - XOA) = (B - A/(1 + AB) = (3-0.5)/(1+0.5*3)=2.5/2.5=1
Тангенс угла найти по клеткам довольно легко. Для этого нужно посчитать клеточки и делить количество клеточек противолежащей стороны на количество клеточек прилежащей к углу стороны. Вот все, расчитывается это таким вот образом.
Давайте на примере найдм тангенс угла AOB, изображенного на рисунке ниже, по клеточкам:

Прочертив прямую линию, соединяющую две имеющихся по прямым углом, мы увидим прямоугольный треугольник:

В треугольнике ОВС образованный угол С является прямым.

Противолежащий катет ВС, ясно видно, что в 3 р. больше прилежащего катета ОС. Отсюда получаем, что tgAOB = BC : OC = 3
Ответ = 3
На самом деле, несмотря на всю мою любовь к точным наукам я не припомню, чтобы нас в школе учили рассчитывать тангенс, основываясь на количествах клеточек, на которых изображн угол.
Оказывается, это весьма увлекательное задание.
Предлагаю посмотреть один из вариантов расчта тангенса угла.

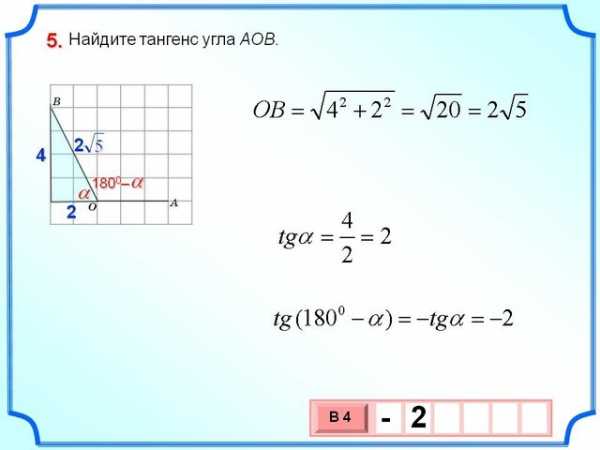
Чтобы найти тангенс угла необходимо построить угол обозначив две точки в тетрадке в клеточку или на миллиметровой бумаге, как написал Rafail, и соединить их прямой линией. Тогда угол между этой прямой и горизонталью будет заданным углом.
Как найти тангенс острого угла?
Вспомним школьный курс математики и поговорим о том, что такое тангенс и как найти тангенс угла. Сначала определим, что называется тангенсом. В прямоугольном треугольнике тангенсом острого угла является отношение противолежащего катета к прилежащему. Прилежащим катетом является тот, который участвует в образовании угла, противолежащим — тот, который расположен напротив угла.
Также тангенсом острого угла является отношение синуса этого угла к его косинусу. Для понимания напомним, что является синусом и косинусом угла. Синусом острого угла в прямоугольном треугольнике является отношение противолежащего катета к гипотенузе, косинус — это отношение прилежащего катета к гипотенузе.
Есть еще котангенс, он противоположен тангенсу. Котангенсом является отношение прилежащего катета к противолежащему и соответственно отношение косинуса угла к его синусу.
Синус, косинус, тангенс и котангенс являются тригонометрическими функциями угла, они показывают соотношения между углами и сторонами треугольника, помогают вычислять стороны треугольника.
Вычисляем тангенс острого угла
Как найти тангенс в треугольнике? Чтобы не тратить время на поиски тангенса, можно найти специальные таблицы, где указаны тригонометрические функции многих углов. В школьных задачках по геометрии очень распространены определенные углы, и значения их синусов, косинусов, тангенсов и котангенсов учителя просят запомнить. Мы предлагаем вам небольшую табличку с нужными значениями эти углов.

Если же угол, тангенс которого нужно найти, не представлен в этой таблице, то можно воспользоваться двумя формулами, которые мы и представили выше в словесной форме.
Первый способ вычислить тангенс угла — это поделить длину противолежащего катета на длину прилежащего. Допустим, противолежащий катет равен 4, а прилежащий 8. Чтобы
elhow.ru
Тангенс угла, теория и примеры
Определение и формула тангенса
ОПРЕДЕЛЕНИЕ Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего к этому углу катета к прилежащему катету. Тангенс угла обозначается .
Рассмотрим тригонометрическую окружность радиуса 1 с центром в начале координат.
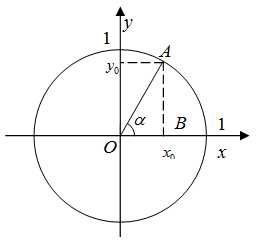
Выберем произвольный угол , которому на окружности соответствует точка . Опустим перпендикуляры на оси координат, тогда
т.е. тангенс угла это отношение ординаты точки А к абсциссе. Так как синус угла равен значению ординаты точки А, а косинус угла равен значению абсциссы, то
Функция периодическая с периодом , т.е.
Примеры решения задач
ПРИМЕР 1| Задание | В прямоугольном треугольнике с катетами см и см найти тангенсы углов и . |
| Решение | Так как тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то можем записать, что
|
| Ответ |
| Задание | Найти , если
|
| Решение | Преобразуем заданное выражение следующим образом:
или
Так как , то получаем, что
|
| Ответ |
Тангенс двойного угла
Тангенс половинного угла
График тангенса
Сумма тангенсов
Разность тангенсов
Тангенс суммы
Тангенс разности
Область определения тангенса
ru.solverbook.com
Таблица тангенсов, найти тангенс угла
Тангенс угла – одна из основных тригонометрических функций. Представляет собой соотношение катетов прямоугольного треугольника. То есть, tg(А)=ВС/АС, где ВС – противолежащий к углу (А) катет, АС – прилежащий катет.
Зачем необходимо знать тангенс угла? Такие данные имеют вполне практическое применение: в геодезии, мореходстве, авиации. Зная одну из сторон треугольника и угол, можно легко получить все остальные данные, используя тригонометрические тождества. Все расчеты легко производить с помощью онлайн-калькулятора на нашем сайте. Данные указаны в таблице тангенсов.
Для практического использования подходят не только таблицы Брадиса. Все тригонометрические функции вычисляются посредством калькулятора. Найдите красивое решение для вашей задачи.
Таблица тангенсов от 0° - 360°
|
|
|
|
|
|
|
|
|
|
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Смотрите также
allcalc.ru
Как найти угол по тангенсу
В комментариях к тригонометрической таблице меня спросили, как перевести в градусы tg@= 4,99237? В общем виде вопрос заключается в том, как найти угол по тангенсу? Для решения этой задачи мы будем использовать калькулятор. Поскольку математики никогда не ставили перед собой задачи навести порядок в математике, то углы и сегодня измеряются в самых разных единицах измерения. Наиболее популярны среди математиков градусная и радианная меры углов. Мы тоже найдем решение как в градусах, так и в радианах. Благо, на калькуляторе они есть.Сначала мы найдем угол по тангенсу в градусах. Для этого в правом верхнем углу калькулятора нужно установить специальный пыптик в положение Deg 360, что соответствует градусам. Дальше кнопочками вводим число 4,99237. Вот что у нас должно получиться.

После этого нужно нажать кнопочку арктангенс. Именно эта математическая ерунда превращает значение тангенса в угол. На калькуляторе эта хитрая обратная тригонометрическая функция (как её величают математики) замаскирована под кнопочку tan в степени минус 1, то есть тангенс в минус первой степени. После нажатия этой кнопочки восторженный калькулятор на все лады расхваливает нашу мудрость и всеми возможными способами сообщает нам, что мы таки ковырнули арктангенс, а не что нибудь другое. Об этом свидетельствует название функции atan (4.99237) в окошке калькулятора. Для особо одаренных здесь же буковками написано Arc tangent. Правда, особо одаренным нужно ещё знать английский язык, для того, чтобы понять всю глубину восторга калькулятора.

"А где же угол?" - спросите вы и будете правы. Угла нет, не смотря на все наши старания. Для превращения восторга калькулятора в математический результат нужно ещё нажать здоровенную кнопку равно, обозначенную двумя горизонтальными палочками =. Вот теперь мы нашли угол по тангенсу в градусах. Он равняется 78,6732 (ну, и так далее) градусов.
Для полного счастья, можно пролить бальзам на душу математиков, разложив эту десятичную форму записи градусов на градусы, минуты и секунды. Для этого дробную часть числа умножаем на 60 и получаем количество минут в дробном хвосте градусов.
0,6732 * 60 = 40,392'
Подобную процедуру повторяем с минутами. Дробную часть минут умножаем на 60 и получаем секунды.
0,392 * 60 = 23,52"
Процедуру можно повторять и дальше до бесконечности, но, к счастью, математики до этого ещё не додумались. По этому на секундах мы и остановимся. Ничего, что секунды у нас получились с дробным хвостиком. Математики к таким хвостам относятся терпимо. В итоге, полнометражная версия полученного нами угла в градусной мере углов выглядит следующим образом:
78 градусов 40' 23,52"
В слух эта магическая надпись произносится так: "78 градусов, 40 минут, 23 целых и 52 сотых секунды". Аминь!
Нет, ещё не "Аминь!". Теперь нужно выковырять из калькулятора этот же угол, только в радианах. Процедура добывания угла точно такая же, как и для градусов, с той только разницей, что в самом начале мы на калькуляторе нажимаем соседний пыптик Rad 2п. Повинуясь нашей воле, калькулятор добросовестно выдаст нам результат в радианах. Вот как это будет выглядеть.

Как видите, в радианах мы получили всего-навсего 1,3731 радиан. И за что математики так любят радианы? Ведь, плюнуть не на что. Ну, да Бог с ними, с этими математиками.
www.webstaratel.ru
Таблица тангенсов углов, вычислить тангенс угла
Современные определения тригонометрических функций и их символика принадлежат Л. Эйлеру. Хотя еще в 3-м в. до н. э в трудах Архимеда, Евклида и других рассматриваются отношения сторон в прямоугольном треугольнике, что фактически и является тригонометрическими функциями. В переводе с греческого тригонометрия означает «треугольник» и «измеряю» и является разделом математики, изучающим связь между сторонами и углами треугольника. Как нам известно, в прямоугольном треугольнике 2 угла острых, а один является прямым. Стороны треугольника, прилежащие к углу, равному 90 градусов, называются катетами, с сторона напротив прямого угла является гипотенузой. Тангенс представляет собой одну из тригонометрических функций угла. Функцию тангенс для острых углов можно рассматривать как отношение двух катетов: противолежащего к прилежащему.
tg (a)=а/в
где а — катет, противолежащий углу а;в — прилежащий катет.
Тангенс заданного угла можно определить, воспользовавшись таблицей Брадиса, где помещены тригонометрические функции всех углов. Если в задаче известна величина угла и одна из сторон треугольника, будет несложно определить остальные его стороны и углы. С помощью онлайн калькулятора ваши расчеты будут более быстрыми и правильными.Рассчитать тангенс угла
tg (°) =
Таблица тангенсов углов от 0° до 180°
|
|
|
Таблица тангенсов углов от 180° до 360°
|
|
|
infofaq.ru
Ищем тангенс угла. Методы определения данной характеристики на Kak-Legko.ru
Тангенс — это одна из тригонометрических функций. Изначально тригонометрические функции выражают зависимости элементов прямоугольных треугольников — сторон и углов. В прямоугольном треугольнике катеты — это стороны, образующие прямой угол, гипотенуза — третья сторона. Тогда тангенс угла — это отношение противолежащего катета к прилежащему. Таким образом, это безразмерная величина, т.е. она не измеряется в градусах или метрах, это просто число. Обозначается как tg. Для решения многих геометрических и математически задач требуется вычислить тангенс угла. Найти его можно разными способами.
Необходимо:
— калькулятор;— MS Excel;— базовые знания в области математики, геометрии и тригонометрии.
Инструкция:
- Данную величину можно определить как отношения синуса угла к косинусу этого же угла. Если они известны, то нужную характеристику можно вычислить по формуле tg(a)=sin(a)/cos(a).
- Значение можно вычислить с помощью инженерного калькулятора. Для этого наберите число и нажмите клавишу tg. Значение тангенса может быть сколь угодно большим или малым, но для значений углов, кратных 90 градусам, эта характеристика не существует.
- Значение tg можно определить по графику функции Y=tg(x). Для этого надо на оси X найти значение угла, для которого ищется данная характеристика, провести из этой точки перпендикуляр к оси абсцисс (ось ОX) до пересечения с графиком, затем из точки пересечения провести перпендикуляр к оси ординат (ось OY). Значение Y в этой точке и будет искомым значением тангенса.
- Как найти тангенс угла, если под рукой нет калькулятора? Можно посчитать его в программе Excel. Введите в любой ячейке =tan(радианы(а)), где а — число, от которого ищется значение характеристики, нажмите Enter. В ячейке появится значение данной величины.
- Также тригонометрические функции иногда определяют через ряды. Это позволяет вычислить их значение с любой точностью. Например, если разложить тангенс в ряд Тейлора, то первые члены этого ряда будут x+1/3*x^2+2/15*x^5+… Сумму этого бесконечно ряда можно посчитать, пользуясь свойствами пределов.
kak-legko.ru