Все формулы медианы прямоугольного треугольника. Как найти длину треугольника формула
Все формулы для треугольника
L - биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b - стороны треугольника
с - сторона на которую опущена биссектриса
d, e - отрезки полученные делением биссектрисы
γ - угол ABC, разделенный биссектрисой пополам
p - полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L - биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b - катеты прямоугольного треугольника
с - гипотенуза
α - угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L - биссектриса, отрезок ME , исходящий из острого угла
a, b - катеты прямоугольного треугольника
с - гипотенуза
α, β - углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L - высота=биссектриса=медиана
a - одинаковые стороны треугольника
b - основание
α - равные углы при основании
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты= биссектрисы= медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L - высота=биссектриса=медиана
a - стороны треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана - отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам. Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M - медиана, отрезок |AO|
c - сторона на которую ложится медиана
a , b - стороны треугольника
γ - угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам. Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M - медиана
R - радиус описанной окружности
O - центр описанной окружности
с - гипотенуза
a, b - катеты
α - острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Высота- перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом). Высоты треугольника пересекаются в одной точке, которая называется - ортоцентр.
H - высота треугольника
a - сторона, основание
b. c - стороны
β, γ - углы при основании
p - полупериметр, p=(a+b+c)/2
R - радиус описанной окружности
S - площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр - точка пересечения высот, совпадает с вершиной прямого угла.
H - высота из прямого угла
a, b - катеты
с - гипотенуза
c1 , c2 - отрезки полученные от деления гипотенузы, высотой
α, β - углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c - стороны произвольного треугольника
α, β, γ - противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
*Внимательно, при подстановке в формулу, для тупого угла ( α>90), сosα, принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Вычислить длину неизвестной стороны через любые стороны и углы
b - сторона (основание)
a - равные стороны
α - углы при основании
β - угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Есть следующие формулы для определения катета или гипотенузы
a, b - катеты
c - гипотенуза
α, β - острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (c, a, b):
zdesformula.ru
Все формулы высоты треугольника
Высота- перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется - ортоцентр.
H - высота треугольника
a - сторона, основание
b, c - стороны
β, γ - углы при основании
p - полупериметр, p=(a+b+c)/2
R - радиус описанной окружности
S - площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
Подробности Автор: Administrator Опубликовано: 09 октября 2011 Обновлено: 16 мая 2017
www-formula.ru
Все формулы для треугольника
Геометрия. Планиметрия
Формулы для произвольного треугольника
к содержанию справочника
- Медиана треугольника.
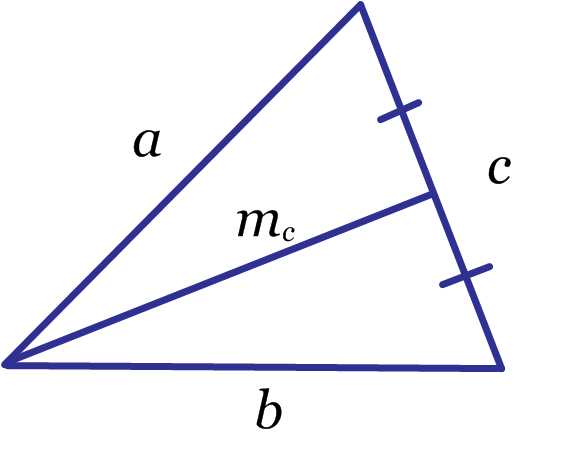Обратите внимание, что медиана проведена именно к стороне . - Биссектриса треугольника.
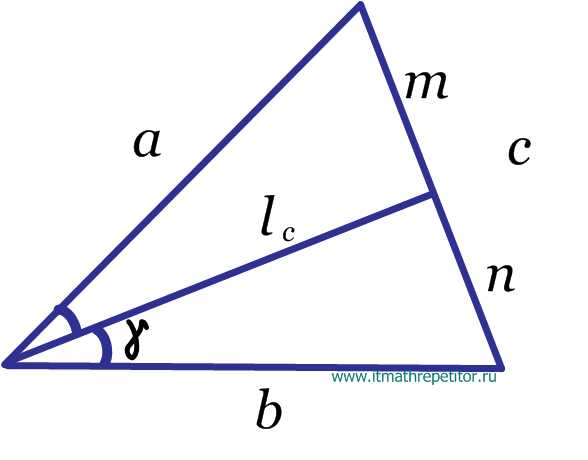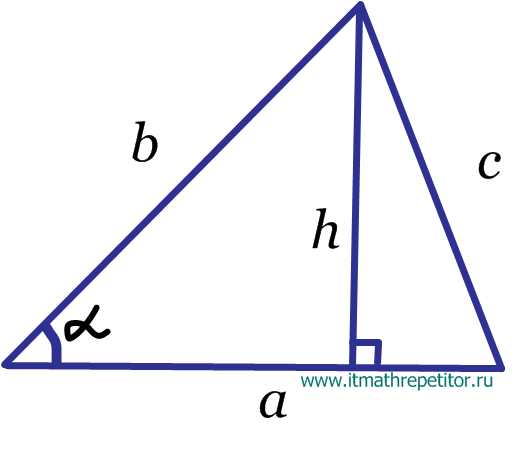
Обратите внимание, что биссектриса проведена именно к стороне - Теорема косинусов.
- Теорема синусов.
(следствие)
- Площадь треугольника.
(формула Герона),где (полупериметр)
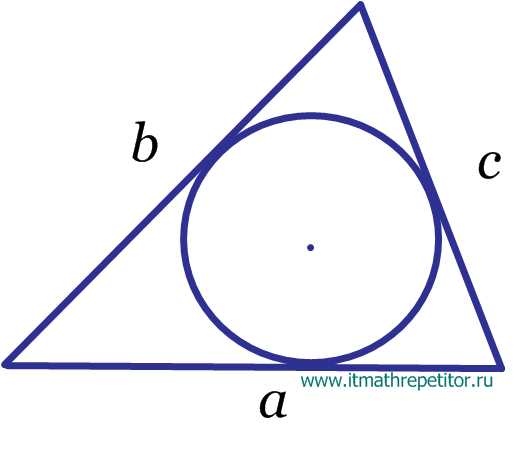
- Радиус вписанной окружности.
, где
(периметр)
- Радиус описанной окружности.
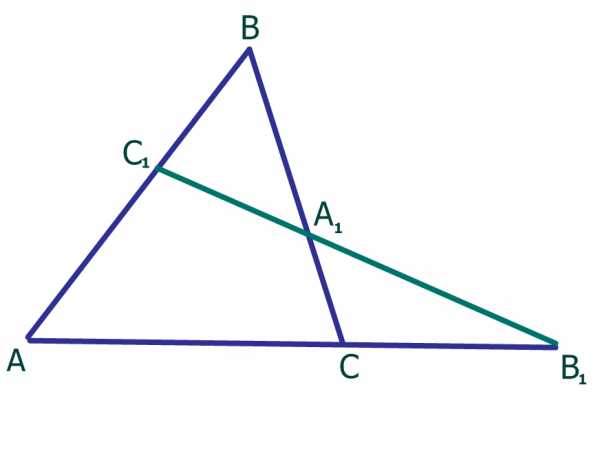
- Теорема Менелая.
Метки треугольник. Смотреть запись.
www.itmathrepetitor.ru
Все формулы медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M - медиана
R - радиус описанной окружности
O - центр описанной окружности
с - гипотенуза
a, b - катеты
α - острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Подробности Автор: Administrator Опубликовано: 08 октября 2011 Обновлено: 16 мая 2017
www-formula.ru
Все формулы сторон прямоугольного треугольника
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.
a, b - катеты
c - гипотенуза
α, β - острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Подробности Автор: Administrator Опубликовано: 12 октября 2011 Обновлено: 26 сентября 2017
www-formula.ru
Как найти стороны прямоугольного треугольника? Основы геометрии
Катеты и гипотенуза – стороны прямоугольного треугольника. Первые – это отрезки, которые прилегают к прямому углу, а гипотенуза является самой длинной частью фигуры и находится напротив угла в 90о. Пифагоровым треугольником называется тот, стороны которого равны натуральным числам; их длины в таком случае имеют название «пифагорова тройка».
Египетский треугольник
Для того чтобы нынешнее поколение узнало геометрию в том виде, в котором ее преподают в школе сейчас, она развивалась несколько веков. Основополагающим моментом считается теорема Пифагора. Стороны прямоугольного треугольника (фигура известна на весь мир) составляют 3, 4, 5.
Мало кто не знаком с фразой «Пифагоровы штаны во все стороны равны». Однако на самом деле теорема звучит так: c2 (квадрат гипотенузы) = a2+b2 (сумма квадратов катетов).
Среди математиков треугольник со сторонами 3, 4, 5 (см, м и т. д.) называется "египетским". Интересно то, что радиус окружности, которая вписана в фигуру, равняется единице. Название возникло примерно в V столетии до н.э., когда философы Греции ездили в Египет.
При построении пирамид архитекторы и землемеры пользовались соотношением 3:4:5. Такие сооружения получались пропорциональными, приятными на вид и просторными, а также редко рушились.
Для того чтобы построить прямой угол, строители использовали веревку, на которой было завязано 12 узлов. В таком случае вероятность построения именно прямоугольного треугольника повышалась до 95%.
Признаки равенства фигур
- Острый угол в прямоугольном треугольнике и большая сторона, которые равны тем же элементам во втором треугольнике, – бесспорный признак равенства фигур. Беря во внимание сумму углов, легко доказать, что вторые острые углы также равны. Таким образом, треугольники одинаковы по второму признаку.
- При наложении двух фигур друг на друга повернем их таким образом, чтобы они, совместившись, стали одним равнобедренным треугольником. По его свойству стороны, а точнее, гипотенузы, равны, так же как и углы при основании, а значит, эти фигуры одинаковые.
По первому признаку очень просто доказать то, что треугольники действительно равны, главное, чтобы две меньшие стороны (т. е. катеты) были равными между собой.
Треугольники будут одинаковыми по II признаку, суть которого заключается в равенстве катета и острого угла.
Свойства треугольника с прямым углом
Высота, которую опустили из прямого угла, разбивает фигуру на две равные части.
Стороны прямоугольного треугольника и его медианы легко узнать по правилу: медиана, которая опущена на гипотенузу, равна ее половине. Площадь фигуры можно найти как по формуле Герона, так и по утверждению, что она равна половине произведению катетов.
В прямоугольном треугольнике действуют свойства углов в 30о, 45о и 60о.
- При угле, который равен 30о, следует помнить, что противолежащий катет будет равен 1/2 самой большой стороны.
- Если угол 45о, значит, второй острый угол также 45о. Это говорит о том, что треугольник равнобедренный, и его катеты одинаковы.
- Свойство угла в 60о заключается в том, что третий угол имеет градусную меру в 30о.
Площадь легко узнать по одной из трех формул:
- через высоту и сторону, на которую она опускается;
- по формуле Герона;
- по сторонам и углу между ними.
Стороны прямоугольного треугольника, а точнее катеты, сходятся с двумя высотами. Для того чтобы найти третью, необходимо рассматривать образовавшийся треугольник, и тогда по теореме Пифагора вычислить необходимую длину. Помимо этой формулы существует также соотношение удвоенной площади и длины гипотенузы. Наиболее распространенным выражением среди учеников является первое, так как требует меньше расчетов.
Теоремы, применяемые к прямоугольному треугольнику
Геометрия прямоугольного треугольника включает в себя использование таких теорем, как:
- Теорема Пифагора. Ее суть заключается в том, что квадрат гипотенузы равен сумме квадратов катетов. В евклидовой геометрии данное соотношение является ключевым. Использовать формулу можно, если дан треугольник, к примеру, SNH. SN – гипотенуза, и ее необходимо найти. Тогда SN2=Nh3+HS2.
- Теорема косинусов. Обобщает теорему Пифагора: g2=f2+s2-2fs*cos угла между ними. Например, дан треугольник DOB. Известны катет DB и гипотенуза DO, необходимо найти OB. Тогда формула принимает данный вид: OB2=DB2+DO2-2DB*DO*cos угла D. Существует три следствия: угол треугольника будет остроугольным, если из суммы квадратов двух сторон вычесть квадрат длины третьей, полученный результат должен быть меньше нуля. Угол – тупоугольный, в том случае, если данное выражение больше нуля. Угол – прямой при равенстве нулю.
- Теорема синусов. Она показывает зависимость сторон к противолежащим углам. Иными словами, это отношение длин сторон к синусам противолежащих углов. В треугольнике HFB, где гипотенузой является HF, будет справедливо: HF/sin угла B=FB/sin угла H=HB/sin угла F.
fb.ru
100 формул / Все формулы площади треугольника
Через основание и высоту
\(S= \frac{1}{2} ah \)
\(S\) — площадь треугольника \(a\) — сторона \(h\) — высота опущенная на стороне \(a\)
Через две стороны и угол между ними
\(S= \frac{1}{2} ab sin \alpha \)
\(S\) — площадь треугольника \(a\) — сторона \(b\) — сторона \( \alpha \) — угол между сторонами \(a\) и \(b\)
Формула Герона
\(S= \sqrt{p(p-a)(p-b)(p-c)} \)
\(S\) — площадь треугольника \(a\) — сторона \(b\) — сторона \(c\) — сторона \(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
Через радиус вписанной окружности
\(S= rp \)
\(S\) — площадь треугольника \(r\) — радиус вписанной окружности \(a\) — сторона \(b\) — сторона \(c\) — сторона \(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
Через радиус описанной окружности
\(S= \frac{abc}{4R} \)
\(S\) — площадь треугольника \(R\) — радиус описанной окружности \(a\) — сторона \(b\) — сторона \(c\) — сторона
Площадь прямоугольного треугольника
\(S= \frac{1}{2} ab \)
\(S\) — площадь треугольника \(a\) — сторона \(b\) — сторона
\(S= de \) \(S\) — площадь треугольника
Формула Герона для прямоугольного треугольника
\(S= (p-a)(p-b) \)
\(S\) — площадь треугольника \(a\) — сторона \(b\) — сторона \(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
Площадь равнобедренного треугольника
\(S= \frac{1}{2} a^2 sin \alpha \)
\(S\) — площадь треугольника \(a\) — боковая сторона \(\alpha\) — угол между боковыми сторонами
\(S= \frac{1}{2} ab sin \alpha \)
\(S\) — площадь треугольника \(a\) — боковая сторона \(b\) — основание \(\alpha\) — угол между боковыми сторонами и основанием
\(S= \frac{b^2}{4tg \frac{ \alpha }{2}} \)
\(S\) — площадь треугольника \(a\) — боковая сторона \(b\) — основание \(\alpha\) — угол между боковыми сторонами и основанием
Площадь равностороннего треугольника
\(S= \frac{ \sqrt{3}a^2}{4} \)
\(S\) — площадь треугольника \(a\) — сторона
\(S= \frac{3 \sqrt{3}R^2}{4} \)
\(S\) — площадь треугольника \(R\) — радиус описанной окружности
\(S= 3 \sqrt{3}r^2 \)
\(S\) — площадь треугольника \(r\) — радиус вписанной окружности
\(S= \frac{h^2}{\sqrt{3}} \)
\(S\) — площадь треугольника \(h\) — высота
100formul.ru
