Число простых делителей числа. Сколько делителей имеет простое число? Как найти простые делители числа
Число простых делителей числа. Сколько делителей имеет простое число?
Каждый школьник знает, что все числа делятся на простые и составные. Более того, тем, кто усердно изучает математику, известны и их свойства. Однако если ответ на вопрос, сколько делителей имеет простое число, скрыт в самом определении этого понятия, то выяснить количество простых делителей для заданного — достаточно сложная задача. Она решается с применением метода перебора и вероятностных алгоритмов, реализуемых на ЭВМ.

Немного истории
Достоверно известно, что серьезным изучением свойств простых чисел первыми стали заниматься древние греки. Однако об их существовании было известно за несколько тысячелетий до того, как Аристотель включил теоремы об их свойствах в свои знаменитые “Начала”. Древние греки придумали и решето Эратосфена, представляющее собой алгоритм нахождения простых чисел из промежутка [1,n].
В 17 веке прорыв в их изучении сделали Пьер Ферма и Марен Мерсенн. Первый сформулировал теорему, впоследствии названную его именем, согласно которой все числа вида 22n — простые, доказав ее для n =1..4. Однако впоследствии Леонардом Эйлером было показано, что при n=5 получается составное число. Параллельно с этим Марен Мерсенн выделил простые числа вида 2p - 1, в которых p – простое. Они интересны тем, что для них легко проверить соответствие критерию простоты. Учитывая этот факт, числа Мерсенна используют для выявления сверхбольших простых чисел. На данный момент предельное из известных выглядит как 277232917 − 1 .
Кроме того, их широко используют при создании генераторов случайных чисел, имеющих широкое применение на практике.
Большую роль в исследовании простых чисел сыграли также Лежандр и Гаусс. Эти ученые выдвинули гипотезу об их плотности.

Решето Эратосфена
Если можно сразу же назвать простые делители числа 4, то для больших чисел сделать это обычно достаточно затруднительно. О решении этой проблемы люди стали задумываться еще несколько тысячелетий назад. В частности, древнегреческий математик Эратосфен, живший на стыке третьего и второго веков до Рождества Христова придумал алгоритм нахождения всех простых чисел, меньших целого числа n.
Он получил название решета, так как «просеивает» или по-современному «фильтрует» все числа, кроме простых.
Алгоритм состоит из следующих команд:
- выписать все целые числа от 2 до n;
- присвоить переменной p значение 2, так как это наименьшее простое число;
- зачеркнуть в списке все числа от 2p до n, кратные p;
- присвоить значению переменной p значение первого, не зачеркнутого числа записанной последовательности, которое большее p;
- повторять 3-й и 4-й, пока возможно.
Если все сделано правильно, то в списке останутся не зачеркнутыми все простые числа от двух до n.
Для реализации решета Эратосфена на электронно-вычислительной машине используют модернизированный алгоритм. На 3-м шаге можно зачеркивать числа, начиная с числа p2, так как все составные числа, которые меньше него, к этому времени уже будут зачеркнуты. Тогда остановка работы алгоритма должна произойти, когда выполнится условие p2>n.
Следует также учесть, что все простые числа, за исключением двойки, — нечетные, поэтому, начиная с p2 можно «фильтровать» по 2p.

Основная теорема арифметики
Согласно определению, простое число имеет два делителя. Один из них — 1, а второй — сама эта величина.
Прежде чем выяснить, каково число простых делителей числа, стоит уделить немного времени изучению основной теоремы арифметики. Согласно ей, натуральное число n > 1 можно представить, как n = p1*… ⋅*pk, где p1, … , pm — простые числа. При этом такое представление является единственным с точностью до порядка следования его сомножителей.
Следствие этой теоремы можно сформулировать следующим образом: любое натуральное число n представимо в виде n = p1d1*p2d2 * …* pkdm (в другой формулировке: каноническое разложение числа n на простые сомножители имеет вид n = p1d1*p2d2*⋅ …⋅*pkdm), где p1<p2< … <pm — простые числа, и d1, … , dm— некоторые натуральные числа.
Кроме того, уже известную вам основную теорему арифметики можно перефразировать следующим образом: любое каноническое разложение n можно считать тождественным, если не обращать внимания на порядок делителей. Это значит, что на практике для значительной части чисел существует множество достаточно простых алгоритмов их разложения на простые множители, которые в итоге дают один и тот же результат.
Критерий простоты
Прежде чем выяснить, как можно найти наибольший простой делитель числа (НПД) n, следует разобраться с другим важным вопросом.
Итак, выясним, по какому алгоритму можно установить, есть ли у величины другие делители кроме единицы и его самого.
Сделать это можно путем перебора простых чисел p1, …pk. Причем завершить цикл можно, как только pi+1, для которого производилась проверка, будет удовлетворять условию (pi+1)2> n.
Дадим объяснение, почему перебор можно ограничить pi>=sqr(n).
Предположим, у числа n, исследуемого на простоту есть некоторый делитель p. Тогда d=n/p так же будет его делителем. Но, так как d и p — разные числа, ни один из них не может быть больше корня из n.

Как найти наибольший простой делитель числа n
Найти НПД n, можно, действуя по следующей схеме:
- Разделить n на два, если оно четное или на три, если нечетное. Исключение составляет n, последняя цифра в десятичной записи которого ноль или пять. Такое число можно сразу разделить на пять.
- Если результат не целое число, то делят n на следующие целые числа, перебирая их вплоть до pi>=sqr(n).
Над получившимся числом n1 производят все действия, в том же порядке, что представлен выше, только с условием pi>=sqr(n1).
Если же ни на одном из шагов перебора n1 не делится на одно из простых чисел, то n целое и является своим же НПД. В противном случае получаем n2 и продолжаем деление с перебором до момента, когда на (i+1) шаге установим, что ni — целое.
Пример
Найдем простые делители числа 276.
- делим на "два";
- получаем 138;
- так как число четное, то вновь делим на "два";
- результат — 69;
- делим на следующее простое число "три";
- получаем 23.
Так как это число простое, можем подвести итог. Простыми делителями 276 являются 2, 3 и 23.
Как найти число простых делителей числа
Если речь идет о целом малом числе, то решение такой задачи не представляет никакой сложности. Рассмотрим конкретный пример. Найдем простые делители числа 54.
Для этого:
- 54 делим на "два" и получаем 27;
- 27 нечетное, поэтому разделим его уже не на "два", а на следующее простое число, т. е. "три";
- заметим, что 27=33;
- таким образом, разложение 54 имеет вид 54 = 21 * 33, т.е. простые делители числа 54 — это "два" и "три".
Однако это не все, что мы хотели знать. Теперь найдем число простых делителей числа 54. Оно равно произведению степеней простых множителей канонического разложения числа n = p1*d1 p2d2*⋅ …⋅*pmdm, увеличенных на 1. Иными словами, в общем случае K = (d1+1)*...* (dm+1).
Тогда для 54 имеем К = 2 * 4 = 8, т. е. общее число делителей равно восьми.
Обратите внимание, что все значительно упростилось, если бы речь шла о 23, 37, 103 и пр., так как каждый знает, сколько делителей у простого числа.

Пример
Найти число простых делителей числа 9990.
- так как число 9990 заканчивается на цифру "ноль", то оно делится на пять и на два.
- имеем 999.
- в результате деления на три имеем 333;
- снова делим на три, получаем 111;
- делим на три, имеем 37;
- 37 простое число, так как не делится без остатка ни на одно из простых чисел, которые находятся между двойкой и корнем из числа 37;
- подсчитываем количество простых делителей числа 9990. Это 2,3,5 и 37, то есть всего их четыре.
Проблема больших чисел
Как не странно, задача нахождения всех простых множителей числа является достаточно сложной. Дело в том, что до сих пор мы рассматривали только числа, десятичная запись которых состояла из одного-четырех знаков. Для них все вычисления выполняются в несколько шагов и их вполне можно осилить, имея под рукой лишь ручку и лист бумаги. По-другому обстоит дело, когда речь идет о, например, 1000-значном числе. Чтобы найти все его простые множители потребуется больше миллиарда лет, если даже будет задействован самый мощный суперкомпьютер в мире.
Простые числа и защита информации
Каждый современный человек, который пользуется возможностями, которые возникли благодаря появлению локальных компьютерных сетей и Интернета, нуждается в защите конфиденциальности своих личных данных, электронной переписки и пр. С этой целью используются криптографические алгоритмы с открытым ключом.
В системах с десятками и сотнями пользователей управление ключами является серьезной проблемой. Чтобы предотвратить овладение злоумышленником ключевой информацией, необходимо введение в процесс шифрования некой случайной величины.
Для этой цели наиболее распространенные на данный момент алгоритмы RSA используют большие простые числа.
Существует всего 10151 простых чисел длиною 1 - 512 битов включительно. В то же время для чисел, которые близки к n, вероятность того факта, что случайно выбранное число будет простым, — 1/ln n. Таким образом, полное количество простых чисел, которые меньше n равно n/ln n. Это позволяет считать, что крайне маловероятно, что 2 человека выберут одно и то же большое простое число.
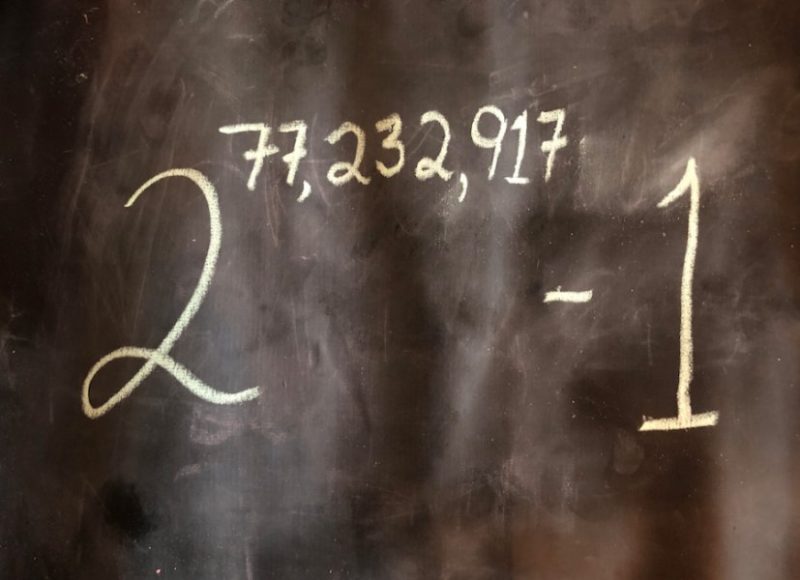
Тест Миллера — Рабина
В криптографических целях часто используют именно этот вид определения простоты числа, который имеет несколько модификаций.
Тест Миллера—Рабина основан на проверке ряда условий, выполняемых для чисел, которые делятся только на 1 и на самих себя. Если хотя бы одно из требований нарушено, это «экзаменуемое» число признается составным.
Для данного m находятся целые нечетное число t и s, такие чтобы выполнялось условие m-1=2st.
Затем выбирается случайное число a, такое что 1<a<m. Если a не свидетельствует о простоте числа m, то программа должна выдать ответ «m составное» и завершить свою работу. В противном случае выбирается другое случайное число a и проверка повторяется снова. После того как будут установлены r свидетелей простоты, должен быть выдан ответ «m, вероятно, простое», и алгоритм завершит свою работу.
Следствием теоремы Рабина является тот факт, что если r чисел, которые выбраны случайно, признаны свидетелями для определения простоты числа m, то вероятность того, что оно составное, не может превосходить (4-r).

Теперь вы знаете, сколько делителей имеет простое число и как выяснить наиболее примитивный алгоритм вычисления НПД. Эти знания помогут вам в решении многих практических задач.
fb.ru
Разложение числа на простые множители онлайн
Любое натуральное число можно представить в виде произведения простых чисел. Это представление называется разложением числа
можно представить в виде произведения простых чисел. Это представление называется разложением числа  на простые множители.
на простые множители.Натуральное число  называется делителем целого числа
называется делителем целого числа 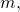 если для подходящего целого числа
если для подходящего целого числа  верно равенство
верно равенство 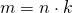
 делится на
делится на  или что число
или что число  кратно числу
кратно числу  .
.Простым числом называют натуральное число  , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей (любое натуральное число
, делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей (любое натуральное число 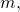 не равное
не равное  имеет как минимум два делителя:
имеет как минимум два делителя: 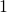 и
и  ). Например, числа
). Например, числа 

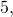

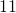 – простые, а числа
– простые, а числа 
 – составные.
– составные.
 большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.
большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.Данная программа раскладывает число в произведение простых множителей онлайн. Разложить число на множители онлайн с её помощью очень просто.
Как разложить число на множители?
В школе на уроках математики разложение числа на множители обычно записывают столбиком (в две колонки). Делается это так: в левую колонку выписываем исходное число, затем
- Берём самое маленькое простое число — 2 и по признакам делимости или обычным делением проверяем, делится ли исходное число на 2.
- Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую колонку под исходным числом.
- Если не делится, то берём следующее простое число — 3.
Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение заканчивается, когда в левой колонке будет записано число 1.
Чтобы лучше понять алгоритм, разберём несколько примеров.
Пример. Разложить на множители число 84.Решение. Записываем число 84 в левую колонку:
Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2, то и 84 делится на 2 по признаку делимости. Записываем 2 в правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:
Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число 21 записываем в левую колонку.
Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3, 21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили
Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:
Всё, число разложено!
В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.
О калькуляторе
Программа раскладывает числа на множители методом перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие числа. Однако если число простое или имеет большие простые делители, разложение его на множители происходит очень медленно.
umath.ru
Содержание
Вам понадобится
Инструкция
|
completerepair.ru
Как найти наибольший общий делитель (НОД)
Рассмотрим два способа нахождения наибольшего общего делителя.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.
Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.
Пример 1. Найдём НОД (84, 90).
Раскладываем числа 84 и 90 на простые множители:
Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой: 1 · 2 · 3 = 6.
Таким образом, НОД (84, 90) = 6.
Пример 2. Найдём НОД (15, 28).
Раскладываем 15 и 28 на простые множители:
Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель – единица.
НОД (15, 28) = 1.
Алгоритм Евклида
Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.
Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.
Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.
Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно, НОД (27, 9) = 9.
В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:
- Из двух данных чисел большее число делят на меньшее.
- Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
- Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
- Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
- Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.
Пример 2. Найдём наибольший общий делитель чисел 140 и 96:
1) 140 : 96 = 1 (остаток 44)
2) 96 : 44 = 2 (остаток 8)
3) 44 : 8 = 5 (остаток 4)
4) 8 : 4 = 2
Последний делитель равен 4 – это значит, что НОД (140, 96) = 4.
Последовательное деление так же можно записывать столбиком:
Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
- Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
- Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
- Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.
Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа – 48:
1) 48 : 4 = 12
48 делится на 4 без остатка. Таким образом, НОД (140, 96, 48) = 4.
naobumium.info
Содержание
Вам понадобится
Инструкция
|
completerepair.ru
Число простых делителей числа. Сколько делителей имеет простое число?
Образование 13 января 2018Каждый школьник знает, что все числа делятся на простые и составные. Более того, тем, кто усердно изучает математику, известны и их свойства. Однако если ответ на вопрос, сколько делителей имеет простое число, скрыт в самом определении этого понятия, то выяснить количество простых делителей для заданного — достаточно сложная задача. Она решается с применением метода перебора и вероятностных алгоритмов, реализуемых на ЭВМ.

Немного истории
Достоверно известно, что серьезным изучением свойств простых чисел первыми стали заниматься древние греки. Однако об их существовании было известно за несколько тысячелетий до того, как Аристотель включил теоремы об их свойствах в свои знаменитые “Начала”. Древние греки придумали и решето Эратосфена, представляющее собой алгоритм нахождения простых чисел из промежутка [1,n].
В 17 веке прорыв в их изучении сделали Пьер Ферма и Марен Мерсенн. Первый сформулировал теорему, впоследствии названную его именем, согласно которой все числа вида 22n — простые, доказав ее для n =1..4. Однако впоследствии Леонардом Эйлером было показано, что при n=5 получается составное число. Параллельно с этим Марен Мерсенн выделил простые числа вида 2p - 1, в которых p – простое. Они интересны тем, что для них легко проверить соответствие критерию простоты. Учитывая этот факт, числа Мерсенна используют для выявления сверхбольших простых чисел. На данный момент предельное из известных выглядит как 277232917 − 1 .
Кроме того, их широко используют при создании генераторов случайных чисел, имеющих широкое применение на практике.
Большую роль в исследовании простых чисел сыграли также Лежандр и Гаусс. Эти ученые выдвинули гипотезу об их плотности.

Решето Эратосфена
Если можно сразу же назвать простые делители числа 4, то для больших чисел сделать это обычно достаточно затруднительно. О решении этой проблемы люди стали задумываться еще несколько тысячелетий назад. В частности, древнегреческий математик Эратосфен, живший на стыке третьего и второго веков до Рождества Христова придумал алгоритм нахождения всех простых чисел, меньших целого числа n.
Он получил название решета, так как «просеивает» или по-современному «фильтрует» все числа, кроме простых.
Алгоритм состоит из следующих команд:
- выписать все целые числа от 2 до n;
- присвоить переменной p значение 2, так как это наименьшее простое число;
- зачеркнуть в списке все числа от 2p до n, кратные p;
- присвоить значению переменной p значение первого, не зачеркнутого числа записанной последовательности, которое большее p;
- повторять 3-й и 4-й, пока возможно.
Если все сделано правильно, то в списке останутся не зачеркнутыми все простые числа от двух до n.
Для реализации решета Эратосфена на электронно-вычислительной машине используют модернизированный алгоритм. На 3-м шаге можно зачеркивать числа, начиная с числа p2, так как все составные числа, которые меньше него, к этому времени уже будут зачеркнуты. Тогда остановка работы алгоритма должна произойти, когда выполнится условие p2>n.
Следует также учесть, что все простые числа, за исключением двойки, — нечетные, поэтому, начиная с p2 можно «фильтровать» по 2p.

Видео по теме
Основная теорема арифметики
Согласно определению, простое число имеет два делителя. Один из них — 1, а второй — сама эта величина.
Прежде чем выяснить, каково число простых делителей числа, стоит уделить немного времени изучению основной теоремы арифметики. Согласно ей, натуральное число n > 1 можно представить, как n = p1*… ⋅*pk, где p1, … , pm — простые числа. При этом такое представление является единственным с точностью до порядка следования его сомножителей.
Следствие этой теоремы можно сформулировать следующим образом: любое натуральное число n представимо в виде n = p1d1*p2d2 * …* pkdm (в другой формулировке: каноническое разложение числа n на простые сомножители имеет вид n = p1d1*p2d2*⋅ …⋅*pkdm), где p1<p2< … <pm — простые числа, и d1, … , dm— некоторые натуральные числа.
Кроме того, уже известную вам основную теорему арифметики можно перефразировать следующим образом: любое каноническое разложение n можно считать тождественным, если не обращать внимания на порядок делителей. Это значит, что на практике для значительной части чисел существует множество достаточно простых алгоритмов их разложения на простые множители, которые в итоге дают один и тот же результат.
Критерий простоты
Прежде чем выяснить, как можно найти наибольший простой делитель числа (НПД) n, следует разобраться с другим важным вопросом.
Итак, выясним, по какому алгоритму можно установить, есть ли у величины другие делители кроме единицы и его самого.
Сделать это можно путем перебора простых чисел p1, …pk. Причем завершить цикл можно, как только pi+1, для которого производилась проверка, будет удовлетворять условию (pi+1)2> n.
Дадим объяснение, почему перебор можно ограничить pi>=sqr(n).
Предположим, у числа n, исследуемого на простоту есть некоторый делитель p. Тогда d=n/p так же будет его делителем. Но, так как d и p — разные числа, ни один из них не может быть больше корня из n.

Как найти наибольший простой делитель числа n
Найти НПД n, можно, действуя по следующей схеме:
- Разделить n на два, если оно четное или на три, если нечетное. Исключение составляет n, последняя цифра в десятичной записи которого ноль или пять. Такое число можно сразу разделить на пять.
- Если результат не целое число, то делят n на следующие целые числа, перебирая их вплоть до pi>=sqr(n).
Над получившимся числом n1 производят все действия, в том же порядке, что представлен выше, только с условием pi>=sqr(n1).
Если же ни на одном из шагов перебора n1 не делится на одно из простых чисел, то n целое и является своим же НПД. В противном случае получаем n2 и продолжаем деление с перебором до момента, когда на (i+1) шаге установим, что ni — целое.
Пример
Найдем простые делители числа 276.
- делим на "два";
- получаем 138;
- так как число четное, то вновь делим на "два";
- результат — 69;
- делим на следующее простое число "три";
- получаем 23.
Так как это число простое, можем подвести итог. Простыми делителями 276 являются 2, 3 и 23.
Как найти число простых делителей числа
Если речь идет о целом малом числе, то решение такой задачи не представляет никакой сложности. Рассмотрим конкретный пример. Найдем простые делители числа 54.
Для этого:
- 54 делим на "два" и получаем 27;
- 27 нечетное, поэтому разделим его уже не на "два", а на следующее простое число, т. е. "три";
- заметим, что 27=33;
- таким образом, разложение 54 имеет вид 54 = 21 * 33, т.е. простые делители числа 54 — это "два" и "три".
Однако это не все, что мы хотели знать. Теперь найдем число простых делителей числа 54. Оно равно произведению степеней простых множителей канонического разложения числа n = p1*d1 p2d2*⋅ …⋅*pmdm, увеличенных на 1. Иными словами, в общем случае K = (d1+1)*...* (dm+1).
Тогда для 54 имеем К = 2 * 4 = 8, т. е. общее число делителей равно восьми.
Обратите внимание, что все значительно упростилось, если бы речь шла о 23, 37, 103 и пр., так как каждый знает, сколько делителей у простого числа.

Пример
Найти число простых делителей числа 9990.
- так как число 9990 заканчивается на цифру "ноль", то оно делится на пять и на два.
- имеем 999.
- в результате деления на три имеем 333;
- снова делим на три, получаем 111;
- делим на три, имеем 37;
- 37 простое число, так как не делится без остатка ни на одно из простых чисел, которые находятся между двойкой и корнем из числа 37;
- подсчитываем количество простых делителей числа 9990. Это 2,3,5 и 37, то есть всего их четыре.
Проблема больших чисел
Как не странно, задача нахождения всех простых множителей числа является достаточно сложной. Дело в том, что до сих пор мы рассматривали только числа, десятичная запись которых состояла из одного-четырех знаков. Для них все вычисления выполняются в несколько шагов и их вполне можно осилить, имея под рукой лишь ручку и лист бумаги. По-другому обстоит дело, когда речь идет о, например, 1000-значном числе. Чтобы найти все его простые множители потребуется больше миллиарда лет, если даже будет задействован самый мощный суперкомпьютер в мире.
Простые числа и защита информации
Каждый современный человек, который пользуется возможностями, которые возникли благодаря появлению локальных компьютерных сетей и Интернета, нуждается в защите конфиденциальности своих личных данных, электронной переписки и пр. С этой целью используются криптографические алгоритмы с открытым ключом.
В системах с десятками и сотнями пользователей управление ключами является серьезной проблемой. Чтобы предотвратить овладение злоумышленником ключевой информацией, необходимо введение в процесс шифрования некой случайной величины.
Для этой цели наиболее распространенные на данный момент алгоритмы RSA используют большие простые числа.
Существует всего 10151 простых чисел длиною 1 - 512 битов включительно. В то же время для чисел, которые близки к n, вероятность того факта, что случайно выбранное число будет простым, — 1/ln n. Таким образом, полное количество простых чисел, которые меньше n равно n/ln n. Это позволяет считать, что крайне маловероятно, что 2 человека выберут одно и то же большое простое число.

Тест Миллера — Рабина
В криптографических целях часто используют именно этот вид определения простоты числа, который имеет несколько модификаций.
Тест Миллера—Рабина основан на проверке ряда условий, выполняемых для чисел, которые делятся только на 1 и на самих себя. Если хотя бы одно из требований нарушено, это «экзаменуемое» число признается составным.
Для данного m находятся целые нечетное число t и s, такие чтобы выполнялось условие m-1=2st.
Затем выбирается случайное число a, такое что 1<a<m. Если a не свидетельствует о простоте числа m, то программа должна выдать ответ «m составное» и завершить свою работу. В противном случае выбирается другое случайное число a и проверка повторяется снова. После того как будут установлены r свидетелей простоты, должен быть выдан ответ «m, вероятно, простое», и алгоритм завершит свою работу.
Следствием теоремы Рабина является тот факт, что если r чисел, которые выбраны случайно, признаны свидетелями для определения простоты числа m, то вероятность того, что оно составное, не может превосходить (4-r).

Теперь вы знаете, сколько делителей имеет простое число и как выяснить наиболее примитивный алгоритм вычисления НПД. Эти знания помогут вам в решении многих практических задач.
Источник: fb.ruКомментарии
 Идёт загрузка...
Идёт загрузка... Похожие материалы
 Еда и напитки Аристократичный мартини. Сколько градусов имеет любимый напиток?
Еда и напитки Аристократичный мартини. Сколько градусов имеет любимый напиток?Нет людей, равнодушных к этому напитку, особенно женщин. Это незыблемый символ роскошной и сладкой жизни. Конечно же, речь идет о мартини. Сколько градусов имеет он, какова история его возникновения, как пра...
 Путешествия Сколько провинций имеет Испания? Провинции Испании и их столицы
Путешествия Сколько провинций имеет Испания? Провинции Испании и их столицыВот уже сотни лет важнейшую роль на мировой арене играет Испания. Открытие Америки и инквизиция, коррида и фламенко, Гойя и Пикассо – это лишь малая часть ее славного прошлого и настоящего. К любопытным особенно...
 Образование Делители и кратные числа
Образование Делители и кратные числаТема «Кратные числа» изучается в 5 классе общеобразовательной школы. Ее целью является совершенствование письменных и устных навыков математических вычислений. На этом уроке вводятся новые понятия - «...
 Образование Простые числа: обыденность неразгаданной загадки
Образование Простые числа: обыденность неразгаданной загадкиПростые числа представляют собой одно из самых интересных математических явлений, которое привлекает к себе внимание ученых и простых граждан на протяжении уже более двух тысячелетий. Несмотря на то, что сейчас мы жив...
 Образование Взаимно простые числа. Основы
Образование Взаимно простые числа. ОсновыУчебники математики порой сложны для восприятия. Сухой и четкий язык авторов не всегда доступен для понимания. Да и темы там всегда взаимосвязанные, взаимовытекающие. Для освоения одной темы приходится поднимать ряд п...
 Духовное развитие Каждое слово имеет значение. Имя Назар: служитель Бога или просто "взгляд"?
Духовное развитие Каждое слово имеет значение. Имя Назар: служитель Бога или просто "взгляд"?Что означает имя Назар? Как ни странно, но единого толкования нет до сих пор. Одни счита...
 Еда и напитки Простой ответ на вопрос о том, сколько грамм сахара в столовой ложке
Еда и напитки Простой ответ на вопрос о том, сколько грамм сахара в столовой ложкеЕсли вы много времени проводите на кухне за созданием различных кулин...
 Еда и напитки Простой ответ на хороший вопрос – сколько сахара в столовой ложке?
Еда и напитки Простой ответ на хороший вопрос – сколько сахара в столовой ложке?В процессе приготовления новых блюд каждая хозяйка сталкивалась с трудностью измерения количества тех или иных продуктов. Зачастую в рецептах дают лишь общую информацию по закладке ингредиентов, опуская точные измерен...
 Еда и напитки Сколько нужно варить яйца: полезные факты о простом блюде
Еда и напитки Сколько нужно варить яйца: полезные факты о простом блюдеКазалось бы, что может быть проще, чем приготовить вареные яйца? Простое, даже элементарное блюдо, не требующее никаких особых познаний в кулинарии. Но как показывает практика, вопрос о том, сколько нужно варить яйца,...
 Еда и напитки Простые рецепты: сколько варить свинину
Еда и напитки Простые рецепты: сколько варить свининуСвинина является мясом, которое содержит большое количество жиров и иных питательных веществ, необходимых организму человека. Мясо свиньи достаточно легко готовится, из него делают супы, борщи, котлеты, рагу и запекан...
monateka.com
Наибольший общий делитель (НОД): определение, как найти, схема
Решим задачу. У нас есть два типа печенья. Одни шоколадные, а другие простые. Шоколадных 48 штук, а простых 36. Необходимо составить из этого печенья максимально возможное число подарков, при этом надо использовать их все.
Для начала выпишем все делители каждого из этих двух чисел, так как оба эти числа должны делиться на количество подарков.
Получаем,
- 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
- 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Найдем среди делителей общие, которые есть как у первого, так и у второго числа.
Общими делителями будут: 1, 2, 3, 4, 6, 12.
Наибольшим из всех общих делителей является число 12. Это число называют наибольшим общим делителем чисел 36 и 48.
Исходя из полученного результата, можем заключить, что из всего печенья можно составить 12 подарков. В одном таком подарке будет 4 шоколадных печенья и 3 обычных печенья.
Определение наибольшего общего делителя
- Наибольшее натуральное число, на которое делятся без остатка два числа a и b, называют наибольшим общим делителем этих чисел.
Иногда для сокращения записи используют аббревиатуру НОД.
Некоторые пары чисел имеют в качестве наибольшего общего делителя единицу. Такие числа называют взаимно простыми числами. Например, числа 24 и 35. Имеют НОД =1.
Как найти наибольший общий делитель
Для того чтобы найти наибольший общий делитель не обязательно выписывать все делители данных чисел.
Можно поступить иначе. Сначала разложить на простые множители оба числа.
- 48 = 2*2*2*2*3,
- 36 = 2*2*3*3.
Теперь из множителей, которые входят в разложение первого числа, вычеркнем все те, которые не входят в разложение второго числа. В нашем случае это две двойки.
- 48 = 2*2*2*2*3,
- 36 = 2*2*3*3.
Останутся множители 2, 2 и 3. Их произведение равно 12. Это число и будет являться наибольшим общим делителем чисел 48 и 36.
Это правило можно распространить на случай с тремя, четырьмя и т.д. числами.
Общая схема нахождения наибольшего общего делителя
- 1. Разложить числа на простые множители.
- 2. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.
- 3. Посчитать произведение оставшихся множителей.
Нужна помощь в учебе?
Предыдущая тема: Простые и составные числа: разложение чисел на простые множители Следующая тема:   Наименьшее общее кратное (НОК): определение, как найти, общая схемаВсе неприличные комментарии будут удаляться.
www.nado5.ru













