Аналитическая геометрия f(x)dx.Ru. Как построить график гиперболы функции
Математическая гипербола. Как построить гиперболу?
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Математическая гипербола.
Функция заданная формулой \(y=\frac{k}{x}\), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.Определение гиперболы.График функции \(y=\frac{k}{x}\) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.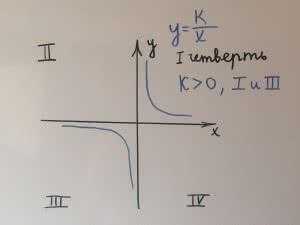
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти
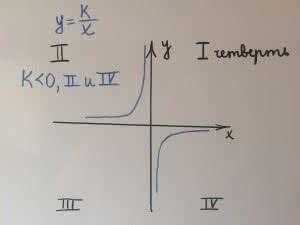гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти
Пример №2:$$y=\frac{1}{x+2}-1$$Находим первую асимптоту.Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.х+2≠0 х≠-2 это первая асимптота
Находим вторую асимптоту.
$$y=\color{red} {\frac{1}{x+2}}-1$$
Дробь \(\color{red} {\frac{1}{x+2}}\) отбрасываемОстается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Пример №3:
$$\begin{align*}&y=\frac{2+x}{1+x} \\\\&y=\frac{\color{red} {1+1}+x}{1+x} \\\\&y=\frac{1}{1+x}+\frac{1+x}{1+x}\\\\&y=\frac{1}{1+x}+1\\\\&y=\frac{1}{\color{red} {1+x}}+1\end{align*}$$
Находим первую асимптоту.Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.1+х≠0 х≠-1 это первая асимптота.
Находим вторую асимптоту.
$$y=\color{red}{\frac{1}{1+x}}+1$$
\(\color{red}{\frac{1}{1+x}}\) Дробь убираем.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
$$y=\frac{1}{x}$$
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.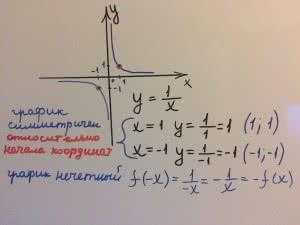
$$y=\frac{1}{x}$$
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
$$f(-x)=\frac{1}{-x}=-\frac{1}{x}=-f(x)$$
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
$$y=\frac{-1}{x-1}-1$$
а) Находим первую асимптоту.Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.x-1≠0 х≠1 это первая асимптота.
Находим вторую асимптоту.
$$y=\color{red} {\frac{-1}{x-1}}-1$$
Дробь \(\color{red} {\frac{-1}{x-1}}\) удаляем.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.х=0 y=0x=-1 y=-0,5x=2 y=-2x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находитсях ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находитсяy ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).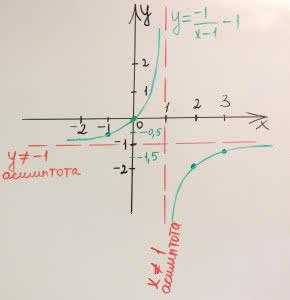
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.
8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.реклама
tutomath.ru
Построение гиперболы, с примерами
Схема построения графика гиперболы
Функцию, которую можно задать формулой вида называют обратной пропорциональностью. Кривая, которая является графиком функции , называется гиперболой.
Гипербола состоит из двух частей – веток гиперболы. Если , то ветви гиперболы расположены в I и III координатных четвертях, а если – то в II и IV четвертях.
Областью определения и областью значений функции , где , есть все числа, кроме 0. Гипербола не имеет общих точек с осью ординат.
Функция – нечетная функция, поскольку
значит, график функции симметричен относительно начала координат.
Если , то функция убывает на промежутке .
Если , то функция возрастает на промежутке .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Как построить гиперболу
В элементарной и высшей математике встречается такой термин, как гипербола. Так называют график функции, который не проходит через начало координат и представляет собой две параллельные друг другу кривые. Существует несколько способов построения гиперболы.
Инструкция
1
Гипербола так же, как и другие кривые может быть построена двумя способами. Первый из них заключается в построении по прямоугольнику, а второй - по графику функции f(x)=k/x.
Начинать строить гиперболу следует с построения прямоугольника с концами по оси x, именуемыми A1 и A2, и с противоположными концами по оси y, именуемыми B1 и B2. Проведите прямоугольник через центр координат, как показано на рисунке 1. Стороны должны быть параллельны и равны по величине как A1A2, так и B1B2. Через центр прямоугольника, т.е. начало координат, проведите две диагонали. Прочертив эти диагонали, вы получите две прямые, являющиеся асимптотами графика. Постройте одну ветвь гиперболы, а затем, аналогичным образом, и противоположную. Функция является возрастающей на промежутке [a;?]. Поэтому ее асимптотами будут: y=bx/a; y=-bx/a. Уравнение гиперболы примет вид:
y =b/a v x^2 -a^2
2
Если вместо прямоугольника использовать квадрат, получится равнобочная гипербола, как на рисунке 2. Ее каноническое уравнение имеет вид:
x^2-y^2=a^2
У равнобочной гиперболы асимптоты перпендикулярны друг другу. Кроме того, между y и x имеется пропорциональная зависимость, заключающаяся в том, что если x уменьшить в заданное число раз, то y увеличится во столько же раз, и наоборот. Поэтому, по-другому уравнение гиперболы записывается в виде:
y=k/x
3
Если в условии дана функция f(x)=k/x, то целесообразнее строить гиперболу по точкам. Учитывая, что k - величина постоянная, а знаменатель x?0, можно придти к выводу, что график функции не проходит через начало координат. Соответственно, интервалы функции равны (-?;0) и (0;?), так как при обращении x в ноль функция теряет смысл. При увеличении x функция f(x) убывает, а при уменьшении возрастает. При приближении x к нулю соблюдается условие y>?. График функции показан на основном рисунке.
4
Для построения гиперболы методом расчета удобно использовать калькулятор. Если он способен работать по программе или хотя бы запоминать формулы, можно заставить его осуществить расчет несколько раз (по числу точек), не набирая выражение каждый раз заново. Еще удобнее в этом смысле графический калькулятор, который возьмет на себя, помимо расчета, и построение графика.
Как простоmasterotvetov.com
Построение гиперболы. Эксцентриситет гиперболы. Равнобочная гипербола. » Аналитическая геометрия f(x)dx.Ru
п.5. Построение гиперболы.
Строим основной прямоугольник гиперболы и проводим его диагонали. Продолжая диагонали прямоугольника за его пределы, получаем асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции
.
Учитывая, что данная функция является возрастающей на промежутке , при и ее график приближается снизу к асимптоте , получаем:
рис.6.
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Осталось отобразить построенную правую ветвь гиперболы отобразить относительно оси Оу.
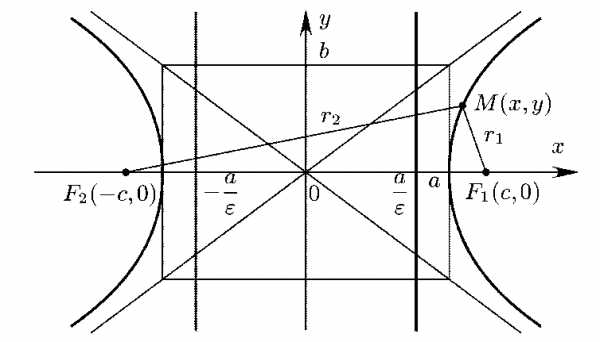
п.6. Эксцентриситет гиперболы.
По определению эксцентриситет гиперболы равен
. Зафиксируем действительную ось 2а и начнем изменять фокучное расстояние 2с. Так как , то при этом изменяется и величина b.
1) Пусть . При этом , и мнимые вершины стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы вырождается в пределе в отрезок , а сама гипербола вырождается в два луча на оси абсцисс: и .
2) Пусть . При этом , и мнимые вершины стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаеются к прямым и в пределе сливаются с ними. Гипербола вырождается в две прямые , параллельные оси Оу.
п.7. Равнобочная гипербола.
Определение. Равнобочной гиперболой называется гипербола, экчцентриситет которой равен .
Из определения следует, что в равнобочной гиперболе и ее каноническое уравнение имеет вид
.
Действительно, , откуда и . Учитывая, что а и b положительные числа, получаем .
Основной прямоугольник равнобочной гиперболы является квадратом, уравнения асимптот . Значит, асимптотами равнобочной гиперболы являются биссектрисы координатных углов, угол между которыми является прямым.
Введем новую ПДСК со старым началом координат, оси которой совпадают с асимптотами равнобочной гиперболы. Новую систему координат можно получить их старой, если одновременно повернуть старые оси координат вокруг начала координат по часовой стрелки на угол .
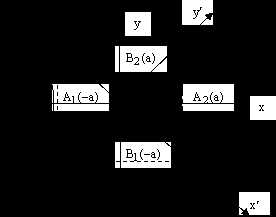
рис.7.
Без доказательства примем следующую теорему.
Теорема. В новой системе координат уравнение равнобочной гиперболы имеет вид
,
где .
Из теоремы следует, что если уравнение равнобочной гиперболы в новой системе координат имеет вид
, то в старой канонической системе координат ее уравнение имеет вид , т.е. .
Возможно найдутся ответы здесь:
fxdx.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике - Алгебра
Гипербола на координатной плоскости
Определение 1. Гиперболой (равносторонней гиперболой) называют график функции
| (1) |
где k – любое, отличное от нуля, число.
Функция (1) обладает следующими свойствами:
Рассмотрим теперь функцию, заданную формулой
| (2) |
где a, b, c, d – произвольные числа, а число c не равно нулю.
Определение 2. Дробно-линейной функцией называют функцию, заданную формулой (2), если дробь, стоящая в правой части формулы (2), несократима.
Графиком дробно–линейной функции является гипербола.
Примеры графиков дробно–линейных функций
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Гиперболические графики функций, общий вид гиперболической функции
Функция записывается в общем виде, как y = или f(x) =
y и x - это обратно пропорциональные величины, т.е. когда одна растет, другая уменьшается (проверьте, подставив числа в функцию)
В отличие от предыдущей функции, в которой x2 всегда создает положительные значения, здесь мы не можем сказать, что - = , поскольку это будут совершенно противоположные числа. Такие функции называют нечетными.
Построим для примера график y =
Естественно, x не может быть равен нулю (x ≠ 0)
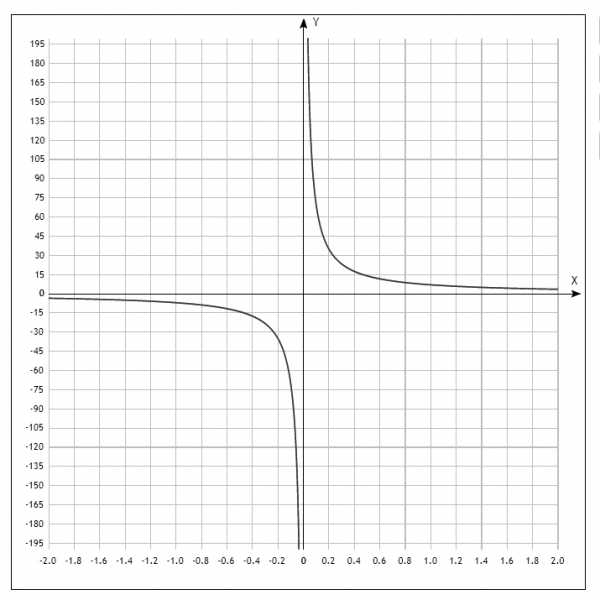Ветви гиперболы лежат в 1-й и 3-й части координат.
Они бесконечно могут приближаться к осям абсцисс и ординат и так никогда их не достигнуть, даже если «x» станет равен миллиарду. Гипербола будет бесконечно близко, но все же так и не пересечется с осями (такая вот математическая печалька).
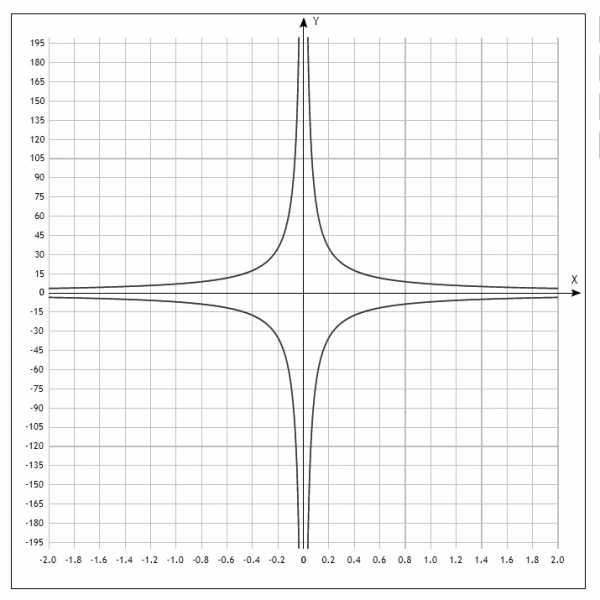
Построим график для y = -
И теперь ветви гиперболы находятся во второй и 4-й четверти частях координатной плоскости.
В итоге, между всеми ветвями можно наблюдать полную симметрию.
Далее, подобным образом, вы сможете строить любые другие графики, опираясь на эти.
Добавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
uchilegko.info
Содержание
Инструкция
|
completerepair.ru
