ГлавнаяРазноеКак правильно делить дроби десятичные дроби

Деление десятичных дробей объяснение и примеры. Как правильно делить дроби десятичные дроби


Как делить десятичные дроби?

Если ваш ребенок никак не может усвоить, как делить десятичные дроби, то это не повод считать его не способным к математике.

Скорее всего, ему просто непонятно объяснили, как это делается. Нужно помочь ребенку и в максимально простой, почти игровой, форме рассказать ему о дробях и операциях с ними. А для этого надо и самим кое-что вспомнить.

Что такое дроби

Дробные выражения применяются когда речь идет о числах нецелых. Если дробь меньше единицы, значит, она описывает часть чего-то, если больше — несколько целых частей и еще кусочек. Дроби описываются 2 значениями: знаменателем, объясняющим, на сколько равных частей поделено число и числителем, который говорит о том, сколько таких частей мы имеем в виду.

Допустим, вы разрезали пирог на 4 равных части и 1 из них отдали соседям. Знаменатель будет равен 4. А числитель зависит от того, что мы хотим описать. Если мы рассказываем о том, сколько было отдано соседям, то числитель равен 1, а если речь идет о том, сколько осталось, то 3.

В примере с пирогом знаменатель — 4, а в выражении «1 день — 1/7 недели» — 7. Дробное выражение с любым знаменателем представляет собой обыкновенную дробь.

Математики, как и все, стараются облегчить себе жизнь. И поэтому были придуманы дроби десятичные. В них знаменатель равен 10 или числам, кратным 10 (100, 1000, 10 000 и т.д.), а записывают их следующим образом: целая составляющая числа отделяется от дробной с помощью запятой. Например, 5,1 — это 5 целых и 1 десятая, а 7,86 — это 7 целых и 86 сотых.

Небольшое отступление — не для ваших детей, а для вас самих. Отделять дробную часть запятой принято именно в нашей стране. За рубежом по устоявшейся традиции принято отделять ее с помощью точки. Поэтому, если встретите в иностранном тексте подобную разметку — не удивляйтесь.

Деление дробей

Каждое арифметическое действие с подобными числами имеет свои особенности, но сейчас мы попытаемся усвоить как делить десятичные дроби. Возможно деление дроби на натуральное число или на другую дробь.

Для того, чтобы было проще осваивать эту арифметическую операцию, важно запомнить одну простую вещь.

Научившись управляться с запятой, можно использовать те же правила деления, что и для целых чисел.

Рассмотрим деление дроби на натуральное число. Технология деления в столбик, должна быть вам уже известна из ранее пройденного материала. Процедура проводится аналогично. Делимое познаково делится на делитель. Как только очередь дойдет до последнего перед запятой знака, запятая ставится и в частном, а далее деление проходит в обычном порядке.

То есть, не считая сноса запятой — самое обычное деление, да и запятая большой сложности не представляет.

Деление дроби на дробь

Примеры, к которых нужно делить одно дробное значение на другое, кажутся на вид очень сложными. Но на самом деле, с ними ничуть не труднее управиться. Одну десятичную дробь поделить на другую будет намного легче, если избавиться от запятой в делителе.

Как это сделать? Если вам надо разложить 90 карандашей по 10 коробкам, то сколько карандашей будет в каждой из них? 9. Давайте умножим оба числа на 10 — 900 карандашей и 100 коробок. Сколько в каждой? 9. Тот же принцип применяется и в случае, когда нужно поделить десятичную дробь.

Делитель избавляется от запятой вообще, а у делимого запятая переносится вправо на столько знаков, сколько их было ранее в делителе. А далее проводится обычное деление в столбик, которое мы рассмотрели выше. Например:

25,6/6,4 = 256/64 = 4;

10,24/1,6 = 102,4/16 =6,4;

100,725/1,25 =10072,5/125 =80,58.

Делимое нужно умножать и умножать на 10 до тех пор, пока делитель не превратится в целое число. Поэтому у него могут появиться дополнительные нули справа.

40,6/0,58 =4060/58=70.

Ничего страшного в этом нет. Вспомните пример с карандашами — ответ не изменится, если вы увеличите оба числа в одинаковое количество раз. Обыкновенную дробь поделить сложнее, особенно при отсутствии общих множителей в числителе и знаменателе.

Делить десятичную в этом плане гораздо удобнее. Самым сложным здесь является трюк с переносом запятой, но как мы с вами увидели, с ним легко справиться. Сумев донести это до своего ребенка, вы тем самым научите его делить десятичные дроби.

Овладев этим нехитрым правилом, ваш сын или ваша дочь будет гораздо уверенней чувствовать себя на уроках математики и, как знать, может быть, увлечется этим предметом. Математический склад ума редко проявляется с раннего детства, иногда нужен толчок, заинтересованность.

Помогая своему ребенку с выполнением уроков, вы не только улучшите успеваемость, но и расширяете круг его интересов, за что со временем он вам будет благодарен.

lediznaet.ru

Деление десятичных дробей объяснение и примеры - Арифметика

При делении десятичных дробей вам могут встретиться несколько случаев.

Деление десятичной дроби на натуральное число

Для деления десятичной дроби на натуральное число пользуемся следующими правилами.

  1. Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
  2. Ставим в частном запятую, когда заканчивается деление целой части делимого.

Если целая часть делимого меньше делителя, то в частном ставим 0 целых.

Пример:

0,806 : 31 = 

Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31). Поэтому в частном сразу ставим 0 в целой части.

Не забываем записывать ответ в пример:

0,806 : 31 = 0,026 

Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.

Примеры:

Деление натурального числа на десятичную дробь

  1. Считаем количество знаков справа от запятой в десятичной дроби.
  2. Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., чтобы превратить десятичную дробь в целое число.
  3. Делим числа как натуральные.

Пример:

5 : 2,5 =

Считаем количество знако после запятой в десятичной дроби. У нас один знак. Значит, чтобы превратить 2,5 в целое число, надо умножить его на 10. Не забываем и делимое умножить на 10.

5 : 2,5 = (5 • 10) : (2,5 • 10) = 50 : 25 = 2

 

Деление десятичных дробей друг на друга

Делить десятичные дроби друг на друга можно разными способами. Мы опишем один из возможных. По традиции, небольшой план действий:

  1. Определяем дробь с наибольшим количеством знаков (цифр) справа от запятой.

  2. Умножаем обе десятичные дроби на 10, 100, 1000 и т.д., чтобы превратить десятичные дроби в целые числа.

  3. Делим обыкновенные числа по правилам деления в столбик и записываем ответ.

Пример:

 7,1 : 0,1 = 7,1 • 10 = 71

intellect.ml

Деление дробей. Правила. Примеры. | tutomath

Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.

Деление дроби на дробь.

Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.

\(\bf \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}\\\)

Пример:

Выполните деление обыкновенных дробей  .

Деление дроби на число.

Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.

\(\bf \frac{a}{b} \div n = \frac{a}{b} \div \frac{n}{1} = \frac{a}{b} \times \frac{1}{n}\\\)

Рассмотрим пример:

Выполните деления дроби на натуральное число \(\frac{4}{7} \div 3\).

Как мы уже знаем, что любое число можно представить в виде дроби \(3 = \frac{3}{1} \).

\(\frac{4}{7} \div 3 = \frac{4}{7} \div \frac{3}{1} = \frac{4}{7} \times \frac{1}{3} = \frac{4 \times 1}{7 \times 3} = \frac{4}{21}\\\)

Деление числа на дробь.

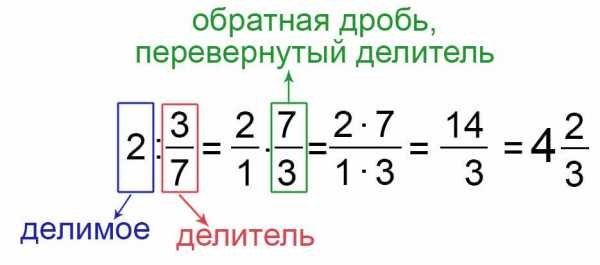
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.

Рассмотрим пример:

Выполните деление числа на дробь.

Деление смешанных дробей.

Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.

Пример:

Выполните деление смешанных дробей.

\(2\frac{3}{4} \div 3\frac{1}{6} = \frac{11}{4} \div \color{red} {\frac{19}{6}} = \frac{11}{4} \times \color{red} {\frac{6}{19}} = \frac{11 \times 6}{4 \times 19} = \frac{11 \times \color{red} {2} \times 3}{2 \times \color{red} {2} \times 19} = \frac{33}{38}\\\)

Деление числа на число.

Чтобы поделить простые числа, нужно представить их в виде дроби  и выполнить деление по правилам деления дроби на дробь.

Пример:

\(2 \div 5 = \frac{2}{1} \div \color{red} {\frac{5}{1}} = \frac{2}{1} \times \color{red} {\frac{1}{5}} = \frac{2 \times 1}{1 \times 5} = \frac{2}{5}\\\)

Примечание к теме деление дробей:На нуль делить нельзя.

Вопросы по теме:Как делить дроби? Как разделить дробь на дробь?Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.

Как делить дроби с разными знаменателями?Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.

Пример №1:Выполните деление и назовите делитель, дробь, обратную делителю: а) \(\frac{5}{9} \div \frac{8}{13}\) б) \(2\frac{4}{5} \div 1\frac{7}{8}\)

Решение:а) \(\frac{5}{9} \div \frac{8}{13} = \frac{5}{9} \times \frac{13}{8} = \frac{65}{72}\\\\\)

\( \frac{8}{13}\) – делитель, \( \frac{13}{8}\) – обратная дробь делителя.

б) \(2\frac{4}{5} \div 1\frac{7}{8} = \frac{14}{5} \div \frac{15}{8} = \frac{14}{5} \times \frac{8}{15} = \frac{14 \times 8}{5 \times 15} = \frac{112}{75} = 1\frac{37}{75}\\\\\)

\( \frac{15}{8}\) – делитель, \( \frac{8}{15}\) – обратная дробь делителя.

Пример №2:Вычислите деление: а) \(5 \div 1\frac{1}{4}\) б) \(9\frac{2}{3} \div 8\)

Решение:

а) \(5 \div 1\frac{1}{4} = \frac{5}{1} \div \frac{5}{4} = \frac{5}{1} \times \frac{4}{5} = \frac{\color{red} {5} \times 4}{1 \times \color{red} {5}} = \frac{4}{1} = 4 \\\\\)

б) \(9\frac{2}{3} \div 8 = \frac{29}{3} \div \frac{8}{1} = \frac{29}{3} \times \frac{1}{8} = \frac{29 \times 1}{3 \times 8} = \frac{29}{24} = 1\frac{5}{24}\\\\\)

tutomath.ru

Как делить десятичные дроби

При делении двух десятичных дробей, когда под рукой не оказывается калькулятора, многие испытывают некоторые затруднения. На самом деле тут нет ничего сложного. Десятичные дроби называются таковыми, если в их знаменателе число, кратное 10. Как правило, такие числа записываются в одну строчку и имеют запятую, отделяющую дробную часть от целой. Видимо по причине наличия дробной части, которая к тому же отличается количеством знаков после запятой, многим не понятно, как производить без калькулятора математические действия с такими числами.

Вам понадобится

лист бумаги, карандаш

Спонсор размещения P&G Статьи по теме "Как делить десятичные дроби" Как решать уравнения с дробями Как перевести в десятичную дробь Как решать дроби 5 класса

Инструкция

1

Итак, для того, чтобы разделить одну десятичную дробь на другую, нужно посмотреть на оба числа и определить, у какого из них больше знаков после запятой. Умножаем оба числа на число, кратное 10, т.е. 10, 1000 или 100000, количество нулей в котором равно большему количеству знаков после запятой одного из двух наших исходных чисел. Теперь обе десятичные дроби превратились в обыкновенные целые числа. Берем лист бумаги с карандашом и делим два получившихся числа "уголком". Получаем результат.

2

Например, нам нужно разделить число 7,456 на 0,43. Первое число имеет больше знаков после запятой (3 знака), поэтому умножаем оба числа не 1000 и получаем два простых целых числа: 7456 и 430. Теперь делим "уголком" 7456 на 430 и получаем, что, если 7,456 разделить 0,43 выйдет примерно 17,3.

3

Существует еще один способ деления. Записываем десятичные дроби в виде простых дробей с числителем и знаменателем, для нашего случая это 7456/1000 и 43/100. После этого записываем выражение для деления двух простых дробей:7456*100/1000*43,затем сокращаем десятки, получаем:7456/10*43 = 7456/430В конечном итоге опять получаем деление двух простых чисел 7456 и 430, которое можно произвести "уголком".

Как просто

masterotvetov.com

Деление дробей | Математика

Деление дробей — тема, которая включает в себя действия с обыкновенными дробями, смешанными числами и десятичными дробями.

Запишем на одной странице все правила, касающиеся деления обыкновенных дробей, смешанных чисел и натуральных чисел.

1. Деление обыкновенных дробей.

Чтобы разделить дробь на дробь, надо делимое умножить на число, обратное делителю.

(то есть первую дробь нужно переписать без изменений и умножить её на «перевёрнутую» вторую дробь).

   

При умножении дробей проще сокращать множители, чем результат.

Если в результате получается неправильная дробь, нужно выделить из неё целую часть.

Примеры деления обыкновенных дробей:

   

   

   

2. Деление обыкновенной дроби на натуральное число.

Применив правило деления обыкновенных дробей

   

приходим к выводу:

Чтобы разделить дробь на натуральное число, надо знаменатель умножить на это число, а числитель оставить без изменения.

Примеры деления обыкновенной дроби на число:

   

   

   

Заметим, что если числитель дроби делится на число без остатка, при делении можно числитель разделить на число, а знаменатель оставить тем же:

   

   

Стоит ли запоминать ещё одно правило или использовать одно правило для всех случаев — решать вам.

3. Деление натурального числа на дробь.

Применив правило деления обыкновенных дробей

   

приходим к выводу:

чтобы разделить натуральное число на дробь, надо в числитель записать произведения этого числа и знаменателя, а в знаменатель записать числитель.

   

Можно запомнить это правило и применять его в дальнейшем. А можно делить число на дробь, применяя для всех случаев деления дробей одно правило. Выбирайте, что для вас удобнее.

Примеры деления натурального числа на дробь:

   

   

   

Здесь можно сделать ещё один вывод:

   

4. Деление смешанных чисел.

Чтобы разделить смешанные числа (смешанные дроби), надо превратить их в неправильные дроби и разделить по правилу деления обыкновенных дробей:

   

(эту формулу запоминать не надо. Достаточно знать, как  переводить смешанные дроби в неправильные и делить обыкновенные дроби).

Примеры деления смешанных дробей:

   

   

   

Примеры деления смешанного числа и обыкновенной дроби:

   

   

В следующий раз рассмотрим все правила, касающиеся деления десятичных дробей.

www.for6cl.uznateshe.ru

Как делить дроби?

Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.

Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:

  1. Верхняя часть дроби называется числителем, а нижняя – знаменателем.
  2. При делении числа называются так: делимое : делитель = частное

Как делить дроби: простые дроби

Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:

3/77 : 1/11 = 3 /77 * 11 /1 = 3/7

Как делить дроби: смешанные дроби

Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:

10 2/3 : 4/15 = 32/3 : 4/15 = 32/3 * 15 /4 = 40/1 = 40

Как делить дробь на число

Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:

5/11 : 7 = 5/11 : 7/1 = 5/11 * 1/7 = 5/77

Как делить десятичные дроби

Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.

Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно,

elhow.ru

Деление десятичных дробей - 5 класс - Математика - Каталог статей

Деление десятичных дробейПри делении десятичных дробей вам могут встретиться несколько случаев.Деление десятичной дроби на натуральное числоДля деления десятичной дроби на натуральное число пользуемся следующими правилами.1.    Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.2.    Ставим в частном запятую, когда заканчивается деление целой части делимого.    

Пример:

0,806 : 31 = 

Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31). Поэтому в частном сразу ставим 0 в целой части. Не забываем записывать ответ в пример:

0,806 : 31 = 0,026

Примеры:310,1 : 10 = 31,0127,56 : 100 = 0,27560,75 : 10 = 0,075Деление натурального числа на десятичную дробь1.    Считаем количество знаков справа от запятой в десятичной дроби.2.    Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., чтобы превратить десятичную дробь в целое число.3.    Делим числа как натуральные.Пример:

5 : 2,5 =

Считаем количество знаков после запятой в десятичной дроби. У нас один знак. Значит, чтобы превратить 2,5 в целое число, надо умножить его на 10. Не забываем и делимое умножить на 10.

5 : 2,5 = (5 • 10) : (2,5 • 10) = 50 : 25 = 2

Деление десятичных дробей друг на другаДелить десятичные дроби друг на друга можно разными способами. Мы опишем один из возможных. По традиции, небольшой план действий:1.    Определяем дробь с наибольшим количеством знаков (цифр) справа от запятой.2.    Умножаем обе десятичные дроби на 10, 100, 1000 и т.д., чтобы превратить десятичные дроби в целые числа.3.    Делим обыкновенные числа по правилам деления в столбик и записываем ответ.Пример: 7,44:0,4=•    Наибольшее количество знаков (цифр) после запятой у первой десятичной дроби, поэтому ориентируемся на неё. Чтобы превратить 7,44 в целое число нужно умножить его на 100.    

 (7,44*100):(0,4*100)=•    Умножаем каждую из десятичных дробей на 100. (7,44*100):(0,4*100)=744*40=•    Делим обыкновенные числа в столбик и записываем ответ. Помним, что изначально мы делили десятичные дроби.     

Примеры:7,1 : 0,1 = 7,1 • 10 = 71

25,37 : 0,001 = 25,37 • 1 000 = 25 3700,08 : 0,1 = 0,08 • 10 = 0,8

matematik.3dn.ru