ГлавнаяРазноеКак решить матрицы

Решение матриц. Объясняем, как решать матрицы. Как решить матрицы


Решение уравнений методом обратной матрицы

Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений.

Суть метода

Пусть задана система линейных уравнений с неизвестными:

   

Эту систему можно записать в виде матричного уравнения ,

где – матрица системы,

– столбец неизвестных,

– столбец свободных коэффициентов.

Из полученного матричного уравнения необходимо выразить . Для этого умножим обе части матричного уравнения слева на , получим:

   

Так как , то или .

Далее находится обратная матрица и умножается на столбец свободных членов .

ЗАМЕЧАНИЕ Обратная матрица к матрице существует только при условии, что . Поэтому при решении системы линейных уравнений методом обратной матрицы в первую очередь вычисляется . Если , то система имеет единственное решение, которое можно найти методом обратной матрицы, если же , то методом обратной матрицы решить эту систему нельзя.

Пример решения методом обратной матрицы

ПРИМЕР 1
Задание Решить систему линейных уравнений методом обратной матрицы

   

Решение Данная система уравнений может быть записана матричным уравнением

   

где , , .

Выразив из этого уравнения , получим

   

Найдем определитель матрицы :

   

   

Так как , то система имеет единственное решение, которое можно найти методом обратной матрицы.

Найдем обратную матрицу с помощью союзной матрицы. Вычислим алгебраические дополнения к соответствующим элементам матрицы :

   

   

   

   

   

Запишем союзную матрицу , составленную из алгебраических дополнений элементов матрицы :

   

Далее запишем обратную матрицу согласно формуле . Будем иметь:

   

Умножая обратную матрицу на столбец свободных членов , получим искомое решение исходной системы:

   

Ответ
Читайте также:

Умножение матрицы на вектор

Ранг матрицы

Вычитание матриц

Перемножение матриц

Элементарные преобразования матриц

Операции над матрицами и их свойства

ru.solverbook.com

Как решать матрицы?

Математическая матрица – это таблица упорядоченных элементов. Размеры этой таблицы определяются по количеству строк и столбцов в ней. Что касается решения матриц, то им называют огромное количество операций, которые производятся над этими самыми матрицами. Математики различают несколько видов матриц. Для некоторых из них действуют общие правила по решению, а для других не действуют. Например, если матрицы имеют одинаковую размерность, то их можно сложить, а если они согласовываются между собой, то их можно перемножить. Обязательно для решения любой матрицы необходимо найти детерминант. Кроме того, матрицы подвергаются транспонированию и нахождению в них миноров. Итак, давайте рассмотрим, как решать матрицы.

Порядок решения матриц

Сначала записываем заданные матрицы. Считаем сколько в них строк и столбцов. Если количество строк и столбцов одинаковое, то такая матрица называется квадратной. Если каждый элемент матрицы оказался равен нулю, то такая матрица нулевая. Следующее, что мы делаем, это находим главную диагональ матрицы. Элементы такой матрицы находятся от правого нижнего угла до левого верхнего. Вторая же диагональ в матрице является побочной. Теперь необходимо произвести транспонирование матрицы. Чтобы это сделать, необходимо заменить в каждой из двух матриц элементы строк на соответствующие элементы столбцов. Например, элемент под а21 окажется элементом а12 или же наоборот. Таким образом, после этой процедуры должна появиться совершенно иная матрица.

Если матрицы имеют совершенно одинаковую размерность, то их можно запросто сложить. Чтобы это сделать, мы берем первый элемент первой матрицы а11 и складываем его с подобным элементом второй матрица b11. То, что получится в результате, записываем на ту же позицию, только уже в новую матрицу. Теперь аналогичным образом складываем все остальные элементы матрицы, пока не получится новая совершенно иная матрица. Посмотрим еще несколько способов, как решать матрицы.

Варианты действий с матрицами

Также мы можем определить, являются ли согласов

elhow.ru

Матричный метод решения систем линейных уравнений

Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.

Другое условие применимости матричного метода - невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.

Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.

Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .

Пусть нужно решить систему линейных уравнений:

Запишем эту систему уравнений в матричном виде:

Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов

.

Тогда

То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.

Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.

Пример 1. Решить матричным методом систему линейных уравнений:

Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица неизвестных:

Матрица свободных членов:

Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:

По выведенному выше последнему равенству и будем вычислять решения данной системы.

Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:

.

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Сделаем проверку:

Следовательно, ответ правильный.

Для второго примера выберем систему линейных уравнений третьего порядка.

Пример 2. Решить матричным методом систему линейных уравнений:

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица неизвестных:

Матрица свободных членов:

Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:

.

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Сделаем проверку:

Следовательно, ответ правильный.

Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение

Всё по теме "Системы уравнений и неравенств"

Начало темы "Линейная алгебра"

Поделиться с друзьями

function-x.ru

Решение матриц онлайн

Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, при этом сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придет многофункциональный математический калькулятор. В его арсенал входит решение матриц онлайн, в нашем калькуляторе можно выполнить все основные операции над матрицами!

Матрица — это совокупность значений, записанных в прямоугольную таблицу. Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трех строк и пяти столбцов.

Обратите внимание, 5 x 5 — это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.

Как решать матрицы в онлайн калькуляторе?

Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.

Кнопка, открывающая калькулятор матриц:

Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн. Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.

Кнопки калькулятора, выполняющие основные действия над матрицами:

Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения. В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами.

Вычисление матриц онлайн с помощью формы быстрого ввода:

Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».

Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I», чтобы увидеть дисплей в полный размер.

Вектор столбец

Матрица, состоящая только из одной строки или одного столбца, называется вектор-строкой или вектор-столбцом соответственно. В калькуляторе предусмотрены отдельные кнопки для ввода матрицы, число столбцов которой равно 1. Используйте эти клавиши, чтобы записать вектор-столбец из 3, 4 или 5 строк соответственно.

Кнопки калькулятора для ввода вектора:

Вектор-столбец из 3-х строк:(2, 6, 8)

Квадратная матрица

Матрица называется квадратной, если число ее строк равно числу столбцов. Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы — линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.

Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки калькулятора.

Кнопки калькулятора для ввода квадратных матриц:

Пример квадратной матрицы 4 порядка:[[8, 4, 1, 8][7, 1, 8, 8][8, 4, 1, 6][4, 8, 3, 1]]

Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.

Пример симметричной матрицы:[[1, 2, 8, 11][2, 3, 24, 5][8, 24, 6, 4][11, 5, 4, 9]]

Есть еще такие виды матриц в математике.

Единичная матрица чисел — это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.

Пример единичной матрицы:[[1, 0, 0, 0][0, 1, 0, 0][0, 0, 1, 0][0, 0, 0, 1]]

Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.

Пример нулевой матрицы:[[0, 0, 0, 0][0, 0, 0, 0][0, 0, 0, 0][0, 0, 0, 0]]

Сложение и вычитание матриц онлайн

С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.

Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, то-есть число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.

Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.

Сложение матриц примеры

Сложение двух матриц:[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]

Сумма двух матриц:[[2, 7][4, 5]]+[[2, 10][6, 8]]

Векторное произведение матриц

Для выполнения этой операции используйте клавишу Cross Product.

Пример произведения векторов:(2, 6, 4)#(8, 2, 5)

Умножение матриц

Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.

Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.

Умножение матриц пример:[[2, 8][4, 2]]*[[8, 8][7, 1]]

Умножение матрицы на число онлайн:[[5, 6][7, 8]]*9

Решение матричных уравнений

Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой. Решение матричных уравнений осуществляется с помощью кнопки Solve Ecuation System.

Пример решения системы уравнений матриц:[[6, 1, 8],[7, 5, 3],[2, 9, 4]]*x=(1, 2, 3)

Транспонирование матрицы

Используйте клавишу Matrix Transponent, когда нужно выполнить транспонирование матрицы — действие, в котором строки со столбцами меняются местами. Таким образом, транспонированная матрица получается путем замены строк на столбы в исходной матрице.

Использовать калькулятор матриц, чтобы транспонировать матрицу онлайн, очень просто. Нужно заполнить данные исходной матрицы и нажать кнопку Matrix Transponent. Нахождение транспонированной матрицы ^Т также можно выбрать из выпадающего меню в поле выбора действия с матрицами.

Найти транспонированную матрицу можно у любой матрицы вне зависимости от количества ее строк и столбцов (не забывайте, калькулятор матриц имеет ограничение на размер матрицы — максимум 5 x 5).

Транспонирование матрицы онлайн калькулятором:[[2, 3, 4][1, 5, 8][7, 1, 4]]^T

Решение обратной матрицы

Обратной матрицей называют таблицу, при умножении на которую исходная матрица принимает вид единичной матрицы (применимо только к квадратным видам матриц).

Нахождение обратной матрицы осуществляется с помощью кнопки Matrix Inverse.

Пример нахождения обратной матрицы:[[2, 4][2, 2]]^-1

Нахождение определителя матрицы

В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию — оператор det(Determinant).

Пример, как найти определитель матрицы онлайн:det([[-2, 2, -3],[-1, 1, 3],[2, 0, -1]])

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Решение матриц онлайн was last modified: Март 3rd, 2016 by Admin

compuzilla.ru

Как найти решение матрицы

Математическая матрица является упорядоченной таблицей элементов с определенным числом строк и столбцов. Чтобы найти решение матрицы, необходимо определить, какое действие требуется над ней выполнить. После этого действуйте согласно имеющимся правилам работы с матрицами

Инструкция

completerepair.ru

Как решать матрицы

Математическая матрица представляет собой упорядоченную таблицу элементов. Размерность матрицы определяется числом ее строк m и столбцов n. Под решением матриц понимается множество обобщающих операций, производимых над матрицами. Различают несколько типов матриц, к некоторым из них не применим ряд операций. Существует операция сложения для матриц с одинаковой размерностью. Произведение двух матриц находится, только если они согласованны. Для любой матрицы определяется детерминант. Также матрицу можно транспонировать и определить минор ее элементов.

Спонсор размещения P&G Статьи по теме "Как решать матрицы" Как находить определитель матрицы Как вычислять определитель матрицы Как находить обратную матрицу

Инструкция

1

Запишите заданные матрицы. Определите их размерность. Для этого посчитайте количество столбцов n и строк m. Если для одной матрицы m = n, матрица считается квадратной. Если все элементы матрицы равны нулю – матрица нулевая. Определите главную диагональ матриц. Ее элементы располагаются с левого верхнего угла матрицы до правого нижнего. Вторая, обратная диагональ матрицы является побочной.

2

Проведите транспонирование матриц. Для этого замените в каждой матрице элементы строк на элементы столбцов относительно главной диагонали. Элемент а21 станет элементом а12 матрицы и наоборот. В итоге из каждой исходной матрицы получится новая транспонированная матрица.

3

Сложите заданные матрицы, если они имеют одинаковую размерность m х n. Для этого возьмите первый элемент матрицы а11 и сложите его с аналогичным элементом b11 второй матрицы. Результат сложения запишите в новую матрицу на ту же позицию. Затем сложите элементы а12 и b12 обоих матриц. Таким образом заполните все строки и столбцы суммирующей матрицы.

4

Определите, являются ли заданные матрицы согласованными. Для этого сравните число строк n в первой матрицы и число столбцов m второй матрицы. Если они равны, выполните произведение матриц. Для этого попарно умножьте каждый элемент строки первой матрицы на соответствующий элемент столбца второй матрицы. После чего найдите сумму этих произведений. Таким образом, первый элемент результирующей матрицы g11 = а11* b11 + а12*b21 + а13*b31 + … + а1m*bn1. Выполните умножение и сложение всех произведений и заполните результирующую матрицу G.

5

Найдите определитель или детерминант для каждой заданной матрицы. Для матриц второго порядка - размерностью 2 на 2 – определитель находится, как разница произведений элементов главной и побочной диагоналей матрицы. Для трехмерной матрицы формула определителя: D = а11* а22*а33 + а13* а21*а32 + а12* а23*а31 - а21* а12*а33 - а13* а22*а31 - а11* а32*а23.

6

Для нахождения минора определенного элемента вычеркните из матрицы строку и столбец, где расположен данный элемент. Затем определите детерминант полученной матрицы. Это и будет минор элемента.

Как просто

masterotvetov.com

Решение матриц. Объясняем, как решать матрицы.

Решение матриц – понятие обобщающее операции над матрицами. Под математической матрицей понимается таблица элементов. О подобной таблице, в которой m строк и n столбцов, говорят что это матрица размером m на n.Общий вид матрицы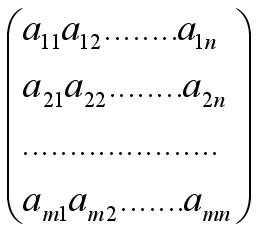Основные элементы матрицы:Главная диагональ. Её составляют элементы а11,а22…..аmn Побочная диагональ. Её слагают элементы а1n,а2n-1…..аm1 .Перед тем как перейти к решению матриц рассмотрим основные виды матриц:Квадратная – в которой число строк равно числу столбцов (m=n)Нулевая – все элементы этой матрицы равны 0.Транспонированная матрица — матрица В, полученная из исходной матрицы A заменой строк на столбцы.Единичная – все элементы главной диагонали равны 1, все остальные 0.Обратная матрица — матрица , при умножении на которую исходная матрица даёт в результате единичную матрицу.Матрица может быть симметричной относительно главной и побочной диагонали. То есть, если а12=а21 , а13=а31,….а23=а32…. аm-1n=аmn-1. то матрица симметрична относительно главной диагонали. Симметричными бывают только квадратные матрицы.Теперь перейдем непосредственно к вопросу, как решать матрицы.

Сложение матриц.

Матрицы можно алгебраически складывать, если они обладают одинаковой размерностью. Чтобы сложить матрицу А с матрицей В, необходимо элемент первой строки первого столбца матрицы А сложить с первым элементом первой строки матрицы В, элемент второго столбца первой строки матрицы А сложить с элементом элемент второго столбца первой строки матрицы В и т.д.Свойства сложенияА+В=В+А(А+В)+С=А+(В+С)

Умножение матриц.

Матрицы можно перемножать, если они согласованы. Матрицы А и В считаются согласованными, если количество столбцов матрицы А равно количеству строк матрицы В.

Если А размерностью m на n, B размерностью n на к, то матрица С=А*В будет размерностью m на к и будет составлена из элементовГде С11 – сумма папарных произведений элементов строки матрицы А и столбца матрицы В, то есть элемента сумма произведения элемента первого столбца первой строки матрицы А с элементом первого столбца первой строки матрицы В, элемента второго столбца первой строки матрицы А с элементом первого столбца второй строки матрицы В и т.д.При перемножении важен порядок перемножения. А*В не равно В*А.

Нахождение определителя.

Любая квадратная матрица может породить определитель или детерминант. Записывает det. Или | элементы матрицы |Для матриц размерностью 2 на 2. Определить есть разница между произведением элементов главной и элементами побочной диагонали.Для матриц размерностью 3 на 3 и более. Операция нахождения определителя сложнее.Введем понятия:Минор элемента – есть определитель матрицы, полученной из исходной матрицы, путем вычеркивания строки и столбца исходной матрицы, в которой этот элемент находился.Алгебраическим дополнением элемента матрицы называется произведение минора этого элемента на -1 в степени суммы строки и столбца исходной матрицы, в которой этот элемент находился.Определитель любой квадратной матрицы равен сумме произведения элементов любого ряда матрицы на соответствующие им алгебраические дополнения.

Обращение матрицы

Обращение матрицы — это процесс нахождения обратной матрицы, определение которой мы дали в начале. Обозначается обратная матрица также как исходная с припиской степени -1.Находиться обратная матрица по формуле.А-1 = A*T x (1/|A|)Где A*T — Транспонированная матрица Алгебраических дополнений.

Примеры решения матриц мы сделали в виде видеоурока

:Если хотите разобраться, смотрите обязательно.

Это основные операции по решению матриц. Если появится дополнительные вопросы о том, как решить матрицы, пишите смело в комментариях.

В дополнении хотелось бы порекомендовать вам наш бесплатный сервис по решению матриц онлайн.

Если все же вы не смогли разобраться, попробуйте обратиться к специалисту.

iiikojiota.ru