ГлавнаяРазноеКоординатные точки

Как найти и записать координаты точки. Координатные точки


Как находить координаты точек?

Как находить координаты точек?

Навык находить координаты точки, понадобится не только для решения задач по математике, но и пригодится в жизни. Ведь это умение ориентироваться по карте, строить чертежи, работать в некоторых графических редакторах и даже играть в морской бой. В статье представлена информация о том, как находить координаты точек.

Математические оси

Координата точки - величины, которые определяют ее положение.Точка может располагаться на плоскости или в трехмерном пространстве. Любая плоскость имеет две величины. В математике это ось абсцисс и ординат, в географии – широта и долгота. На примере математической оси разберем, как находить координаты точек. Для того, чтобы найти координаты точки на плоскости необходимо сделать следующее:

  1. Чертим две оси, которые пересекаются под прямым углом. Точка их пересечения – это начала отсчета, то есть ноль. Горизонтальная ось соответствует оси абсцисс, она же ось X, а вертикальная – ось ординат или Y.
  2. Первой находим значение абсциссы. Для того этого опускаем перпендикуляр на горизонтальную ось. Это и есть ваше значение. Координата может иметь 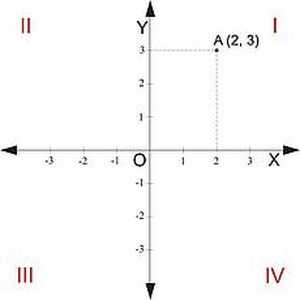вид положительного числа, если точка лежит справа от оси ординат и отрицательного – если она расположена слева. Бывает, что точка лежит на оси Y. Получается, что сама ось и есть наш перпендикуляр. То есть значение абсциссы равняется нулю.
  3. Приступаем к определению значения ординаты. Для этого проводим перпендикуляр на ось Y.  При расположении точки выше оси Х, это значение будет положительным, а ниже отрицательным. Если точка лежит на оси Х, то ордината точки равняется нулю.
  4. Координаты точки записываем в виде значений Х, Y, взятых в скобки. Например, если абсцисса равна 3, ордината – 4,5, то точка имеет координаты (3;-4,5).

Если перед вами стоит задача, как найти координаты точки в пространстве, она не так сложна, как кажется на первый взгляд. Все чем отличается определение значений заключается в введении дополнительной оси. То есть ваша точка будет иметь не 2, а 3 координаты. Обычно в математике третью ось называют Z. Если вам надо найти координаты точки, опус

elhow.ru

Как найти и записать координаты точки - Арифметика

каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости - это пара чисел, в которой на первомместе стоит абсцисса, а на втором - ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.

Точка пересечения с осью x называется абсциссой точки А, а с осью y называется ординатой точки А.

Обозначают координаты точки, как указано выше (•) A (2; 3).

Пример (•) A (2; 3) и (•) B (3; 2).

На первом месте записывают абсциссу (координату по оси x), а на втором - ординату (координату по оси y) точки.

Особые случаи расположения точек

  1. Если точка лежит на оси Oy, то её абсцисса равна 0. Например, точка С (0, 2).
  2. Если точка лежит на оси Ox, то её ордината равна 0. Например, точка F (3, 0).
  3. Начало координат - точка O имеет координаты, равные нулю O (0,0).
  4. Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
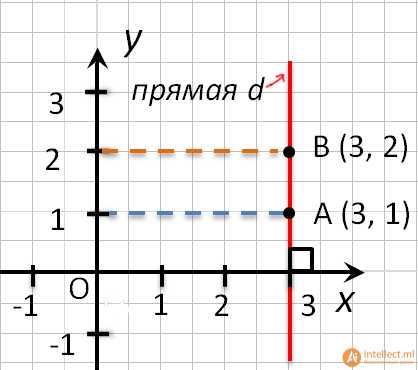
  5. Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
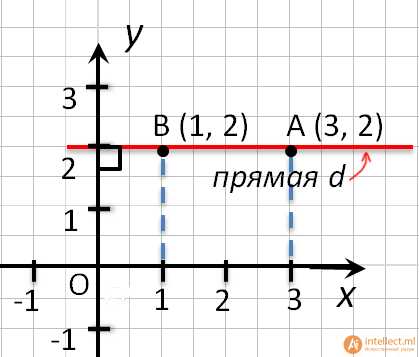
  6. Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
  7. Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

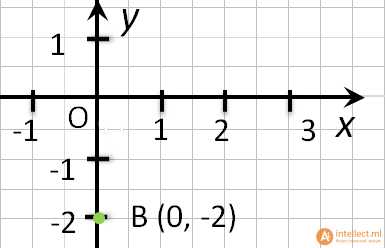
Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам, например, точки D (-4 , 2), надо:

  1. Отметить на оси Ox, точку с координатой (-4), и провести через неё прямую перпендикулярную оси 0x.
  2. Отметить на оси Oy, точку с координатой (2), и провести через неё прямую перпендикулярную оси 0y.
  3. Точка пересечения перпендикуляров (•) D - искомая точка. У неё абсцисса равна (-4), а ордината равна (2).

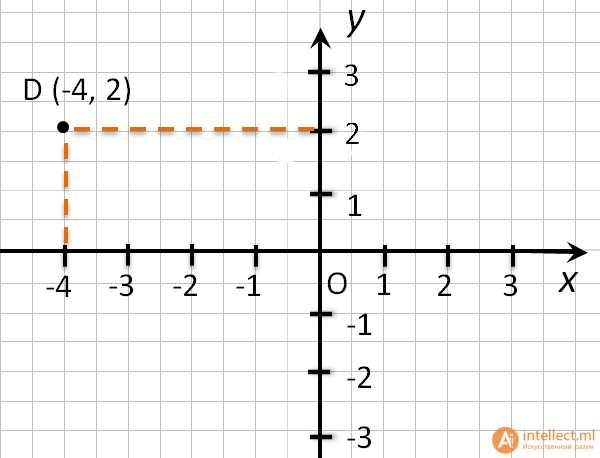
Второй способ

Чтобы найти точку D (-4 , 2) надо:

  1. Сместиться по оси x влево на 4 единицы, так как у нас перед 4 стоит «-».
  2. Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.

 

intellect.ml

Координатная точка правило — KAM-merch.ru

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на первом месте стоит абсцисса , а на втором — ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

  • Сместиться по оси « x » влево на 4 единицы, так как у нас перед 4 стоит « − ».
  • Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит « + ».

    • Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.

    math-prosto.ru

    Координатная прямая (числовая прямая), координатный луч.

    В этой статье мы определим координатный луч и координатную прямую. Сначала изобразим координатный луч и опишем, что он из себя представляет. Далее перейдем к координатной прямой, остановимся на взаимно однозначном соответствии между точками координатной прямой и действительными числами, откуда станет понятно, почему координатную прямую называют числовой прямой. В заключении поговорим о координатах точек на координатной прямой.

    Прежде чем переходить дальше, нужно иметь представление о точке и прямой, а также знать геометрическую фигуру луч.

    Навигация по странице.

    Координатный луч

    Чтобы определить координатный луч, нам сначала потребуется, конечно же, сам луч. Итак, построим луч, обозначим его OX , точка O – начало луча. Забегая вперед, скажем, что точку O называют началом отсчета координатного луча. Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала.

    Так у нас есть луч. Как же его сделать координатным лучом?

    Во-первых, над точкой O нужно написать число 0 .

    Во-вторых, нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1 .

    В-третьих, на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному, далее от конца этого отрезка нужно отложить еще один единичный отрезок, от конца построенного отрезка нужно отложить еще один единичный отрезок, и так далее.

    Наконец, чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из натурального ряда чисел: 2 , 3 , 4 , …

    Так координатный луч представляет собой не что иное, как бесконечную шкалу.

    Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O , и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа 0 и 1 . Этот вариант изображения координатного луча приведен на рисунке ниже.

    В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.

    Также допускается буквы O и X записывать над лучом, а числа – под лучом.

    Наконец, не удивляйтесь, если в обозначении координатного луча Вы увидите одновременно и маленькую и большую буквы. Наиболее часто придется сталкиваться с координатными лучами, обозначенными как Ox , Oy и Oz .

    Координатная прямая

    Координатную прямую очень легко построить, если Вы хорошо усвоили принцип изображения координатного луча, о котором мы говорили в предыдущем пункте. Сделаем это.

    Пусть перед нами находится координатный луч OX . Придадим ему положительное направление, указав его стрелочкой.

    Теперь проведем луч с началом в точке O , дополняющий луч OX до прямой.

    На этом луче отметим штрихи, откладывая друг за другом единичные отрезки справа налево, начиная с точки O .

    После того как над штрихами справа налево от точки O мы запишем числа -1 , -2 , -3 , …, координатная прямая примет законченный вид.

    На практике чаще используется координатная прямая, на которой отмечено лишь начало отсчета и единичный отрезок, то есть, координатная прямая одного из следующих видов.

    Итак, координатная прямая – это прямая, на которой выбрано начало отсчета, указан единичный отрезок и задано направление.

    Взаимно однозначное соответствие между точками координатной прямой и действительными числами

    Нам известно, что на данной прямой линии лежит бесконечно много точек. Не является исключением и координатная прямая – она также содержит бесконечно много точек. Между точками координатной прямой и действительными числами существует очень важная связь, которую называют взаимно однозначным соответствием. Эта связь выражается следующим утверждением: каждой точке координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.

    Озвученное утверждение, несомненно, нуждается в пояснении.

    Отметим какую-нибудь точку на координатной прямой. Какое действительное число ей соответствует?

    Если эта точка совпадает с началом отсчета (точкой O ), то будем считать, что ей отвечает число нуль.

    Если эта точка не совпадает с началом отсчета, то от точки O будем друг за другом последовательно откладывать единичные отрезки, пока не попадем в отмеченную точку. Если это произошло, то будем считать, что этой точке соответствует число, записанное над ней. Например, на рисунке ниже в точку М мы попадаем, отложив три единичных отрезка в отрицательном направлении, этой точке соответствует число -3 .

    Если же откладывание единичных отрезков на координатной прямой не приводит нас в отмеченную точку, то будем откладывать не только единичные отрезки, но и отрезки, составляющие одну десятую долю единичного отрезка, а при необходимости одну сотую долю, одну тысячную долю и так далее. На рисунке ниже в точку М мы попали, отложив в положительном направлении 1 единичный отрезок и 4 отрезка, составляющих десятую долю единичного отрезка. Этой точке соответствует рациональное число 1,4 . А если на координатной прямой отложить в отрицательном направлении 17 единичных отрезков, 3 отрезка, составляющих сотую долю единичного, и 9 отрезков, составляющих стотысячную долю единичного, то мы попадем в точку, которой будет соответствовать число, противоположное числу 17,03009 , то есть -17,03009 (при необходимости обращайтесь к материалу статьи противоположные числа).

    Так единичный отрезок и его десятая, сотая и так далее доли позволяют нам попасть в точки координатной прямой, которым будут соответствовать конечные десятичные дроби (как в предыдущем примере). Однако на координатной прямой существуют точки, в которые мы не можем попасть, но к которым мы можем подойти сколь угодно близко, использую все меньшие и меньшие до бесконечно малой доли единичного отрезка. Этим точкам соответствуют бесконечные периодические и непериодические десятичные дроби. Приведем несколько примеров. Одной из таких точек на координатной прямой соответствует число 3,711711711…=3,(711) . Чтобы подойти к этой точке нужно отложить 3 единичных отрезка, 7 его десятых долей, 1 сотую долю, 1 тысячную, 7 десятитысячных долей, 1 стотысячную, 1 миллионную долю единичного отрезка и так далее. А еще одной точке координатной прямой отвечает иррациональное число пи ( π=3,141592. ).

    Так как элементами множества действительных чисел являются все числа, которые можно записать в виде конечных и бесконечных десятичных дробей, то вся вышеизложенная в этом пункте информация позволяет утверждать, что каждой точке координатной прямой мы поставили в соответствие конкретное действительное число, при этом понятно, что разным точкам соответствуют разные действительные числа.

    Также достаточно очевидно, что это соответствие является взаимно однозначным. То есть, мы можем указанной точке на координатной прямой поставить в соответствие действительное число, но мы также можем по данному действительному числу указать конкретную точку на координатной прямой, которой отвечает данное действительное число. Для этого нам придется отложить от начала отсчета в нужном направлении определенное количество единичных отрезков, а также десятых, сотых и так далее долей единичного отрезка. Например, числу 703,405 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 703 единичных отрезка, 4 отрезка, составляющих десятую долю единичного, и 5 отрезков, составляющих тысячную долю единичного.

    Итак, каждой точке на координатной прямой отвечает действительное число, и каждое действительное число имеет свое место в виде точки на координатной прямой. Вот почему координатную прямую очень часто называют числовой прямой.

    Мимоходом заметим, что точкам, лежащим правее начала отсчета на числовой прямой, соответствуют положительные числа, а точкам, лежащим левее начала отсчета, — отрицательные. Подробнее об этом написано в статье положительные и отрицательные числа.

    Координаты точек на координатной прямой

    Число, соответствующее точке на координатной прямой, называется координатой этой точки.

    В предыдущем пункте мы сказали, что каждому действительному числу соответствует единственная точка на координатной прямой, поэтому, координата точки однозначно определяет положение этой точки на координатной прямой. Иными словами, координата точки однозначно задает эту точку на координатной прямой. С другой стороны каждой точке на координатной прямой соответствует единственное действительное число – координата этой точки.

    Осталось сказать лишь о принятых обозначениях. Координату точки записывают в круглых скобках справа от буквы, которой обозначена точка. Например, если точка М имеет координату -6 , то можно записать М(-6) , а запись вида означает, что точка М на координатной прямой имеет координату .

    www.cleverstudents.ru

    42. Координатная плоскость. Правила

    Чтобы обозначить числами точное положение точки на плоскости, проводят две перпендикулярные координатные прямые — x и y , которые пересекаются в начале отсчета — точке О (смотри рисунок). Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.

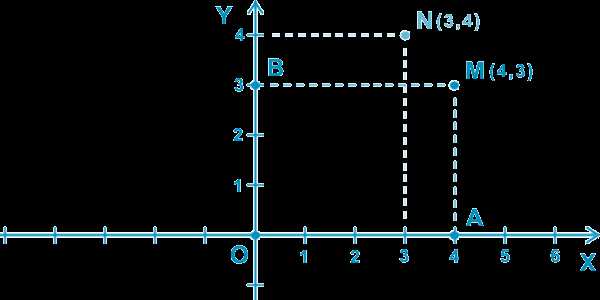
    Пусть M — некоторая точка плоскости. Проведем через нее прямую MA , перпендикулярную координатной прямой X , и прямую MB , перпендикулярную координатной прямой Y . Так как точка A имеет координату 4, а точка B координату 3 , то положение точки M определяется парой чисел (4, 3) . Эту пару чисел называют координатами точки M . Число 4 называют абсциссой точки M , а число 3 — ординатой точки M .

    Координатную прямую X называют осью абсцисс, а координатную прямую Y — осью ординат.

    Точку M с абсциссой 4 и ординатой 3 обозначают так: M (4, 3) . На первом месте пишут абсциссу точки, а на втором ее ординату.

    Если переставить координаты местами, то получится другая точка N (3, 4) , которая тоже изображена на рисунке.

    Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

    Задачи на тему «Координатная плоскость»

    M (1, 2) ; M (1, 3) ; M (2, 1) ; Неверно. Не кликай на пустое поле. Неверно. Неверно.

    M (2, –1) ; M (1, 2) ; M ( –1, 2) ; Неверно. Не кликай на пустое поле. Неверно. Неверно.

    M ( –4, 3) ; M (3, –4) ; M (–4, 2) ; Неверно. Не кликай на пустое поле.

    M (4, 2) ; M (2, 4) ; M (2, 5) ; Неверно. Неверно. Неверно. Не кликай на пустое поле.

    M (3, 5) ; M (5, 3) ; M (4, 3) ; Неверно. Неверно. Неверно. Не кликай на пустое поле. Неверно. Нeвeрнo. Задание выполнено. Неверно.

    school-assistant.ru

    Координатные плоскости и графики

    Прямоугольная система координат это пара перпендикулярных координатных линий, называемых осями координат, которые размещены так, что они пересекаются в их начале.

    Обозначение координатных осей буквами х и у является общепринятым, однако буквы могут быть любые. Если используются буквы х и у, то плоскость называется xy-плоскость. В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости и ts-плоскости.

    Упорядоченная пара

    Под упорядоченной парой действительных чисел мы имеем в виду два действительных чисел в определённом порядке. Каждая точка P в координатной плоскости может быть связана с уникальной упорядоченной парой действительных чисел путём проведения двух прямых через точку P: одну перпендикулярно оси Х, а другую — перпендикулярно оси у.

    Например, если мы возьмём (a,b)=(4,3), тогда на координатной полоскости

    Построить точку Р(a,b) означает определить точку с координатами (a,b) на координатной плоскости. Например, различные точки построены на рисунке внизу.

    В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке

    Определение графика

    Графиком уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения

    www.math20.com

    «Координаты. Координатная плоскость». 6-й класс

    Презентация к уроку

    Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

    Место урока в общей теме:

    Общая тема «Положительные и отрицательные числа»

    Это 1 урок по теме «Координаты»

  • организационный момент
  • актуализация
  • подготовка к активному и сознательному усвоению нового материала
  • усвоение нового материала
  • упражнения на понимание
  • обобщение и систематизация знаний
  • подведение итогов урока
  • оглашение домашнего задания

    • Ход урока

    I. Организационный момент.

    Приветствие. Постановка пред учащимися долговременных целей по теме и задач по уроку.

    II. Устная работа

    Направлена на подготовку учащихся к активному и сознательному усвоению нового материала.

    Координаты в жизненных ситуациях используются очень широко.

    1. Привести примеры того, как в жизни используются координаты.

    2. Предложить учащимся на основе рассмотренных примеров дать понятие координат.

    III. Изучение нового материала.

    1. Ввести понятие системы координат и координатной плоскости.

    Учащимся предлагается рассмотреть рисунок и рассказать, что на нем изображено или ответить на вопросы.

    — Можно ли утверждать, что на рисунке изображены координатные прямые? Почему?

    — Под каким углом расположены эти прямые к друг другу?

    — Охарактеризовать точку пересечения этих прямых.

    — Что напоминает запись ? Чем она отличается от записи координаты точки на координатной прямой?

    — Под каким углом из точки А проведены стрелки к координатным прямым и ?

    — Какая связь между точками координатных прямых, на которые указывают стрелки, и записью ?

    Выслушать ответы учащихся. Сделать выводы и ввести понятие системы координат, координатных осей, координатной плоскости, координат точки.

    Координаты точки – пара чисел, по которым определяется положение точки на плоскости, где на первом месте стоит абсцисса, а на втором — ордината этой точки.

    2. Ввести правило позволяющее определять координаты указанных точек.

    Учащимся предлагается рассмотреть рисунок и определить координаты отмеченных точек.

    Попросить учащихся сформулировать правило, позволяющее определить координаты точки. Повторить его.

    Чтобы определить координаты точки — надо из точки опустить перпендикуляры на координатные оси и определить, какому числу координатной оси соответствует основание перпендикуляра.

    Для закрепления этого правила учащимся предлагается самостоятельно определить координаты отмеченных точек координатной плоскости, изображенных на экране. А затем проверить свое решение с тем, что на экране.

    3. Определение положения точки на координатной плоскости по известным координатам.

    Учащимся дается точка с заданными координатами. Задание – по известным координатам определить положение точки на координатной плоскости.

    Сформулировать правило, позволяющее определять положение точки на координатной плоскости.

    Чтобы определить положение точки на координатной плоскости – надо провести прямые, перпендикулярные осям, и найти точку их пересечения.

    IV. Закрепление изученного материала.

    1. Учащимся предлагается построить координатную плоскость в тетрадях и отметить точки с указанными координатами, с последующей проверкой.

    2. Резервное задание. Найти площадь прямоугольника, если известны координаты его вершин.

    V. Подведение итогов урока. Выставление оценок.

    — Что нового узнали сегодня на уроке? Чему научились?

    — С какими понятиями познакомились?

    — Какие правила сегодня изучили?

    VI. Домашнее задание.

    Практическое задание: начертить на листе бумаги в клетку систему координат, взяв единичные отрезок длиной 1 см (две тетрадные клетки). Отметить произвольно десять точек, не указывая их координаты.

    xn--i1abbnckbmcl9fb.xn--p1ai

    Смотрите еще:

    kam-merch.ru

    Как найти координату точки

    Умение находить координаты точки позволит приступить к решению многих математических задач. Такие задачи носят прикладной характер, то есть широко используются на практике. Для понимания задач необходимо знание некоторых математических терминов.

    Вам понадобится

    - карандаш;- линейка.

    Спонсор размещения P&G Статьи по теме "Как найти координату точки" Как строить график координат Как найти основание трапеции, если известны диагонали Как определить центр массы

    Инструкция

    1

    Убедитесь, что точка расположена в системе координат. Координаты всегда определяются относительно чего-либо. Должна быть точка отсчета системы или "ноль". Относительно нее и определяются все остальные точки, расположенные в этой системе.

    Наиболее распространенной является декартова или прямоугольная система координат, расположенная на плоскости. Именно в ней мы и будем определять положение интересующей нас точки. У вас перед глазами должен быть ноль системы и две оси - X и Y, пересекающиеся в начале координат под прямым углом. Обычно ось X расположена по горизонтали, а ось Y - по вертикали.

    2

    Найдите абсциссу точки. Для этого проведите от точки перпендикуляр, до пересечения с осью X. Расстояние по оси X от начала координат до места пересечения и называется абсциссой. Она же - координата точки по оси X. Абсцисса может быть отрицательной, если пересечение произошло слева от оси Y, относительно нуля. Если точка расположена на оси Y, то абсцисса равна нулю.

    3

    Найдите ординату точки. Для этого проведите перпендикуляр от точки, до пересечения с осью Y. Расстояние по оси Y от начала координат до точки пересечения и называется ординатой. Она же - координата точки по оси Y. Ордината может быть отрицательной, если пересечение произошло ниже оси X, относительно нуля. Если точка расположена на оси X, то ордината равна нулю.

    4

    Запишите координаты точки. Они указываются в виде (X; Y), где вместо X и Y подставлены найденные значения абсциссы и ординаты. Например, точка имеет координаты (5; -7).

    Как просто

    masterotvetov.com

    Координаты точки и координаты вектора. Как найти координаты вектора

    Прямоугольная система координат

    Чтобы определить понятие координат точек нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка, в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.

    Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичные отрезки) – прямоугольная система координат в пространстве готова (рис. 1)

    Координаты точки

    Теперь разберем, как определяют в такой системе координат любой точки. Возьмем произвольную точку $M$ (рис. 2).

    Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).

    Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.

    Пример 1

    Записать координаты вершин параллелепипеда, изображенного на рисунке 4.

    Решение.

    Точка $O$ начало координат, следовательно, $O=(0,0,0)$.

    Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит

    $Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$

    Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит

    $S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$

    Точка $P$ имеет координаты $P=(2,2.5,1.5)$

    Координаты вектора

    Будем рассматривать далее введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $\overline{i}$, по направлению оси $Oy$ - единичный вектор $\overline{j}$, а по направлению оси $Oz$ - единичный вектор $\overline{k}$.

    Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).

    Теорема 1

    Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.

    Математически это выглядит следующим образом:

    $\overline{δ}=m\overline{α}+n\overline{β}+l\overline{γ}$

    Так как векторы $\overline{i}$, $\overline{j}$ и $\overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $\overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид

    $\overline{δ}=m\overline{i}+n\overline{j}+l\overline{k}$ (1)

    где $n,m,l∈R$.

    Определение 1

    Три вектора $\overline{i}$, $\overline{j}$ и $\overline{k}$ будут называться координатными векторами.

    Определение 2

    Коэффициенты перед векторами $\overline{i}$, $\overline{j}$ и $\overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть

    $\overline{δ}=(m,n,l)$

    Линейные операции над векторами

    Теорема 2

    Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.

    Доказательство.

    Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $\overline{α}=(α_1,α_2,α_3)$, $\overline{β}=(β_1,β_2 ,β_3)$.

    Эти вектор можно записать следующим образом

    $\overline{α}=α_1\overline{i}+ α_2\overline{j}+α_3\overline{k}$, $\overline{β}=β_1\overline{i}+ β_2\overline{j}+β_3\overline{k}$

    $\overline{α}+\overline{β}=α_1\overline{i}+ α_2\overline{j}+α_3\overline{k}+β_1\overline{i}+ β_2\overline{j}+β_3\overline{k}=(α_1+β_1 )\overline{i}+(α_2+β_2 )\overline{j}+(α_3+β_3)\overline{k}$

    Следовательно

    $\overline{α}+\overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$

    Теорема доказана.

    Замечание 1

    Замечание: Аналогично, определяется операция разности нескольких векторов.

    Теорема 3

    Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.

    Доказательство.

    Возьмем $\overline{α}=(α_1,α_2,α_3)$, тогда $\overline{α}=α_1\overline{i}+ α_2\overline{j}+α_3\overline{k}$, а

    $l\overline{α}=l(α_1\overline{i}+ α_2\overline{j}+α_3\overline{k})=lα_1\overline{i}+ lα_2\overline{j}+lα_3\overline{k}$

    Значит

    $k\overline{α}=(lα_1,lα_2,lα_3)$

    Теорема доказана.

    Пример 2

    Пусть $\overline{α}=(3,0,4)$, $\overline{β}=(2,-1,1)$. Найти $\overline{α}+\overline{β}$, $\overline{α}-\overline{β}$ и $3\overline{α}$.

    Решение.

    $\overline{α}+\overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$

    $\overline{α}-\overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$

    $3\overline{α}=(3\cdot 3,3\cdot 0,3\cdot 4)=(9,0,12)$

    spravochnick.ru

    Координаты точки и вектора — урок. Геометрия, 11 класс.

    Координаты точки

    Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.

     

     

    Оси координат \(Ox\), \(Oy\) и \(Oz\) называются соответственно: \(Ox\) — ось абсцисс, \(Oy\) — ось ординат, \(Oz\) — ось аппликат. 

    Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: \((Oxy)\), \((Oyz)\) и\((Oxz)\).

     

     

    Положение точки \(A\) в пространстве определяется тремя координатами: \(x\), \(y\) и \(z\).

     

     

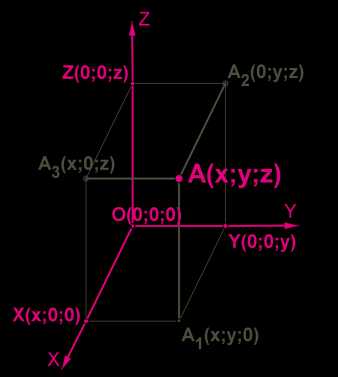
    Координата \(x\) называется абсциссой точки \(A\), координата \(y\) — ординатой точки \(A\), координата \(z\) — аппликатой точки \(A\).

    Записываются так: \(A(x; y; z)\).

    Если точка находится на оси \(Ox\), то её координаты \(X(x; 0; 0)\).

    Если точка находится на оси \(Oy\), то её координаты \(Y(0; y; 0)\).

    Если точка находится на оси \(Oz\), то её координаты \(Z(0; 0; z)\).

     

    Если точка находится в плоскости \(Oxy\), то её координаты A1x;y;0.

    Если точка находится в плоскости \(Oyz\), то её координаты A20;y;z.

    Если точка находится в плоскости \(Oxz\), то её координаты A3x;0;z.

    Координаты вектора

     

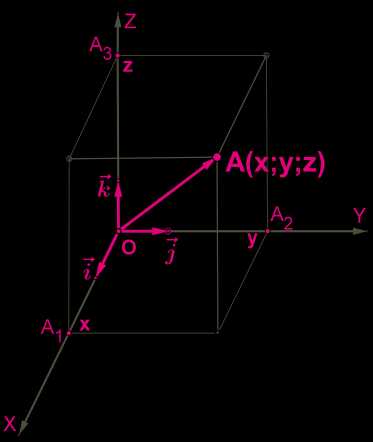
    Если в системе координат от начальной точки отложить единичные векторы i→, j→ и k→, то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в видеOA→=x⋅i→+y⋅j→+z⋅k→.

    Коэффициенты \(x\), \(y\) и \(z\) определяются одним единственным образом и называются координатами вектора.

     

    Записываются так: OA→x;y;z.

    Рассмотрим правила о том, как с помощью координат записать:

     

    - координаты суммы векторов, если даны координаты векторов:

    a→x1;y1;z1, b→x2;y2;z2, a→+b→x1+x2;y1+y2;z1+z2

     

    - координаты разности векторов, если даны координаты векторов: a→−b→x1−x2;y1−y2;z1−z2

     

    - координаты произведения вектора на число, если даны координаты вектора:

    n⋅a→n⋅x1;n⋅y1;n⋅z1

     

    - длину вектора:

    a→=x12+y12+z12

    - координаты вектора, если даны координаты начальной и конечной точки вектора:

    AxA;yA;zA, BxB;yB;zB, AB→xB−xA;yB−yA;zB−zA

     

    - расстояние между двумя точками, если даны координаты точек:

    AB→=AB=xB−xA2+yB−yA2+zB−zA2

     

    - координаты серединной точки отрезка, если даны координаты начальной и конечной точки отрезка:

    xC=xA+xB2;yC=yA+yB2;zC=zA+zB2

    www.yaklass.ru

    координата точки - это... Что такое координата точки?

     координата точки

     

    координата точки —[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]

    Тематики

    Справочник технического переводчика. – Интент. 2009-2013.

    Смотреть что такое "координата точки" в других словарях:

    technical_translator_dictionary.academic.ru