ГлавнаяРазноеНайти координаты центра тяжести треугольника

Как найти центр тяжести треугольника. Найти координаты центра тяжести треугольника


Как найти центр тяжести треугольника Как? Так!

Содержимое:

3 метода:

Центр тяжести треугольника (центроид) – это точка центра масс. Представьте себе треугольную линейку, положенную на кончик карандаша. Линейка будет балансировать, если кончик карандаша будет находиться в ее центре тяжести. Расположение центроида, которое легко находится с помощью геометрии, необходимо знать при работе над дизайнерским или инженерным проектом.

Шаги

Метод 1 Пересекающиеся медианы

  1. 1 Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.
    • Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см (10/2=5 2 Найдите середину второй стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой В.
      • Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см (12/2=6 3 Соедините середины сторон с противолежащими вершинами. Вы получите две медианы.
        • Вершина – это точка, в которой сходятся две стороны треугольника.
      • 4 Отметьте точку пересечения двух медиан. Эта точка является центром тяжести треугольника.
        • Центр тяжести находится на пересечении трех медиан, но так как медианы всегда пересекаются в одной точке, можно работать только с двумя медианами.

Метод 2 Отношение 2:1

  1. 1 Проведите медиану. Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Можно работать с любой медианой.
  2. 2 Измерьте длину медианы. Сделайте это аккуратно и точно.
    • Например, медиана равна 3,6 см.
  3. 3 Найдите третью часть (треть) медианы. Для этого разделите длину медианы на три. Сделайте это аккуратно и точно. Округлив полученное значение, вы не найдете центроид.
    • В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3: 3,6/3=1,2 4 Треть медианы отметьте точкой. Эта точка является центроидом, потому что он всегда делит медиану треугольника в отношении 2:1. То есть центр тяжести находится на расстоянии, которое равно ⅓ длины медианы, от середины стороны, или на расстоянии, которое равно ⅔ длины медианы, от вершины треугольника.
      • Например, если медиана равна 3,6 см, то центроид находится на расстоянии 1,2 см от середины стороны.

Метод 3 Усредненные координаты

  1. 1 Определите координаты трех вершин треугольника. Координаты могут быть даны; в противном случае будет дан треугольник, построенный на координатной плоскости. Координаты представляются в виде (x,y) 2 Сложите значения координат «х». Не забудьте сложить все три значения. Вы не найдете центр тяжести, если будете работать только с двумя значениями.
    • Например, если координаты «х» равны 3, 4 и 1, сложите эти значения: 3+4+1=8 3 Сложите значения координат «у». Не забудьте сложить все три значения.
      • Например, если координаты «у» равны 5, 1 и 0, сложите эти значения: 5+1+0=6 4 Найдите средние значения сумм координат «х» и «у». Полученные значения будут соответствовать центру тяжести треугольника. Чтобы найти среднее значение, разделите каждую сумму на 3.
        • Например, если сумма координат «х» равна 8, то среднее значение равно 8/3 5 Нанесите точку центра тяжести на треугольник. Центр тяжести находится в точке, координаты которой равны средним значениям сумм координат «х» и «у».
          • В нашем примере центр тяжести – это точка с координатами (8/3,2)

Прислал: DarK_Knigt . 2017-11-06 17:28:50

kak-otvet.imysite.ru

Геометрический центр тяжести » Аналитическая геометрия f(x)dx.Ru

п.5. ГЦТ системы из трех и более  материальных точек.

Пусть А, В, С – система из трех материальных точек с массами ,  и  соответственно. Заменим в этой системе две материальные точки, например, А и В материальной точкой D с массой , которая является их ГЦТ. Координаты точки D можно найти по формулам (15) и (16). Теперь у нас осталась система из двух материальных точек D и С с массами  и  соответственно. Обозначим через F их ГЦТ. Координату точки F опять можно найти по формулам (15) и (16), зная координаты точек D и С. Точка F называется ГЦТ системы из трех материальных точек А, В и С.

                     

                                         рис.5.

   Вообще ГЦТ системы из n () материальных точек определяется индукцией по их количеству.

Определение. ГЦТ системы из n () материальных точек  с массами  называется ГЦТ системы из двух материальных точек: С и  с массами  и  соответственно, где С – ГЦТ системы из -й материальных точек .

Теорема. (О ГЦТ системы из n материальных точек.)

Пусть  – система из n () материальных точек с массами  соответственно и С является их ГЦТ. Тогда для любой точки О верно равенство:

.                        (17)

Доказательство проводится методом математической индукции и предоставляется читателю.

   Также, как и в случае двух материальных точек из формулы (17) получаются следующие формулы.

Следствие. (О ГЦТ системы из n материальных точек.)

Пусть  – система из n () материальных точек с массами  соответственно и С является их ГЦТ. Тогда

,                                  (18)

,                                   (19)

.                                    (20)

п.6. ГЦТ треугольника.

   Пусть АВС треугольник, который мы будем рассматривать как треугольную пластинку, выполненную из однородного материала, толщиной которой мы пренебрежем. Известно, что центром тяжести такой пластинки является точка пересечения медиан.

   Рассмотрим теперь систему из трех материальных точек А, В и С с равными массами, сумма которых равна массе треугольника, т.е.

                           ,                             (21)

 где М – масса треугольника АВС.

   Из определения ГЦТ системы из двух материальных точек следует, что в данном случае ГЦТ материальных точек А и В равной массы лежит на середине отрезка АВ, которую мы обозначим буквой D. Действительно, по формуле (13) имеем:  и , т.е. D – середина АВ. Полагаем далее, что .

                      

                                             рис.6

   Пусть F – ГЦТ системы из двух материальных точек D и С. Тогда по формуле (13): , откуда следует, что , т.е. F является точкой пересечения медиан.

   С другой стороны, применяя формулы (18) – (20), получаем:

, ,                        (22)

.                                                           (23)

Определение. Точка пересечения медиан треугольника называется ГЦТ этого треугольника.

   Заметим, что точное определение ГЦТ геометрических фигур будет дано в курсе математического анализа при изучении кратных интегралов.

   Таким образом мы доказали теорему.

Теорема. ГЦТ из трех материальных точек с равными массами совпадает с ГЦТ треугольника с вершинами в данных точках.

   Как следствие, мы получили формулы (22), (23) для вычисления координат точки пересечения медиан треугольника, по известным координатам его вершин.

Возможно найдутся ответы здесь:

fxdx.ru

Определение координат центра тяжести плоских фигур (лабораторная работа), страница 10

         Общая длина дуги АВ будет равна

      .                                              (42)

         Подставим эти значения в первое уравнение (39). При этом интеграл, который находится в числителе данного выражения, должен быть определен по всей длине дуги.

Получаем

       (43)

         Таким образом, координата  будет равна

.                                  (44)

2.  Центр массы треугольника

Имеем треугольник, вершины которого в принятой системе координат  определяются точками с координатами  и (рис.13).

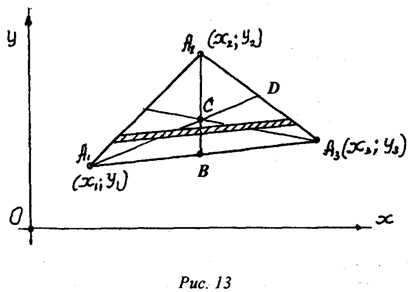
         Если провести достаточное количество прямых, которые параллельны основанию , то вся фигура треугольника будет разбита на полосы бесконечно малой ширины,  центры масс которых будут лежать посередине каждой из полученных полос. И поэтому центр массы треугольника будет лежать на его медиане . Далее, если провести линии, параллельные другой стороне треугольника, то и в этом случае центр массы будет лежать на его второй медиане . Также можно построить в треугольнике и третью медиану. Таким образом, вполне вероятно, что центр массы треугольника С будет размещен в точке пересечения трех его медиан, при этом =; СД=.

         Найдем координаты центра массы. Из аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями

                                        (45)

где   - координаты вершин треугольника.

3.  Центр массы сектора

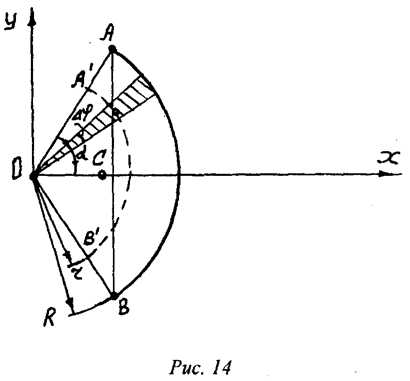
         Рассмотрим круговой сектор ОАВ радиусом R, центральный угол которого равен 2 радиан (рис.14). Центр массы сектора, вполне вероятно, лежит на оси его симметрии, то есть на биссектрисе угла АОВ. Эту биссектрису примем за ось  и найдем на этой оси  точку С.  Разобьем  площадь сектора на бесконечное число элементарных секторов с центральными углами . Будем рассматривать каждый сектор как угольник с основанием  и высотой R. Центры массы каждого такого треугольника лежат на расстоянии  от центра сектора. Таким образом, центры массы каждого треугольника расположены на дуге . Если  стремится к нулю (), то достаточно найти центр массы дуги . Согласно формулы (44) центр массы дуги  будет равен

.                              (46)

         Тогда, считая, что , получим

vunivere.ru

Центр тяжести - методы нахождения.

Методы нахождения центра тяжести



Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:

Рассмотрим приемы, применяемые в каждом из перечисленных методов.

***

Метод симметрии

Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).

В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда:

yC = Σ(Gixi)/ΣGi = 0.

Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.

Аналогично можно доказать и следующие положения:

***

Метод разбиения

Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.

Допустим, что мы разбили тело силой тяжести G на три части G', G'', G''', абсциссы центров тяжести этих частей x'C, x''C, x'''C известны. Формула для определения абсциссы центра тяжести всего тела:

xC = Σ(Gixi)/ΣGi.

Перепишем ее в следующем виде:

xCΣGi = Σ(Gixi)     или     GxC = Σ(Gixi).

Последнее равенство запишем для каждой из трех частей тела отдельно:

G'x'C = Σ(G'x'i),     G''x''C = Σ(G''ix''i),     G'''x'''C = Σ(G'''ix'''i).

Сложив левые и правые части этих трех равенств, получим:

G'x'C + G''x''C + G'''x'''C = Σ(G'ix'i) + Σ(G''x''i) + Σ(G'''ix'''i) = Σ(Gixi).

Но правая часть последнего равенства представляет собой произведение GxC, так как

GxC = Σ(Gixi),

Следовательно, xC = (G'x'C + G''x''C + G'''x'''C)/G, что и требовалось доказать. Аналогично определяются координаты центра тяжести на координатных осях y и z:

yC = (G'y'C + G''y''C + G'''y'''C)/G, zC = (G'z'C + G''z''C + G'''z'''C)/G.

Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi, а силы тяжести конечных частей; под координатами xi, yi, zi понимают координаты центров тяжести частей, на которые разбито тело.

***

Метод отрицательных масс

Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.

Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.

***

Практические методы определения центра тяжести тел

На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии. Затем вновь проводят линию вдоль нити. Точка пересечения двух линий и будет являться центром тяжести плоского тела.

Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт. Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю. Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов). По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести. Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а).

***



Положение центра тяжести некоторых фигур

Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.

Треугольник. Пусть дан треугольник АBD (см. рисунок 2). Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD. Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски), следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB, увидим, что искомый центр тяжести лежит и на медиане aD. Проделав аналогичное действие с треугольником относительно стороны ВD, получим тот же результат – центр тяжести находится на соответствующей медиане. Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.

Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.

Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда yC = 0 вследствие симметрии дуги относительно оси x. Определим координату центра тяжести xC.

Разобьем дугу АВ на элементарные части li, одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,

xC =Σ(lixCi)/Σli.

Дугу li вследствие малости примем за отрезок прямой. Из подобия треугольника ODiCi и элементарного треугольника S (на рисунке заштрихован) получим:

Li/Δyi = R/xCi     или     lixi = RΔyi.

Тогда:

xC =Σ(lixCi)/Σli = Σ(RΔyi)/l = RΣΔyi/l = R×AB/l,

поскольку RΣΔyi = AB, а Σli = l – длина дуги АВ. Но АВ = 2R sinα, а l = 2Rα, следовательно,

xC = (R sinα)/α.

При α = π/2 рад (полуокружность), xC = 2R/π.

Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а). Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда yC = 0.

Определим xC, для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги li можно принять за равнобедренный треугольник с высотой R. Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги. Очевидно, что

xC = 2 R sinα/(3α).

При α = π/2 рад (полукруг): xC = 4R/(3π).

***

Пример решения задачи на определение центра тяжести

Задача: Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4.

Решение. Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.

Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y, то центр тяжести такого сечения лежит на этой оси, т. е. xC = 0. По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.

Для двутаврового сечения:  А1 = 15,2 см2;     y1= 22/2 = 11 см. Для швеллерного сечения:  А2 = 12 см2;     y2 = 22 + d – z0= 22 + 0,32 – 1,25 = 21,07 см, где d – толщина стенки швеллера; z0 – размер, определяющий положение центра тяжести швеллера.

Применим формулу для определения координаты центра тяжести всего сечения:

yC = Σ(Aiyi)/ΣAi,

тогда:

yC = (A1y1 +A2y2)/(A1 +A2) = (15,2×11 + 12×21,07)/(15,2 + 12) = 15,4 см.

Задача решена.

***

Кинематика точки



k-a-t.ru

Как найти центр тяжести треугольника

Треугольник – одна из основных геометрических фигур. И только он имеет «замечательные» точки. К ним относится, например, центр тяжести – точка, на которую приходится вес всей фигуры. Где же находится эта «замечательная» точка и как ее найти?

Вам понадобится

карандаш, линейка

Спонсор размещения P&G Статьи по теме "Как найти центр тяжести треугольника" Как найти точку пересечения медиан треугольника Как определить координаты центра тяжести Как найти центр массы тела

Инструкция

1

Начертите сам треугольник. Для этого возьмите линейку и проведите карандашом отрезок. Потом начертите ещё один отрезок, начиная от одного из концов предыдущего. Замкните фигуру, соединив две оставшиеся свободные точки отрезков. Получился треугольник. Именно его центр тяжести предстоит искать.

2

Возьмите линейку и измерьте длину одной из сторон. Найдите середину этой стороны и отметьте её карандашом. Проведите отрезок из противоположной вершины к намеченной точке. Получившийся отрезок называется медианой.

3

Приступите ко второй стороне. Измерьте её длину, поделите на две равные части и проведите медиану из лежащей напротив вершины.

4

То же самое проделайте с третьей стороной. Обратите внимание на то, что, если вы все сделали правильно, то медианы пересекутся в одной точке. Это и будет центр тяжести или, как его ещё называют, центр масс треугольника.

5

Если перед вами стоит задача, найти центр тяжести равностороннего треугольника, то проведите высоту из каждой вершины фигуры. Для этого возьмите линейку с прямым углом и одной из сторон, прислоните к основанию треугольника, а вторую направьте к противолежащей вершине. То же самое проделайте с остальными сторонами. Точка пересечения будет являться центром тяжести. Особенность равносторонних треугольников заключается в том, что одни и те же отрезки являются и медианами, и высотами, и биссектрисами.

6

Центр тяжести любого треугольника делит медианы на два отрезка. Их соотношение составляет 2:1, если смотреть от вершины. Если треугольник поместить на булавку таким образом, что центроид окажется на её острие, то он не упадет, а будет находиться в равновесии. Также центр тяжести является той точкой, на которую приходится вся масса, размещенная на вершинах треугольника. Проделайте этот опыт и убедитесь в том, что эта точка неспроста называется «замечательной».

Как просто

masterotvetov.com

Как найти центр тяжести треугольника

Треугольник – одна из основных геометрических фигур. И только он имеет «замечательные» точки. К ним относится, например, центр тяжести – точка, на которую приходится вес всей фигуры. Где же находится эта «замечательная» точка и как ее найти?

Вам понадобится

Инструкция

completerepair.ru