ГлавнаяРазноеНечетные функции примеры

Чётные и нечётные функции. Нечетные функции примеры


Четные и нечетные функции

Четные функции

Определение 1

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться

\[f\left(x\right)=f(-x)\]

Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Рисунок 1.

Для исследования функции на четность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 1.

Нечетные функции

Определение 2

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться

\[f\left(-x\right)=-f(x)\]

Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

Рисунок 2.

Для исследования функции на нечетность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 2.

Функция общего вида

Определение 3

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть функцией общего вида, если она не будет ни четной, ни нечетной.

Для того чтобы понять, что данная функция является функцией общего вида, необходимо в его аналитической записи заменить переменную $x$ на переменную $--x$, произвести, при необходимости элементарные преобразования, и проверить невыполнение условий определений 1 и 2.

Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.

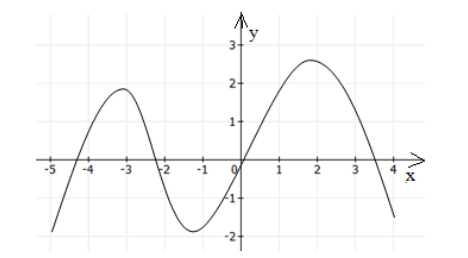
Рисунок 3.

Пример задачи

Пример 1

Исследовать функцию на четность и нечетность и построить их графики.

а) $f(x)=x^2+3$

б) $f(x)=\frac{x^2+4}{x}$

в) $f\left(x\right)=sinx+cosx$

Решение.

а) $f(x)=x^2+3$

$f\left(-x\right)={(-x)}^2+3=x^2+3=f(x)$\textit{ }следовательно, $f(x)$ -- четная функция.

Изобразим её на графике:

Рисунок 4.

б) $f(x)=\frac{x^2+4}{x}$

$f\left(-x\right)=\frac{{\left(-x\right)}^2+4}{-x}=-\frac{x^2+4}{x}$ следовательно, $f(x)$ -- нечетная функция.

Изобразим её на графике:

Рисунок 5.

в) $f\left(x\right)=sinx+cosx$

$f\left(-x\right)={\sin \left(-x\right)\ }+{\cos \left(-x\right)\ }=cosx-sinx$ следовательно, $f\left(x\right)$ -- функция общего вида.

Изобразим её на графике:

Рисунок 6.

spravochnick.ru

Чётные и нечётные функции - это... Что такое Чётные и нечётные функции?

 Чётные и нечётные функции

        Функция у = f (x) называется чётной, если она не меняется, когда независимое переменное изменяет только знак, то есть, если f (—x) = f (x). Если же f (—x) = — f (x), то функция f (x) называется нечётной. Например, у = cosx, у = x2— чётные функции, а = у sinx, у = x3— нечётные. График чётной функции симметричен относительно оси Оу, график нечётной функции симметричен относительно начала координат.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

Смотреть что такое "Чётные и нечётные функции" в других словарях:

dic.academic.ru

Чётная функция - это... Что такое Чётная функция?

 Чётная функция

f(x) = x — пример нечётной функции.

f(x) = x2 — пример чётной функции.

f(x) = x3, нечётная

f(x) = x3 + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Определения

Свойства

f(x) = g(x) + h(x),

где

Примеры

Нечётные функции

Чётные функции

Вариации и обобщения

Wikimedia Foundation. 2010.

Смотреть что такое "Чётная функция" в других словарях:

dic.academic.ru

Нечетная функция - это... Что такое Нечетная функция?

 Нечетная функция

f(x) = x — пример нечётной функции.

f(x) = x2 — пример чётной функции.

f(x) = x3, нечётная

f(x) = x3 + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Определения

Свойства

f(x) = g(x) + h(x),

где

Примеры

Нечётные функции

Чётные функции

Вариации и обобщения

Wikimedia Foundation. 2010.

Смотреть что такое "Нечетная функция" в других словарях:

dic.academic.ru

Чётные и нечётные функции - это... Что такое Чётные и нечётные функции?

 Чётные и нечётные функции

f(x) = x — пример нечётной функции.

f(x) = x2 — пример чётной функции.

f(x) = x3, нечётная

f(x) = x3 + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Определения

Свойства

f(x) = g(x) + h(x),

где

Примеры

Нечётные функции

Чётные функции

Вариации и обобщения

Wikimedia Foundation. 2010.

Смотреть что такое "Чётные и нечётные функции" в других словарях:

dic.academic.ru

Чётность функции - Gpedia, Your Encyclopedia

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

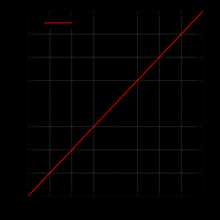f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная

Строгое определение

Определения вводятся для любой симметричной относительно нуля области определения X⊂R{\displaystyle X\subset \mathbb {R} }, например, отрезка или интервала.

f(−x)=f(x),∀x∈X.{\displaystyle f(-x)=f(x),\quad \forall x\in X.}f(−x)=−f(x),∀x∈X.{\displaystyle f(-x)=-f(x),\quad \forall x\in X.}

Свойства

f(x)=g(x)+h(x),{\displaystyle f(x)=g(x)+h(x),} где g(x)=f(x)−f(−x)2,h(x)=f(x)+f(−x)2.{\displaystyle g(x)={\frac {f(x)-f(-x)}{2}},\;h(x)={\frac {f(x)+f(-x)}{2}}.}∫−AAf(x)dx=2∫0Af(x)dx=2∫−A0f(x)dx.{\displaystyle \int \limits _{-A}^{A}f(x)\;dx=2\int \limits _{0}^{A}f(x)\;dx=2\int \limits _{-A}^{0}f(x)\;dx.} Соответственно, для определённых интегралов от нечётных функций выполняется равенство ∫−AAf(x)dx=0.{\displaystyle \int \limits _{-A}^{A}f(x)\;dx=0.}∫−∞∞f(x)dx=2∫0∞f(x)dx=2∫−∞0f(x)dx{\displaystyle \int \limits _{-\infty }^{\infty }f(x)\;dx=2\int \limits _{0}^{\infty }f(x)\;dx=2\int \limits _{-\infty }^{0}f(x)\;dx} и от нечётных функций: v.p.∫−∞∞f(x)dx=0{\displaystyle \mathrm {v.p.} \int \limits _{-\infty }^{\infty }f(x)\;dx=0} (v. p. обозначает главное значение несобственного интеграла по Коши).

Примеры

Ниже везде x∈R.{\displaystyle x\in \mathbb {R} .}

Нечётные функции

Чётные функции

Литература

www.gpedia.com

Нечётная функция Википедия

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная

Строгое определение

Определения вводятся для любой симметричной относительно нуля области определения X⊂R{\displaystyle X\subset \mathbb {R} }, например, отрезка или интервала.

f(−x)=f(x),∀x∈X.{\displaystyle f(-x)=f(x),\quad \forall x\in X.}f(−x)=−f(x),∀x∈X.{\displaystyle f(-x)=-f(x),\quad \forall x\in X.}

Свойства

f(x)=g(x)+h(x),{\displaystyle f(x)=g(x)+h(x),} где g(x)=f(x)−f(−x)2,h(x)=f(x)+f(−x)2.{\displaystyle g(x)={\frac {f(x)-f(-x)}{2}},\;h(x)={\frac {f(x)+f(-x)}{2}}.}∫−AAf(x)dx=2∫0Af(x)dx=2∫−A0f(x)dx.{\displaystyle \int \limits _{-A}^{A}f(x)\;dx=2\int \limits _{0}^{A}f(x)\;dx=2\int \limits _{-A}^{0}f(x)\;dx.} Соответственно, для определённых интегралов от нечётных функций выполняется равенство ∫−AAf(x)dx=0.{\displaystyle \int \limits _{-A}^{A}f(x)\;dx=0.}∫−∞∞f(x)dx=2∫0∞f(x)dx=2∫−∞0f(x)dx{\displaystyle \int \limits _{-\infty }^{\infty }f(x)\;dx=2\int \limits _{0}^{\infty }f(x)\;dx=2\int \limits _{-\infty }^{0}f(x)\;dx} и от нечётных функций: v.p.∫−∞∞f(x)dx=0{\displaystyle \mathrm {v.p.} \int \limits _{-\infty }^{\infty }f(x)\;dx=0} (v. p. обозначает главное значение несобственного интеграла по Коши).

Примеры

Ниже везде x∈R.{\displaystyle x\in \mathbb {R} .}

Нечётные функции

Чётные функции

Литература

wikiredia.ru