Неравенства с модулем и их решение. Неравенство с модулем решение
Неравенства с модулем, примеры решений
Схема решения простейших неравенств:
1) неравенство вида при равносильно системе ; при неравенство решений не имеет.
2) неравенство , при равносильно совокупности неравенств
при решением неравенства является множество ; – вся числовая ось, то есть .
При решении неравенства вида или , обе части неравенства возводят в квадрат. Если неравенство содержит несколько выражений под знаком модуля, то применяется метод интервалов.
Примеры
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Решение неравенств с модулем. Модуль раскрытие. Неравенства содержащие модуль. Неравенства с модулем примеры решения.
Как решать неравенства с модулем?
Методы решения систем линейных неравенств отличаются от методов решения линейных уравнений тем, что знаки неравенства не позволяют выполнять подстановку, как мы это делаем с уравнениями. Тем не менее, мы решаем по определенной системе. Система линейных неравенств включает в себя несколько выражений, которые при решении могут дать ряд решений.
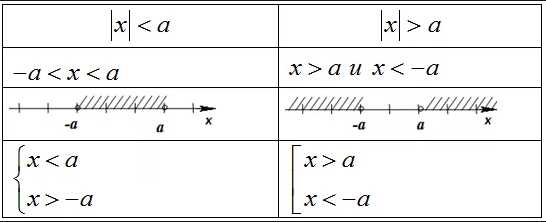
\(|x|\)— расстояние на числовой прямой от \(0\) до точки \(a\).
- \(|u|=u\) \(-->\) \(u\geq0\)
- \(|u|=-u\) \(-->\) \(u\le \: 0\)
- \(|u|=|v|\) \(-->\) \(v^2=u^2\)
- \(|x|<a \) \(-->\) \(-a<x<a\) Система
- \(|x|\le \:a \) \(-->\) \(-a\le \:x\le \:a\)
- \(|x|> a \) \(-->\) \(\left[ \begin{gathered} x < -a \\ x >a \\ \end{gathered} \right.\) Совокупность
- \(|x|\geq a \) \(-->\) \(\left[ \begin{gathered} x \le \: -a \\ x \geq a \\ \end{gathered} \right.\)
Пример 1. Решить неравенство \(|3+x| \geq|x|\).
Решение. \(|3+x| \geq|x|\)\(-->\) \((3+x)^2\geq x^2\) \(-->\) \(x^2+6x+9\geq x^2\) \(-->\) \(6x\geq -9\) \(-->\) \(x\geq -1,5\)
Ответ: \([-1,5; +∞)\)
Пример 2. Решить неравенство \(\left|3+2x\right|\le \:7\). Система
Решение. \(\left|3+2x\right|\le \:7\) \(-->\) \(3+2x\le \:7\) и \(3+2x\ge \:-7\) или \(-7\le \:3+2x\le \:7\)
\(x\le \:2\) и \(x\ge \:-5\) \(-5\le \:x\le \:2\)
Ответ: [-5;2];
Пример 3. Решить неравенство \(\left|3x-5\right|<\:4\)
Решение: \(-4<3x-5<4\) \(-->\) \(\frac{1}{3}<x<3\)
Ответ: \((\frac{1}{3};3)\);
Пример 4. Решить неравенство \(\left|x-8\right|\ge \:\:3\)
Решение: Совокупность \(\) \(\left[ \begin{gathered} x-8\le \:-3\\ x-8\ge \:3 \\ \end{gathered} \right.\) \(-->\) \(\left[ \begin{gathered} x\le \:5\\ x\ge \:11 \\ \end{gathered} \right.\)
Ответ: \((+∞;5)⋃ (11;+∞)\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
5.4. Неравенства с модулем
Рассмотрим некоторые виды неравенств, содержащих знак модуля, и методы их решения.
1. 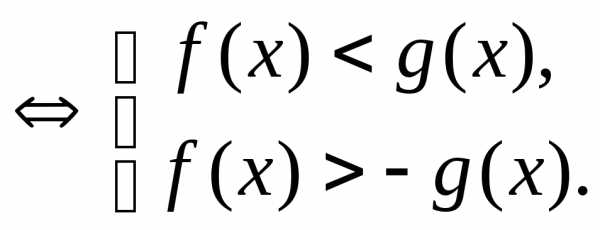
В частности, 
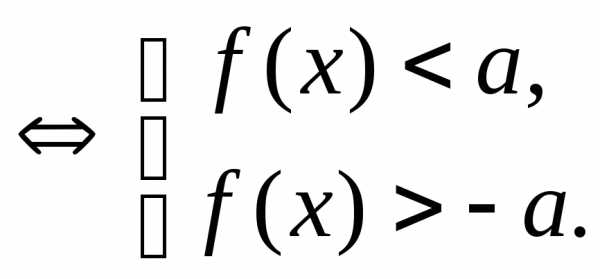 , где
, где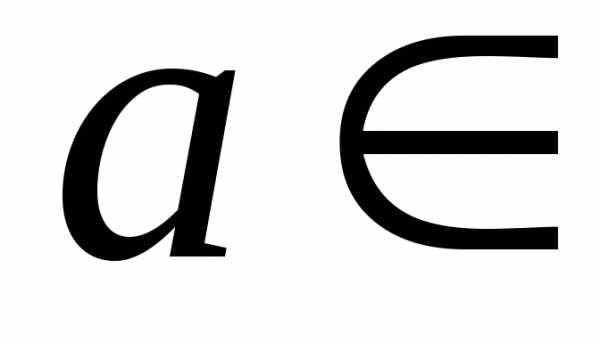
 ,
, . При
. При неравенство решений не имеет.
неравенство решений не имеет.
2. 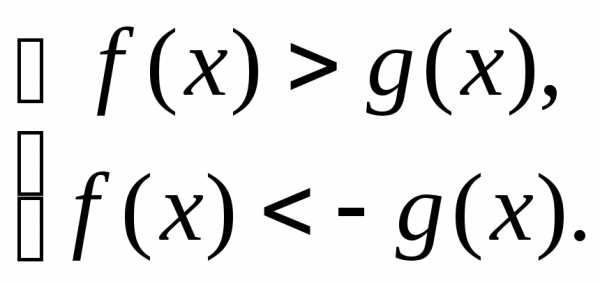
В частности, 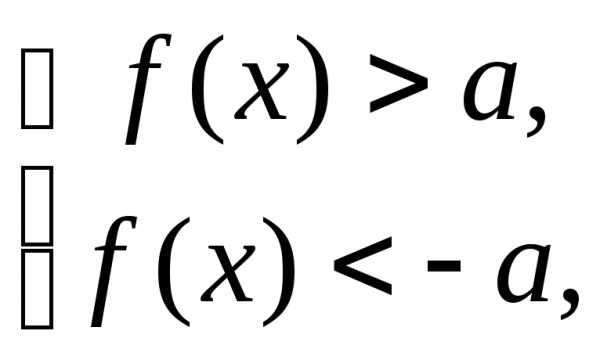
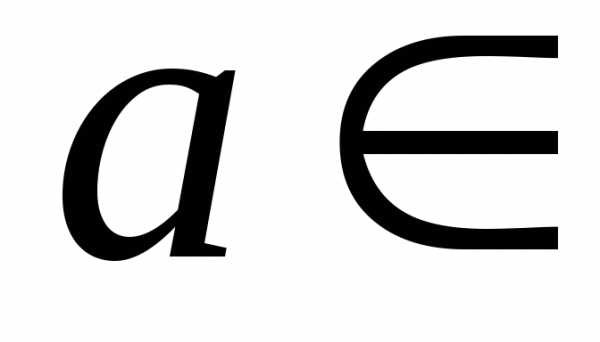
 ,
, . При
. При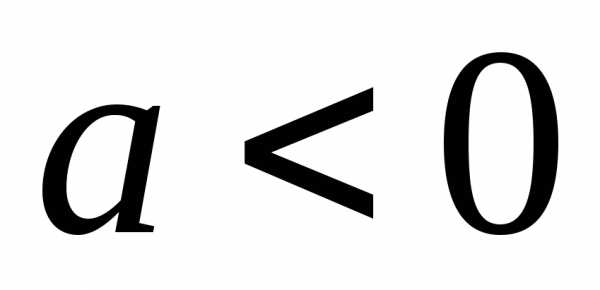 неравенство выполняется для всех
неравенство выполняется для всех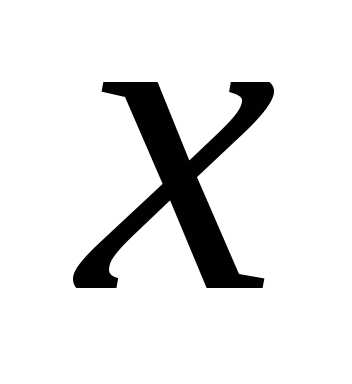 при которых функция
при которых функция определена.
определена.
3.
.
Последнее неравенство решается методом интервалов.
4. Неравенство вида  решают с помощью замены.
решают с помощью замены.
Пример 5.6. Решить неравенство  .
.
Решение. .
Ответ: 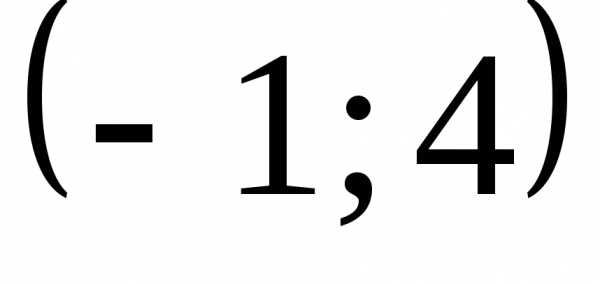 .
.
Пример 5.7. Решить неравенство  .
.
Решение. 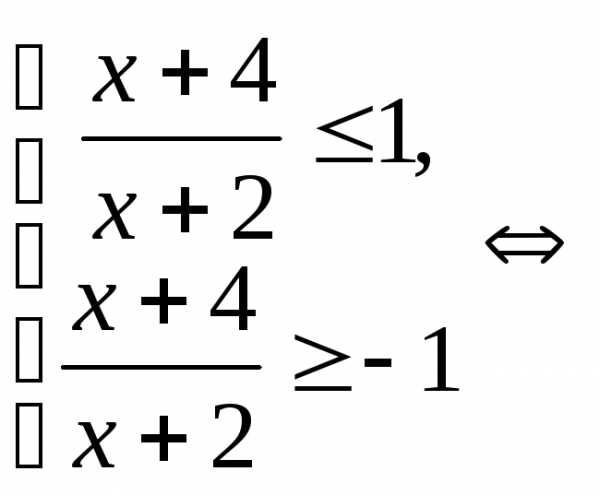


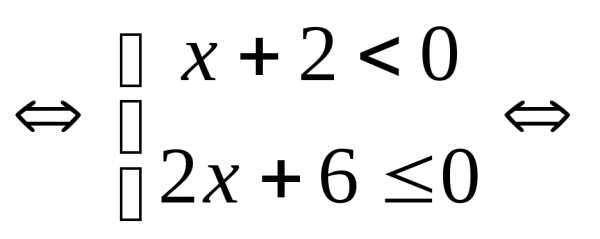
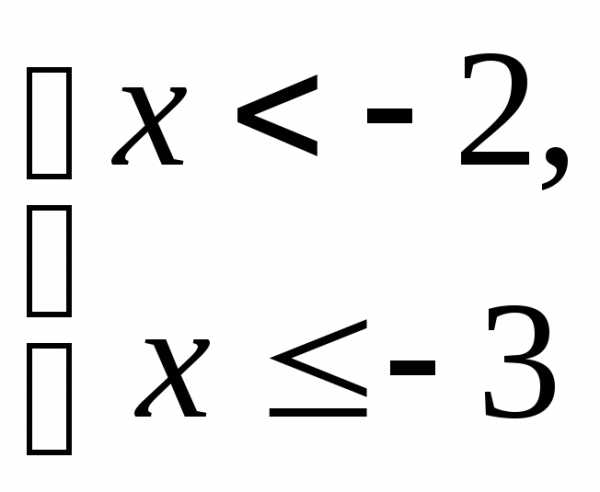 .
.
Ответ: 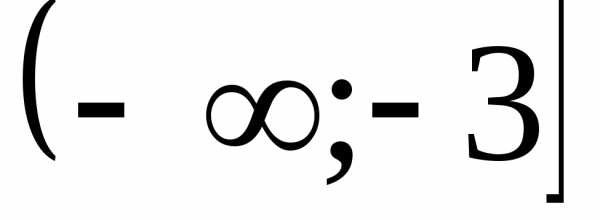 .
.
Пример 5.8. Решить неравенство .
Решение.
.
Ответ: .
Пример 5.9. Решить неравенство .
Решение.
 .
.
Ответ: .
Пример 5.10. Решить неравенство .
Решение. Из свойств модуля следует, что . Поэтому
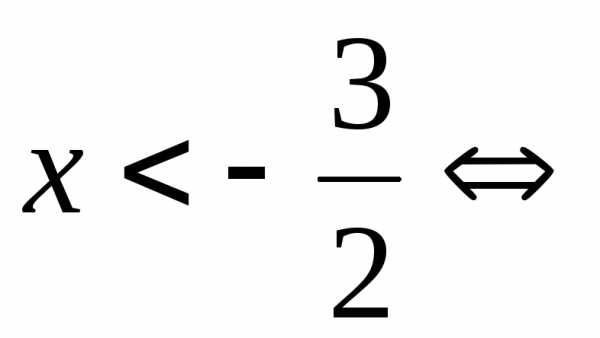
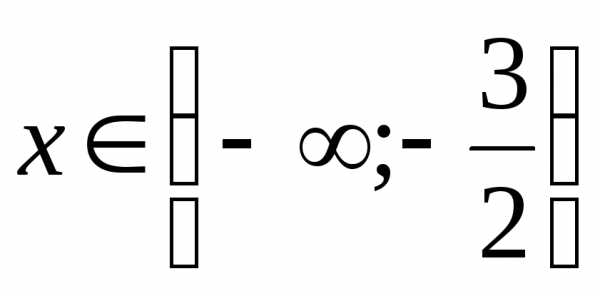 .
.
Ответ: 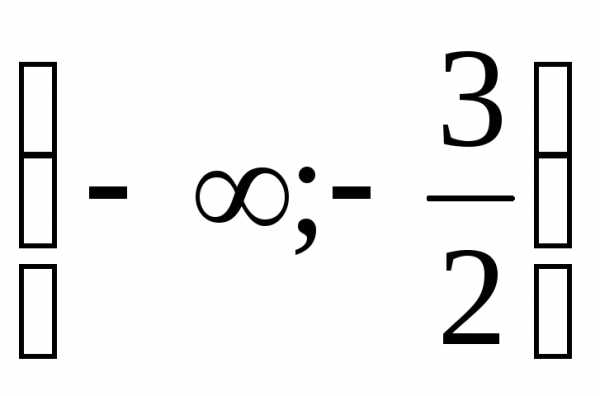 .
.
Пример 5.11. Решить неравенство .
Решение.

Ответ:  .
.
Пример 5.12. Решить неравенство .
Решение. Введем замену , тогда исходное неравенство имеет вид:
.
Переходя обратно к переменной 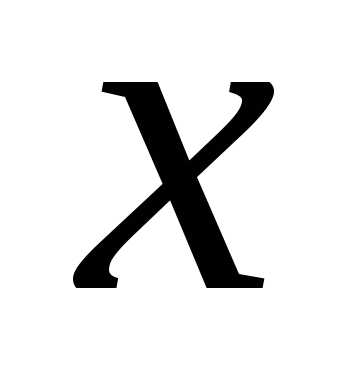 , получим:
, получим:
 .
.
Ответ: .
Пример 5.13. Решить неравенство .
Решение.
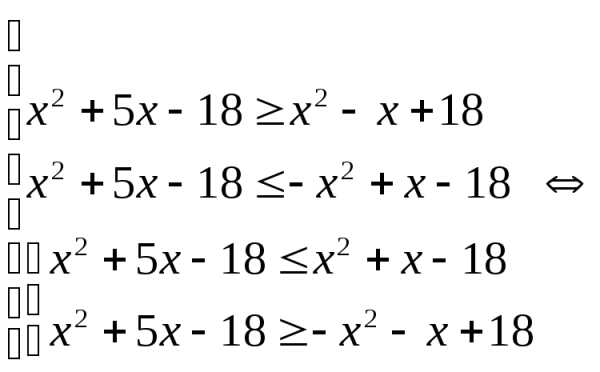
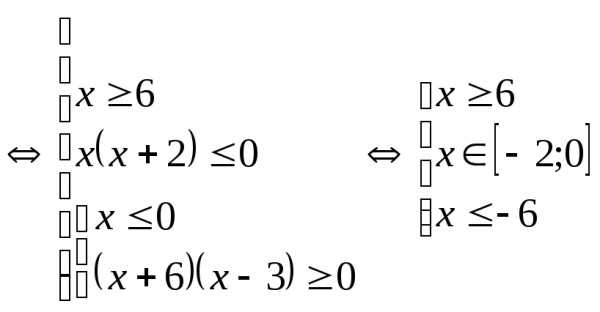 .
.
Ответ: .
Пример 5.14. Решить неравенство .
Решение.
.
Ответ: .
5.5. Иррациональные неравенства
К основным методам решения иррациональных неравенств относятся:
1. сведение исходного неравенства к равносильной системе рациональных неравенств или к совокупности неравенств:
a) 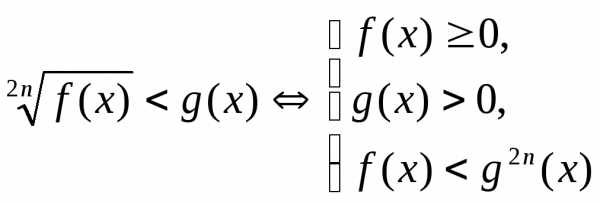 ,
,
в частности, для 
 ,
, 
б) ,,
в частности, для 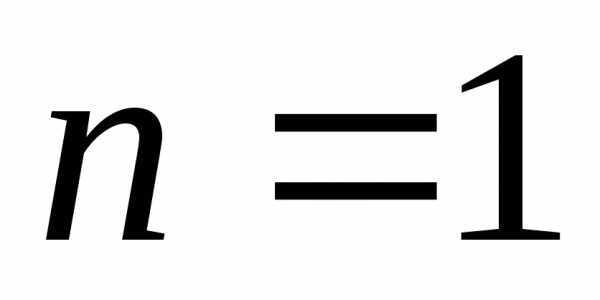
,
б) ,
в частности, для 
, ;
2. введение новой переменной;
3. ,
4.
Пример 5.15. Решить неравенство .
Решение.
 .
.
Ответ:  .
.
Пример 5.16. Решить неравенство .
Решение. 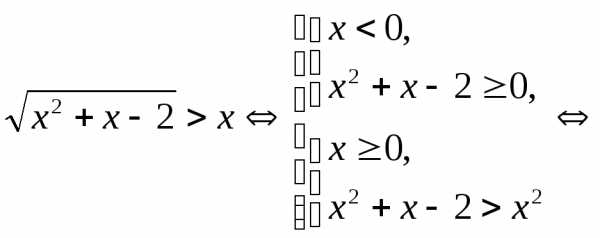
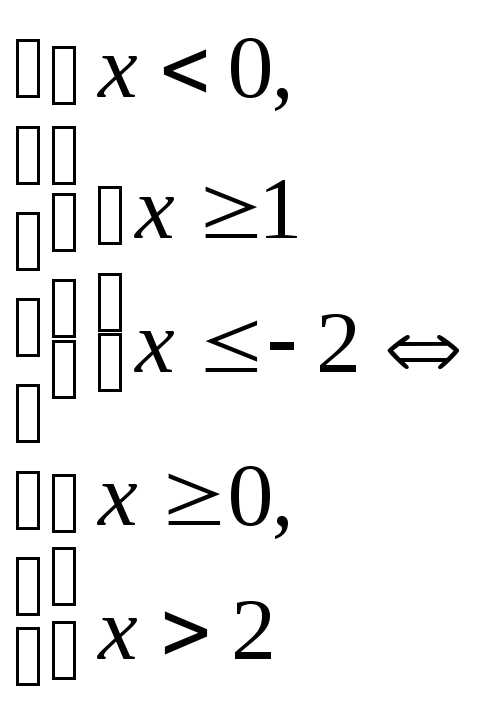
.
Ответ: .
Пример 5.17. Решить неравенство
.
Решение.
,
последняя система, а, следовательно, и исходное неравенство, решений не имеет.
Ответ: решений нет.
Пример 5.18. Решить неравенство .
Решение.
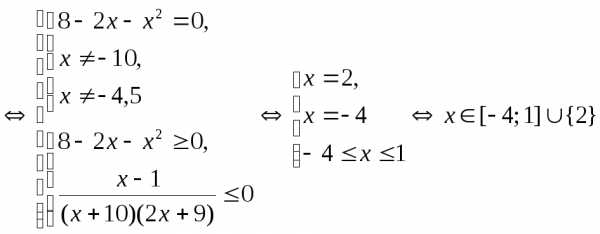 .
.
Ответ: .
Задачи для самостоятельного решения Группа а
1. Укажите длину промежутка, который является решением неравенства:
 (Ответ:
(Ответ:  .)
.)
2. Найти произведение всех целых решений неравенства:
. (Ответ:  .)
.)
Решить неравенство (3-15)
3. . (Ответ:  .)
.)
4. (Ответ: .)
5. (Ответ: 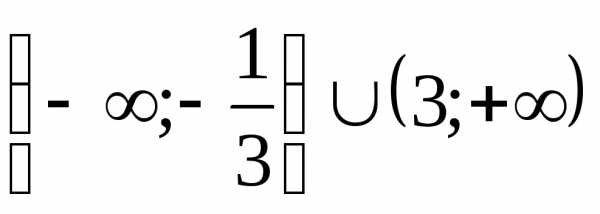 .)
.)
6. 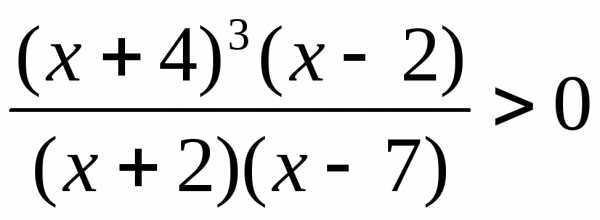 . (Ответ: .)
. (Ответ: .)
7. 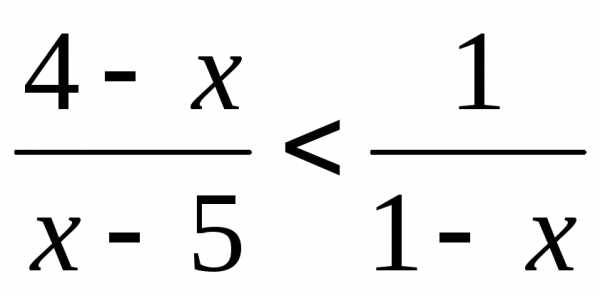 . (Ответ: .)
. (Ответ: .)
8. . (Ответ:  .)
.)
9. 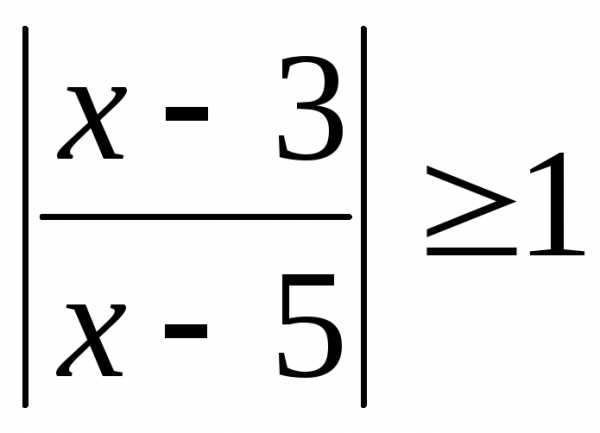 . (Ответ: .)
. (Ответ: .)
10. . (Ответ:  .)
.)
11. . (Ответ: 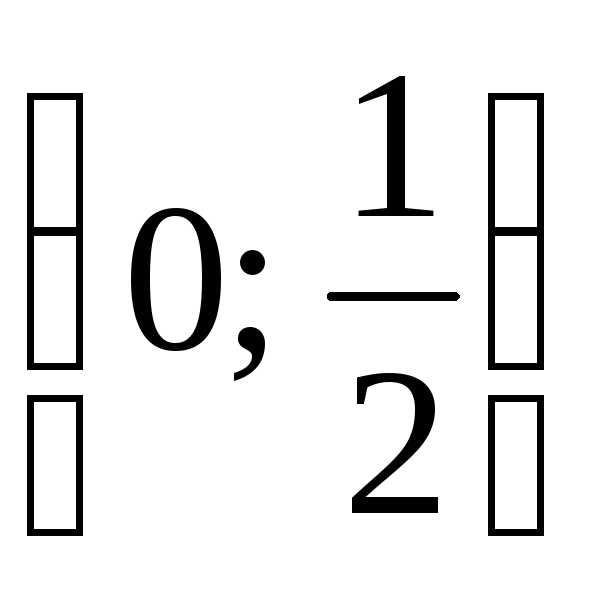 .)
.)
12. . (Ответ: .)
13. . (Ответ:  .)
.)
12. . (Ответ: 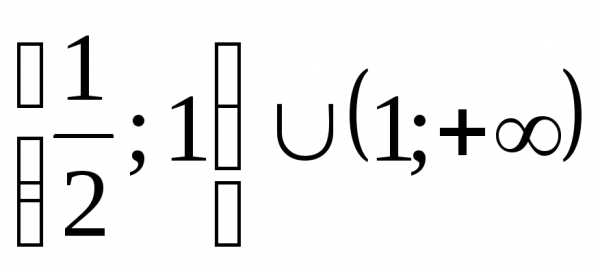 .)
.)
13. . (Ответ: .)
14. . (Ответ: .)
15. . (Ответ:  .)
.)
studfiles.net
Решение неравенств с модулем | Математика, которая мне нравится
Для решения неравенств с модулем следует раскрыть модуль так же, как это делалось при решении уравнений, а затем решить полученные неравенства на соответствующих множествах (иными словами, решить полученные системы неравенств).
Пример 1. Решить неравенство
Решение. Рассмотрим два случая: 1) и 2) .
1) В этом случае неравенство равносильно системе
Преобразуя первое неравенство к виду , получим (см. рис. 13):
Рис. 13
Решение неравенства (-\infty;0]\cup[5;+\infty).
Преобразуя второе неравенство , получим (см. рис. 14):
Рис. 14
Решение неравенства . Решением системы является пересечение решений неравенств, то есть .
2) В этом случае неравенство равносильно системе:
Решение первого неравенства (см. рисунок к случаю 1)). Неравенство преобразуется к , его решение (см. рис. 15):
Рис. 15
Решение системы — пересечение множеств решений двух неравенств, то есть .
Общее решение исходного неравенства — объединение решений обоих случаев.
Ответ. .
Замечание. В данном случае проще было из определения модуля получить двойное неравенство , а затем его решить.
Пример 2. Решить неравенство
Решение. Точки и (корни выражений, стоящих под модулем) разбивают всю числовую ось на три интервала, на каждом из которых следует раскрыть модули.
1) При выполняется , и неравенство имеет вид , то есть . В этом случае ответ .
2) При выполняется , неравенство имеет вид , то есть . Это неравенство верно при любых значениях переменной , и, с учетом того, что мы решаем его на множестве , получаем ответ во втором случае .
3) При выполняется , неравенство преобразуется к , и решение в этом случае . Общее решение неравенства — объединение трех полученных ответов.
Ответ. .
Задачи. Решите неравенства:
1. .
2. .
3. .
4. .
hijos.ru
25. Неравенства с модулем | Решение задач по математике и другим предме
I тип: Неравенство содержит некоторое выражение под модулем и число вне модуля:
где (3.27)
Решение зависит от знака числа А.
1. Если то неравенство (3.27) не имеет решений.
2. Если то неравенство (3.27) равносильно системе неравенств
где (3.28)
1. Если то неравенство (3.28) не имеет решений.
2. Если то неравенство (3.28) равносильно уравнению
3. Если , то неравенство (3.28) равносильно системе неравенств
где (3.29)
1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что
3. Если то неравенство (3.29) равносильно совокупности
где (3.30)
1. Если то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения
2. Если то неравенство (3.30) равносильно совокупности
II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:
(3.31)
Где – некоторые выражения с переменной Х.
Для решения неравенств типа (3.31) можно использовать следующие способы.
1-й способ: используя определение модуля, получаем равносильную совокупность систем:
2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения
1. Если
(3.32)
То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32).
2. Если
То решением является множество всех значений Х, которые удовлетворяют системе
3. Если решение определяется системой
Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3.
3-й способ: метод интервалов.
Для решения необходимо:
1) найти значения Х, для которых
2) найденные значения Х нанести на числовую ось;
3) определить знак выражения на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
III тип: Неравенство содержит несколько модулей и решается двумя способами:
1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.
2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.
IV тип: Неравенство вида
где (3.33)
Решается двумя способами:
1-й способ: метод интервалов.
2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:
Решение неравенства (3.33) сводится к решению неравенства
Аналогично решают неравенства IV типа (3.33), если они заданы со знаками
V тип: Неравенства, решаемые заменой переменной.
В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.
Пример 1. Решить неравенства:
1) 2)
3) 4)
5) 6)
Решение. 1) Решаем как неравенство I типа:
Получаем ответ:
2) Решаем как неравенство I типа:
Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду
Его решение: это и есть ответ.
3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему:
Получаем ответ:
4) Заданное неравенство может быть записано в виде
Заменим переменную Решаем неравенство
Его решение
Возвращаемся к переменной Х и решаем совокупность
Получаем
Т. е. приходим к ответу
5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде
Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).
ОДЗ:
Рис. 3.10
А) рассмотрим неравенство на 1-м промежутке. Получаем систему
(3.34)
Решаем неравенство
Получаем
Система (3.34) сводится к системе
На данном промежутке решений нет.
Б)
Если , то С учетом рассматриваемого промежутка имеем:
Получаем
В)
Решением является промежуток:
Объединим полученные решения и приходим к ответу:
6)
ОДЗ:
Введем новую переменную:
тогда и приходим к неравенству вида
Решаем его
Используем метод интервалов (рис. 3.11).
Рис. 3.11
Запишем полученное решение в виде совокупности:
Вернемся к переменной Х:
(3.35)
– выполняется при любых
С учетом ОДЗ второе неравенство системы (3.35) равносильно системе
Получаем ответ:
| Следующая > |
matica.org.ua
Репетитор по математике и физике » Уравнения и неравенства с модулем

Репетитору по математике часто приходится сталкиваться с отсутствием у старшеклассников навыков решения простейших уравнений и неравенств с модулем. Между тем среди заданий С3 или С5 из ЕГЭ по математике таковые могут встретиться. Даже если их не будет на экзамене в явном виде, в процессе выполнения некоторых задач из ЕГЭ вам, возможно, придется столкнуться с решением того или иного задания с модулем. Поэтому научиться решать уравнения и неравенства с модулем должен каждый выпускник средней школы. В данной статье рассмотрены некоторые способы их решения. Присутствует также видеоразбор решения одного уравнения, содержащего модуль.
Считается, что чем больше способов решения существует у задачи, тем она интереснее с математической точки зрения. Уравнения и неравенства с модулями можно поэтому смело назвать интересными. Рассмотрим пример.
Решите уравнение:
Решение. Постараемся найти как можно большее количество решений данного уравнения. Подробное объяснение решений смотрите в видеоуроке.
Способ №1. Решение возведением в квадрат. Просто возводим обе части уравнения в квадрат. При этом не забываем, что подобное преобразование не является равносильным. Из-за этого могут появиться посторонние корни, поэтому полученные решения необходимо будет проверить прямой подстановкой в исходное уравнение.
Путем прямой подстановки полученных решений в исходное уравнение убеждаемся, что посторонних корней среди них нет. На самом деле в данном конкретном задании отсутствует необходимость проверки корней. Возведение обеих частей этого уравнения в квадрат не может привести к приобретению посторонних решений. Подумайте самостоятельно, почему это так.
Способ №2. Метод интервалов. Не совсем верное название, но мы его здесь употребим, поскольку в методической литературе оно встречается. Для решения нам потребуется найти значение переменной при котором подмодульное выражение обращается в ноль: Наносим эту точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.
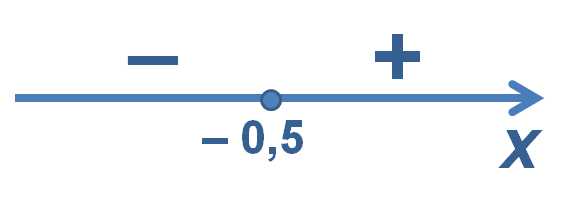
Числовая прямая
Далее на каждом промежутке раскрываем знак модуля в соответствии с полученными данными:
Способ №3. Замена уравнения смешанной системой. Известно, что:
Для тех, кто не знает, какой именно смысл вкладывается в математике в фигурные и квадратные скобки, рекомендую ознакомиться со статьей «Решение систем логарифмических и показательных неравенств». То есть в нашем случае:
Легко заметить, что первое неравенство выполняется при любом значении Следовательно, в составе системы на него вообще можно не обращать внимания. Ситуация несколько упрощается:
Способ №4. Графический. Строим в одной системе координат графики функции и Абсциссы точек их пересечения будут являться решениями уравнения. Метод менее точный, но более наглядный. Видно, что это все те же и
Соответствующие графики функций на одном координатном поле.
На этом список стандартных способов решения данного уравнения с модулем исчерпан. Придумайте свои нестандартные.
Простейшие уравнения с модулем
Пример 1. Решите уравнение:
Решение. Перепишем уравнение в виде:
Получается, что модуль выражения равен этому выражению, взятому с противоположным знаком. Такое возможно только в том случае, если данное выражение отрицательно или равно нулю:
Ответ:
Задача для самостоятельного решения №1. Решите уравнение
Показать ответ
Ответ:|
|
Решение. Исходное уравнение равносильно системе:
Обе части последних двух уравнений разделили на В данном случае В противном случае а это невозможно, поскольку
Окончательно, получаем:
Ответ:
Задача для самостоятельного решения №2. Решите уравнение:
Примечание. Для решения этого задания потребуется знание формулы суммы и разности синусов.
Показать ответ
Ответ:|
|
Решение. Перепишем уравнение в виде:
Сумма модулей равна сумме подмодульных выражений. Это возможно только в том случае, когда оба подмодульных выражения неотрицательны:
Ответ:
Задача для самостоятельного решения №3. Решите уравнение:
Показать ответ
Ответ:|
|
Решение. Сумма модулей равна модулю суммы подмодульных выражений. Это возможно только в том случае, когда оба подмодульных выражения одновременно либо неотрицательны, либо неположительны. То есть:
Ответ:
Задача для самостоятельного решения №4. Решите уравнение:
Показать ответ
Ответ:Простейшие неравенства с модулем
|
|
Решение. Исходное неравенство равносильно следующей системе неравенств:
Ответ:
Задача для самостоятельного решения №5. Решите неравенство:
Показать ответ
Ответ:|
|
Решение. Исходное неравенство равносильно следующей совокупности неравенств:
Ответ:
Задача для самостоятельного решения №6. Решите неравенство:
Показать ответ
Ответ: Пример 7. Решите неравенство:
Решение. Исходное неравенство равносильно следующему неравенству:
Ответ:
Задача для самостоятельного решения №8. Решите неравенство:
Показать ответ
Ответ:|
|
Решение. Исходное неравенство равносильно следующему неравенству:
Ответ:
Задача для самостоятельного решения №9. Решите неравенство:
Показать ответ
Ответ:Сергей ВалерьевичЧастный преподаватель по математике
yourtutor.info
Неравенства с модулем и их решение
Определение и формулы неравенств с модулем
ОПРЕДЕЛЕНИЕМодуль числа a равен числу a, если число положительное и -a, если оно отрицательное.
Можно записать следующим образом, что
Модуль числа — это расстояние от нуля до данного числа.
Если под модулем находится функция , то
1. Неравенство вида равносильно системе неравенств , при условии ; при — решений нет.
2. Неравенство вида равносильно совокупности неравенств , при условии, что . Если , то неравенство справедливо при всех допустимых значениях .
3. Неравенство равносильно двойному неравенству .
4. Неравенство равносильно совокупности неравенств
5. Неравенство вида выполняется тогда и только тогда, когда
Примеры решения неравенств с модулем
ПРИМЕР 2| Задание | Решить неравенство |
| Решение | Нулями подмодульных выражений являются значения и , которые разбивают числовую ось на три интервала.
Поскольку в результате преобразований получили верное неравенство, то решением будет любое действительное значение переменной: . Пересекаем с промежутком, на котором рассматриваем, и в результате получаем, что . Объединяя полученные интервалы в случаях 1-3, запишем решение заданного неравенства:
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com











