ГлавнаяРазноеПи математика

Число ПИ – математическая загадка. Пи математика


Число Пи. Интересно о математике

Математики, празднующие свой день рождения 14 марта, с некоторых пор получили дополнительный повод для торжества: именно этот день (который, исходя из американской традиции, записывается, как 3.14) объявлен Международным днем числа Пи — математической постоянной, выражающей соотношение длины окружности и длины ее диаметра: 3, 14159265358979323846 2643383279...

Проблема отношения длины окружности к ее диаметру возникла очень давно (по легенде, именно недостаточная точность этого числа стала причиной того, что Вавилонская башня так и не была построена) и долгое время древние ученые пользовались числом, равным трем. Однако первым, кто использовал средства математики для получения числа этого соотношения, был Архимед, который, занимаясь окружностями и многоугольниками, предположил, что «отношение любой окружности к ее диаметру меньше 3 1/7 и больше 3 10/71», получив, таким образом, число 3,1419...

Кстати, настоящие фанаты этого числа (а есть и такие!) отмечают свой праздник ровно в 1 час 59 минут и 26 секунд — по минимальному количеству цифр этого числа: 3,1415926...

Индийские ученые обнаружили несколько иное значение — 3,162..., а арабскому математику и астроному Масуду ал-Каши удалось вычислить 16 абсолютно точных цифр числа пи, благодаря чему был произведен переворот в астрономии. К слову, пресловутое соотношение длины окружности и ее диаметра получило всем известный современный символ пи с легкой руки английского математика У. Джонсона только в 1706 году. Это обозначение — своеобразная аббревиатура букв, с которых начинаются греческие слова «окружность» и «периметр». В XYII веке немецкий математик Лудольф Ван Цейлен, опираясь на метод Архимеда, в течение десяти лет пытался получить число пи до тридцать второго знака после запятой, и его упорство было вознаграждено тем, что число пи с этим количеством десятичных знаков называют «числом Лудольфа».

Благодаря этому легендарному числу был завершен один из самых длительных математических споров: получено доказательство невозможности решения самой известной классической задачи о квадратуре круга. Математики А. Лажандр и Ф.Линдеман получили подтверждение иррациональности (невозможности быть представленным в виде дроби, числитель которой — целое, а знаменатель — натуральное число) и трансцендентности (невычислимости с помощью простых уравнений) числа пи, из чего следует, что никому не под силу с помощью только лишь циркуля и линейки построить отрезок, длина которого была бы равна длине заданной окружности.

Усовершенствование математических методов позволило ученым позднего времени с еще большей точностью вычислить число пи. Эйлер, благодаря которому название этого числа стало общеупотребительным, «нашел» 153 верных десятичных знака, Шенкс — 527 и пр. Что говорить о современных математиках, которые с помощью компьютера легко вычислили сто миллиардов знаков после запятой! Японские ученые, получив число пи с точностью до 12411-триллионного знака, сразу же оказались в Книге рекордов Гиннеса: для того, чтобы установить этот рекорд им понадобился не только супермощный компьютер, но и 400 часов времени! Поскольку число пи — бесконечная математическая продолжительность, у каждого математика есть шанс побить японский рекорд.

Одной из особенностей числа пи является то, что числа в его десятичной части (следующей после запятой) не повторяются, что, по утверждению некоторых ученых, является свидетельством того, что число пи — это разумный (!) хаос, записанный цифрами. В результате этого любая последовательность цифр, которая только может возникнуть в нашей голове, может быть найдена в цифрах десятичной части числа пи.

Если кто-то думает, что вычисление бесконечных десятичных знаков этого числа — особое развлечение по-хорошему «сумасшедших» математиков, тот ошибается: от точности числа пи зависит точность не только земного, но и космического строительства.

Поделиться ссылкой

sitekid.ru

Пи (число) - это... Что такое Пи (число)?

Иррациональные числаγ - ζ(3) — √2 — √3 — √5 — φ — α — e — π — δ
Система счисления Оценка числа
Двоичная 11,00100100001111110110…
Десятичная 3,1415926535897932384626433832795…
Шестнадцатеричная 3,243F6A8885A308D31319…
Рациональное приближение 22⁄7, 223⁄71, 355⁄113,103993/33102, …

(перечислено в порядке увеличения точности)
Непрерывная дробь [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, … ]

(Эта непрерывная дробь не периодическая. Записана в линейной нотации)
Евклидова геометрия радиан = 180°

3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989

Первые 1000 знаков после запятой числа π[1] Если принять диаметр окружности за единицу, то длина окружности — это число «пи»

(произносится «пи») — математическая константа, выражающая отношение длины окружности к длине её диаметра.[2] Обозначается буквой греческого алфавита «пи». Старое название — лудольфово число.

Свойства

Трансцендентность и иррациональность

Соотношения

Известно много формул числа :

здесь простые числа

История

Символ константы

Впервые обозначением этого числа греческой буквой воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.

Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.

История числа шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров.

Геометрический период

То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским и древнегреческим геометрам. Самое раннее из известных приближений датируется 1900 годом до н. э.; это 25/8 (Вавилон) и 256/81 (Египет), оба значения отличаются от истинного не более, чем на 1 %. Ведийский текст «Шатапатха-брахмана» даёт как 339/108 ≈ 3,139.

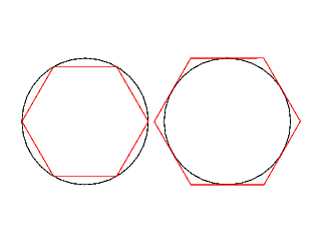
Алгоритм Лю Хуэя для вычисления

Архимед, возможно, первым предложил математический способ вычисления . Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку и предположил, что примерно равняется 22/7 ≈ 3,142857142857143.

Чжан Хэн во II веке уточнил значение числа , предложив два его эквивалента: 1) 92/29 ≈ 3,1724…; 2) ≈ 3,1622.

В Индии Ариабхата и Бхаскара использовали приближение 3,1416. Варахамихира в 6 веке пользуется в «Панча-сиддхантике» приближением .

Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм (англ. Liu Hui's π algorithm) для вычисления с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для по следующему принципу:

Позднее Лю Хуэй придумал быстрый метод вычисления и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.

В 480-х годах китайский математик Цзу Чунчжи продемонстрировал, что ≈ 355/113, и показал, что 3,1415926 < < 3,1415927, используя алгоритм Лю Хуэя применительно к 12288-угольнику. Это значение оставалось самым точным приближением числа в течение последующих 900 лет.

Классический период

До II тысячелетия было известно не более 10 цифр . Дальнейшие крупные достижения в изучении связаны с развитием математического анализа, в особенности с открытием рядов, позволяющих вычислить с любой точностью, суммируя подходящее количество членов ряда. В 1400-х годах Мадхава из Сангамаграма (англ. Madhava of Sangamagrama) нашёл первый из таких рядов:

Этот результат известен как ряд Мадхавы — Лейбница, или ряд Грегори — Лейбница (после того как он был заново обнаружен Джеймсом Грегори и Готфридом Лейбницем в XVII веке). Однако этот ряд сходится к очень медленно, что приводит к сложности вычисления многих цифр числа на практике — необходимо сложить около 4000 членов ряда, чтобы улучшить оценку Архимеда. Однако преобразованием этого ряда в

Мадхава смог вычислить как 3,14159265359, верно определив 11 цифр в записи числа. Этот рекорд был побит в 1424 году персидским математиком Джамшидом ал-Каши, который в своём труде под названием «Трактат об окружности» привёл 17 цифр числа , из которых 16 верные.

Первым крупным европейским вкладом со времён Архимеда был вклад голландского математика Людольфа ван Цейлена, затратившего десять лет на вычисление числа с 20-ю десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n = 60·229. Изложив свои результаты в сочинении «Об окружности» («Van den Circkel»), Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа . Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число иногда называли «лудольфовым числом», или «константой Лудольфа».

Примерно в это же время в Европе начали развиваться методы анализа и определения бесконечных рядов. Первым таким представлением была формула Виета:

,

найденная Франсуа Виетом в 1593 году. Другим известным результатом стала формула Валлиса:

,

выведенная Джоном Валлисом в 1655 году.

Аналогичные произведения:

Произведение, доказывающее родственную связь с числом Эйлера e :

В Новое время для вычисления используются аналитические методы, основанные на тождествах. Перечисленные выше формулы малопригодны для вычислительных целей, поскольку либо используют медленно сходящиеся ряды, либо требуют сложной операции извлечения квадратного корня.

Первую эффективную формулу нашёл в 1706 году Джон Мэчин (англ. John Machin)

Разложив арктангенс в ряд Тейлора

,

можно получить быстро сходящийся ряд, пригодный для вычисления числа с большой точностью.

Формулы такого типа, в настоящее время известные как формулы Мэчина (англ. Machin-like formula), использовались для установки нескольких последовательных рекордов и остались наилучшими из известных методов для быстрого вычисления в эпоху компьютеров. Выдающийся рекорд был поставлен феноменальным счетчиком Иоганном Дазе (англ. Johann Dase), который в 1844 году по распоряжению Гаусса применил формулу Мэчина для вычисления 200 цифр в уме. Наилучший результат к концу XIX века был получен англичанином Вильямом Шенксом (англ. William Shanks), у которого ушло 15 лет для того, чтобы вычислить 707 цифр, хотя из-за ошибки только первые 527 были верными. Чтобы избежать подобных ошибок, современные вычисления подобного рода проводятся дважды. Если результаты совпадают, то они с высокой вероятностью верные. Ошибку Шенкса обнаружил один из первых компьютеров в 1948 году; он же за несколько часов подсчитал 808 знаков .

Теоретические достижения в XVIII веке привели к постижению природы числа , чего нельзя было достичь лишь только с помощью одного численного вычисления. Иоганн Генрих Ламберт доказал иррациональность в 1761 году, а Адриен Мари Лежандр в 1774 году доказал иррациональность . В 1735 году была установлена связь между простыми числами и , когда Леонард Эйлер решил знаменитую Базельскую проблему (англ. Basel problem) — проблему нахождения точного значения

,

которое составляет . И Лежандр, и Эйлер предполагали, что может быть трансцендентным, что было в конечном итоге доказано в 1882 году Фердинандом фон Линдеманом.

Считается, что книга Уильяма Джонса «Новое введение в математику» c 1706 года первая ввела в использование греческую букву для обозначения этой константы, но эта запись стала особенно популярной после того, как Леонард Эйлер принял её в 1737 году. Он писал:

Существует множество других способов отыскания длин или площадей соответствующей кривой или плоской фигуры, что может существенно облегчить практику; например, в круге диаметр относится к длине окружности как 1 к

Эра компьютерных вычислений

Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр , которое заняло 70 часов. Ещё одна тысяча цифр была получена в последующие десятилетия, а отметка в миллион была пройдена в 1973 году. Такой прогресс имел место не только благодаря более быстрому аппаратному обеспечению, но и благодаря алгоритмам. Одним из самых значительных результатов было открытие в 1960 году быстрого преобразования Фурье, что позволило быстро осуществлять арифметические операции над очень большими числами.

В начале XX века индийский математик Сриниваса Рамануджан обнаружил множество новых формул для , некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины. Одна из этих формул — это ряд:

.

Братьями Чудновскими в 1987 году найдена похожая на неё:

,

которая даёт примерно по 14 цифр на каждый член ряда. Чудновские использовали эту формулу для того, чтобы установить несколько рекордов в вычислении в конце 1980-х, включая то, в результате которого в 1989 году было получено 1 011 196 691 цифр десятичного разложения. Эта формула используется в программах, вычисляющих на персональных компьютерах, в отличие от суперкомпьютеров, которые устанавливают современные рекорды.

В то время как последовательность обычно повышает точность на фиксированную величину с каждым следующим членом, существуют итеративные алгоритмы, которые на каждом шагу умножают количество правильных цифр, требуя, правда, высоких вычислительных затрат на каждом из таких шагов. Прорыв в этом отношении был сделан в 1975 году, когда Ричард Брент (англ. Richard P. Brent) и Юджин Саламин (англ. Eugene Salamin (mathematician)) независимо друг от друга открыли алгоритм Брента — Саламина (англ. Gauss–Legendre algorithm), который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков.[9] Алгоритм состоит из установки начальных значений

и итераций:

пока an и bn не станут достаточно близки. Тогда оценка даётся формулой

При использовании этой схемы 25 итераций достаточно для получения 45 миллионов десятичных знаков. Похожий алгоритм, увеличивающий на каждом шаге точность в четыре раза, был найден Джонатаном Боруэйном (англ. Jonathan Borwein) Питером Боруэйном (англ. Peter Borwein).[10] При помощи этих методов Ясумаса Канада и его группа, начиная с 1980 года, установили большинство рекордов вычисления вплоть до 206 158 430 000 знаков в 1999 году. В 2002 году Канада и его группа установили новый рекорд — 1 241 100 000 000 десятичных знаков. Хотя большинство предыдущих рекордов Канады были установлены при помощи алгоритма Брента — Саламина, вычисление 2002 года использовало две формулы типа мэчиновских, которые работали медленнее, но радикально снижали использование памяти. Вычисление было выполнено на суперкомпьютере Hitachi из 64 узлов с 1 терабайтом оперативной памяти, способном выполнять 2 триллиона операций в секунду.

Важным развитием недавнего времени стала формула Бэйли — Боруэйна — Плаффа (англ. Bailey–Borwein–Plouffe formula), открытая в 1997 году Саймоном Плаффом (англ. Simon Plouffe) и названная по авторам статьи, в которой она впервые была опубликована[11]. Эта формула,

примечательна тем, что она позволяет извлечь любую конкретную шестнадцатеричную или двоичную цифру числа без вычисления предыдущих.[11] С 1998 до 2000 года распределённый проект PiHex использовал видоизменённую формулу ББП Фабриса Беллара для вычисления квадриллионного бита числа , который оказался нулём.[12]

В 2006 году Саймон Плафф, используя PSLQ, нашёл ряд красивых формул.[13] Пусть q = eπ, тогда

и другие вида

где q = eπ, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:

для рационального p у которого знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.

В августе 2009 года учёные из японского университета Цукубо рассчитали последовательность из 2 576 980 377 524 десятичных разрядов.[14]

31 декабря 2009 года французский программист Фабрис Беллар на персональном компьютере рассчитал последовательность из 2 699 999 990 000 десятичных разрядов.[15]

2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо (яп.)русск. рассчитали последовательность с точностью в 5 триллионов цифр после запятой.[16][17]

19 октября 2011 года Александр Йи и Сигэру Кондо рассчитали последовательность с точностью в 10 триллионов цифр после запятой[18][19].

Рациональные приближения

Нерешённые проблемы

Метод иглы Бюффона

На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к при увеличении числа бросков до бесконечности.[26] Данный метод иглы базируется на теории вероятностей и лежит в основе метода Монте-Карло.[27]

Стихотворение для затвердевания в памяти 8-11 знаков числ π:

Чтобы нам не ошибаться,Надо правильно прочесть:Три, четырнадцать, пятнадцать,Девяносто два и шесть.

Надо только постаратьсяИ запомнить всё как есть:Три, четырнадцать, пятнадцать,Девяносто два и шесть.

Три, четырнадцать, пятнадцать,Девять, два, шесть, пять, три, пять.Чтоб наукой заниматься,Это каждый должен знать.

Можно просто постаратьсяИ почаще повторять:«Три, четырнадцать, пятнадцать,Девять, двадцать шесть и пять».

Запоминанию может помогать соблюдение стихотворного размера:

Три, четырнадцать, пятнадцать, девять два, шесть пять, три пятьВосемь девять, семь и девять, три два, три восемь, сорок шестьДва шесть четыре, три три восемь, три два семь девять, пять ноль дваВосемь восемь и четыре, девятнадцать, семь, один

Существуют стихи, в которых первые цифры числа π зашифрованы в виде количества букв в словах:

Это я знаю и помню прекрасно:Пи многие знаки мне лишни, напрасны.Доверимся знаньям громаднымТех, пи кто сосчитал, цифр армаду.

Раз у Коли и АриныРаспороли мы перины.Белый пух летал, кружился,Куражился, замирал,Ублажился,Нам же далГоловную боль старух.Ух, опасен пуха дух!

— Георгий Александров

Дополнительные факты

Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле

В культуре

См. также

Примечания

  1. ↑ PI
  2. ↑ Это определение пригодно только для евклидовой геометрии. В других геометриях отношение длины окружности к длине её диаметра может быть произвольным. Например, в геометрии Лобачевского это отношение меньше, чем .
  3. ↑ Lambert, Johann Heinrich. Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques, стр. 265–322.
  4. ↑ Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году.
  5. ↑ Weisstein, Eric W. Постоянная Гельфонда (англ.) на сайте Wolfram MathWorld.
  6. ↑ 1 2 Weisstein, Eric W. Иррациональное число (англ.) на сайте Wolfram MathWorld.
  7. ↑ Модулярные функции и вопросы трансцендентности
  8. ↑ Weisstein, Eric W. Pi Squared (англ.) на сайте Wolfram MathWorld.
  9. ↑ Brent, Richard (1975), Traub, J F, ed., "«Multiple-precision zero-finding methods and the complexity of elementary function evaluation»", Analytic Computational Complexity (New York: Academic Press): 151–176, <http://wwwmaths.anu.edu.au/~brent/pub/pub028.html>   (англ.)
  10. ↑ Jonathan M Borwein. Pi: A Source Book. — Springer, 2004. — ISBN 0387205713 (англ.)
  11. ↑ 1 2 David H. Bailey, Peter B. Borwein, Simon Plouffe. On the Rapid Computation of Various Polylogarithmic Constants // Mathematics of Computation. — 1997. — В. 218. — Т. 66. — С. 903—913. (англ.)
  12. ↑ Fabrice Bellard. A new formula to compute the nth binary digit of pi  (англ.). Архивировано из первоисточника 22 августа 2011. Проверено 11 января 2010.
  13. ↑ Simon Plouffe. Indentities inspired by Ramanujan’s Notebooks (part 2)  (англ.). Архивировано из первоисточника 22 августа 2011. Проверено 11 января 2010.
  14. ↑ Установлен новый рекорд точности вычисления числа π
  15. ↑ Pi Computation Record
  16. ↑ Число «Пи» рассчитано с рекордной точностью
  17. ↑ 1 2 5 Trillion Digits of Pi — New World Record (англ.)
  18. ↑ Определено 10 триллионов цифр десятичного разложения для π
  19. ↑ 1 2 Round 2… 10 Trillion Digits of Pi
  20. ↑ Weisstein, Eric W. Мера иррациональности (англ.) на сайте Wolfram MathWorld.
  21. ↑ Weisstein, Eric W. Pi (англ.) на сайте Wolfram MathWorld.
  22. ↑ en:Irrational number#Open questions
  23. ↑ Some unsolved problems in number theory
  24. ↑ Weisstein, Eric W. Трансцендентное число (англ.) на сайте Wolfram MathWorld.
  25. ↑ An introduction to irrationality and transcendence methods
  26. ↑ Обман или заблуждение? Квант № 5 1983 год
  27. ↑ Г. А. Гальперин. Биллиардная динамическая система для числа пи.
  28. ↑ Лудольфово число. Пи. Pi.
  29. ↑ Статья в Los Angeles Times «Желаете кусочек »? (название обыгрывает сходство в написании числа и слова pie (англ. пирог)) (англ.).
  30. ↑ Chinese student breaks Guiness record by reciting 67,890 digits of pi
  31. ↑ Interview with Mr. Chao Lu
  32. ↑ How can anyone remember 100,000 numbers? — The Japan Times, 17.12.2006.
  33. ↑ Pi World Ranking List
  34. ↑ The Indiana Pi Bill, 1897  (англ.)
  35. ↑ В. И. Арнольд любит приводить этот факт, см. например книгу Что такое математика (ps), стр. 9.

Литература

Ссылки

dik.academic.ru

Число «Пи»

14 мар 2012

14 марта математики отмечают один из самых необычных праздников — Международный день числа «Пи». Эта дата выбрана неслучайно: числовое выражение π (Пи) — 3,14 (3 месяц (март)  14 число). 

Впервые с этим необычным числом школьники сталкиваются уже в младших классах при изучении круга и окружности. Число π — математическая константа, которая выражает отношение длины окружности к длине ее диаметра. Т.е если взять окружность с диаметром равным единице, то длина окружности и будет равна числу «Пи». Число π имеет бесконечную математическую продолжительность, но в повседневных вычислениях используют упрощенное написание числа, оставляя только два знака после запятой, — 3,14.

В 1987 году этот день отмечался впервые. Физик Ларри Шоу из Сан-Франциско заметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 совпадает с числом π (π = 3,1415926…). Обычно  празднования начинаются в 1:59:26 дня (π = 3,1415926…).

История числа «Пи»

Предполагается, что история числа π начинается в Древнем Египте. Египетские математики определяли площадь круга диаметром Dкак (D-D/9)2. Из данной записи видно, что в то время число π приравнивали к дроби (16/9)2, или 256/81, т.е. π 3,160...

В VI в. до н.э. в Индии в религиозной книге джайнизма есть записи, свидетельствующие о том, что число π в то время принимали равным квадратному корню из 10, что даёт дробь 3,162...В III в. до  н.э.Архимед в своей небольшой работе "Измерение круга" обосновал три положения:

  1. Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
  2. Площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
  3. Отношение любой окружности к её диаметру меньше 3 1/7 и больше 3  10/71.

Последнее положение Архимед обосновал последовательным вычислением периметров правильных вписанных и описанных многоугольников при удвоении числа их сторон. По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3*10 / 71и 3*1/7, а это означает, что число «пи» равно  3,1419... Истинное значение этого отношения 3,1415922653...В V в. до н.э. китайский математик  Цзу Чунчжи нашёл  более точное значение этого числа: 3,1415927...Впервой половине XV в. астроном и математикал-Каши вычислил π с 16 десятичными знаками.

Спустя полтора столетия в Европе Ф.Виетнашёл число π только с 9 правильными десятичными знаками: он сделал 16 удвоений числа сторон многоугольников. Ф.Виетпервым заметил, что π можно отыскать, используя пределы некоторых рядов. Это открытие имело большое значение, оно позволило вычислить π с какой угодно точностью.

В 1706 г английский математик У.Джонсон ввёл обозначение отношения длины окружности к диаметру и обозначил его современным символом π первой буквой греческого слова periferia—окружность.

На протяжении длительного периода времени учёные всего мира пытались разгадать тайну этого загадочного числа.

В чем же сложность вычисления значения π ?

Число π является иррациональным: его невозможно выразить в виде дроби p/q, где p и q целые числа, данное число не может быть корнем алгебраического уравнения. Нельзя указать алгебраическое или дифференциальное уравнение, корнем которого будет π, поэтому данное число называется трансцендентным и вычисляется путём рассмотрения какого-либо процесса и уточняется за счет увеличения шагов рассматриваемого процесса. Множественные попытки просчитать максимальное количество знаков числа π привели к тому, что сегодня, благодаря современной вычислительной технике, можно рассчитать последовательность с точностью в 10 триллионов цифр после запятой.

Цифры десятичного представления числа π достаточно случайны. В десятичном разложении числа можно найти любую последовательность цифр. Предполагают, что в данном числе в зашифрованном виде есть все написанные и ненаписанные книги, любая информация, которую только можно представить, находится в числе π.

Можете сами попробовать разгадать тайну этого числа самостоятельно. Записать число «Пи» полностью, конечно не получится. Но самым любопытным предлагаю рассмотреть первые 1000 знаковчисла π  = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899   8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502   8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989

Запоминаем число «Пи»

В настоящее время с помощью вычислительной техники вычислено в десять триллионов знаков числа «Пи». Максимальное число цифр,  которое смог запомнить человек составляет сто тысяч.

Чтобы запомнить максимальное количество знаков числа «Пи», используют различные стихотворные «запоминалки», в которых слова с определённым количеством букв располагаются в такой же последовательности, как цифры в числе «Пи»: 3,1415926535897932384626433832795….  Для восстановления числа необходимо подсчитать число символов в каждом из слов и записать по порядку.

Вот и знаю я число, именуемое "Пи". Молодец! (7 цифр)

Вот и Миша и Анюта прибежалиПи узнать число они желали. (11 цифр)

Это я знаю и помню прекрасно:Пи многие знаки мне лишни, напрасны.Доверимся знаньям громаднымТех, пи кто сосчитал, цифр армаду. (21 цифра)

Раз у Коли и АриныРаспороли мы перины.Белый пух летал, кружился,Куражился, замирал,Ублажился,Нам же далГоловную боль старух.Ух, опасен пуха дух! (25 знаков)

Можно использовать рифмованные строки, которые помогают запомнить нужное число.

Чтобы нам не ошибиться,Нужно правильно прочесть:Три, четырнадцать, пятнадцать,Девяносто два и шесть

Если очень постараться,Можно сразу пи прочесть:Три, четырнадцать, пятнадцать,Девяносто два и шесть.

Три, четырнадцать, пятнадцать,Девять, два, шесть, пять, три, пять.Чтоб наукой заниматься,Это каждый должен знать.

Можно просто постаратьсяИ почаще повторять:«Три, четырнадцать, пятнадцать,Девять, двадцать шесть и пять».

Остались вопросы? Хотите знать больше о числе "Пи"?Чтобы получить помощь репетитора – зарегистрируйтесь.Первый урок – бесплатно!

Зарегистрироваться

www.tutoronline.ru

Число ПИ – математическая загадка

Загадочное число ПИ – математическая константа, являющаяся соотношением длины окружности и ее диаметра. На протяжении многих веков оно занимает умы математиков всего мира. Его считают даже мистическим, не поддающимся рациональному объяснению. Это особенно удивительно потому, что математика – самая точная из всех наук. Но она имеет лишь предположения насчет закономерностей в хаотической последовательности математической константы ПИ.

В 1794 году ученые доказали, что ПИ – бесконечное иррациональное число. Общепризнанным обозначением его является греческая буква "π". Загадка ПИ выходит далеко за пределы чистой математики, это число можно найти в формулах и явлениях, присущих другим наукам – астрономии, физике, теории относительности, генетике, статистике. Вездесущее число ПИ с его завораживающей последовательностью цифр, уходящей в бесконечность, для людей, неравнодушных к математике, является чем-то вроде произведения искусства.

Любители точных наук многих стран мира даже празднуют День ПИ. Конечно, этот праздник не является официальным. Его в 1987 придумал американский физик Ларри Шоу. Дата, выбранная для празднования, не случайна, она как бы зашифрована в самой константе. Зная, чему равно число ПИ, можно отгадать и дату праздника в его честь.

Из школьной программы нам известно как минимум 7 знаков после запятой, которые были заучены как стишок – «3-14-15-92 и 6». Третий месяц, 14 число… Вот и получается, что 14 марта точно в 1.59.26 вступает в права число ПИ. Празднующие любители математики произносят речи в честь константы, едят пирог с изображенной на нем греческой буквой "π" или первыми цифрами этого числа, играют в различные игры, решают головоломки – одним словом, развлекаются подобающим для математиков образом. Забавное совпадение – 14 марта появился на свет великий Альберт Энштейн, создатель теории относительности.

Фанаты числа ПИ соревнуются в попытках выучить как можно большее количество цифр константы. Рекорд пока принадлежит колумбийскому жителю Хайме Гарсия. Три дня потребовалось колумбийцу на озвучивание 150 тысяч знаков. Рекорд человека-компьютера подтвержден профессорами математики и занесен в книгу Гиннеса.

Число ПИ полностью воспроизвести невозможно, оно бесконечно. В нем нет ни единой циклической последовательности, и, по мнению математиков, таковая никогда не обнаружится, сколько бы не вычислили еще знаков.

Американский математик Дэвид Бэйли со своими канадскими коллегами создал специальную компьютерную программу, вычисления по которой показали, что последовательность цифр числа ПИ действительно случайна, словно иллюстрирующая теорию хаоса.

На протяжении многовековой истории числа ПИ ведется своеобразная погоня за количеством его цифр. Последние данные удалось вывести японским ученым из университета Цукуба – точность их вычислений составляет больше 2,5 триллионов десятичных знаков. Расчеты производились на суперкомпьютере, оборудованном 640 четырехъядерными процессорами, а заняли 73 с половиной часа.

В заключение хочется привести отрывок из детского стихотворения Сергея Боброва. Как вы думаете, что здесь зашифровано?

«22 совы скучали на больших сухих суках.

22 совы мечтали

о семи больших мышах»

(При делении 22 на 7 получается… число ПИ).

fb.ru

Что особенного в числе Пи? Отвечает математик | Образование | Общество

Сегодня день рождения числа Пи, который, по инициативе американских математиков, отмечается 14 марта в 1 час и 59 минут пополудни. Связано это с более точным значением числа Пи: все мы привыкли считать эту константу как 3,14, но число можно продолжить так: 3, 14159... Переводя это в календарную дату, получаем 03.14, 1:59.

Фото: АиФ/ Надежда Уварова

Профессор кафедры математического и функционального анализа Южно-Уральского государственного университета Владимир Заляпин говорит, что «днём числа Пи» всё же следует считать 22 июля, потому что в европейском формате дат этот день записывается как 22/7, а значение этой дроби приблизительно равно значению Пи.

«История числа, дающего отношение длины окружности к диаметру окружности, уходит в далёкую древность, — рассказывает Заляпин. — Уже шумеры и вавилоняне знали, что это это отношение не зависит от диаметра окружности и является постоянным. Одно из первых упоминаний о числе Пи можно встретить в текстах египетского писца Ахмеса (около 1650 года до н. э.). Древние греки, много позаимствовавшие у египтян, внесли свой вклад в развитие этой загадочной величины. По легенде, Архимед был настолько увлечён расчётами, что не заметил, как римские солдаты взяли его родной город Сиракузы. Когда римский солдат подошёл к нему, Архимед закричал по-гречески: «Не трогай моих кругов!». В ответ солдат заколол его мечом.

Платон получил довольно точное значение числа Пи для своего времени — 3,146. Лудольф ванн Цейлен провёл большую часть своей жизни над расчётами первых 36 цифр после запятой числа Пи, и они были выгравированы на его надгробной плите после смерти».

Иррациональное и ненормальное

По словам профессора, во все времена погоня за вычислением новых десятичных знаков обуславливалась желанием получить точное значение этого числа. Предполагалось, что число Пи рациональное и, следовательно, может быть выражено простой дробью. А это в корне неверно!

Число Пи популярно ещё и потому, что оно — мистическое. С древних времён существовала религия почитателей константы. Помимо традиционного значения Пи — математической константы (3,1415...), выражающей отношение длины окружности к её диаметру, есть масса других значений цифры. Любопытны такие факты. В процессе измерений размеров Великой пирамиды в Гизе оказалось, что она имеет такое же соотношение высоты к периметру своего основания, как радиус окружности к её длине, то есть ½ Пи.

Если рассчитать длину экватора Земли с использованием числа Пи с точностью до девятого знака, ошибка в расчётах составит всего около 6 мм. Тридцати девяти знаков после запятой в числе Пи достаточно для вычисления длины окружности, опоясывающей известные космические объекты во Вселенной, с погрешностью не большей, чем радиус атома водорода!

Изучением Пи занимается в том числе и математический анализ. Фото: АиФ/ Надежда Уварова

Хаос в цифрах

По словам профессора математики, в 1767 году Ламберт установил иррациональность числа Пи, то есть невозможность представить его отношением двух целых. Это означает, что последовательность десятичных знаков числа Пи — это хаос, овеществлённый в цифрах. Иными словами, в «хвосте» десятичных знаков содержится любое число, любая последовательность чисел, любые тексты, которые были, есть и будут, да только извлечь эту информацию не представляется возможным!

«Точное значение числа Пи узнать невозможно, — продолжает Владимир Ильич. — Но попытки эти не оставляются. В 1991 году Чудновские добились новых 2260000000 десятичных знаков константы, а в 1994 году — 4044000000. После этого количество верных знаков числа Пи нарастало лавинообразно».

Мировой рекорд по запоминанию числа Пи у китайца Лю Чао, который сумел запомнить 67890 знаков после запятой без ошибки и воспроизвести их в течение 24 часов и 4 минут.

О «золотом сечении»

Кстати, связь между «пи» и другой удивительной величиной — золотым сечением — на самом деле так и не доказана. Люди давно заметили, что «золотая» пропорция — она же число Фи — и число Пи, делённое на два, различаются между собой меньше, чем на 3% (1,61803398... и 1,57079632...). Однако для математики эти три процента — разница слишком существенная, чтобы считать эти значения тождественными. Точно так же можно сказать, что число Пи и число Фи являются родственниками ещё одной известной постоянной — числа Эйлера, так как корень из него близок к половине числа Пи. Одна вторая Пи — 1, 5708, Фи — 1,6180, корень из Е — 1, 6487. 

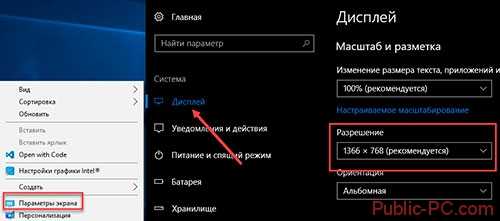
Это — лишь часть значения Пи. Фото: Скриншот

День рождения Пи

В Южно-Уральском государственном университете день рождения константы отмечают все преподаватели и студенты-математики. Так было всегда — нельзя сказать, что интерес появился лишь в последние годы. Число 3,14 приветствуют даже специальным праздничным концертом!

Смотрите также:

www.aif.ru

Пи (число) | Наука | FANDOM powered by Wikia

Символ константы

Список чисел Система счисления Оценка числа $ \pi $ Двоичная 11,00100100001111111... Десятичная 3,141592653589793238462... Шестнадцатеричная 3,243F6A8885A308D31319... Рациональное приближение 22⁄7,223⁄71, 355⁄113 …

(в порядке увеличения точности)

Цепная дробь [3; 7, 15, 1, 1, 1, 1, 2, 1,... ]

(Цепная дробь не периодическая. Дана в линейной нотации)

Евклидова геометрия $ \pi $ радиан = 180°
Иррациональные числа ζ(3) (англ.) — √2 (англ.) — √3 (англ.) — √5 (англ.) — φ — α — e — π — δ

Пи (число) — $ \pi~ $ (произносится «пи») — математическая константа, выражающая отношение длины окружности к длине её диаметра.[1] Обозначается буквой греческого алфавита «пи».

    $ \pi $ — иррациональное число, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. $ \pi $ также не может представлено как конечная последовательность алгебраических операций над целыми числами (возведение в степень, извлечение корня, суммирование и т. д.). Править

    $ \pi $ — трансцендентное число, это означает, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами; доказательство этого Ф. Линдеманом было крупным достижением математики XIX столетия. На всём протяжении истории математики было множество попыток более точно определить и понять природу числа $ \pi $; привлекательность этого числа перекинулась даже на нематематическую культуру. Править

    === Впервые обозначением этого числа греческой буквой $ \pi~ $ воспользовался британский математик Джонс (1706), а общепринятым оно стало после работ Леонарда Эйлера в 1737. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр. ===

    История Править

    Если принять диаметр окружности за единицу, то длина окружности — это число «пи». Править

    История числа $ \pi $ шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого $ \pi $ изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров. Править

    ===

    ===

    Геометрический период Править

    То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским и древнегреческим геометрам. Самое раннее из известных приближений датируется 1900 годом до н. э.; это 25/8 (Вавилон) и 256/81 (Египет), оба значения отличаются от истинного не более, чем на 1 %. Индийский текст «Шатапатха Брахмана» даёт $ \pi $ как 339/108 ≈ 3,139. По-видимому, в еврейской Библии, в третьей книге Царств, предполагается, что $ \pi $ = 3, что является гораздо более худшей оценкой, чем имевшиеся на момент написания (600 год до н. э.). Править

    Править

    Алгоритм Лю Хуэя вычисления $ \pi $ Править

    Архимед, возможно, первым предложил математический способ вычисления $ \pi $. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку $ 3+\frac{10}{71} < \pi <3+\frac{1}{7} $. Править

    В Индии Арьябхата и Бхаскара использовали приближение 3,1416. Брахмагупта предложил в качестве приближения $ \sqrt{10} $.

    Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм (англ. Liu Hui's π algorithm) для вычисления $ \pi $ с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для $ \pi $ по следующему принципу:

    $ \pi\approx A_{3072} = {3 \cdot 2^8\cdot \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+1}}}}}}}}}} \approx 3,14159. $

    Позднее Лю Хуэй придумал быстрый метод вычисления $ \pi $ и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.

    В 480-х годах китайский математик Цзу Чунчжи (англ. Zu Chongzhi) продемонстрировал, что $ \pi $ ≈ 355/113, и показал, что 3,1415926 < $ \pi $ < 3,1415927, используя алгоритм Лю Хуэя применительно к 12288-угольнику. Это значение оставалось самым точным приближением числа $ \pi $ в течение последующих 900 лет.

    Классический период Править

    До 2-го тысячелетия было известно не более 10 цифр $ \pi $. Дальнейшие крупные достижения в изучении $ \pi $ связаны с развитием математического анализа, в особенности с открытием рядов, позволяющих вычислить $ \pi $ с любой точностью, суммируя подходящее количество членов ряда. В 1400-х годах Мадхава из Сангамаграма (англ. Madhava of Sangamagrama) нашёл первый из таких рядов:

    $ {\pi} = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \cdots\! $

    Этот результат известен как ряд Мадхавы-Лейбница (англ. Leibniz formula for pi) или ряд Грегори-Лейбница (после того как он был заново обнаружен Джеймсом Грегори и Готфридом Лейбницем в XVII веке). К сожалению, этот ряд сходится к $ \pi $ очень медленно, что приводит к сложности вычисления многих цифр числа на практике — необходимо сложить около 4000 членов ряда, чтобы улучшить оценку Архимеда. Однако преобразованием этого ряда в

    $ \pi = \sqrt{12} \, \left(1-\frac{1}{3 \cdot 3} + \frac{1}{5 \cdot 3^2} - \frac{1}{7 \cdot 3^3} + \cdots\right)\! $

    Мадхава (англ. Madhava of Sangamagrama) смог вычислить $ \pi $ как 3,14159265359, верно определив 11 цифр в записи числа. Этот рекорд был побит в 1424 году персидским математиком Джамшидом ал-Каши, который в своём труде под названием «Трактат об окружности» привёл 17 цифр числа $ \pi $, из которых 16 верные.

    Первым крупным европейским вкладом со времён Архимеда был вклад голландского математика Лудольфа ван Цейлена (1540—1610), затратившего десять лет на вычисление числа $ \pi $ с 20-ю десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n = 60·229. Изложив свои результаты в сочинении «Об окружности» («Van den Circkel»), Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа $ \pi $. Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число $ \pi $ иногда называли «лудольфовым числом», или «константой Лудольфа».

    Примерно в это же время в Европе начали развиваться методы анализа и определения бесконечных рядов. Первым таким представлением была формула Виета (англ. Viète's formula)

    $ \frac2\pi = \frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \cdots\! $

    найденная Франсуа Виетом в 1593 году. Другим известным результатом стала Формула Валлиса (англ. Wallis product),

    $ \frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots\! $

    выведенная Джоном Валлисом в 1655 году.

    В Новое время для вычисления $ \pi $ используются аналитические методы, основанные на тождествах. Перечисленные выше формулы малопригодны для вычислительных целей, поскольку либо используют медленно сходящиеся ряды, либо требуют сложной операции извлечения квадратного корня.

    Первую эффективную формулу нашёл в 1706 году Джон Мэчин (John Machin):

    $ \frac{\pi}{4} = 4\,\mathrm{arctg}\frac{1}{5} - \mathrm{arctg}\frac{1}{239} $

    Разложив арктангенс в ряд Тейлора

    $ \arctan \, x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots\! $,

    можно получить быстро сходящийся ряд, пригодный для вычисления числа $ \pi $ с большой точностью. Эйлер, автор обозначения $ \pi $, получил 153 верных знака.

    Формулы такого типа, в настоящее время известные как Формулы Мэчина (англ. Machin-like formula), использовались для установки нескольких последовательных рекордов и остались наилучшими из известных методов для быстрого вычисления $ \pi $ в эпоху компьютеров. Выдающийся рекорд был поставлен феноменальным счетчиком Иоганном Захариусом Дазе (англ. Zacharias Dase), который в 1844 году по распоряжению Гаусса применил формулу Мэчина для вычисления 200 цифр $ \pi $ в уме. Наилучший результат к концу XIX века был получен англичанином Вильямом Шенксом (англ. William Shanks), у которого ушло 15 лет для того, чтобы вычислить 707 цифр, хотя из-за ошибки только первые 527 были верными. (Чтобы избежать подобных ошибок, современные вычисления подобного рода проводятся дважды. Если результаты совпадают, то они с высокой вероятностью верные.) Ошибку Шенкса обнаружил один из первых компьютеров в 1948 году; он же за несколько часов подсчитал 808 знаков $ \pi $.

    Теоретические достижения в XVIII веке привели к постижению природы числа $ \pi $, чего нельзя было достичь лишь только с помощью одного численного вычисления. Иоганн Генрих Ламберт доказал иррациональность $ \pi $ в 1761 году, а Адриен Мари Лежандр в 1774 году доказал иррациональность $ \pi^2 $. В 1735 году была установлена связь между простыми числами и $ \pi $, когда Леонард Эйлер решил знаменитую Базельскую проблему (англ. Basel problem) — проблему нахождения точного значения

    $ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots\! $,

    которое составляет $ \frac{\pi^2}{6} $. И Лежандр, и Эйлер предполагали, что $ \pi $ может быть трансцендентным, что было в конечном итоге доказано в 1882 году Фердинандом фон Линдеманом.

    Считается, что книга Уильяма Джонса Новое введение в математику c 1706 года первая ввела в использование греческую букву $ \pi $ для обозначения этой константы, но эта запись стала особенно популярной после того, как Леонард Эйлер принял её в 1737 году. Он писал:

    Существует множество других способов отыскания длин или площадей соответствующей кривой или плоской фигуры, что может существенно облегчить практику; например, в круге диаметр относится к длине окружности как 1 к $ (\frac{16}{5}-\frac{4}{239})-\frac{1}{3} \cdot (\frac{16}{5^3}-\frac{4}{239^3})+\cdots = 3.14159 \cdots = \pi $

    Эра компьютерных вычислений Править

    Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и др. использовали в 1949 году ЭНИАК для вычисления 2037 цифр $ \pi $, которое заняло 70 часов. Ещё одна тысяча цифр была получена в последующие десятилетия, а отметка в миллион была пройдена в 1973 году. Такой прогресс имел место не только благодаря более быстрому аппаратному обеспечению, но и благодаря алгоритмам. Одним из самых значительных результатов было открытие в 1960-м году быстрого преобразования Фурье (БПФ), что позволило быстро осуществлять арифметические операции над очень большими числами.

    В начале 20-го столетия индийский математик Сриниваса Рамануджан обнаружил множество новых формул для $ \pi $, некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины. Одна из этих формул — это ряд

    $ \frac{1}{\pi} = \frac{2 \sqrt 2}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}\! $,

    и похожая на неё, найденная братьями Чудновскими (англ.) в 1987,

    $ \frac{426880 \sqrt{10005}}{\pi} = \sum_{k=0}^\infty \frac{(6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 (-640320)^{3k}}\! $,

    который вычисляет по 14 цифр за ход. Чудновские использовали эту формулу для того, чтобы установить несколько рекордов в вычислении $ \pi $ в конце 1980-х, включая то, в результате которого было получено более миллиарда (1,011,196,691) цифр десятичного разложения (1989 год). Эта формула используется в программах, вычисляющих $ \pi $ на персональных компьютерах, в отличие от суперкомпьютеров, которые устанавливают современные рекорды.

    В то время как последовательность обычно повышает точность на фиксированную величину с каждым следующим членом, существуют итеративные алгоритмы, которые на каждом шагу умножают количество правильных цифр, требуя, правда, высоких вычислительных затрат на каждом из таких шагов. Прорыв в этом отношении был сделан в 1975 году, когда Ричард Брент (англ.) и Юджин Саламин (англ.) независимо друг от друга открыли алгоритм Брента — Саламина (англ.), который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков.[2] Алгоритм состоит из установки начальных значений

    $ a_0 = 1 \quad \quad \quad b_0 = \frac{1}{\sqrt 2} \quad \quad \quad t_0 = \frac{1}{4} \quad \quad \quad p_0 = 1\! $

    и итераций:

    $ a_{n+1} = \frac{a_n+b_n}{2} \quad \quad \quad b_{n+1} = \sqrt{a_n b_n}\! $ $ t_{n+1} = t_n - p_n (a_n-a_{n+1})^2 \quad \quad \quad p_{n+1} = 2 p_n\! $

    пока an и bn не станут достаточно близки. Тогда оценка $ \pi $ даётся формулой

    $ \pi \approx \frac{(a_n + b_n)^2}{4 t_n}.\! $

    При использовании этой схемы 25 итераций достаточно для получения 45 миллионов десятичных знаков. Похожий алгоритм, увеличивающий на каждом шаге точность в четыре раза, был найден Джонатаном Боруэйном (Jonathan Borwein) и Питером Боруэйном (en:Peter Borwein).[3] При помощи этих методов Ясумаса Канада (en:Yasumasa Kanada) и его группа, начиная с 1980 года, установили большинство рекордов вычисления $ \pi $ вплоть до 206,158,430,000 знаков в 1999. Текущий рекорд — 1 241 100 000 000 десятичных знаков, установлен Канадой и его группой в 2002 году. Хотя большинство предыдущих рекордов Канады были установлены при помощи алгоритма Брента-Саламина, вычисление 2002 года использовало две формулы типа мэчиновских, которые работали медленнее, но радикально снижали использование памяти. Вычисление было выполнено на суперкомпьютере Хитачи из 64 узлов с 1 терабайтом оперативной памяти, способном выполнять 2 триллиона операций в секунду.

    Важным развитием недавнего времени стала формула Бэйли—Боруэйна—Плаффа (en:Bailey–Borwein–Plouffe formula) (формула ББП), открытая Саймоном Плаффом (en:Simon Plouffe) и названная по авторам статьи, в которой она впервые была опубликована — David H. Bailey, Peter Borwein, and Plouffe.[4] Эта формула,

    $ \pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right), $

    примечательна тем, что она позволяет извлечь любую конкретную шестнадцатеричную или двоичную цифру числа $ \pi $ без вычисления предыдущих.[4] С 1998 до 2000 года распределённый проект PiHex использовал видоизменённую формулу ББП Фабриса Беллара для вычисления квадриллионного (1 000 000 000 000 000-го) бита числа $ \pi $, который оказался нулём.[5]

    В 2006 году Саймон Плафф, используя en:integer relation algorithm PSLQ, нашёл ряд красивых формул.[6] Пусть q = eπ, тогда

    $ \frac{\pi}{24} = \sum_{n=1}^\infty \frac{1}{n} \left(\frac{3}{q^n-1} - \frac{4}{q^{2n}-1} + \frac{1}{q^{4n}-1}\right) $ $ \frac{\pi^3}{180} = \sum_{n=1}^\infty \frac{1}{n^3} \left(\frac{4}{q^n-1} - \frac{5}{q^{2n}-1} + \frac{1}{q^{4n}-1}\right) $

    и другие вида

    $ \pi^k = \sum_{n=1}^\infty \frac{1}{n^k} \left(\frac{a}{q^n-1} + \frac{b}{q^{2n}-1} + \frac{c}{q^{4n}-1}\right) $

    где q = eπ, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:

    $ p\pi^k = \sum_{n=1}^\infty \frac{1}{n^k} \left(\frac{2^{k-1}}{q^n-1} - \frac{2^{k-1}+1}{q^{2n}-1} + \frac{1}{q^{4n}-1}\right) $

    для рационального p у которго знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.

    В 2009 году учёные из Университата Цукубо (Япония) рассчитали последовательность из 2 576 980 377 524 десятичных разрядов.[7]

    • $ \frac{22}{7} $ (Архимед),
    • $ \frac{377}{120} $ (дана в книге индийского мыслителя и астронома Арьябхаты в V веке н. э.),
    • $ \frac{355}{113} $ (оценка приписывается современнику Арьябхаты древнекитайскому астроному Цзу Чун-цжи).
    • 510 знаков после запятой: π ≈ 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362…
    • Двести миллиардов знаков после запятой (2000 ZIP архивов, средний размер файла около 57 мегабайт)

    Соотношения Править

    Известно много формул с числом $ \pi $:

    $ \frac2\pi= \frac{\sqrt{2}}2\cdot \frac{\sqrt{2+\sqrt2}}2\cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \ldots $ $ \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2} $ $ \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4} $ $ e^{i \pi} + 1 = 0\; $ $ \int\limits_{-\infty}^{+\infty}\ e^{-x^2}{dx} = \sqrt{\pi} $ $ \int\limits_{-\infty }^{+\infty }{\frac{\sin x}{x}dx}=\pi $

    Трансцендентность и иррациональность Править

    Нерешённые проблемы Править

    • Неизвестно, являются ли числа $ \pi $ и $ e $ алгебраически независимыми.
    • Неизвестно, являются ли числа $ \pi + e $, $ \pi - e $, $ \pi e $, $ \pi / e $, $ \pi ^ e $, $ \pi ^ \pi $, $ e ^ e $ трансцендентными.
    • До сих пор ничего не известно о нормальности числа $ \pi $; неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа $ \pi $ бесконечное количество раз.

    История вычисления Править

    В 1997 году Дэйвид Х. Бэйли, Питер Боруэйн и Саймон Плуфф открыли способ быстрого вычисления произвольной двоичной цифры числа $ \pi $ без вычисления предыдущих цифр, основанный на формуле

    $ \pi = \sum_{i=0}^{\infty}\frac{1}{16^i}\left(\frac{4}{8i+1}-\frac{2}{8i+4}-\frac{1}{8i+5}-\frac{1}{8i+6}\right) $

    Метод иглы Бюффона Править

    На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к $ \frac2\pi $ при увеличении числа бросков до бесконечности. Данный метод иглы базируется на теории вероятностей и лежит в основе метода Монте-Карло.[9]

    Дополнительные факты Править

    Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле

    • Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа $ \pi $.
    • Ещё одной датой, связанной с числом $ \pi $, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа $ \pi $.
    • 17 июня 2009 года украинский нейрохирург, доктор медицинских наук, профессор Андрей Слюсарчук установил мировой рекорд, запомнив 30 миллионов знаков числа Пи, которые были напечатаны в 20 томах текста.[10] С установлением нового рекорда Андрея Слюсарчука официально поздравил Президент Украины Виктор Андреевич Ющенко.[11][12] Поскольку устное перечисление 30 млн цифр $ \pi $ со скоростью одна цифра в секунду заняло бы почти год (347 дней) при непрерывном перечислении 24 часа в сутки, 7 дней в неделю, то был применён следующий подход для проверки рекорда: во время демонстраций г. Слюсарчука просят назвать произвольно выбранные проверяющими последовательности цифр числа Пи, расположенные на произвольно выбранных местах произвольных страниц 20-томной распечатки, группированной в упорядоченные таблицы. Он многократно успешно проходит этот тест. Свидетелями демонстраций были уважаемые учёные, доктора и кандидаты наук, заведующие кафедрами Институтов и Университетов. Книга рекордов Украины перечисляет членов комиссии, участвовавших в демонстрациях. Приведены их научные звания и занимаемые должности. Уникальная память Андрея Слюсарчука основана на эйдетическом восприятии информации.
    • По данным Книги рекордов Украины, в 2006 году Андрей Слюсарчук установил предыдущий мировой рекорд, запомнив 1 миллион знаков числа Пи.[13]
    • Предыдущий мировой рекорд по запоминанию знаков числа $ \pi $ принадлежит японцу Акире Харагути (Akira Haraguchi). Он запомнил число $ \pi $ до 100-тысячного знака после запятой. Ему понадобилось почти 16 часов, чтобы назвать всё число целиком. (на запоминание ушло 10 лет)[14]
    • В штате Индиана (США) в 1897 году был выпущен билль (см.: en:Indiana Pi Bill), законодательно устанавливающий значение числа Пи равным 3,2.[15] Данный билль не стал законом благодаря своевременному вмешательству профессора Университета Пердью (англ. Purdue University), присутствовавшего в законодательном собрании штата во время рассмотрения данного закона.
    • «число Пи для гренландских китов равно 3.14» написано в «Справочнике китобоя» 60-х годов выпуска.[16]
    • Существует художественный фильм, названный в честь числа Пи.
    1. ↑ Это определение пригодно только для евклидовой геометрии. В других геометриях отношение длины окружности к длине её диаметра может быть произвольным. Например, в геометрии Лобачевского это отношение меньше, чем $ \pi~ $.
    2. ↑ Brent, Richard (1975), Traub, J F, ed., "Multiple-precision zero-finding methods and the complexity of elementary function evaluation", Analytic Computational Complexity (New York: Academic Press): 151–176, http://wwwmaths.anu.edu.au/~brent/pub/pub028.html, retrieved 2007-09-08 
    3. ↑ Borwein, Jonathan M; Borwein, Peter, Berggren, Lennart (2004). Pi: A Source Book. Springer. ISBN 0387205713. 
    4. ↑ 4,04,1Bailey, David H., Borwein, Peter B., and Plouffe, Simon (April 1997). "On the Rapid Computation of Various Polylogarithmic Constants" (PDF). Mathematics of Computation 66 (218): 903–913. doi:10.1090/S0025-5718-97-00856-9.  
    5. ↑ Bellard, Fabrice A new formula to compute the nth binary digit of pi. Проверено 27 октября 2007.
    6. ↑ Plouffe, Simon Indentities inspired by Ramanujan's Notebooks (part 2). Проверено 10 апреля 2009.
    7. ↑ Установлен новый рекорд точности вычисления числа π
    8. ↑ Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году
    9. ↑ Г. А. Гальперин. Биллиардная динамическая система для числа пи.
    10. ↑ Профессор Андрей Слюсарчук установил мировой рекорд по возможностям человеческой памяти http://www.mk.ru/health/303812.html?phrase_id=1446233
    11. ↑ Президент поздравил профессора Андрея Слюсарчука с установлением нового мирового рекорда по запоминанию и воспроизведению человеком сверхбольшого объема информации http://www.president.gov.ua/ru/news/14234.html
    12. ↑ Ющенко привітав Слюсарчука зі світовим рекордом із запам’ятовування надвеликого обсягу інформації http://news.liga.net/ukr/news/NU094415.html
    13. ↑ Книга рекордов Украины http://www.book.adamant.ua/akt/2slysar4uk/1.htm
    14. ↑ Japanese man recites pi from memory to 100,000 decimal places, claims world record. The Associated Press (04/10/06). Проверено 22 сентября 2008.
    15. ↑ The Indiana Pi Bill, 1897
    16. ↑ В. И. Арнольд любит приводить этот факт, см. например здесь (ps)

    ru.science.wikia.com

    Число пи | Математика, которая мне нравится

    Лейб Штейнгарц,доктор педагогики.Иерусалим, Израиль[email protected]

    Топ причин, почему лучше, чем .

    Мы, участники международной конференции “Число Пи – самое лучшее”, не можем без равнодушия наблюдать за тем, как некоторые, так называемые любители числа , утверждают, что число лучше, чем число Пи.

    Мы с этим утверждением категорически не согласны.

    Поэтому формулируем свои 10 причин, которые, очевидным образом, опровергают то, что сформулировали любители числа .

    1) Число по-английски произносится ПАЙ, что означает пирог. Мало того, слово ПИРОГ по-русски начинается с числа ПИ.

    2) С числа ПИ начинается имя великого древнегреческого геометра ПИФАГОРА, который исследовал число ПИ.Правда, с числа начинается имя другого великого древнегреческого математика Евклида. Но он никогда не использовал в своих научных работах число .

    3) С числа ПИ начинаются такие всемирно известные достопримечательности, как:ПИзанская башня.ПИрамиды.ПИтер.

    4) Число ПИ можно изобразить при помощи трех спичек, а для изображения числа спичек понадобится больше.

    5) и достаточно скверные числа, тогда как , а .

    6) Вам вовсе не нужно знать греческий язык, чтобы использовать . Точно также, как и не нужно знать, например, еврейский язык, чтобы использовать в теории множеств букву .

    7) очень часто используется не только в “детской геометрии”, но и в математическом анализе тоже.Кроме того, в математическом анализе число иногда просто подразумевается, но не пишется (в случае функции ).

    А число пишется ВСЕГДА !

    8 ) , тогда как  

    9) — это число Эйлера, а число принадлежит всем народам и каждому человеку в отдельности!.

    10) Ребенок, как правило, гораздо раньше произносит “ПИ – ПИ”, чем “е – е”.

    hijos.ru