ГлавнаяРазноеПроекции вектора определение

Проекция вектора на ось. Проекция вектора на вектор. Проекции вектора определение


Проекция вектора на вектор, формула и примеры

Определение и формула проекции вектора на вектор

Проекцией вектора на ось называется число, которое равно величине отрезка , принадлежащего указанной оси, где точки и – проекции точек и на рассматриваемую ось соответственно (рис. 1).

ОПРЕДЕЛЕНИЕ Проекцией вектора на направление вектора , называется число, которое равно величине проекции вектора на ось , проходящую через второй вектор (рис. 2).

Проекция вектора на направление вектора равна скалярному произведению этих векторов, деленному на длину вектора :

   

Примеры нахождения проекции вектора на вектор

ПРИМЕР
Задание Найти проекцию вектора на вектор
Решение Вычислим скалярное произведение заданных векторов. Оно равно сумме произведений соответствующих координат векторов-сомножителей

   

Модуль вектора равен корню квадратному из суммы квадратов координат, то есть

   

Тогда искомая проекция

   

Ответ
ПРИМЕР
Задание Найти модуль вектора , если известно, что проекция вектора на него равна 2, а скалярное произведение этих векторов
Решение Согласно формуле имеем, что

   

Тогда

   

Ответ

ru.solverbook.com

Проекция вектора на ось, формула и примеры

Определение и формула проекции вектора на ось

Под осью понимается прямая, для которой указано направление.

Чтобы построить проекцию вектора на ось , нужно из точек и (начало и конец вектора соответственно) опустить перпендикуляры на направленную прямую , основания этих перпендикуляров будут началом и концом искомой проекции (рис. 1).

Числовой характеристикой проекции вектора на ось является числовая проекция этого вектора на данную ось – число, которое равно произведению длины данного вектора на косинус угла между этим вектором и вектором, определяющим направление оси.

Если направление оси определяется вектором , то числовая проекция вектора на эту ось обозначается как , причем

   

Примеры нахождения проекции вектора на ось

Из определения скалярного произведения двух векторов и :

   

получаем, что

   

В результате формула (1) принимает вид:

   

То есть числовой проекцией вектора на ось, направление которой совпадает с направлением вектора , есть отношение скалярного произведения векторов и к модулю вектора :

   

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Проекция вектора.

Навигация по странице:

Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l. (рис. 1).

рис. 1

Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.

Формула вычисления проекции вектора на вектор

Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:

Примеры задач на проекцию вектора

Примеры вычисления проекции вектора для плоских задач

Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.

Решение:

Найдем скалярное произведение этих векторов

a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11

Найдем модуль вектора b

|b| = √32 + 42 = √9 + 16 = √25 = 5

Найдем проекцию вектора a на вектор b

Пр ba = a · b  = 11 = 2.2
|b|5

Ответ: Пр ba = 2.2.

Примеры вычисления проекции вектора для пространственных задачи

Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.

Решение:

Найдем скалярное произведение этих векторов

a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12

Найдем модуль вектора b

|b| = √42 + 22 + 42 = √14 + 4 + 16 = √36 = 6

Найдем проекцию вектора a на вектор b

Пр ba = a · b  = 12 = 2
|b|6

Ответ: Пр ba = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Проекция вектора на ось. Как найти проекцию вектора

Для понятия проекции вектора на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.

Предварительные сведения

Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу - его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем еще несколько понятий, связанных с понятием вектора.

Определение 3

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).

Определение 4

Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:

  1. Эти векторы коллинеарны.
  2. Если они будут направлены в одну сторону (рис. 3).

Обозначение: $\overline{a}↑↑\overline{b}$

Определение 5

Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:

  1. Эти векторы коллинеарны.
  2. Если они направлены в разные стороны (рис. 4).

Обозначение: $\overline{a}↑↓\overline{d}$

Определение 6

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Перейдем к определению равенства двух векторов

Определение 7

Два вектора будем называть равными, если они удовлетворяют двух условиям:

  1. Они сонаправлены;
  2. Их длины равны (рис. 5).

Геометрическая проекция

Как мы уже сказали ранее, результатом геометрической проекции будет вектор.

Определение 8

Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A'$ - начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B'$ - конец искомого вектора. Вектор $\overline{A'B'}$ и будет искомым вектором.

Рассмотрим задачу:

Пример 1

Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.

Решение.

Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A'$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B'$ (рис. 7).

Полученный на оси $l$ вектор $\overline{A'B'}$ и будет искомой геометрической проекцией.

Замечание 1

Заметим, что если угол между вектором и осью острый, то проекция сонаправлена с осью, а если тупой, то проекция противоположно направлена с осью.

Числовая проекция

Как мы уже знаем, результатом алгебраической проекции будет неотрицательное действительное число.

Определение 9

Числовой (алгебраической) проекцией на ось будем называть неотрицательное число, равное длине вектора геометрической проекции.

Рассмотрим это понятие на примере задачи:

Пример 2

Найти числовую проекцию вектора $\overline{F} на сонаправленную ему ось $x$, если угол между ними равняется $α$ (рис. 8). (рис. 8).

Решение.

Введем на рисунке следующие обозначения:

Видим, что длина вектора геометрической проекции, равняется длине $XY$. Из определения косинуса получим, что

$XY=|\overline{F}|cosα$

где $|\overline{F}|$ - длина вектора $\overline{F}$. Это и будет искомая алгебраическая проекция на ось.

Другие случаи можете видеть на рисунке 9.

spravochnick.ru

Проекция ( геометрическая , алгебраическая) вектора на ось. Свойства проекций.

Ответ:

Свойства проекций:

Свойства проекции вектора

Свойство 1.

Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:

Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот.

 

Свойство 2. Если вектор умножается на число λ, то его проекция на ось также умножается на это число:

Свойство 3.

Проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:

Орт оси. Разложение вектора по координатным ортам. Координаты вектора. Свойства координат

Ответ:

Орты осей.

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.

В трёхмерном случае орты обычно обозначаются

и Могут также применяться обозначения со стрелками и

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

Разложение вектора по координатным ортам.

Орт координатной оси обозначается через , оси - через , оси - через (рис. 1)

Для любого вектора который лежит в плоскости имеет место следующее разложение:

Если вектор расположен в пространстве, то разложение по ортам координатных осей имеет вид:

Координаты вектора:

Чтобы вычислить координаты вектора , зная координаты (x1; y1) его начала A и координаты (x2; y2) его конца B, нужно из координат конца вычесть координаты начала: (x2 – x1; y2 – y1).

Свойства координат.

Рассмотрим координатную прямую с началом координат в точке О и единичным вектором i. Тогда для любого вектора a на этой прямой: a = axi.

Число ax называется координатой вектора a на координатной оси.

Свойство 1.При сложении векторов на оси их координаты складываются.

Свойство 2.При умножении вектора на число его координата умножается на это число.

Скалярное произведение векторов. Свойства.

Ответ:

Скалярным произведением двух ненулевых векторов называется число,

равное произведению этих векторов на косинус угла между ними.

Свойства:

1. Скалярное произведение обладает переместительным свойством: ab=bа

 

Скалярное произведение координатных ортов. Определение скалярного произведения векторов, заданных своими координатами.

Ответ:

Скалярное произведение (×) орты

 

 

Определение скалярного произведения векторов , заданных своими координатами.

Скалярное произведение двух векторов и заданных своими координатами, может быть вычислено по формуле

Векторное произведение двух векторов. Свойства векторного произведения.

Ответ:

Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую., если нет то в противоположном ( показать как он показывал с «ручками»)

Векторным произведением вектора ана векторbназывается вектор с который :

1. Перпендикулярен векторам а иb

2. Имеет длину, численно равную площади параллелограмма, образованного на a и bвекторах

3. Векторы, a ,b, и c образуют правую тройку векторов

Свойства:

1.

2.

3.

4.

Векторное произведение координатных ортов. Определение векторного произведения векторов, заданных своими координатами.

Ответ:

Векторное произведение координатных ортов.

Определение векторного произведения векторов, заданных своими координатами.

Пусть векторы а = (х1; у1; z1) и b = (х2; у2; z2) заданы своими координатами в прямоугольной декартовой системе координат О, i, j, k, причем тройка i, j, k является правой.

Разложим а и b по базисным векторам:

а = x1i + y1 j + z1 k, b = x2 i + y2 j + z2 k.

Используя свойства векторного произведения, получаем

[а; b] = [x1 i + y1 j + z1 k ; x2 i + y2 j + z2 k] =

= x 1x2 [i; i] + x1 y2 [i; j] + x1 z2 [i; k] +

+ y1 x2 [j; i] + y1 y2 [j; j] + y1 z2 [j; k] +

+ z1 x2 [k; i] + z1 y2 [k; j] + z1 z2 [k; k]. (1)

По определению векторного произведения находим

[i; i] = 0, [i; j] = k, [i; k]= — j,

[j; i] = — k, [j; j] = 0, [j; k] = i,

[k; i] = j, [k; j] = — i. [k; k] = 0.

Учитывая эти равенства, формулу (1) можно записать так:

[а; b] = x1 y2 k — x1 z2 j — y1 x2 k + y1 z2 i + z1 x2 j — z1 y2 i

Или

[а; b] = (y1 z2 — z1 y2) i + (z1 x2 — x1 z2 ) j + (x1 y2 — y1 x2) k. (2)

Формула (2) дает выражение для векторного произведения двух векторов, заданных своими координатами.

Полученная формула громоздка .Используя обозначения определителей можно записать ее в другом более удобном для запоминания виде:

Обычно формулу (З) записывают еще короче:

 

stydopedia.ru

3. Проекция вектора на ось

3.1. Основные определения

Определение 3.1 Проекцией точки на прямую или плоскость называется основание перпендикуляра, проведенного из данной точки на прямую или плоскость (на рис. 3.1 точка– проекция точкиA, точка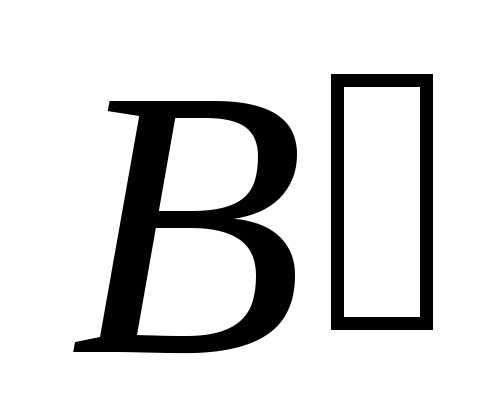– проекция точкиB).

Определение 3.2. Составляющей (компонентой) вектора по прямой (плоскости) называется вектор, лежащий на данной прямой (плоскости), начало и конец которого совпадают, соответственно, с проекциями начала и конца этого вектора (на рис. 3.1 вектор– составляющая вектора).

Определение 3.3. Проекцией вектора на ось называется скаляр, равный модулю составляющей вектора по этой оси, взятому со знаком плюс, если направление составляющей совпадает с направлением оси, и со знаком минус, если эти направления противоположны (рис. 3.2).

Рис. 3.2

Проекция вектора на ось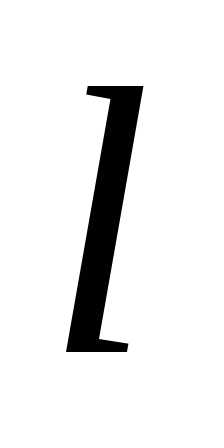обозначается символом:

или.

На рис. 3.2 (а) проекция векторана осьположительна, т.к. составляющая данного вектора по осисовпадает по направлению с осью,.

На рис. 3.2 (б) проекция равна нулю, т.к. начало и конец составляющей вектора совпадают,.

На рис. 3.2 (в) проекция вектора отрицательна, т.к. составляющая вектора направлена противоположно направлению оси,.

3.2. Свойства проекции вектора на ось

Проекция вектора на ось не изменится при параллельном переносе вектора.

Аддитивность проекции. Проекция суммы векторов на некоторую ось равна сумме проекций данных векторов на эту ось.

. (3.1)

.Однородность проекции. Скалярный множитель можно вынести за знак проекции вектора на ось,

. (3.2)

Следующему свойству предпошлем определение угла между вектором и осью.

Определение 3.4.Углом между вектором и осью называется угол между вектором и положительным направлением оси, отсчитываемый в направлении от оси против движения часовой стрелки(рис. 3.4).

.Проекция вектора на ось равна произведению модуля этого вектора на косинус угла между вектором и осью,(рис. 3.3).

(3.3)

Рис. 3.3

Проиллюстрируем применение свойств проекции вектора на ось к решению задачи.

Задача 3.1.Дано:,,,.

Найти: .

Решение. Применим свойства аддитивности и однородности проекции вектора на ось и формулу (3.2).

Ответ.

Эффективное практическое применение векторов, в том числе и с использованием компьютеров, связано с использованием пространственной системы координат.

4. Декартова прямоугольная система координат в пространстве

4.1. Общие определения, координаты вектора

Декартова прямоугольная система координат в пространстве определяется заданием трех взаимно перпендикулярных осей с общим началом отсчета (начало системы координат) и одинаковой для всех осей масштабной единицей (рис. 4.1). Оси носят название:

Плоскости xОy,xОz,yOzназываются координатными плоскостями.

Единичные векторы 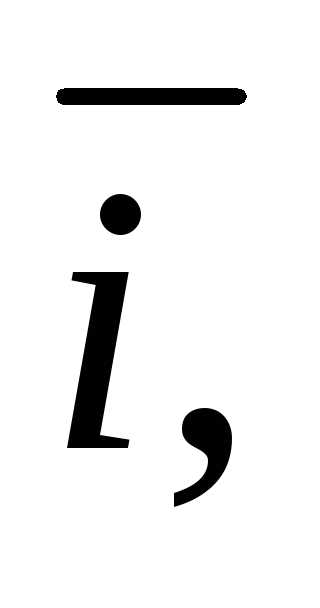,, сонаправленные с осямиOx,Oy,Oz, носят названиеортов осей.

Если орты образуют правую тройку, то система координат называется правой, если левую, то – левой.

Мы будем работать только с правой системой координат (рис. 4.1).

Определим понятие координат вектора. Рассмотрим произвольный вектор . Приведем его к началу координат, точке(рис. 4.1). Спроектируем этот вектор на координатные оси. Составляющими векторапо координатным осям являются векторы:, а проекциями на координатные оси – числа. Эти проекции носят названия координатами вектора.

Определение 4.1. Координатами вектора называются его проекциина координатные оси. При этом пишут:

(4.1)

где Очевидно, координаты нулевого вектора равны 0:

(4.2)

studfiles.net

Определение проекции вектора на плоскость

Задача взята из предлагаемых на сертификации по математике, проводимой порталом “Профи.ру” для репетиторов.

Задача. Чему равны координаты проекции вектора на плоскость, проходящую через точки , , ?

Уравнение плоскости определяется выражением:

   

Определим уравнение плоскости. Для этого составим систему:

   

Вычтем из первого уравнения второе:

   

   

Подставим это в первое уравнение, получим

   

Откуда

   

Подставляя найденное в третье уравнение, имеем:

   

   

   

Тогда уравнение плоскости будет выглядеть:

   

Это можно разделить на , и тогда мы получим:

   

Вектор, его проекция, плоскость и нормаль к ней.

Следовательно, нормаль к плоскости имеет координаты: , что означает, что лежит эта нормаль в плоскости, перпендикулярной оси , а значит,  сама плоскость ей параллельна. Это уже означает, что координата проекции заданного вектора на эту плоскость должна иметь вторую координату, равную -1 – координате исходного вектора. Остается найти его первую и третью координаты.

У нас есть уравнение плоскости – то есть координаты вектора нормали, и есть  координаты  двух точек (начала и конца вектора). Тогда можно записать каноническое уравнение прямой, проходящей через данную точку параллельно нормали. Составим два таких уравнения – для точек начала и конца вектора, тогда, решив такое уравнение совместно с уравнением плоскости, получим координаты точек, где прямые, параллельные нормали и проходящие через конец и начало вектора, «протыкают» плоскость, а это и будут точки конца и начала вектора проекции.

Общий вид уравнения:

   

Пусть координаты начала вектора проекции , координаты конца  .

Для конца заданного вектора это уравнение будет выглядеть так:

   

Из этого уравнения имеем:

   

Уравнение плоскости преобразуем к виду:

   

Решим эти два уравнения совместно:

Из последнего

   

Подставим в уравнение прямой:

   

Откуда

   

Тогда

   

Это нами были найдены координаты конца вектора проекции. Найдем координаты его начала, повторяем все действия, помня, что начало заданного вектора совпадает с началом координат:

   

Из этого уравнения имеем:

   

Подставим в уравнение прямой:

   

Откуда

   

Тогда

   

Осталось просто вычесть из координат конца координаты начала:

   

   

Ответ: вектор проекции на плоскость имеет координаты (9; -1; 6).

easy-physic.ru