Степень с натуральным показателем и её свойства. С разными основаниями степени
МАТВОКС ⋆ Сравнение степеней с одинаковым показателем степени и разными основаниями ⋆ Энциклопедия математики
Если a и b – положительные числа, то для любого положительного n справедливо неравенство:
т.е. из двух степеней с одинаковым положительным показателем степени n меньше та, основание которой меньше, и больше та, основание которой больше.
Если a и b – положительные числа, то для любого не положительного n (n≤0) справедливо неравенство:
т.е. из двух степеней с одинаковым отрицательным показателем степени n больше та, основание которой меньше, и меньше та, основание которой больше.
Если a и b – положительные числа, то для любого положительного m/n справедливо неравенство:
т.е. из двух степеней с одинаковым положительным показателем степени m/n меньше та, основание которой меньше, и больше та, основание которой больше.
Если a и b – положительные числа, то для любого не положительного m/n (m/n≤0) справедливо неравенство:
т.е. из двух степеней с одинаковым отрицательным показателем степени n больше та, основание которой меньше, и меньше та, основание которой больше.
mathvox.ru
Свойства степени с одинаковыми основаниями.
Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени - достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.

Свойства степени
Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.
1-е свойство.
а0 = 1
Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.
2-е свойство.
а1 = а
3-е свойство.
аn * am = a(n+m)
Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.
4-е свойство.
an/am = a(n-m)
Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.
Свойство работает только при делении, при вычитании не применяется!
5-е свойство.
(an)m = a(n*m)
6-е свойство.
a-n = 1/an
Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.
7-е свойство.
(a*b)m = am * bm
Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.
8-е свойство.
(a/b)n = an/bn
9-е свойство.
а½ = √а
Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.
Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.
10-е свойство.
(√а)2 = а
Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.
11-е свойство.
n √an = a
Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.
12-е свойство.
am/n = n √am
Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.
Применение степеней и их свойств
Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.
Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.
Формулы сокращенного умножения - еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.
Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.
Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.
Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.
С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.
Показательные уравнения и неравенства
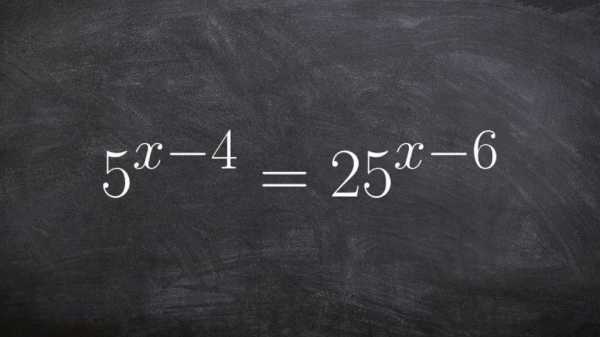
Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.
fb.ru
Свойства степеней | Алгебра
Основные свойства степеней задаются формулами:
(При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают).
(При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя).
(При возведении степени в степень основание оставляют прежним, а показатели перемножают).
(При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают).
(При возведении в степень частного возводят в эту степень и делимое, и делитель, результаты делят).
Кроме того,
(где a≠0)
Если n — натуральное число, то
в частности,
в частности,
Для a>0
В частности,
В школьном курсе алгебры свойства степеней изучаются на протяжении нескольких лет: сначала для степени с натуральным показателем, затем — для степени с целым показателем, далее — для степени с рациональным и иррациональным показателем.
Свойства степеней с натуральным и целым показателем верны и для степеней с рациональными и иррациональными показателем, но накладывается дополнительное условие: основания степеней в этом случае должны быть положительными.
По определению, для любого α
www.algebraclass.ru
Свойства степеней с натуральными показателями. Натуральная степень. Степени чисел. Свойства показателей степеней
Свойства степеней с натуральными показателями
Говоря про свойства степеней, считаем, что числа a и b действительные, а числа m и n натуральные.
Свойства степеней с натуральными показателями:
Свойство 1.
1. При умножении степеней с одинаковыми основаниями, показатели степеней складываются:aman = am + n
Пример умножения степеней с одинаковыми основаниями:
52 * 53 =52 + 3 =55
Обратите внимание на то, что основания степеней одинаковые, оба равны 5-ти.
Свойство 2.
2. Если степень возводится в степень, то показатели перемножаются:(am)n = am * n
Пример возведения степени в степень:
(52)4 =52 * 4 =58
То есть при возведении степени в степень показатели перемножаются.
Свойство 3.
3. Если основания степеней разные, а показатели одинаковые, то произведение степеней равно степени произведения:ambm = (ab)m
Пример произведения степеней:
42 * 32 =(4 * 3)2
То есть произведение степеней равно степени произведения.
Свойство 4.
4. Частное степеней с одинаковыми основаниями, m > n:am : an = am - n
Пример частного степеней с одинаковыми основаниями:
106 : 104 =106 - 4 = 102 = 100
То есть основание остается, а показатели степеней вычитаются.
Свойство 5.
5. Если основания степеней разные, а показатели одинаковые, то частное степеней равно степени частного:an : bn = (a/b)n
Пример частного степеней с разными основаниями и одинаковыми показателями:
52 : 62 =(5/6)2
То есть частное степеней с одинаковыми показателями равно степени частного.
www.sbp-program.ru
Степень с натуральным показателем и её свойства
Степень с натуральным показателем и ее свойства.
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:
an =
В выражении an :
- число а (повторяющийся множитель) называют основанием степени
- число n (показывающее сколько раз повторяется множитель) – показателем степени
Например: 25 = 2·2·2·2·2 = 32, здесь: 2 – основание степени, 5 – показатель степени, 32 – значение степени
Отметим, что основание степени может быть любым числом.
Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 108
Каждое число большее 10 можно записать в виде: а · 10n , где 1
Например: 4578 = 4,578 · 103 ;
103000 = 1,03 · 105.
Свойства степени с натуральным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются
am · an = am + n
например: 71.7 · 7 - 0.9 = 71.7+( - 0.9) = 71.7 - 0.9 = 70.8
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются
am / an = am — n ,
где, m > n,
a ? 0
например: 133.8 / 13 -0.2 = 13(3.8 -0.2) = 133.6
3. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.
например: (23)2 = 2 3·2 = 26
4. При возведении в степень произведения в эту степень возводится каждый множитель
(a · b)n = an · b m ,
например:(2·3)3 = 2n · 3 m ,
5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель
(a / b)n = an / bn
например: (2 / 5)3 = (2 / 5) · (2 / 5) · (2 / 5) = 23 / 53
mirurokov.ru
Как сравнивать степени | Логарифмы
Как сравнивать степени с одинаковыми основаниями? С одинаковыми показателями? Можно ли сравнить степени, если и основания, и показатели различны?
Как и сравнение логарифмов, сравнение степеней основано на свойстве показательной функции.
Сравнение степеней с одинаковыми основаниями
- Если основание степени больше единицы (a>1), показательная функция возрастает, большему значению аргумента соответствует большее значение функции, соответственно, знак неравенства между показателями степеней и между степенями одинаковый.
- Если основание степени меньше единицы (0<a<1), функция убывает, большему значению аргумента соответствует меньшее значение функции, знак неравенства между показателями степеней противоположен знаку между степенями.
С помощью схемы сравнение степеней с равными основаниями можно изобразить так:
Примеры.
№1. Сравнить значения выражений:
Решение:
Сравниваем показатели степеней: 1,5<1,9.
Основание a=2/7 меньше единицы, функция убывает, знак неравенства между степенями меняется на противоположный:
Решение:
Сравниваем показатели степеней:
Основание a=5,2 больше единицы, функция возрастает, знак неравенства между степенями не меняется:
№2. Сравнить показатели m и n, если известно, что для степеней выполняется неравенство:
Решение:
Основание a=0,21<1, функция убывает, поэтому знак неравенства между показателя степеней нужно изменить на противоположный: m>n.
Решение:
Основание
функция возрастает, поэтому знак неравенства между показателями степеней не изменяется: m<n.
Сравнение степеней с одинаковыми показателями.
1) Для возрастающих функций ( x>0):
Пример.
Для положительных значений аргумента
например,
Для отрицательных значений аргумента
например,
2) Для убывающих функций:
Пример.
Для положительных значений аргумента
например,
Для отрицательных значений аргумента:
например,
Как сравнивать степени, если и основания, и показатели различны?
Можно попробовать, например, сравнить каждую из степеней с единицей. Любая степень с основанием, большим единицы, при положительных значениях аргумента принимает значения, большие единицы:
при отрицательных — меньшие 1:
Если основание меньше единицы — соответственно,
Пример.
Сравнить
Решение:
В алгебре сравнивать степени чаще всего приходится при решении показательных неравенств.
Как решать показательные неравенства, мы рассмотрим позже.
www.logarifmy.ru
Свойства степени
Наверное, ни для кого не является секретом, что большинство математических утверждений, прежде, чем установится, проходят несколько этапов. Давайте подробно рассмотрим, как же.
Первый этап – это, конечно же, когда человек замечает некоторую одну и ту же закономерность в ряде случаев.
Второй этап – формулировка закономерности. Говоря проще, человек пытается предположить, что данная закономерность действует не только в одном конкретном случае, а и во всех подобных.
Третий этап – человек пытается доказать то, что закономерность, которую он подметил, а потом сформулировал, верна, то есть он пытается ее доказать. Но что же значит доказать, что утверждение верно? Конечно же, это значит объяснить верность предположений, но при этом опираться необходимо обязательно только лишь на уже проверенные факты, теоремы и утверждения.
Теперь давайте рассмотрим подробнее, непосредственно, свойства степеней.
Итак, первое свойство: aH * aK = aH+K
Проверим данное свойство на примере: 22 * 23 = 22+3. Как видим, утверждение правильное. Мы можем взять еще несколько подобных примеров, и все время будет получать только лишь верный результат.
Второе свойство (подобное к первому, за исключением нескольких различий в знаках). В данном случае мы будем иметь дело с делением: aH : aK = aH-K
Проверяем данное свойство также на примере: : 22 : 23 = 22-3. Опять-таки получили верный результат.
Третье свойство: (aH)K = aH*K
Опять же проверяем на примере: (22)3 = 26. Получили очередное правильное свойство.
Исходя из вышеуказанных формул и примеров, легко выводятся три основных правила, связанные со свойством степеней:
- Если у степени одинаковое основание, показатели разные, а сами основания умножаются, то мы можем преобразоваться это в степень с одним основанием, а показатели степени просто суммируются.
- Если у степени одинаковое основание, показатели разные, а сами основания делятся, то мы можем преобразоваться это в степень с одним основанием, а показатели степени просто вычитаются.
- Если мы хотим возвести степень в степень, то необходимо просто перемножить показатели степени.
Например: 2^2+3^2
| Свойства степени | |||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
|
mateshka.ru