Площадь сектора круга. Радиус круга формула через площадь
Формула площади круга
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность, а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
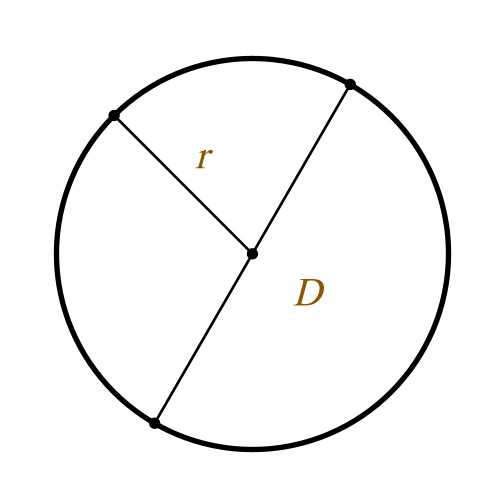
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
r – радиус круга
D – диаметр круга
S – площадь круга
π – 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг. К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг. Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга, а впервые они стали строиться еще во времена античности. Само слово «circus» в переводе с латинского языка означает «круг». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол», которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
simple-math.ru
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b - верхнее основание
a - нижнее основание
c - равные боковые стороны
α - угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R - радиус вписанной окружности
D - диаметр вписанной окружности
O - центр вписанной окружности
H - высота трапеции
α, β - углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d - диагональ трапеции
α, β - углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m - средняя линия трапеции
c - боковая сторона
α, β - углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b - верхнее основание
a - нижнее основание
h - высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
www-formula.ru
Площадь сектора круга - формула, пример расчета
Сектор круга – это плоская фигура, ограниченная дугой и радиусами, соединяющими концы дуги с центром круга.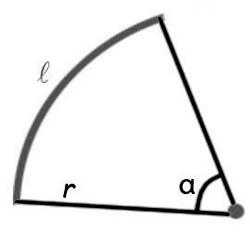
Существует две формулы площади сектора круга. Расчеты могут производиться как через длину дуги, так и через угол между радиусами. Если известна длина дуги, то применяется такая формула:
Когда дан угол между ограничивающими сектор радиусами, расчет площади представляет собой произведение площади круга на соотношение угла между радиусами к углу полной окружности, т.е. 360°.Рассмотрим пример расчета площади сектора круга по обеим формулам.
Площадь сектора кольца
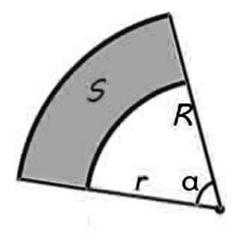Сектор кольца – это плоская фигура, которая располагается в окружности и ограничивается двумя дугами разного радиуса и линиями, проведенными от центра к большей дуге.Формула площади сектора кольца представляет собой разность площадей большего и меньшего сектора круга.
Если дан угол α, то площадь сектора кольца можно найти по следующей формуле:
Рассмотрим пример расчета площади сектора кольца.
Пусть дана окружность с радиусом 5 см. Сектор кольца ограничен углом α = 45°, а радиус меньшего сектора равен r = 3 см. Найдем площадь. Из условий задачи мы понимаем, что больший радиус равен радиусу окружности, то есть R = 5 см. Подставим данные в формулу:Расчет площади шарового сектора
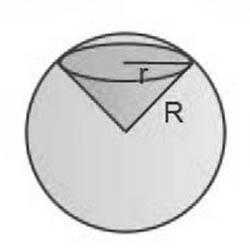Шаровым сектором называют часть шара, которая ограничивается кривой поверхностью шарового сегмента и конической фигурой, вершиной которой является центр шара, а основанием – шаровой сегмент.Чтобы вывести формулу площади шарового сектора, потребуется найти высоты конуса и сегмента. Она легко вычисляется по теореме Пифагора. Для этого необходимо знать радиус шара и радиус основания конуса. Обозначим радиус шара как R, а радиус сегмента – r. ТогдаПлощадь сектора – это сумма площадей конуса и сегмента. Подставим выведенные формулы в общую:
Рассмотрим пример расчета площади поверхности шарового сектора.
Пусть дан шар с радиусом R = 4 см, в котором выделен сектор с радиусом основания r = 1,5 см. Найдем площадь. Подставляем все данные в формулу и производим расчеты:2mb.ru
