Медиана, высота и биссектриса треугольника. Формула длина биссектрисы
Все формулы биссектрисы в треугольнике
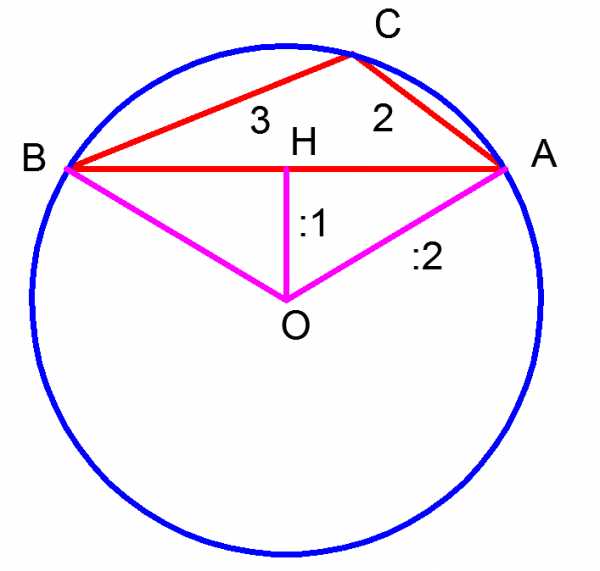
L- биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b - стороны треугольника
с - сторона на которую опущена биссектриса
d, e - отрезки полученные делением биссектрисы
γ - угол ABC , разделенный биссектрисой пополам
p - полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
Подробности Автор: Administrator Опубликовано: 06 октября 2011 Обновлено: 16 мая 2017Свойство биссектрисы угла треугольника
СОДЕРЖАНИЕ
Введение……………………………………………………………………. 2
Свойство биссектрисы треугольника и способы
доказательства …………………………………………………………4
Нахождение длины биссектрисы (формулы) ………………………7
Соотношения, связанные с биссектрисой………………………..…...13
4.Задачи…………………………………………………………………….16
5. Выводы…………………………………………………………………..20
6. Список литературы…………………………………………………….21
ВВЕДЕНИЕ
Цель работы:
Показать многообразие способов доказательства свойства биссектрисы треугольника.
Задачи:
Ознакомиться с литературой по данной теме, повторить ряд геометрических фактов, необходимых для проекта
Систематизировать теоретический материал, используемый для доказательства теоремы
Выяснить практическое применение формул для вычисления биссектрисы треугольника
Создание презентации к работе
Что мы знаем о биссектрисе угла треугольника? Наверное не так уж и много – определение биссектрисы; факт, что точка пересечения биссектрис является центром вписанной в треугольник окружности и свойство деления стороны биссектрисой на отрезки пропорциональные прилежащим сторонам.
В своей работе я постаралась систематизировать сведения и найти дополнительную информацию, которая углубляет знания об этом понятии в теории треугольников. С помощью научной литературы по теме и работы с научным руководителем, мы привели несколько способов доказательства свойства биссектрисы треугольника. При этом использовали следующие теоремы и понятия:
1.Теорему Фалеса о пропорциональных отрезках
2. Подобие треугольников
3. Применение формул площадей треугольника
4. Теорема синусов
Доказательство теоремы разными способами позволят повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приемов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.
В работе значительно расширены сведения о биссектрисах треугольника:
приводятся 4 вида формул для вычисления биссектрисы треугольника, эти формулы имеют практическое применение;
выводятся формулы радиуса окружности, вписанной в треугольник;
формулируются свойства точки пересечения продолжения биссектрисы треугольника с описанной окружностью;
устанавливается взаимное расположение высоты, медианы и биссектрисы треугольника, проведенных из одной вершины ( 3 способа).
.
РАЗДЕЛ 1
Свойство биссектрисы треугольника и способы его доказательства.
Теорема.
Биссектриса делит сторону треугольника на отрезки пропорциональные двум другим сторонам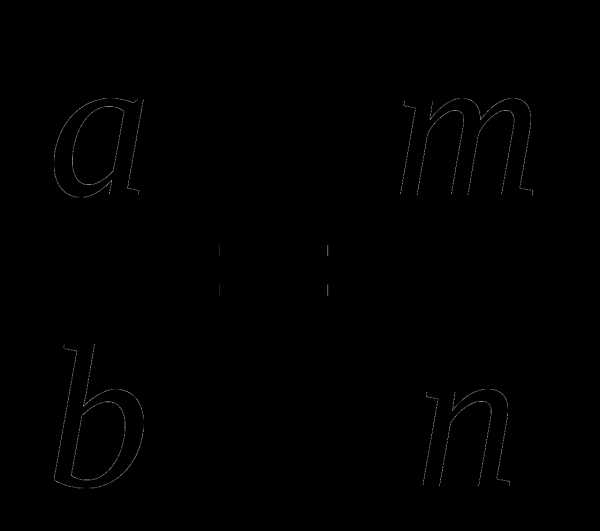 
.
Дано: ∆ АВС, BD – его биссектриса.
Доказать: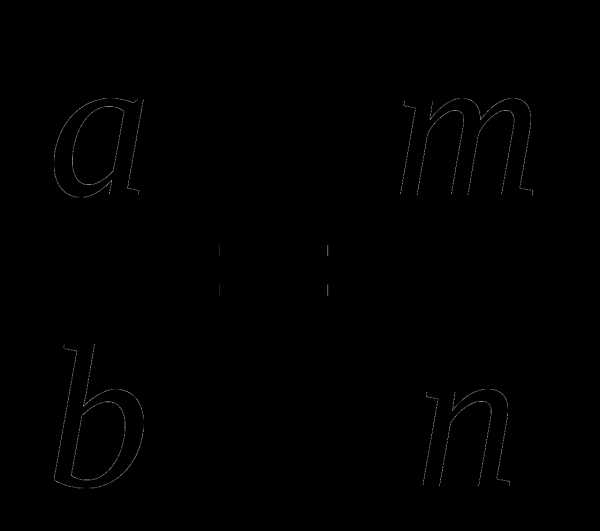
1. Применим к доказательству теорему Фалеса
Проведем прямую CK||BD и продолжим сторону AB до пересечения с этой прямой. 2 = 3 как внутренние накрест лежащие при параллельных прямых BD и KC и секущей BC. 1 = 4 как соответственные углы при CK||BD и секущей BC.
∆ BCK – равнобедренный.
Тогда по теореме Фалеса: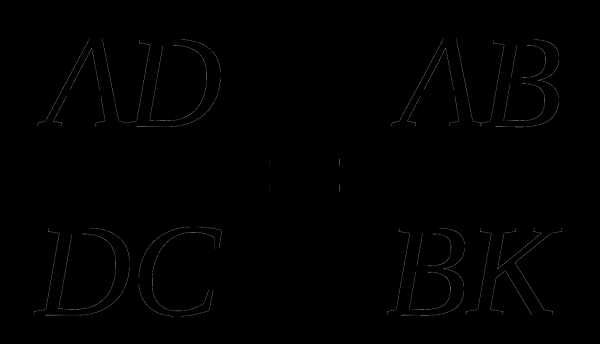 
Т.е 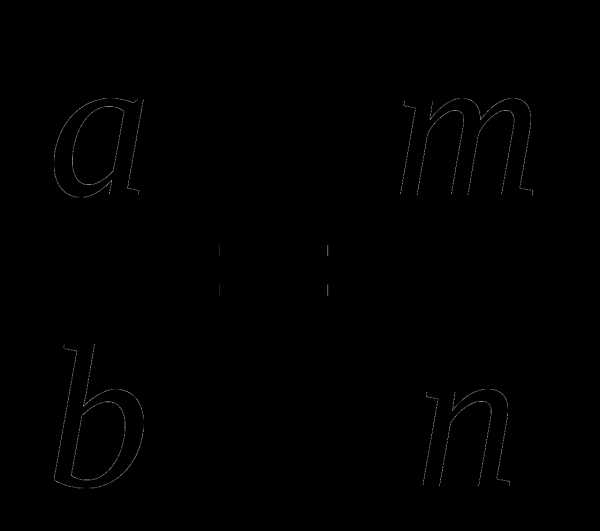, что и требовалось доказать
Применим подобие треугольников (рис. 1.2)
Проведем перпендикуляры из вершин А и С на биссектрису и ее продолжение, тогда имеем:
Рис. 1.2
∆ AND ~ ∆ CMD (по двум углам). Из определения подобия треугольников следует пропорциональность соответствующих сторон:
, 
(*)
∆ ABN~ ∆ CBM, тогда 
; 
В равенствах (*) и (**) равны правые части, а значит: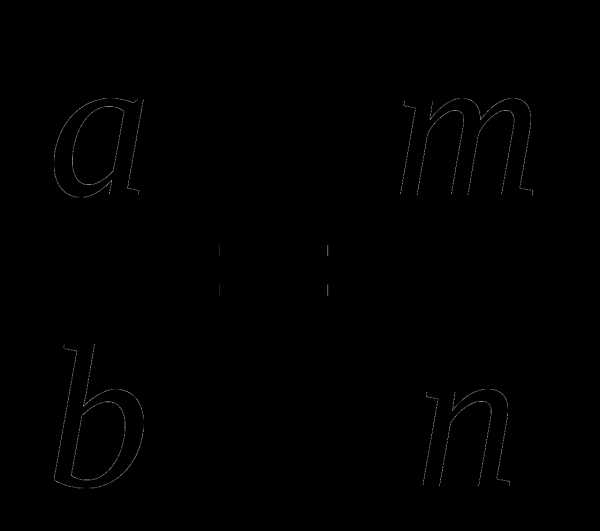
Применим формулы площади треугольника (рис. 1.3)
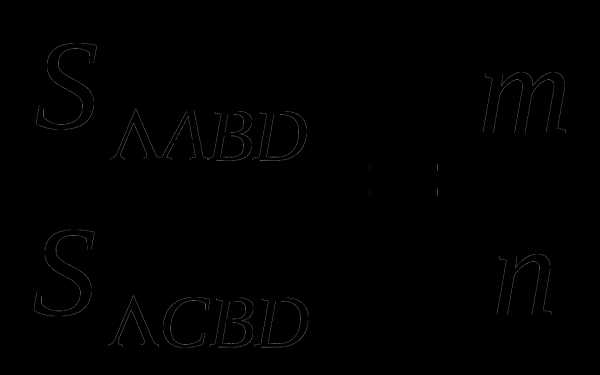
Точка D лежит на биссектрисе угла ABC, значит она равноудалена от его сторон, то есть 
Тогда: 
Получили, что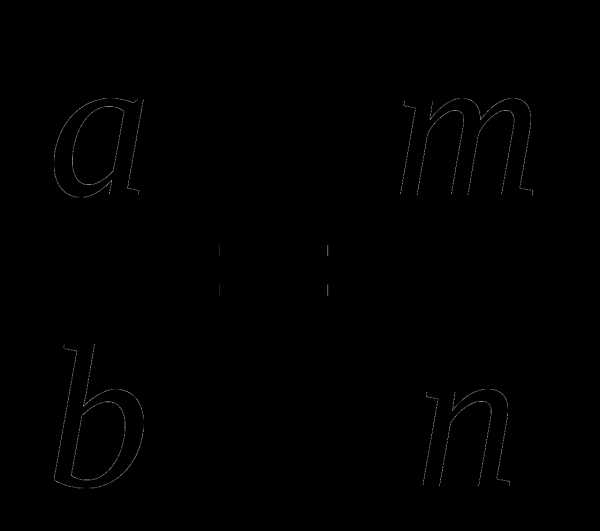
4. Применим теорему синусов
Рис. 1.4
Из ∆ ABD по теореме синусов: 
, или упростив, имеем: 
(*)
Из ∆ BDС по теореме синусов: 
(**)
Разделим равенство (*) на (**), получим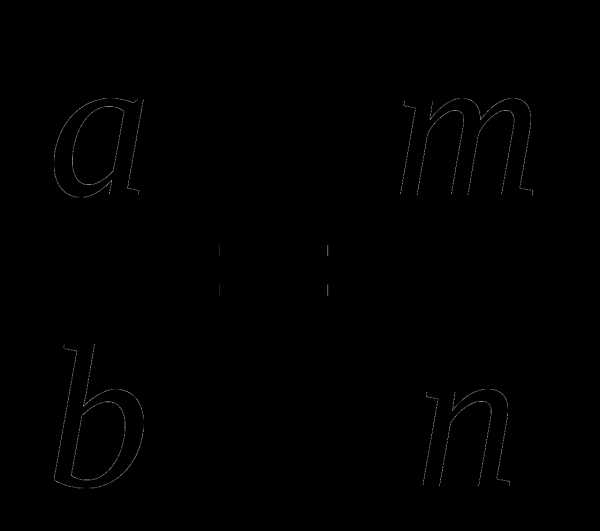
. 5. Докажем теорему, используя формулы площади треугольника (рис. 1.4)
Получили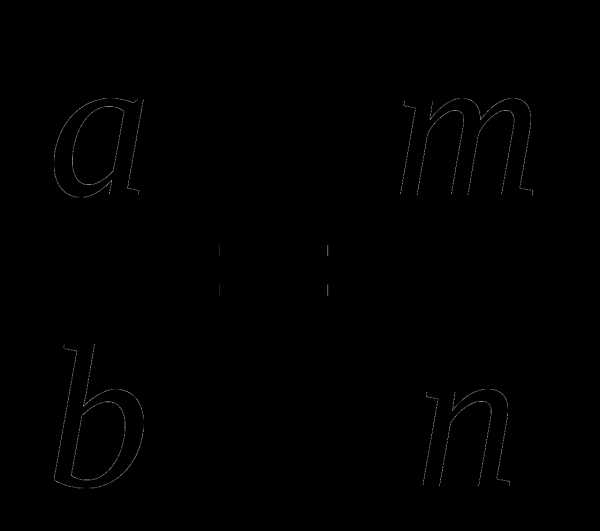
РАЗДЕЛ 2
Формулы для вычисления длины биссектрисы
В разделе выводятся четыре формулы для вычисления длины биссектрисы треугольника [3].
2.1. Длина биссектрисы через пропорциональные стороны и отрезки
Рис. 2.1.1.
2.1.1.Доказательство. I способ - через вписанные углы (рис. 2.1.1).
Опишем вокруг ∆ABC окружность и продолжим биссектрису CD =l до
пересечения с окружностью, F – точка пересечения. Пусть DF= x.
Вписанные углы BFC и CAB равны, так как опираются на одну и ту же дугу BC. Тогда ∆FCB ~ ∆ACD по двум углам. У подобных треугольников соответствующие стороны пропорциональны:
или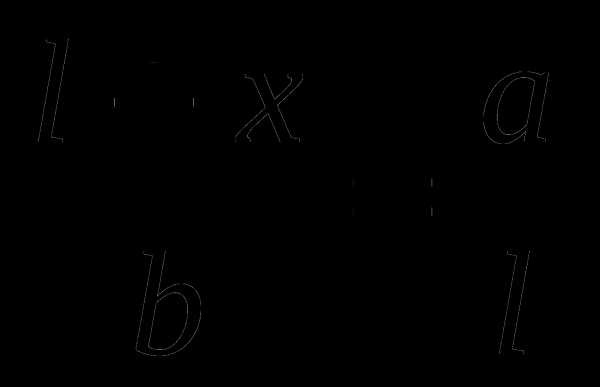 
Тогда (1).
По свойству пересекающихся хорд
или .
Подставим последнее равенств в формулу (1), получим
2.1.2.Доказательство. II способ – через теорему косинусов (рис.2.1.2)
Рис 2.1.2
Из пропорции 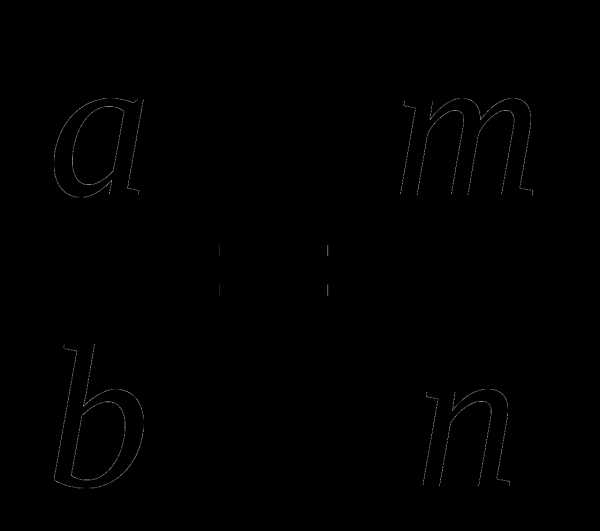следует, что 
, 
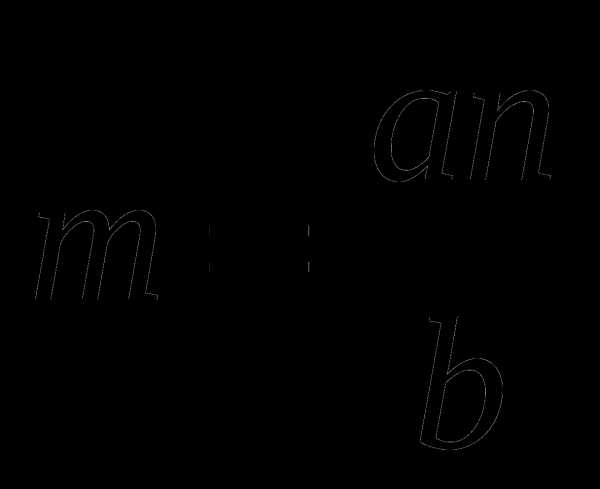(2).
Из ∆ BCD из теоремы косинусов.
Из ∆ DCA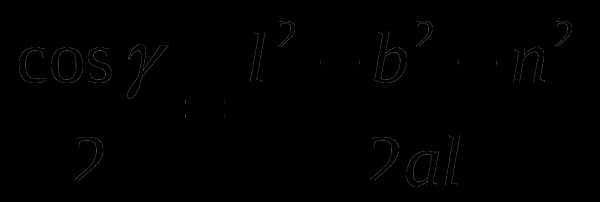 
.Получим равенство .
После умножения на 2abl получим:
Перегруппировка слагаемых
. Подставим формулы (2) в равенство вместо m и n
В случае, если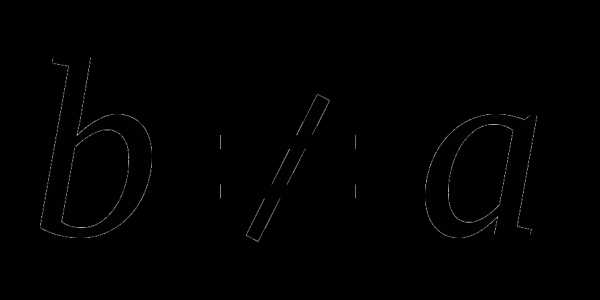 
делим на (b – a) и получаем
2.2. Длина биссектрисы через две стороны и угол между ними (рис. 2.2)
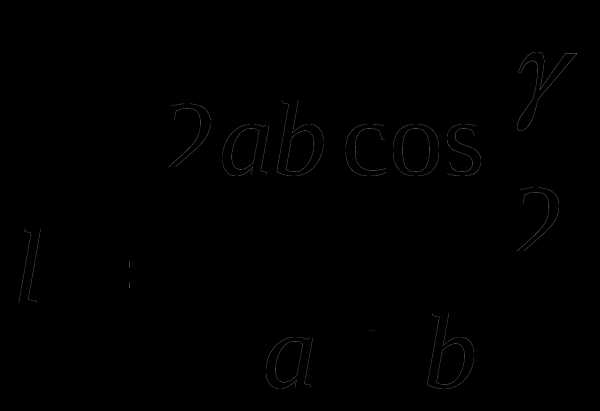
Рис. 2.2
Доказательство через площадь треугольника.
.
Равенство умножим на 2, а 
заменим по формулам двойного угла
Так как 
разделим на него и найдём l. ;
Следствие. В прямоугольном треугольнике угол , поэтому биссектриса опущенная на гипотенузу равна , где a и b – катеты.
Длина биссектрисы через стороны треугольника (рис. 2.3)
Рис. 2.3
Выразим отрезки m и n через стороны треугольника, решив систему.
; ; ; =c ; .
Аналогично .
Подставим найденные выражения в формулу биссектрисы
Тогда .
Угол между высотой и биссектрисой треугольника , проведенными
из одной вершины [1]
Рис. 2.4
Пусть CM= h – высота, а CD= l биссектриса треугольника, проведенная из той же вершины. Найдем угол MCD между высотой и биссектрисой треугольника.
Из
Из ∆BCM () BCM =
MCD= BCD - BCM = .
2.5.Длина биссектрисы через высоту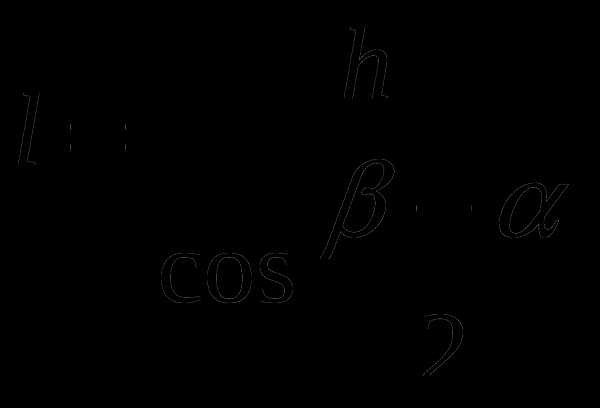 
(рис. 2.4)
Из ∆CMD () .
РАЗДЕЛ 3
Соотношения, связанные с биссектрисой
В разделе будет получено отношение, в котором биссектрисы треугольника делятся точкой пересечения; найден угол, образованный при пересечении биссектрис; установлена связь между сторонами треугольника и отрезками касательных ко вписанной в треугольник окружности.
3.1. Отношение , в котором биссектрисы треугольника делятся точкой пересечения (рис. 3.1)
Известно, что медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. Найдём, в каком отношении делятся биссектрисы точкой пересечении.
Рис. 3.1
Дано: биссектрисы CD и AM ∆АВС пересекаются в точке I (инцентр)
Пусть CI = x, а ID = y. Найдём отношение .
Из ∆ CDB по свойству биссектрис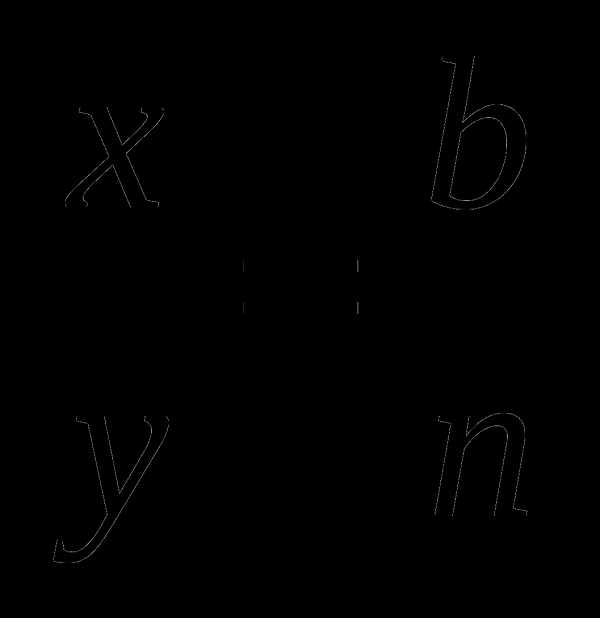 
. Учитывая что 
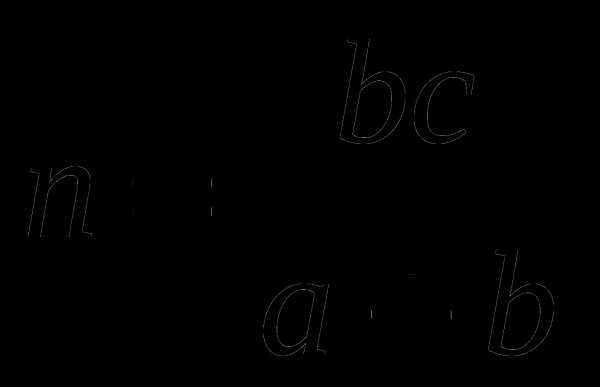, находим .
Получили соотношение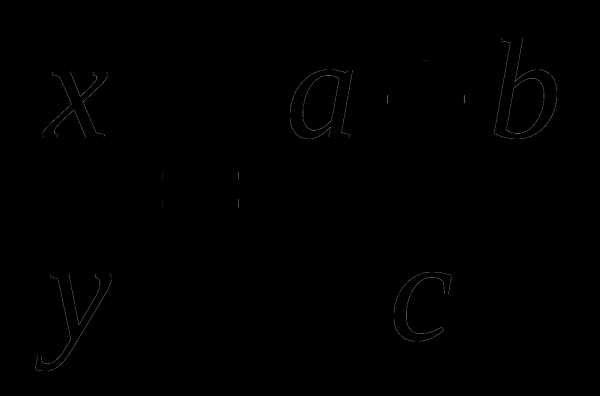 
Угол , образованный при пересечении биссектрис,
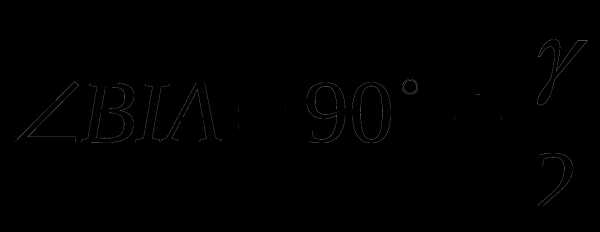
(рис. 3.2)
Рис. 3.2
Из 
:
3.3 . Связь между сторонами треугольника и отрезками касательных к вписанной в треугольник окружности (рис. 3.3)
Рис. 3.3
В ∆АВС вписана окружность. Пусть М,К, N – точки касания окружности сторон треугольника. По свойству отрезков касательных, проведенных из одной точки, AM=AK=x, CM=CN=y, NB=KB=z . Тогда
.
Сложив уравнения системы, получим
, где р – полупериметр.
Вычитая из последнего равенства уравнения системы, получим
Формулы, выражающие отрезки касательных через стороны треугольника.
Привожу без доказательства утверждения о свойстве точки пересечения продолжения биссектрисы треугольника с описанной около него окружностью, о расположении биссектрисы треугольника. Эта часть работы будет продолжена.
1. Точка пересечения продолжения биссектрисы треугольника с описанной около него окружностью, равноудалена от двух других вершин и инцентра
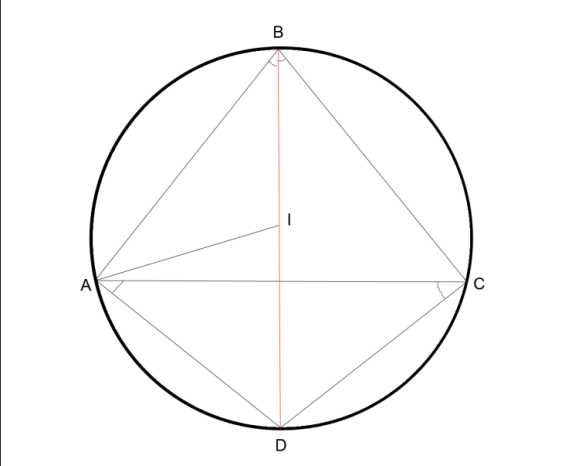
2. В неравнобедренном треугольнике биссектриса всегда расположена между высотой и медианой, проведенными из одной вершины.
Задачи
1. Дан треугольник ABC, в котором угол В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь треугольника ABD (рис. 1).
Рис. 1
Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.
Пусть AD = 2х; DC = Зх.
Ответ: 12/5.
Задача.
Стороны треугольника равны 10 см, 11 см и 12 см. Найти отрезки, на которые делит биссектриса треугольника среднюю сторону.
Дано: AC=10 см, BC=11 см, AB=12 см, AP = биссектриса.
Найти: CP и BP.
Решение:
По свойству биссектрисы треугольника:
Пусть CP=x см, тогда BP=11-x см:
откуда по основному свойству пропорции
CP=5 см, BP=6 см.
Ответ: 5 см, 6 см.
Найти биссектрису угла B треугольника ABC и определить, в каком отношении центр вписанной в треугольник окружности делит эту биссектрису, если AB = 4, BC = 5 и AC = 6.
Решение
Пусть BD и AK – биссектрисы углов B и A треугольника ABC и O – центр вписанной окружности. Так как AB = 4 и BC = 5, то по теореме о биссектрисе AD = 4t и CD = 5t, поэтому AC = 6 = 4t + 5t, т.е. , и тогда .
и
, т.е. .
И, наконец, определим по теореме о биссектрисе из треугольника BAD, в каком отношении точка O делит отрезок BD:
.
Ответ: и .
Найти биссектрисы острых углов в прямоугольном треугольнике, катеты которого равны 6 и 8 см.
Решение
Пусть ABC – прямоугольный треугольник, у которого AB = 6, BC = 8, B = 90 °, P и H – основания биссектрис углов C и A соответственно. Тогда по теореме Пифагора . По теореме о биссектрисе BP = 8t и Pa = 10t , откуда AB = AB = 6 = 8t + 10t и . Поэтому , и по теореме Пифагора . Аналогично находим .
Ответ: см, см.
ВЫВОДЫ
В этой работе мы показали разнообразие способов доказательства свойства биссектрисы треугольника. Выведена формула для вычисления длины биссектрисы, рассмотрен ряд задач, которые были в заданиях на ЕГЭ разных лет. Доказано положение биссектрисы в неравнобедренном треугольнике. Показано отношение , в котором биссектрисы треугольника делятся точкой пересечения; определен угол , образованный при пересечении биссектрис. Для многих свойств приводится несколько способов доказательства.
Работая над проектом и находя различные способы доказательств, приобретаются логические навыки, умение анализировать и сопоставлять, сравнивать. С помощью доказанных свойств многие задачи решаются легче и доступней.
Данная работа может служить справочным материалом при подготовке к ЕГЭ, как в теоретическом, так и в практическом плане.
СПИСОК ЛИТЕРАТУРЫ
Шарыгин И.Ф. Учимся решать задачи по геометрии //Математика в школе.-1989.-№2. –С. 87-89.
Мерзляк А.Г., Полонский В.Б., Якир М.С. Геометрия .8 класс: Учебник. Харьков: Гимназия,2008.- С.83-84.
Биссектриса треугольника.- [Электронный ресурс] .-режим доступа: ru.wikipedia.org/
Апостолова Г.В. Геометрия .8 класс: Учебник. Киев: Генеза, 2008.-С.36-37.
infourok.ru
Свойства биссектрисы треугольника | Подготовка к ЕГЭ по математике
Категория: ВидеоурокиПланиметрияСправочные материалы
Елена Репина 2013-03-15 2015-11-24Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
Свойства биссектрисы
1. Биссектриса треугольника делит угол пополам.
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()
3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.
4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
Некоторые формулы, связанные с биссектрисой треугольника
(доказательство формулы – здесь), где — длина биссектрисы, проведённой к стороне , — стороны треугольника против вершин соответственно, — длины отрезков, на которые биссектриса делит сторону ,
Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.Задачи, рассматриваемые в видеоролике:1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1
Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы
Автор: egeMax | комментария 2 | Метки: биссектрисаegemaximum.ru
Репетитор по математике и физике » Медиана, высота и биссектриса треугольника
Автор Сергей
Среда, Сентябрь 12, 2012
Для решения задач по геометрии, связанных с треугольниками, важно усвоить одну простую, но важную истину. Существует третий признак равенства треугольников («по трем сторонам»), из которого следует, что не существует двух различных треугольников с одинаковыми сторонами. Следовательно, зная длины всех сторон треугольника, можно узнать об этом треугольнике все, что нужно. В том числе длины его медиан, биссектрис и высот. Разберем более подробно, каким образом это можно сделать.
Теорема о длине высоты треугольника
Для нахождения длины высоты треугольника можно расписать его площадь двумя способами. Во-первых, используя формулу Герона, во-вторых, как половину произведения высоты на основание, к которому проведена данная высота.
здесь — полупериметр треугольника.
Из сравнения данных формул находим:
Отметим, что это лишь один из способов нахождения длины высоты треугольника по его сторонам, который удобен далеко не всегда. Существует огромное множество альтернативных способов, с которыми читатель может ознакомиться в предыдущих уроках.
| Пример 1. Известно, что расстояние от центра описанной окружности до стороны AB треугольника ABC равняется половине радиуса этой окружности. Найдите высоту треугольника ABC, опущенную на сторону AB, если она (высота) меньше а две другие стороны равны 2 и 3.
|
Решение. Треугольник BOA на рисунке является равнобедренным, поэтому ∠ OAH = ∠ OBH = 30° (катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы). Тогда ∠ BOA и соответствующая дуга окружности, на которую он опирается, равны по 120°. Тогда дуга, на которую опирается ∠ BCA, равна 240°, а значит сам угол ∠ BCA = 120°.
Площадь треугольника ABC находим по формуле: Длину стороны AB находим по теореме косинусов для треугольника ABC, она равна . С другой стороны, площадь треугольника есть половина произведения высоты на основание, к которому данная высота проведена. Отсюда выражаем требуемую длину высоты что меньше Случай с остроугольным треугольником ABC не подходит. Проверьте самостоятельно.
Задача для самостоятельного решения №1. В остроугольном треугольнике ABC BC = a, AC = b, ∠ ACB равен α. Найти высоту CD и ∠ ABC.
Показать ответОтвет:
Теорема о длине медианы треугольника
Медиана треугольника определяется через три его стороны по формуле:
где a, b, c — стороны треугольника, ma — медиана, проведенная к a. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.
| Пример 2. В треугольнике ABC со стороной AB = из вершины B к стороне AC проведены медиана BM = и высота BH = 2. Найдите сторону BC, если известно, что ∠ B + ∠ C < 90°.
|
Решение. Из анализа условия задачи делаем вывод, что ∠ A — тупой. Действительно, ведь сумма всех углов в треугольнике равна 180°. Находим по теореме Пифагора длину HA = 1. Далее по теореме Пифагора находим длину HM = 2. Следовательно, AM = HM — HA = 1. При этом AM = MC = 1 (т. к. BM — медиана). Итак, HC = HA + AM + MC = 3. Следовательно, по теореме Пифагора BC = . Прямой подстановкой убеждаемся в справедливости ранее полученной формулы для длины медианы треугольника.
Задача для самостоятельного решения №2. В треугольнике ABC медианы, проведенные к сторонам AC и BC, пересекаются под прямым углом. Известно, что AC = b, BC = a. Найдите длину стороны AB.
Показать ответОтвет:Теорема о длине биссектрисы треугольника
Длина биссектрисы треугольника определяется по следующей формуле: где — биссектриса, проведенная к стороне — отрезки, на которые биссектриса делит сторону прилежащую к сторонам и соответственно. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.
| Пример 3. Дан треугольник со сторонами 4; 8; 9. Найти длину биссектрисы, проведенной к большей стороне.
|
Решение. Найдем сперва длины отрезков CL и LA. Используем для этого свойство биссектрисы треугольника. Биссектриса треугольника разбивает противоположную сторону на отрезки, пропорциональные прилежащим сторонам. То есть CL : CB = LA : BA или CL : 4 = LA : 8. Учитывая также, что CL + LA = 9, получаем, что CL = 3, LA = 6. По доказанной ранее теореме, длину биссектрисы BL можно найти по следующей формуле: BL2 = CB · BA — CL · LA = 4·8 — 3·6 = 14. Итак, BL =
Задача для самостоятельного решения №3. В треугольнике ABC сторона AB равна 21, биссектриса BD равна а отрезок DC равен 8. Найти периметр треугольника ABC.
Показать ответОтвет: 60.
Сергей ВалерьевичРепетитор по геометрии на Юго-Западной
yourtutor.info
Math.by - Длина биссектрисы треугольника
Длина биссектрисы :
ТеорияБиссектриса угла - это луч с началом в вершине угла, делящий угол на две равные части.
Биссектрисой треугольника называется отрезок бессектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Длина биссектрисы треугольника, проведенная из вершины B, вычисляется по следующей формуле:
,где p - полупериметр:
Аналогично получаем формулу биссектрисы проведенной из вершины A:
и для биссектрисы проведенной из вершины C:
Свойства биссектрис треугольника:
- биссектриса угла - это геометрическое место точек, равноудаленных от сторон этого угла;
- биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам;
- точка пересечений биссектрис треугольника является окружности, вписанной в этот треугольник.
www.math.by
Формулы для треугольника, как найти сторону, биссектрису, медиану, высоту, угол
Формулы для треугольника, как найти сторону, биссектрису, медиану, высоту, угол...
Найти длину биссектрисы в треугольнике
L - биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b - стороны треугольника
с - сторона на которую опущена биссектриса
d, e - отрезки полученные делением биссектрисы
γ - угол ABC, разделенный биссектрисой пополам
p - полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
Биссектриса прямоугольного треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L - биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b - катеты прямоугольного треугольника
с - гипотенуза
α - угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L - биссектриса, отрезок ME , исходящий из острого угла
a, b - катеты прямоугольного треугольника
с - гипотенуза
α, β - углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
Длина биссектрисы равнобедренного треугольника
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L - высота=биссектриса=медиана
a - одинаковые стороны треугольника
b - основание
α - равные углы при основании
β - угол вершины
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Найти медиану=биссектрису=высоту равностороннего треугольника
Формула для вычисления высоты= биссектрисы= медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L - высота=биссектриса=медиана
a - стороны треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Найти длину медианы треугольника по формулам
Медиана - отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам. Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M - медиана, отрезок |AO|
c - сторона на которую ложится медиана
a , b - стороны треугольника
γ - угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Длина медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам. Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M - медиана
R - радиус описанной окружности
O - центр описанной окружности
с - гипотенуза
a, b - катеты
α - острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Найти длину высоты треугольника
Высота- перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом). Высоты треугольника пересекаются в одной точке, которая называется - ортоцентр.
H - высота треугольника
a - сторона, основание
b. c - стороны
β, γ - углы при основании
p - полупериметр, p=(a+b+c)/2
R - радиус описанной окружности
S - площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
Формулы высоты прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр - точка пересечения высот, совпадает с вершиной прямого угла.
H - высота из прямого угла
a, b - катеты
с - гипотенуза
c1 , c2 - отрезки полученные от деления гипотенузы, высотой
α, β - углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c - стороны произвольного треугольника
α, β, γ - противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
*Внимательно, при подстановке в формулу, для тупого угла ( α>90),сosα, принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b - сторона (основание)
a - равные стороны
α - углы при основании
β - угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a, b - катеты
c - гипотенуза
α, β - острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (c, a, b):
ifreestore.net
Все формулы биссектрисы прямоугольного треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L - биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b - катеты прямоугольного треугольника
с - гипотенуза
α - угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L - биссектриса, отрезок ME , исходящий из острого угла
a, b - катеты прямоугольного треугольника
с - гипотенуза
α, β - углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
Подробности Автор: Administrator Опубликовано: 07 октября 2011 Обновлено: 16 мая 2017
www-formula.ru
