Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы. Найти матрицы методом присоединенной матрицы
Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если выполняется условие: АА-1= А-1А=Е, где Е - единичная матрица того же порядка, что и матрица А. Обратная А-1матрица имеет ту же размерность, что и матрица А.
Определение. Квадратная матрица А= называется невырожденной, если её определитель неравен нулю, в противном случае матрица называется вырожденной.
называется невырожденной, если её определитель неравен нулю, в противном случае матрица называется вырожденной.
Теорема.Всякая невырожденная матрица имеет обратную.
Определение. Присоединенной матрицей к матрице А называется матрица вида:
к матрице А называется матрица вида:
 =
= , где Аij-алгебраическое дополнение элемента аij.
, где Аij-алгебраическое дополнение элемента аij.
Находят обратную матрицу поформуле: А-1=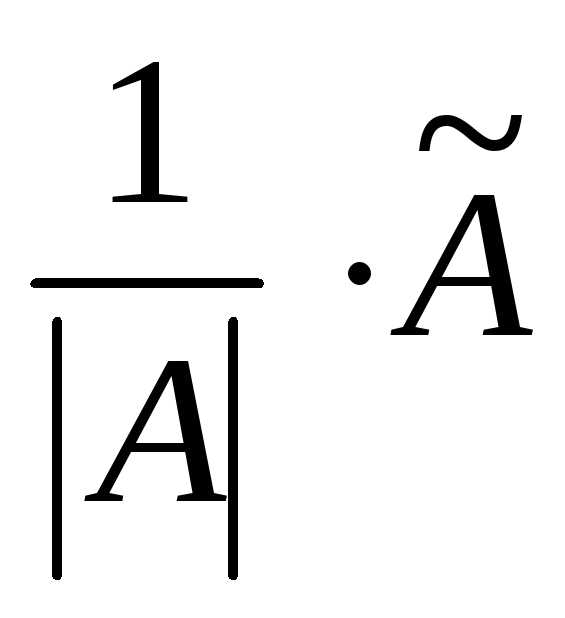 .
.
Пример 3.1
Найти обратную матрицу методом присоединенной матрицы.
А=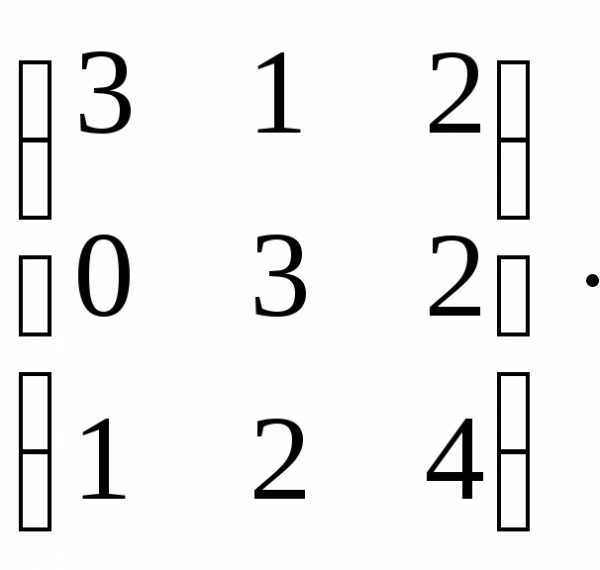
Решение.
Выясним, является ли данная матрица невырожденной. Для этого найдем определитель матрицы:
 =3(-1)1+1
=3(-1)1+1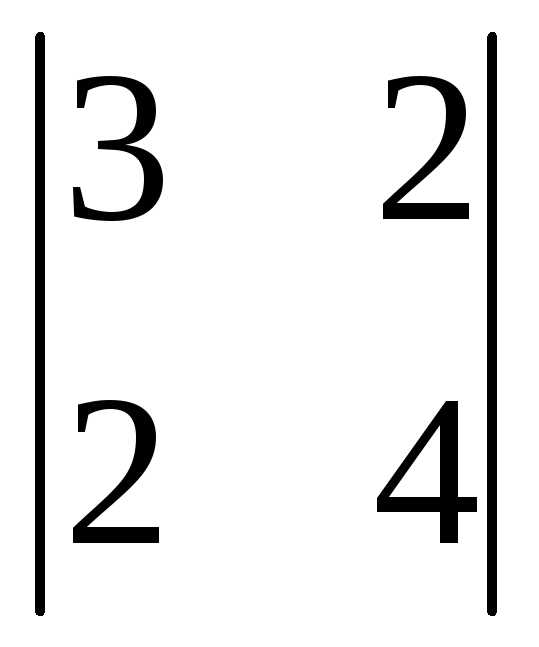 +0(-1)2+1
+0(-1)2+1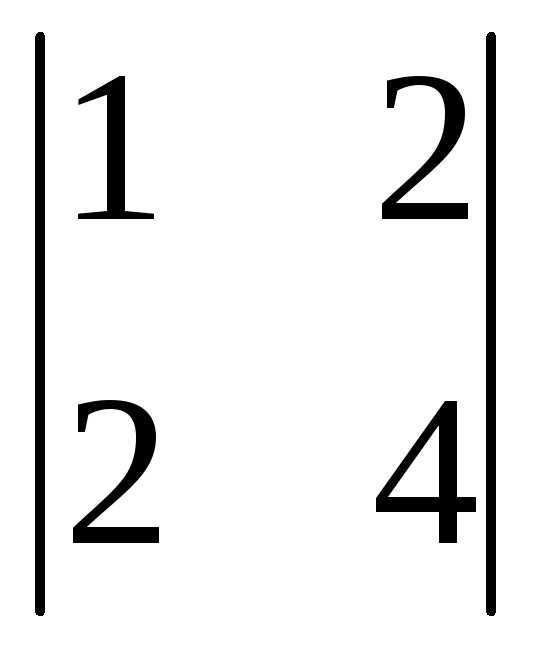 +1(-1)3+1
+1(-1)3+1 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к. 
Найдем транспонированную матрицу.
АТ=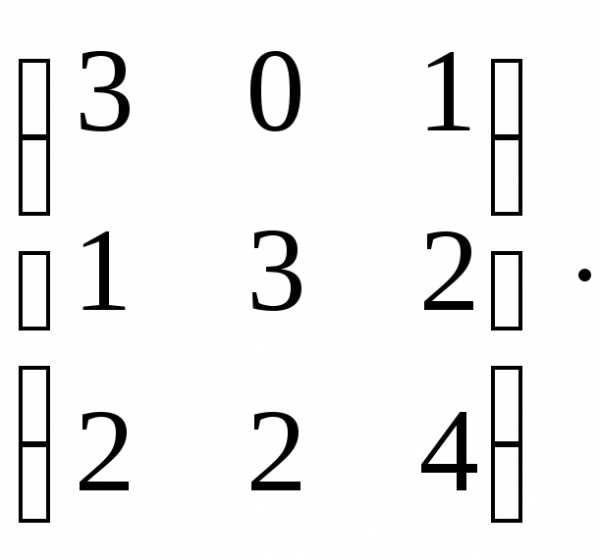
Вычислим присоединенную матрицу. Для этого найдем алгебраическое дополнение каждого элемента матрицы.
 = (-1)1+1
= (-1)1+1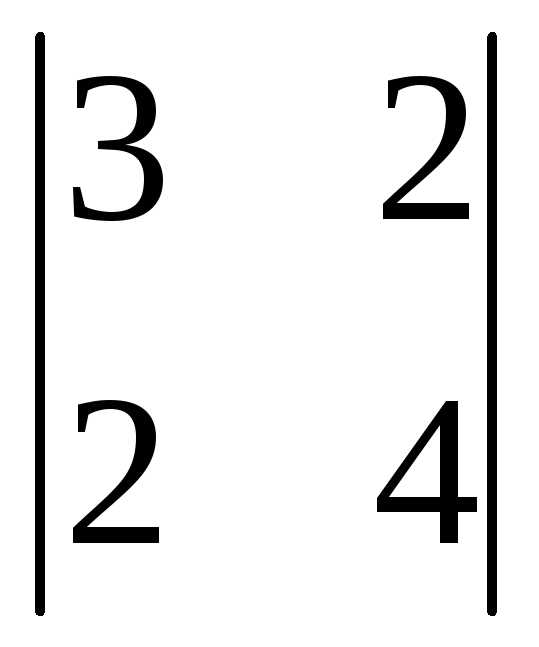 =12-4=8
=12-4=8
 = (-1)1+2
= (-1)1+2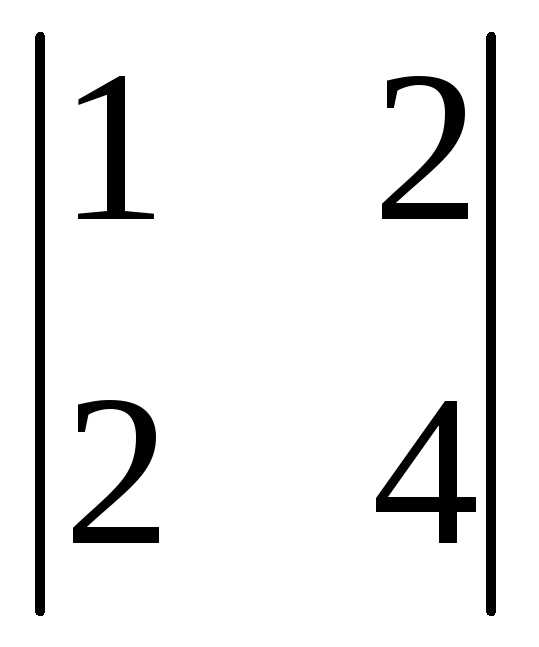 = -(4-4)= 0
= -(4-4)= 0
 = (-1)1+3
= (-1)1+3 = 2-6= -4
= 2-6= -4
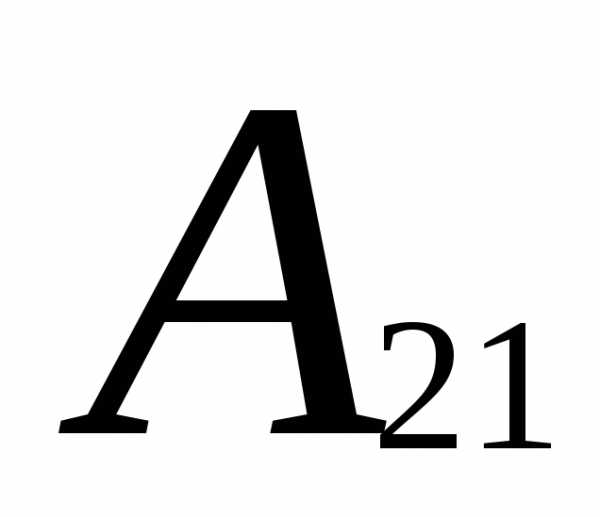 = (-1)2+1
= (-1)2+1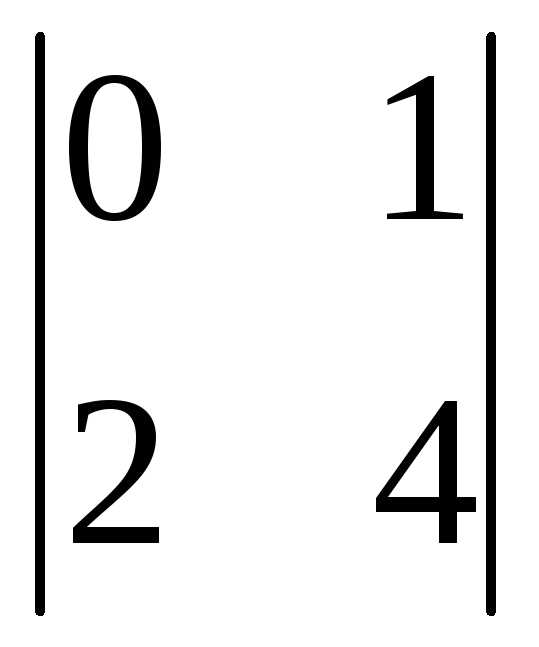 = -(0-2)=2
= -(0-2)=2
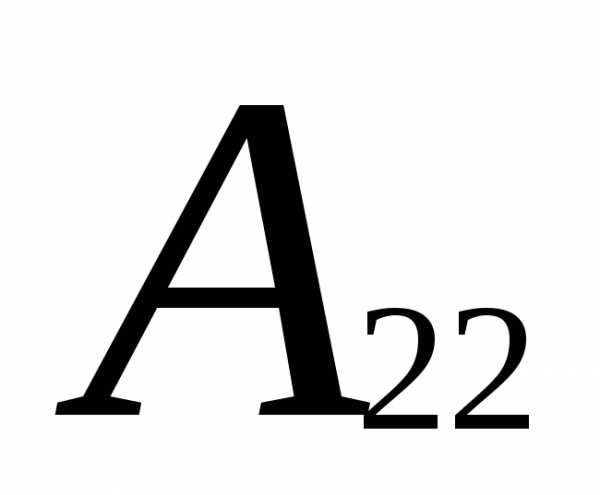
 = 12-2=10
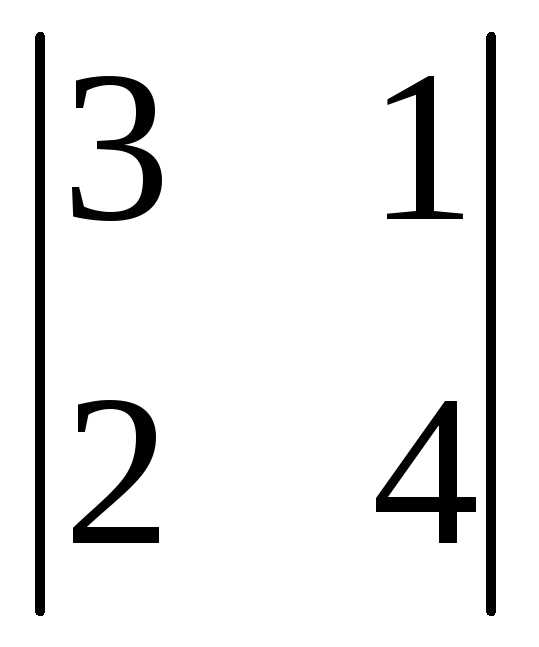
= 12-2=10  = (-1)2+3
= (-1)2+3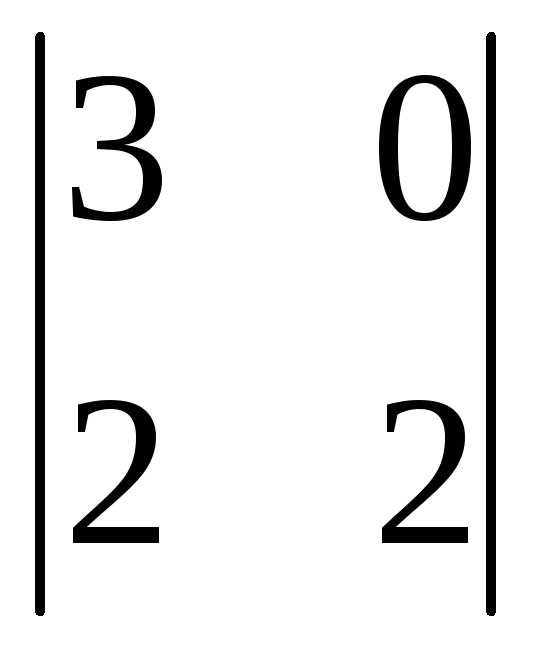 = -(6-0)= -6
= -(6-0)= -6
 = (-1)3+1
= (-1)3+1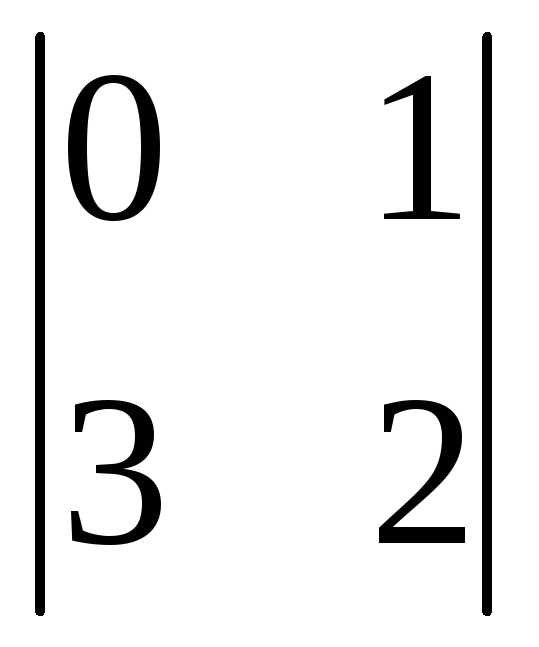 = 0-3= -3
= 0-3= -3
 = (-1)3+2
= (-1)3+2 = -(6-1)= -5
= -(6-1)= -5
 = (-1)3+3= 9-0=9.
= (-1)3+3= 9-0=9.
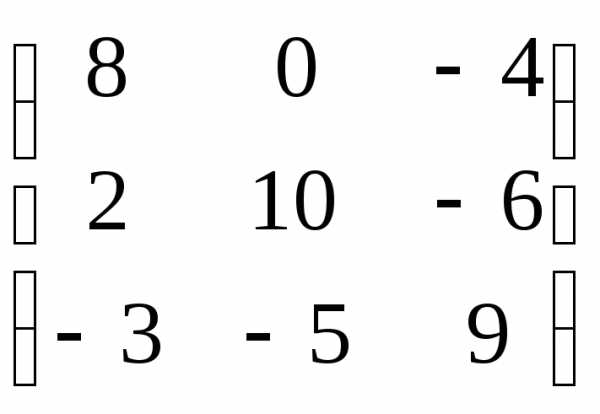
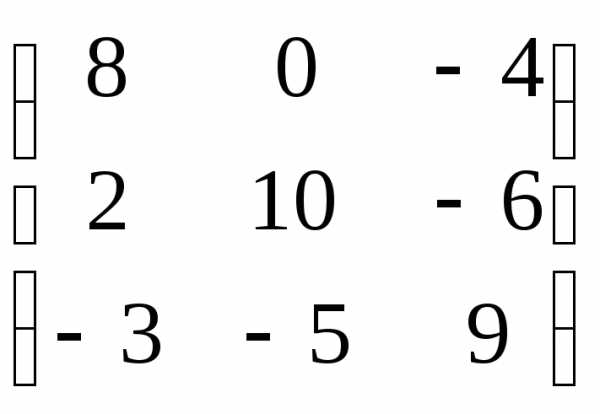
 =
=
4. Воспользуемся формулой: А-1=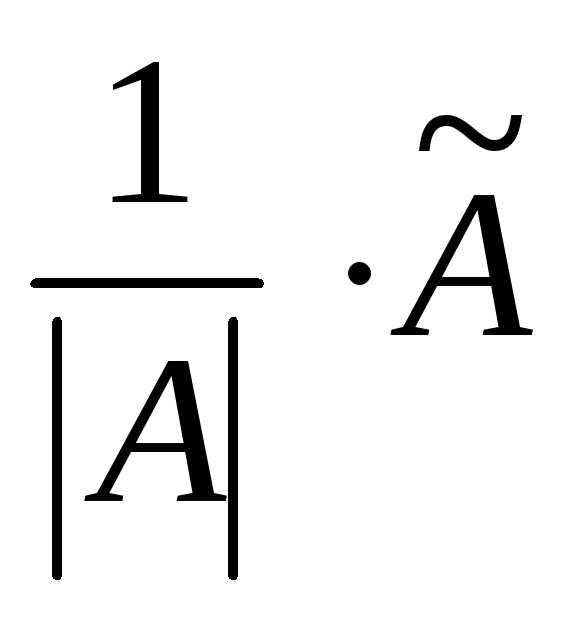 .
.
А-1=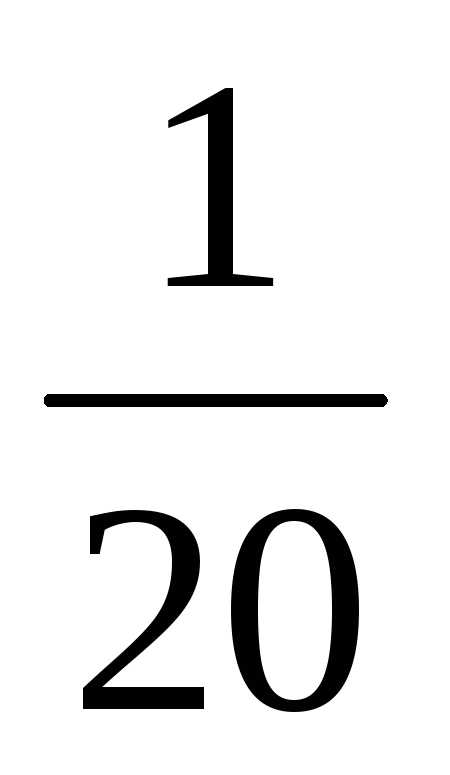
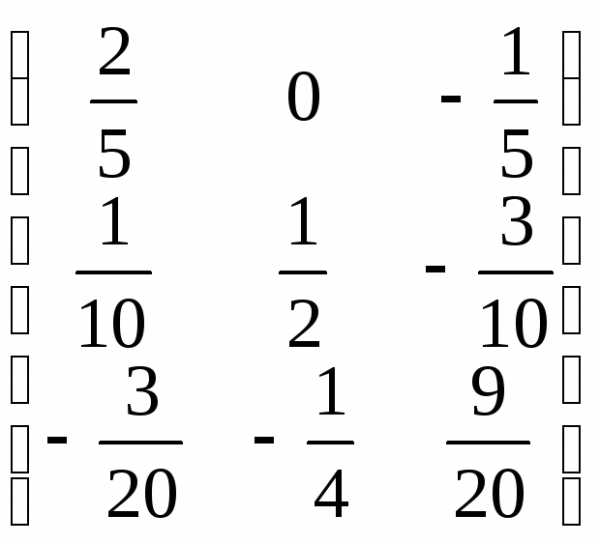 .
.Решение систем линейных уравнений методом обратной матрицы
Пусть дана система линейных уравнений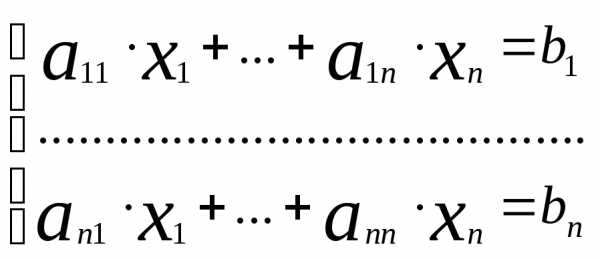 . Обозначим её через (1). Выпишим основную матрицу данной системы: А=
. Обозначим её через (1). Выпишим основную матрицу данной системы: А= , вектор-столбец неизвестных:X=
, вектор-столбец неизвестных:X=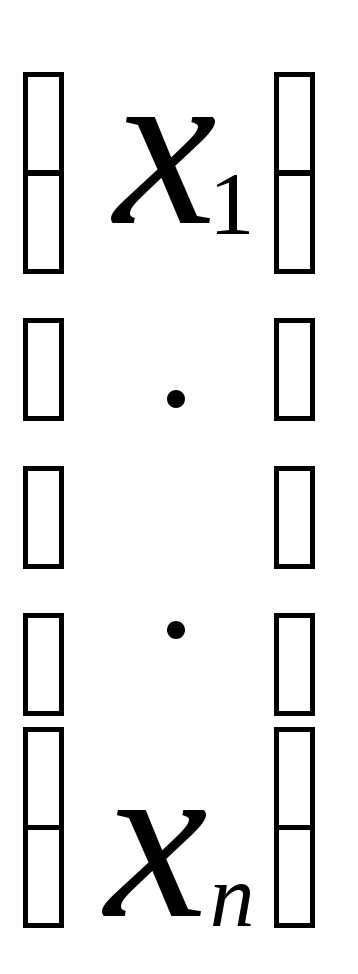 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B= . Теперь перепишем систему (1) в матричной форме:AX=B
. Теперь перепишем систему (1) в матричной форме:AX=B X=A-1B- решение системы (1).
X=A-1B- решение системы (1).
Пример 3.2
Решить систему линейных уравнений: 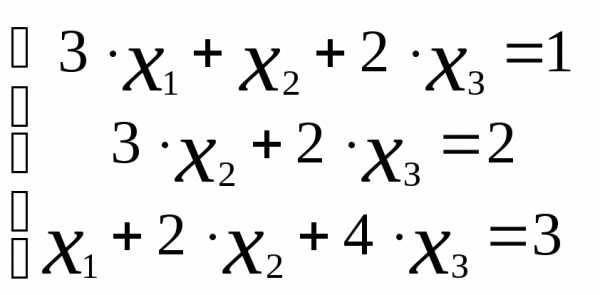 методом обратной матрицы.
методом обратной матрицы.
Решение.
Формула, по которой будем находить решение системы: X=A-1B.
Основная матрица системы А=
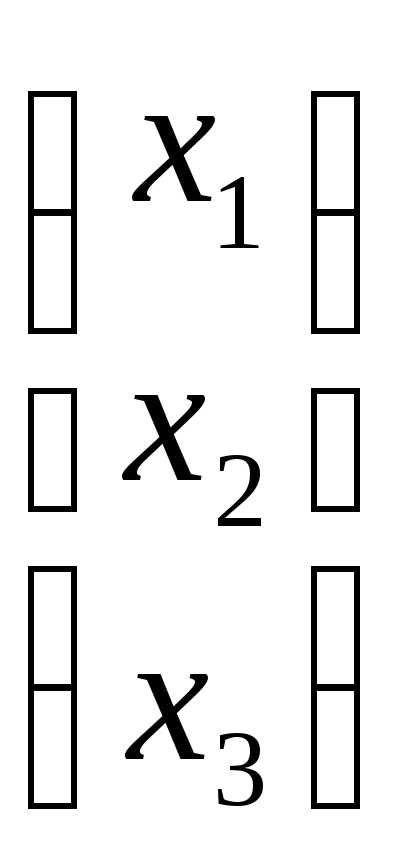
 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=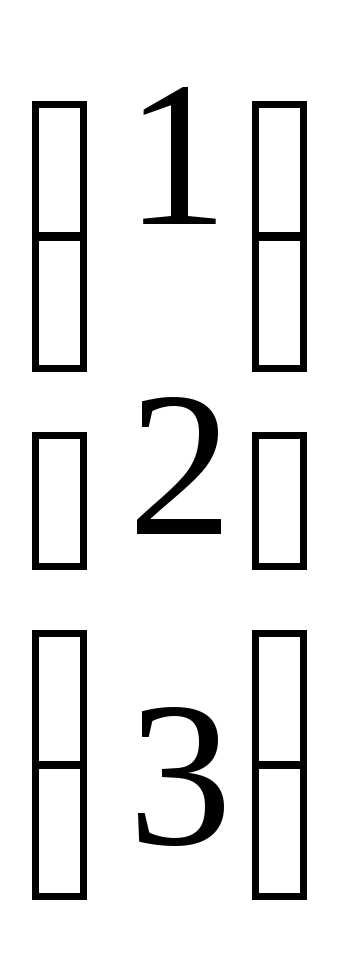 .
. Найдем определитель  =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1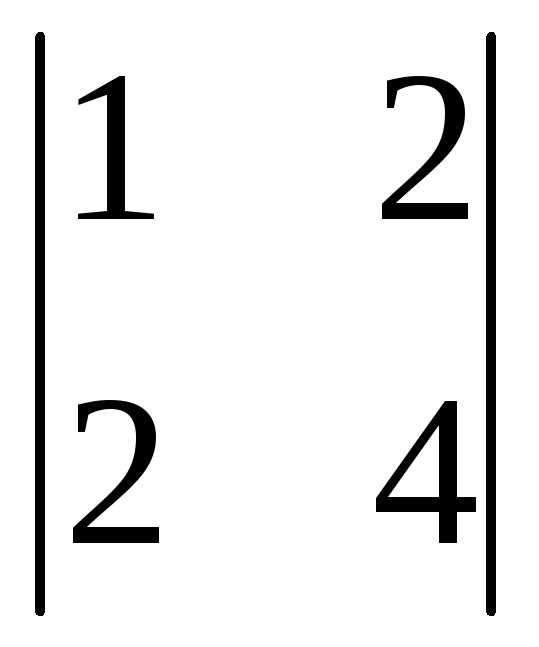 +1(-1)3+1
+1(-1)3+1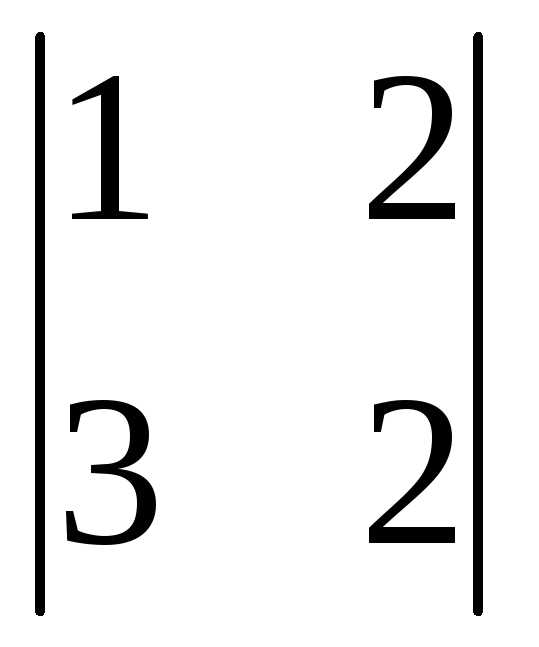 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0, следовательно, данная матрица имеет обратную.
0, следовательно, данная матрица имеет обратную.
Найдем обратную матрицу с помощью присоединенной матрицы (см. пример 3.1):
А-1=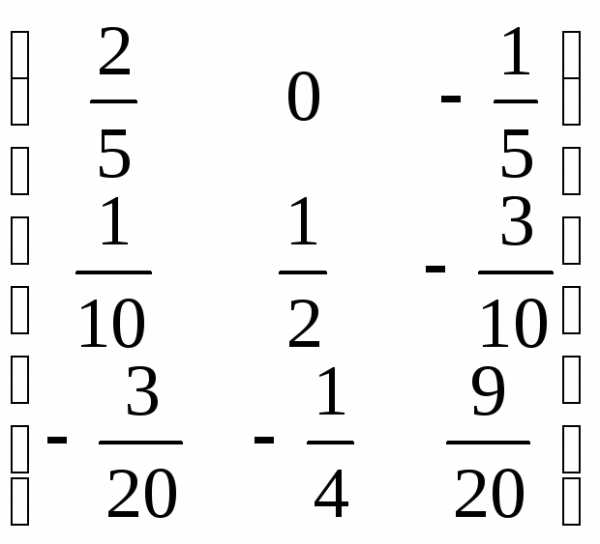 .
.
Подставим в формулу X=A-1B, получим:X=
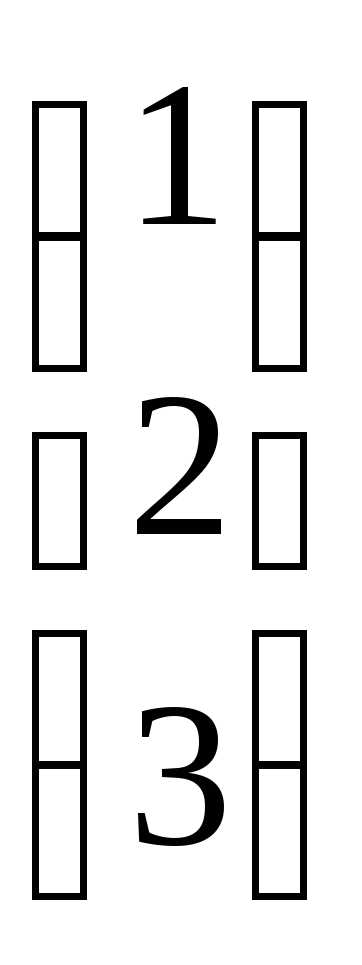
 =
=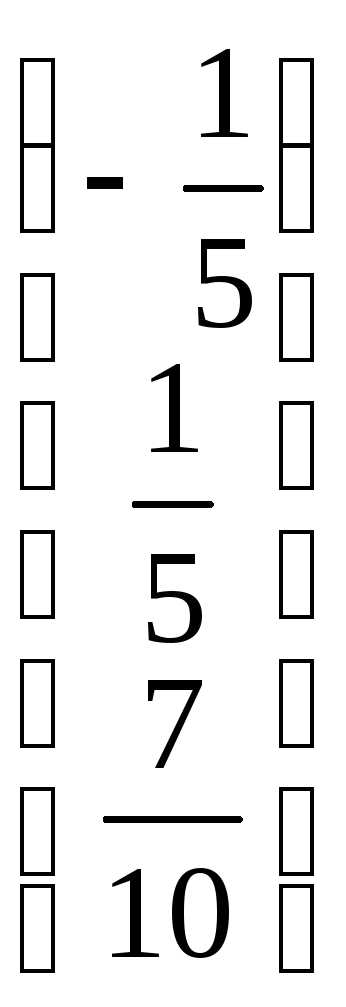
Ответ:  =
=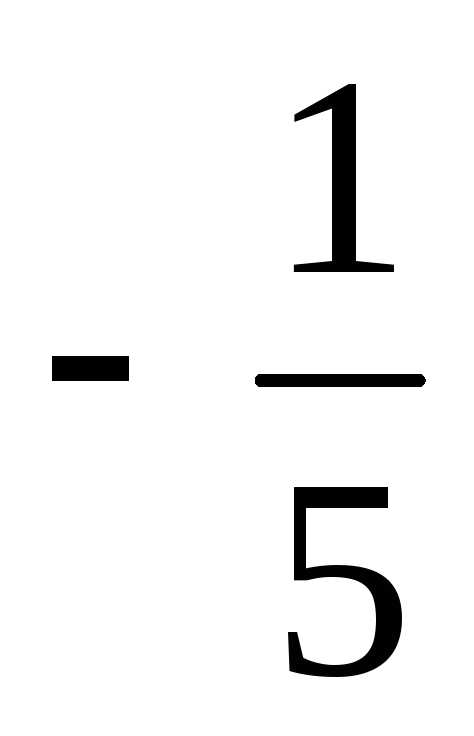 ,
, 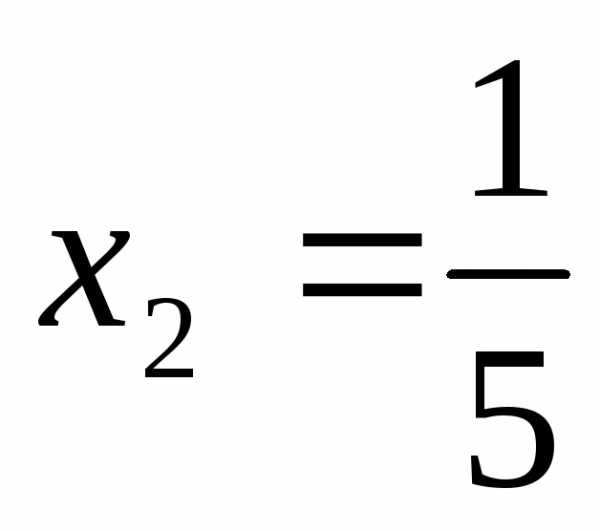 ,
,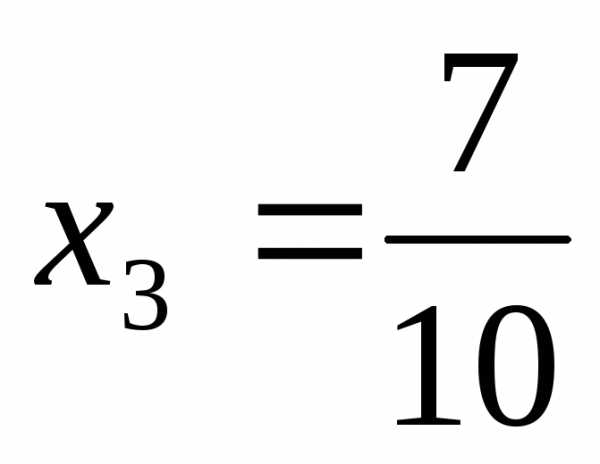 .
.
Правильность решения легко проверить, подставив полученные результаты ,
, 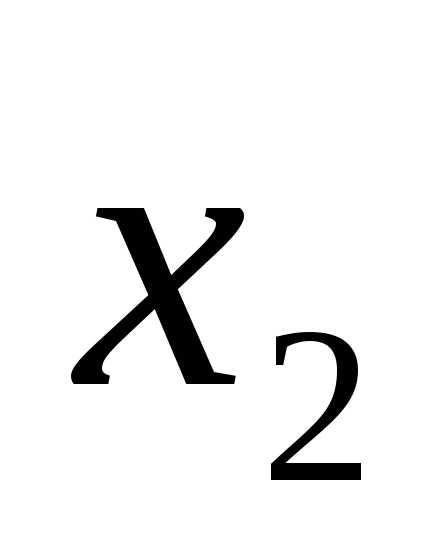 ,
, 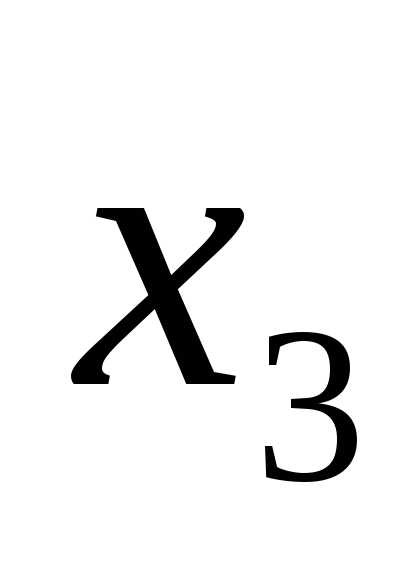 в данную систему уравнения.
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений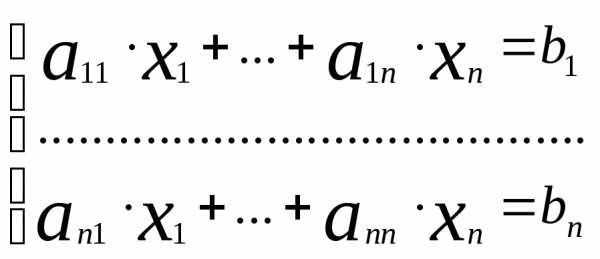 . Обозначим её через (1). Основная матрица данной системы: А=
. Обозначим её через (1). Основная матрица данной системы: А=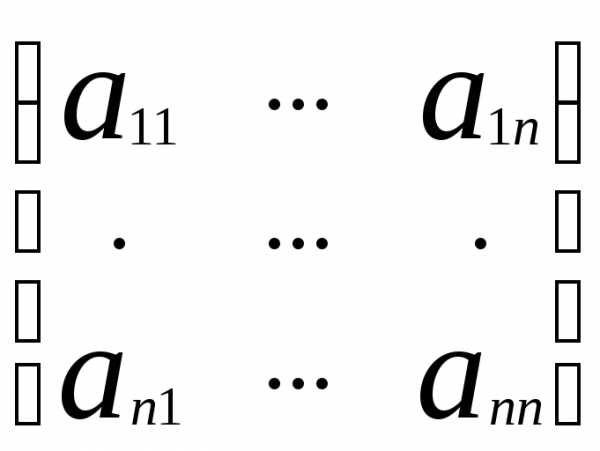 , вектор-столбец неизвестных:X=
, вектор-столбец неизвестных:X=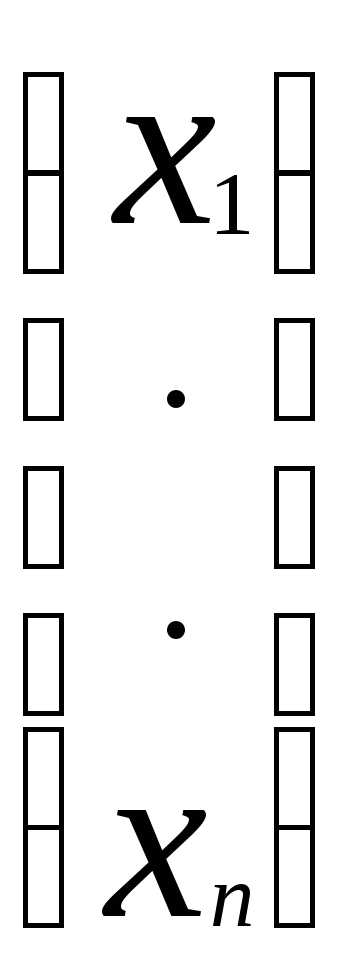
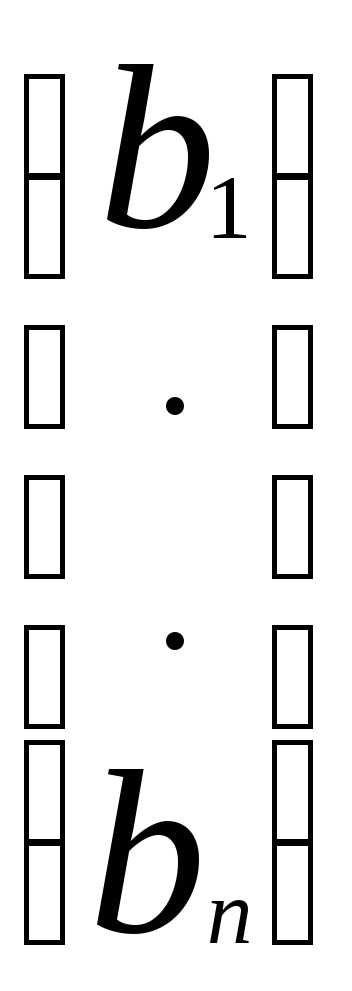 . Теперь запишем систему (1) в матричной форме:AX=B.
. Теперь запишем систему (1) в матричной форме:AX=B. Теорема Крамера. Пусть  -определитель матрицы А,
-определитель матрицы А,  j-определитель матрицы, получаемой из А заменойj-го столбца столбцом свободных членов. Тогда, если
j-определитель матрицы, получаемой из А заменойj-го столбца столбцом свободных членов. Тогда, если
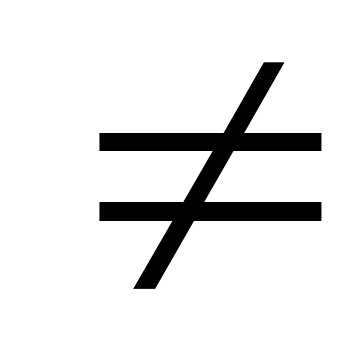 0, то система имеет единственное решение:
0, то система имеет единственное решение: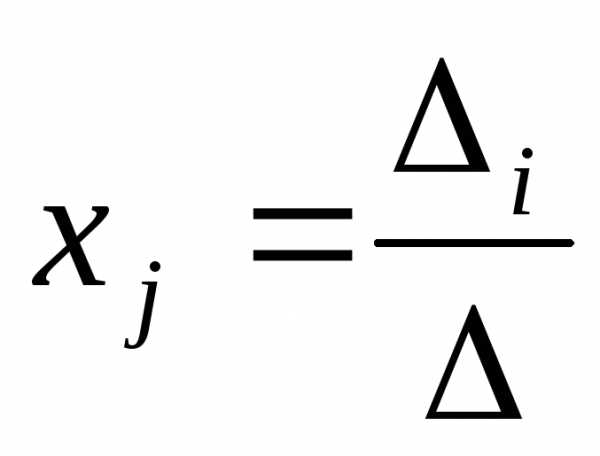 , (1jn).
, (1jn).
Пример 4.1
Решить систему линейных уравнений: 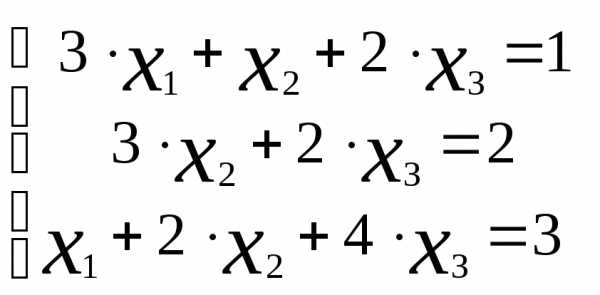 методом Крамера.
методом Крамера.
Решение.
Основная матрица системы А=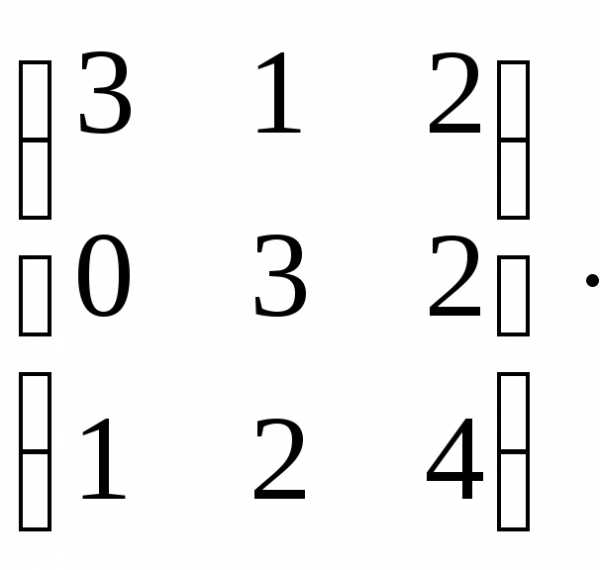 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=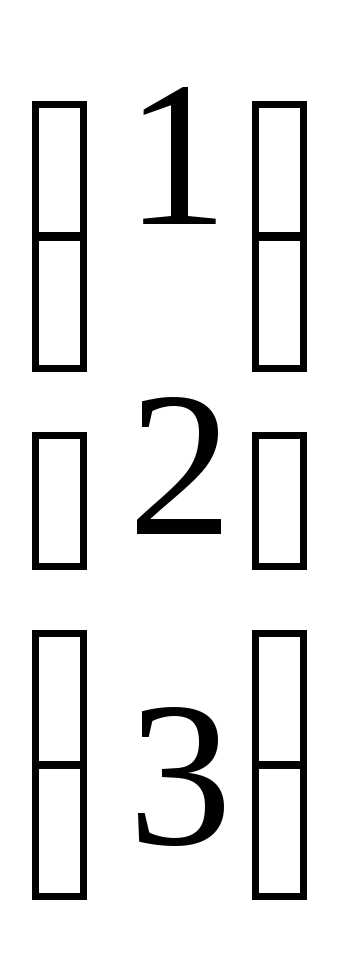
Найдем определитель  =
= =3(-1)1+1
=3(-1)1+1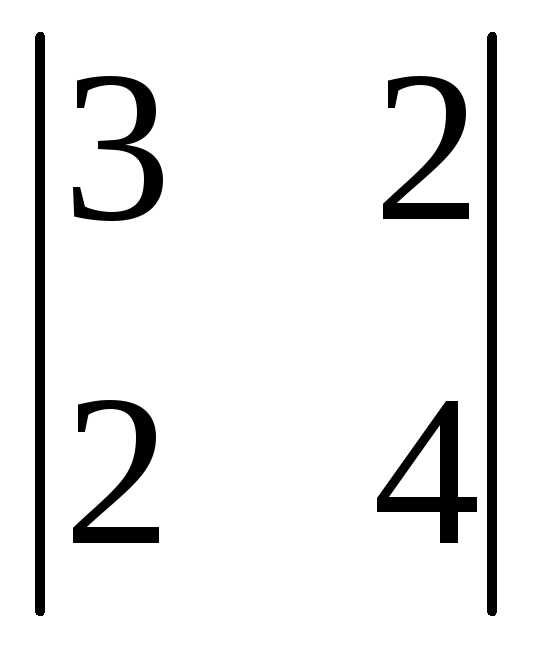 +0(-1)2+1
+0(-1)2+1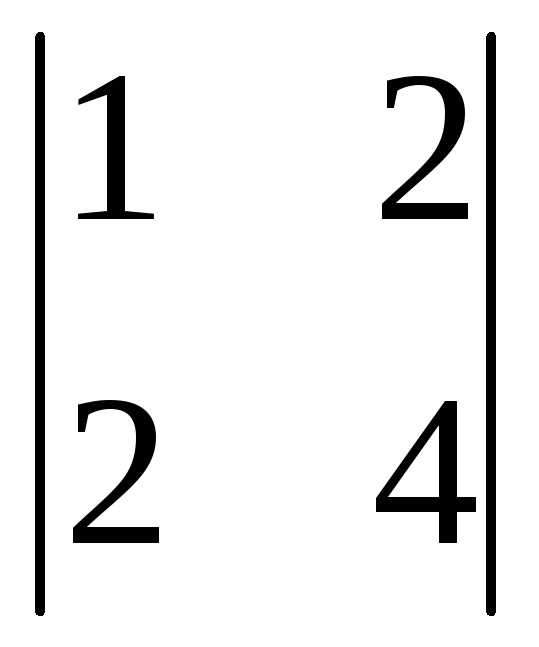 +1(-1)3+1
+1(-1)3+1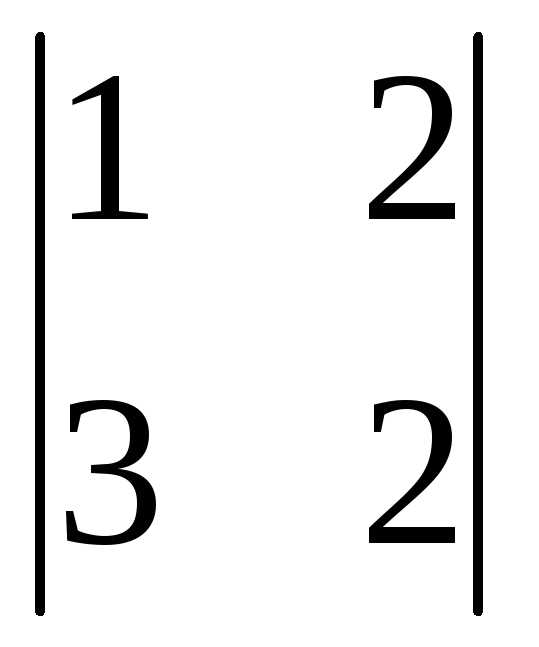 =3(12-4)+0+(2-6)=24-4=20. Т.к.
=3(12-4)+0+(2-6)=24-4=20. Т.к. 0, следовательно, можно применить формулы Крамера.
0, следовательно, можно применить формулы Крамера.
Найдем определители 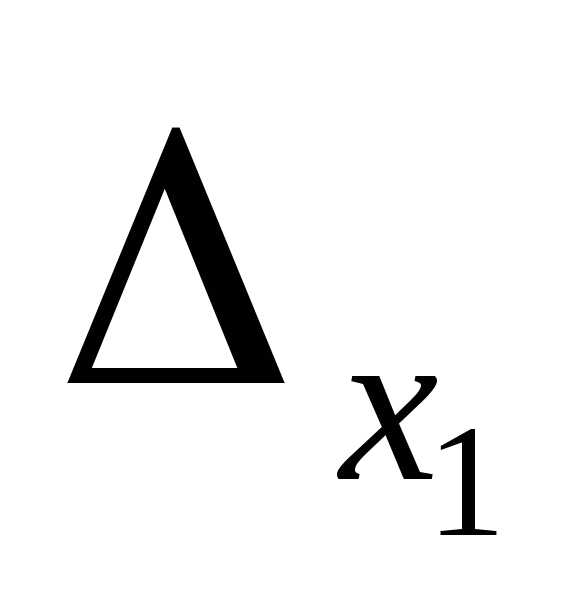 ,
,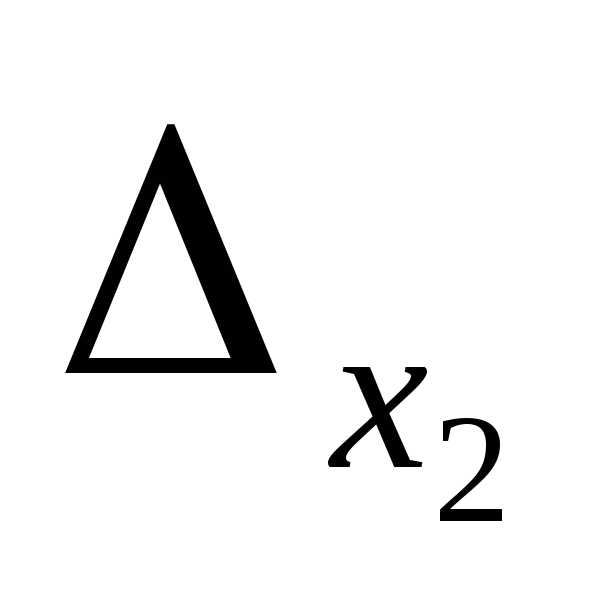 ,
,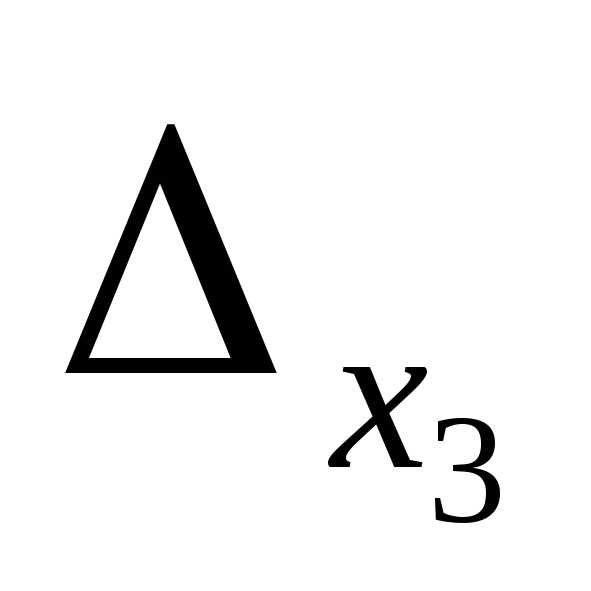 , полученные заменой соответствующих столбцов столбцом свободных членов:
, полученные заменой соответствующих столбцов столбцом свободных членов:
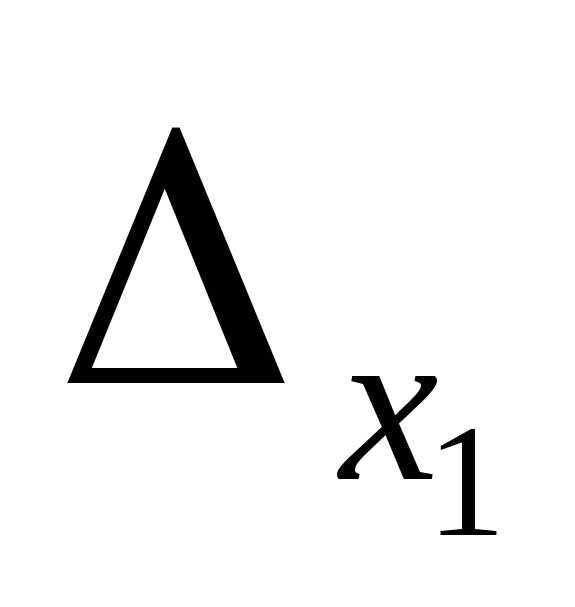 =
=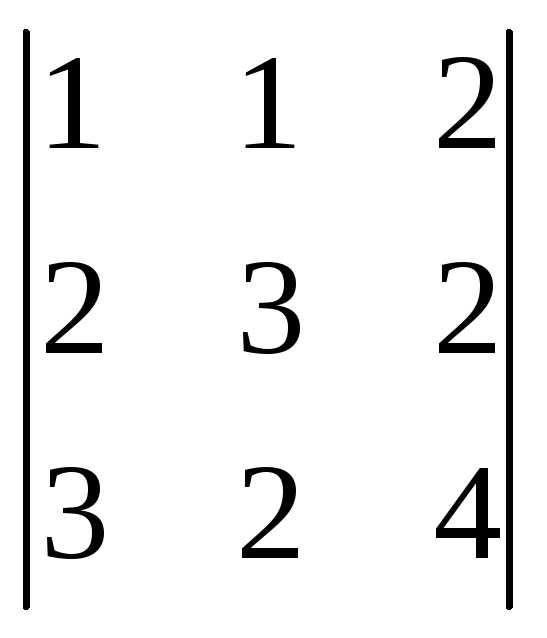 =1(12-4)-1(8-6)+2(4-9)=8-2-10= -4;
=1(12-4)-1(8-6)+2(4-9)=8-2-10= -4;
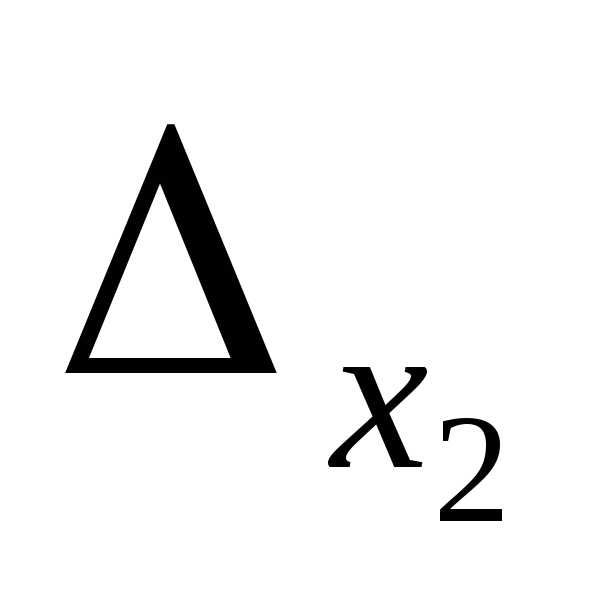
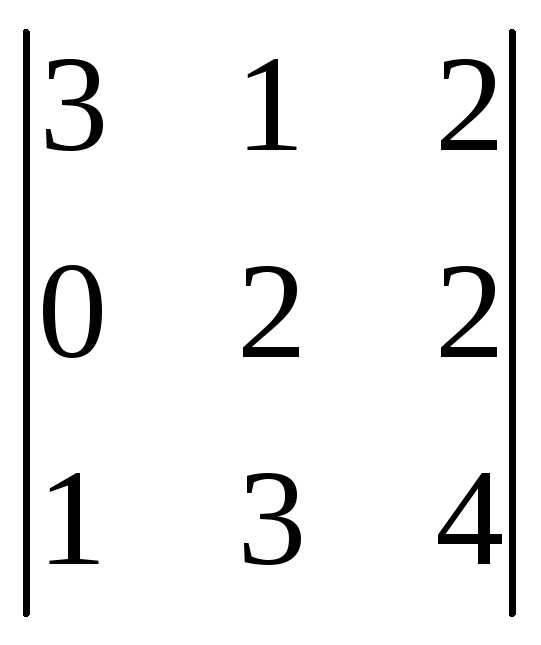 =3(8-6)-0+1(2-4)=6-2=4;
=3(8-6)-0+1(2-4)=6-2=4; 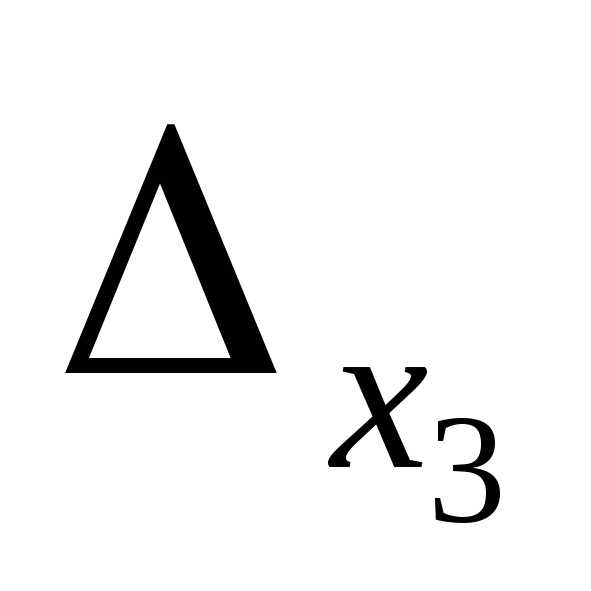 =
= =3(9-4)-0+1(2-3)=15-1=14.
=3(9-4)-0+1(2-3)=15-1=14.
Тогда, по формуле Крамера:
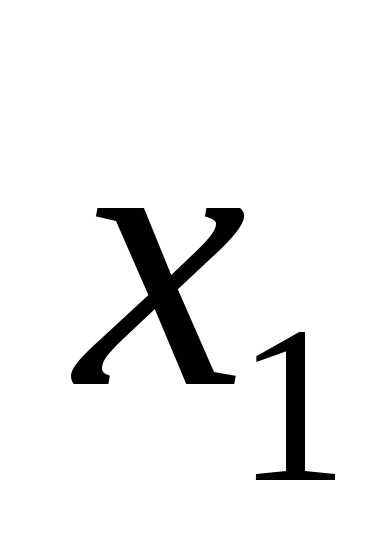 =
=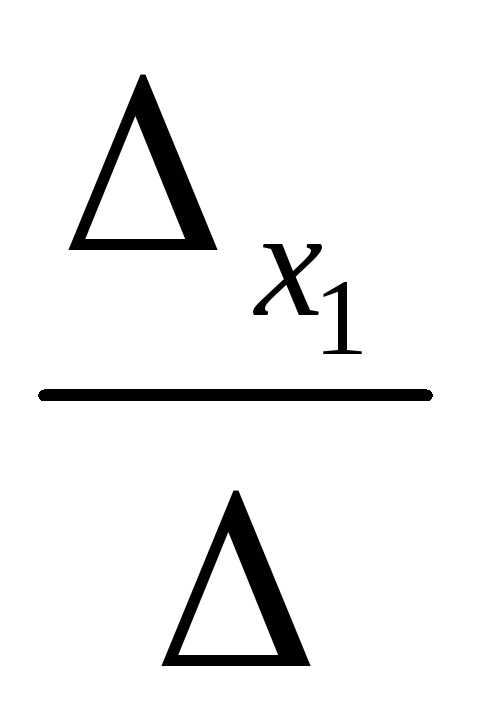 = -
= -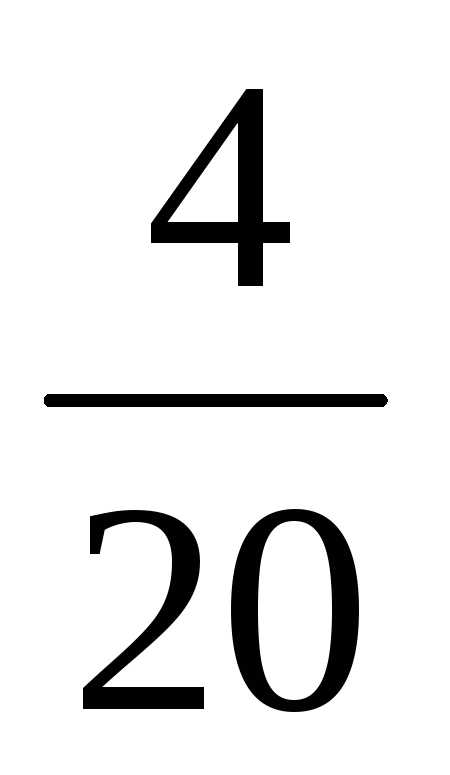 =
=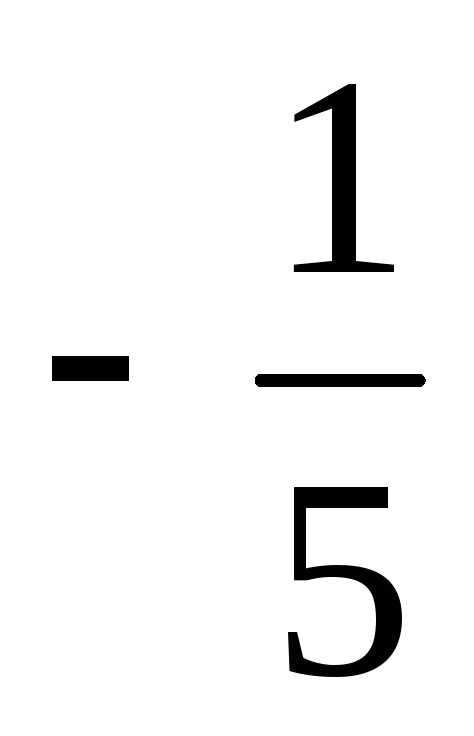 ;
;
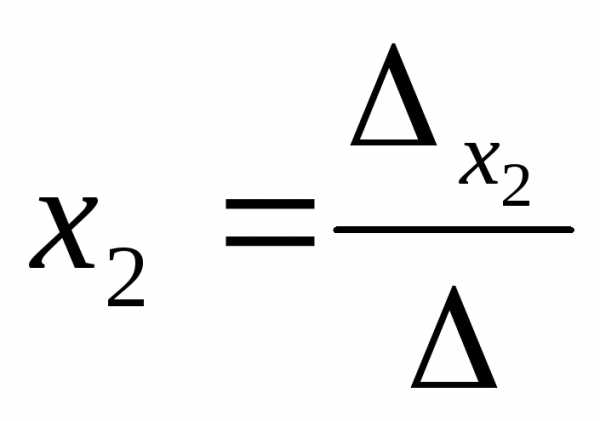 =
= ;
;
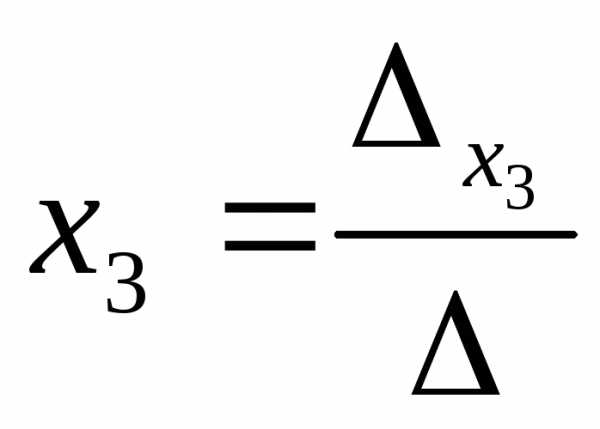 =
=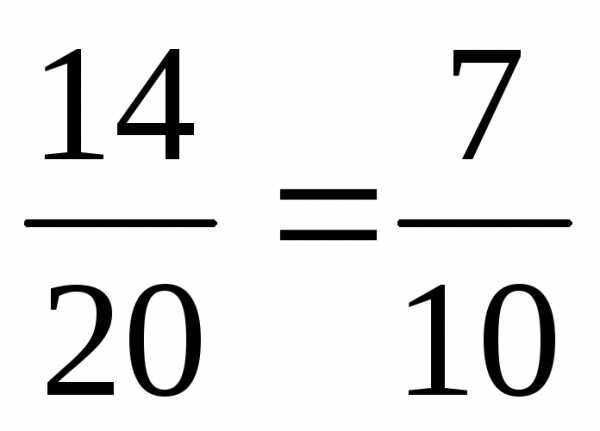 .
.
Ответ: 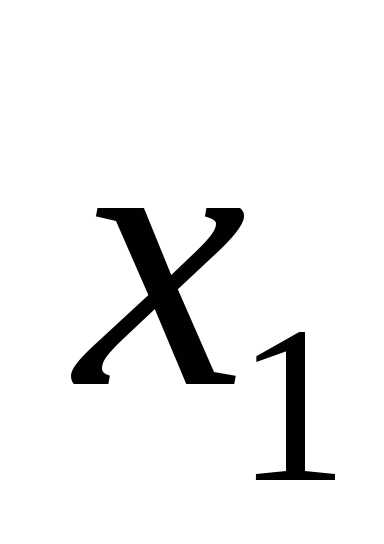 =
=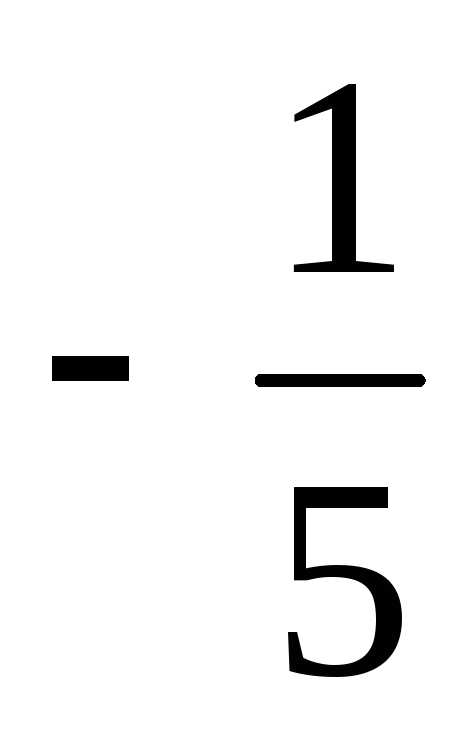 ,
, 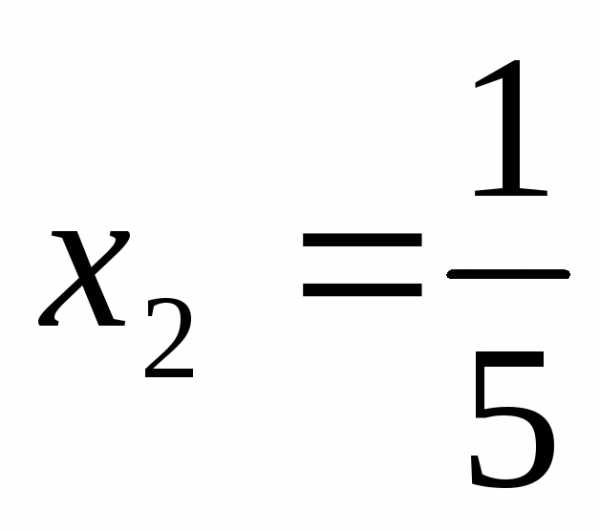
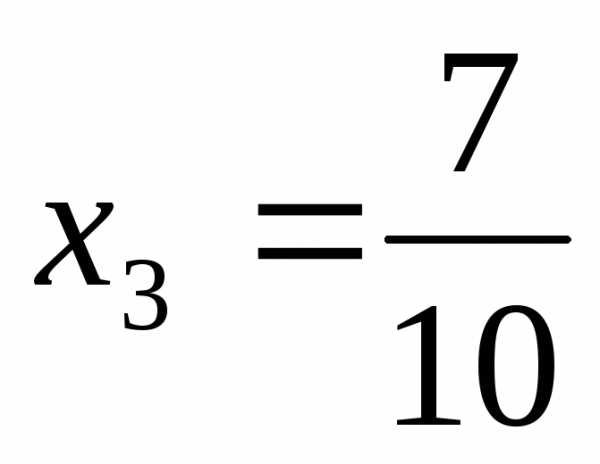 .
.Решение систем линейных уравнений методом Гаусса
Пусть дана система линейных уравнений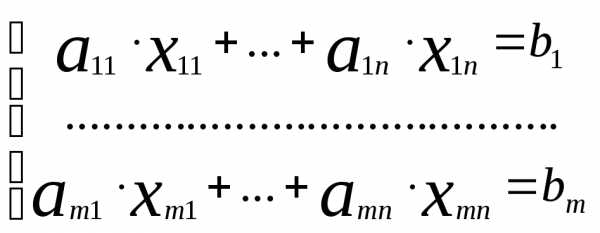 . Рассмотрим расширенную матрицу (АВ) данной системы и с помощью элементарных преобразований приведем её к ступенчатому виду, в результате получим расширенную матрицу (АВ).
. Рассмотрим расширенную матрицу (АВ) данной системы и с помощью элементарных преобразований приведем её к ступенчатому виду, в результате получим расширенную матрицу (АВ).
Если ранг основной матрицы системы меньше ранга расширенной матрицы r(A)<r(АВ), то система несовместна. Еслиr(A)=r(АВ)=n, гдеn-число неизвестных, то система совместна и определена. Еслиr(A)=r(АВ)<n, гдеn-число неизвестных, то система совместна и неопределенна.
Записываем систему линейных уравнений из полученной ступенчатой матрицы. Определяем базисные и свободные переменные, и выражая базисные переменные через свободные получаем решение системы.
Пример 4.2
Решить систему линейных уравнений: 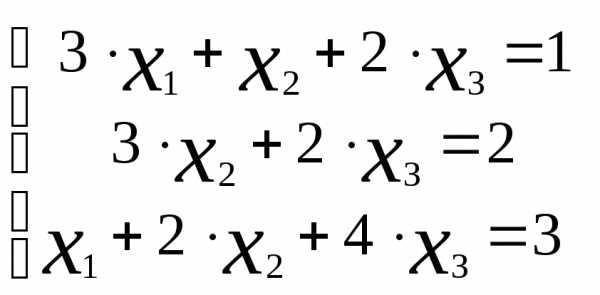 методом Гаусса.
методом Гаусса.
Решение.
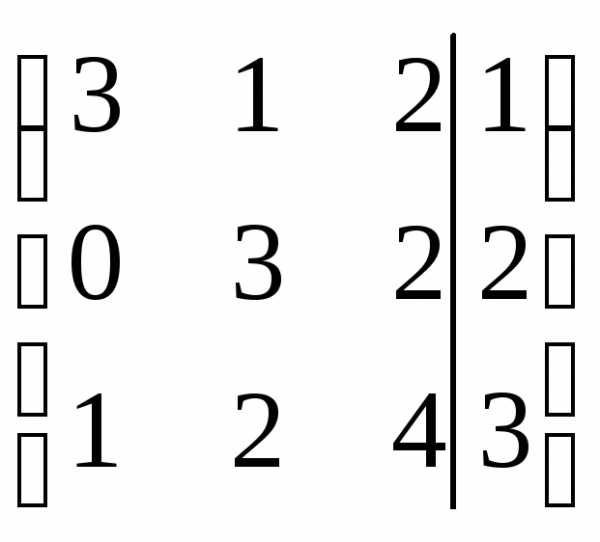

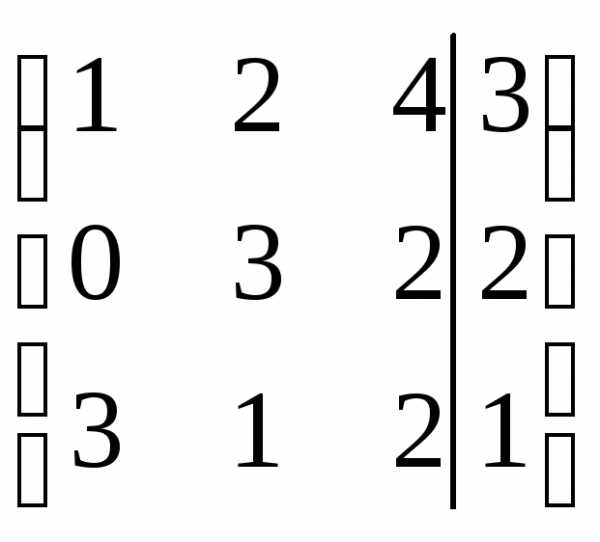
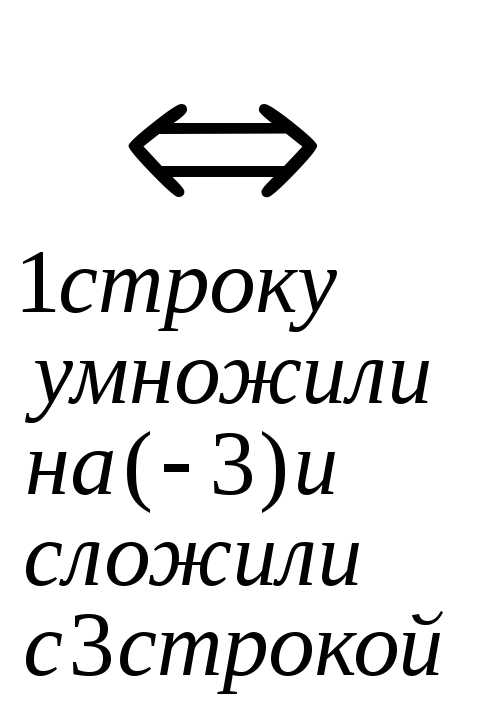
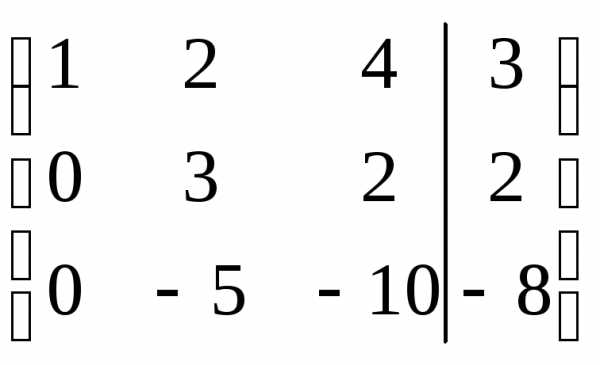

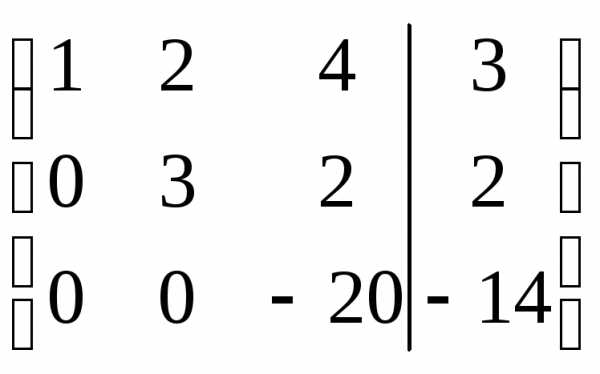
r(A)=r(АВ)=n система совместна и определена.
система совместна и определена.
Отсюда, запишем эквивалентную систему уравнений, имеем: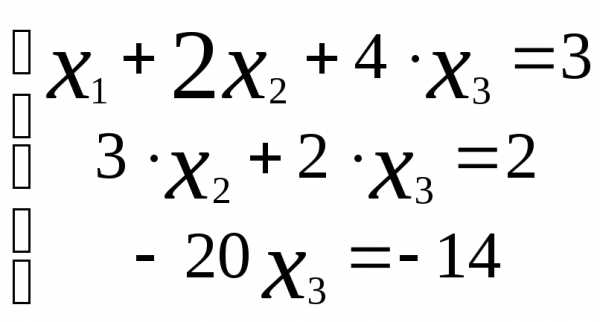
Решая её, получаем: 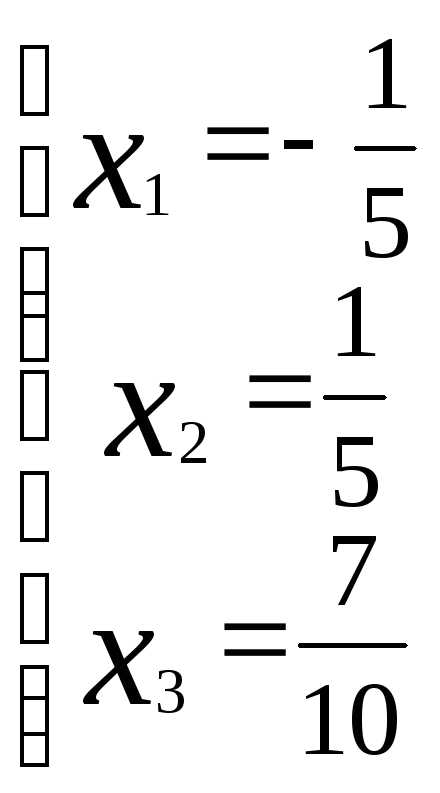
Ответ: 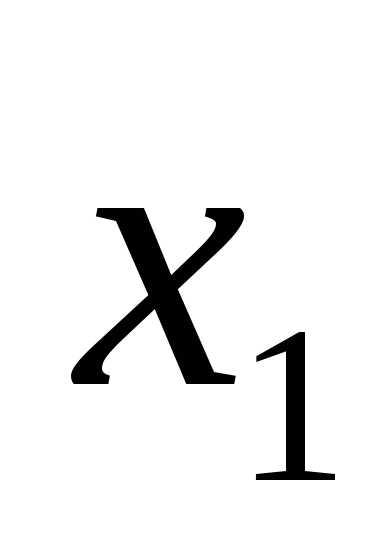 =
=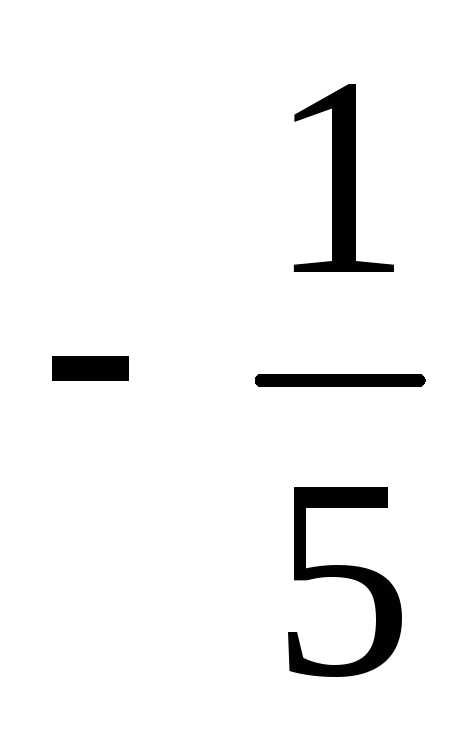 ,
, 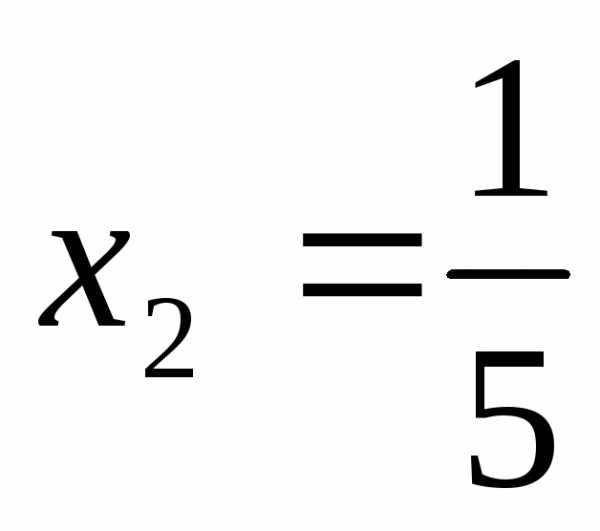 ,
,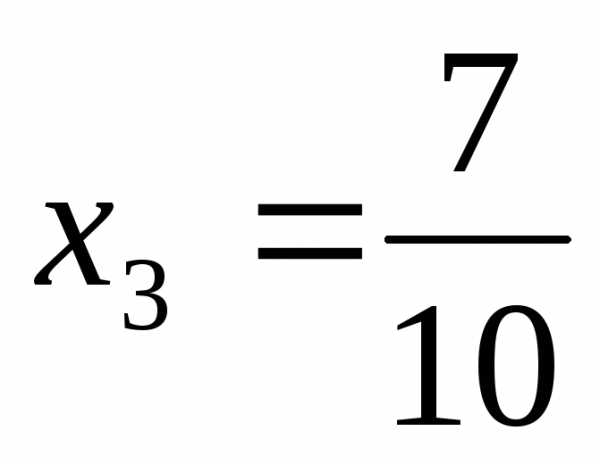 .
.
Пример 4.3
Найти общее решение системы: 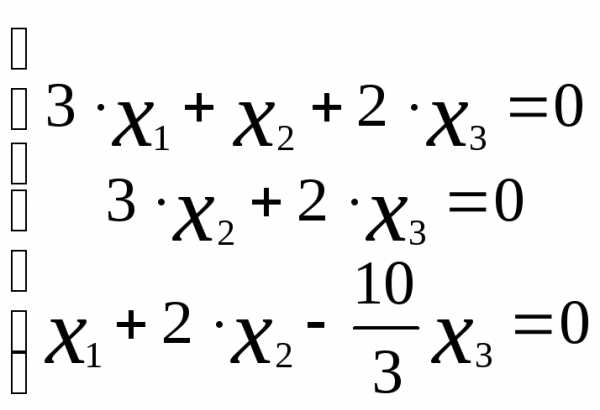 .
.
Решение.
Составим матрицу системы: А=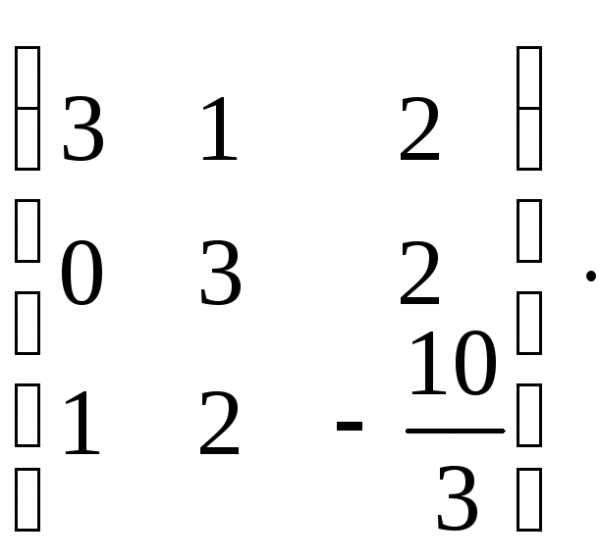
Приведем её к треугольному виду:
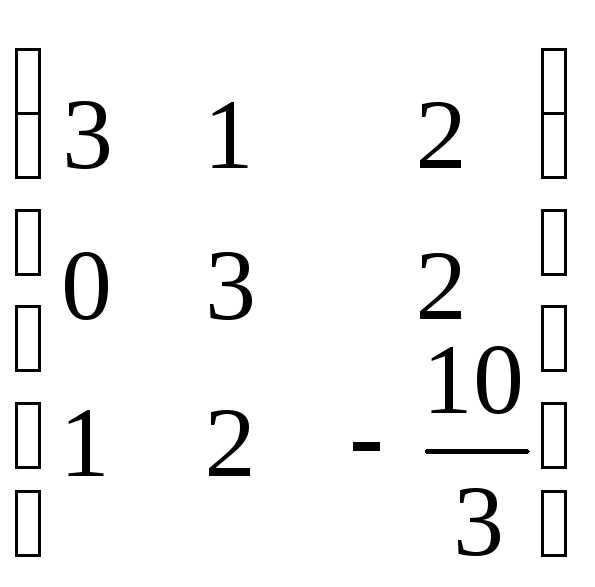

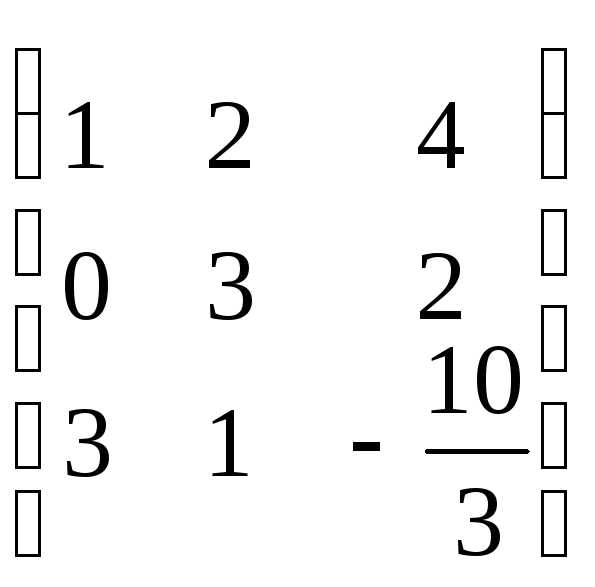
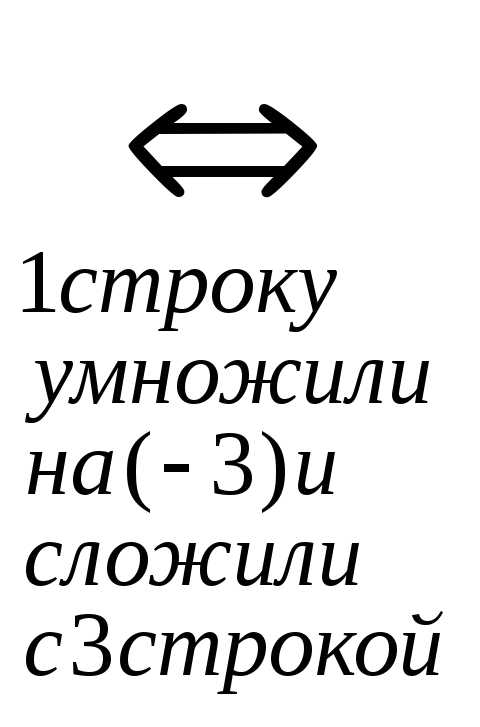
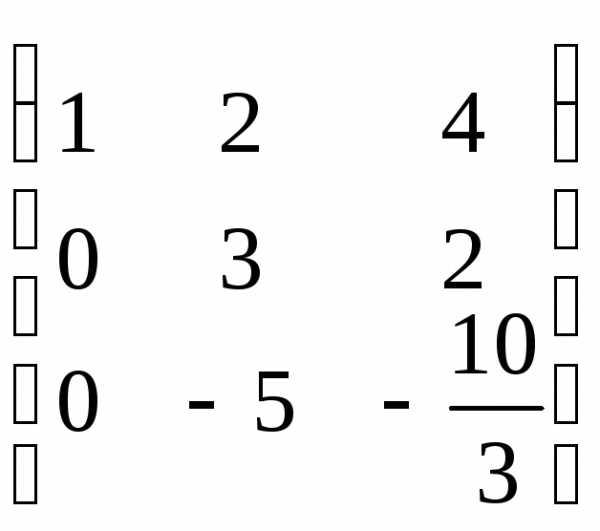
r(A)=2. Запишем эквивалентную систему уравнений: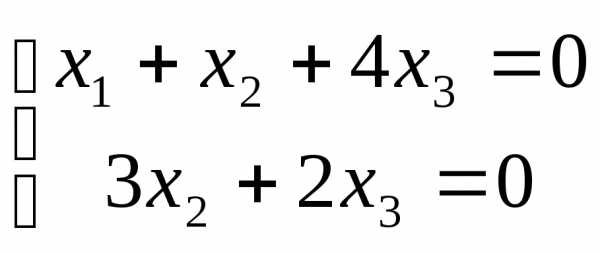
Примем за базисные переменные 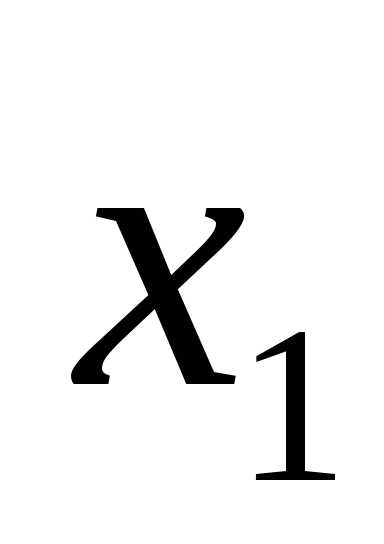 и
и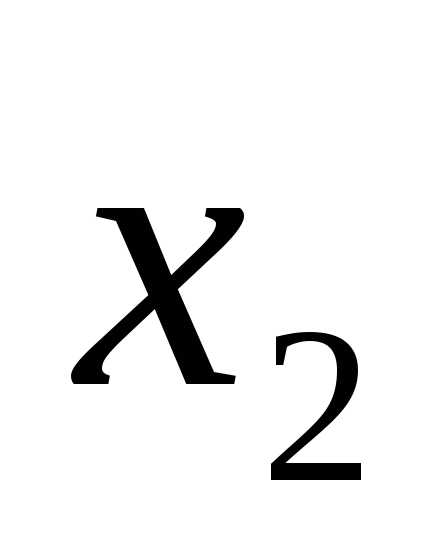 , а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (3-2)=1, т. е. у нас одна свободная переменная это
, а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (3-2)=1, т. е. у нас одна свободная переменная это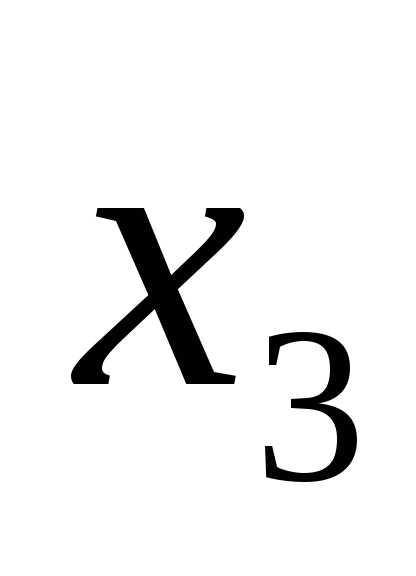 .
.
Выразим базисные переменные через свободные: 

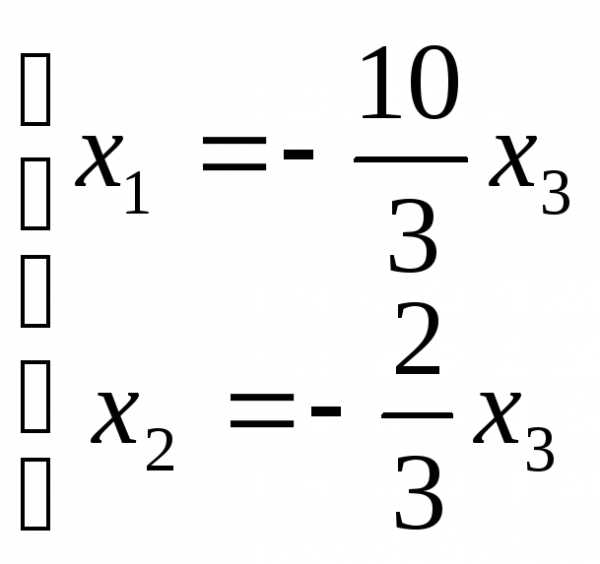 . Обозначая свободную переменную:
. Обозначая свободную переменную: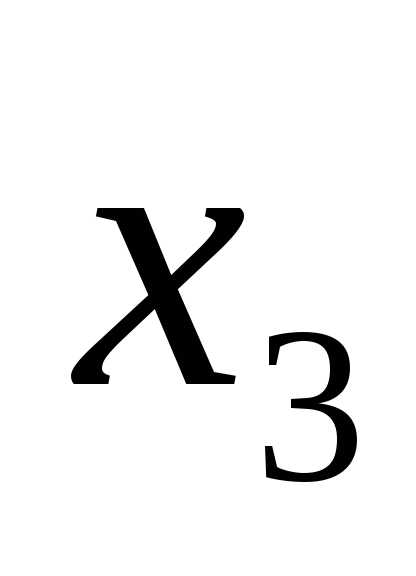 =
= , получаем общее решение в виде:
, получаем общее решение в виде: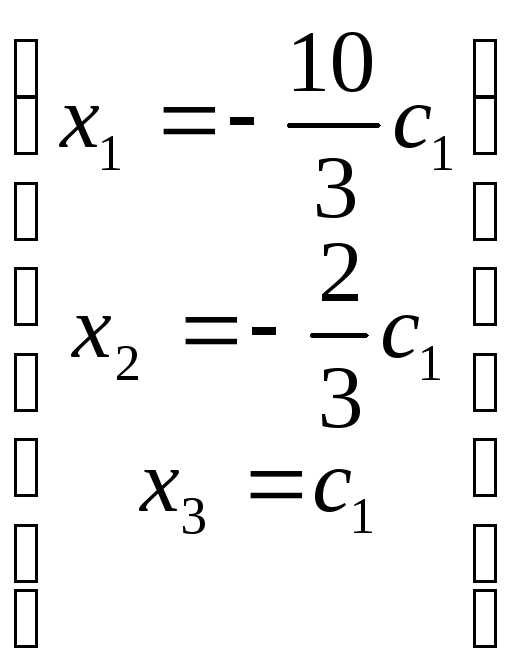
Пример 4.4
Найти общее решение системы: 
Решение.
Приведем расширенную матрицу системы к ступенчатому виду:
АВ= 


r(A)=r(AВ)=2<n, гдеn-число неизвестных, то система совместная и неопределенная. Запишем эквивалентную систему уравнений:
Примем за базисные переменные 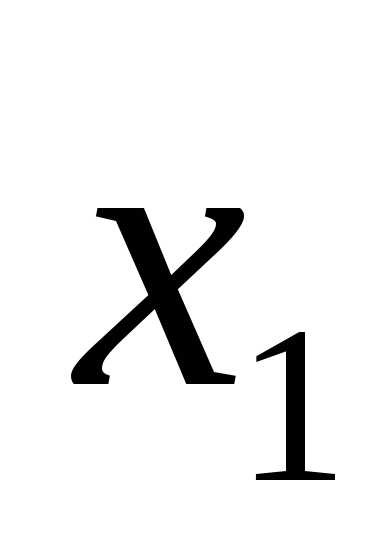 и
и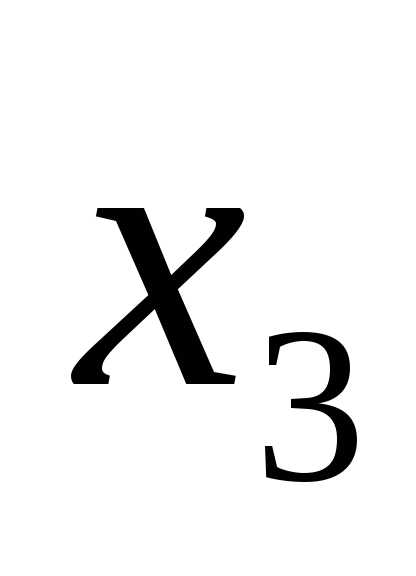 , а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (5-2)=3, значит
, а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (5-2)=3, значит ,
,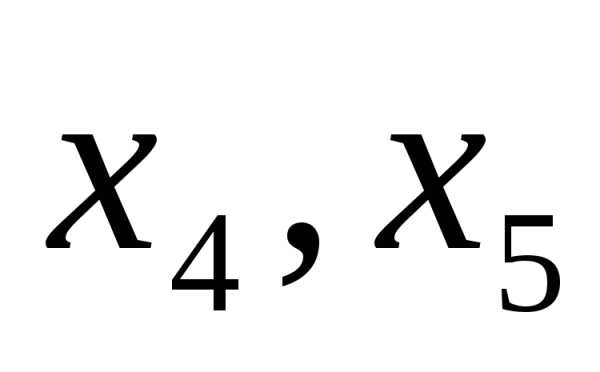 -свободные переменные.
-свободные переменные.
Выразим базисные переменные через свободные: 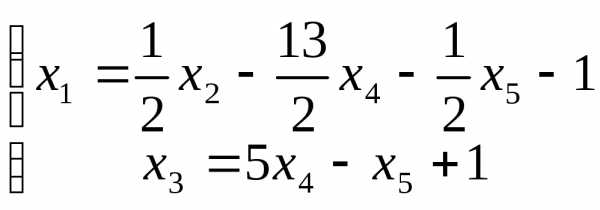 Обозначая свободную переменную:
Обозначая свободную переменную: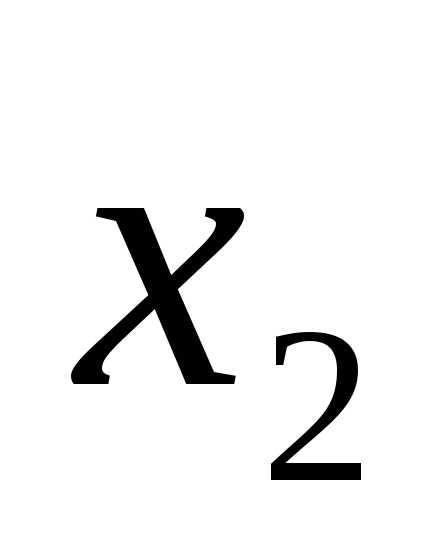 =
=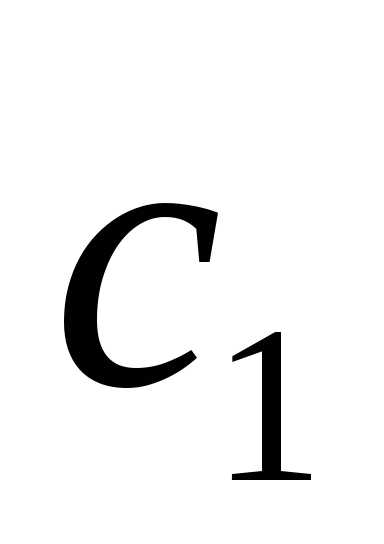 ,
,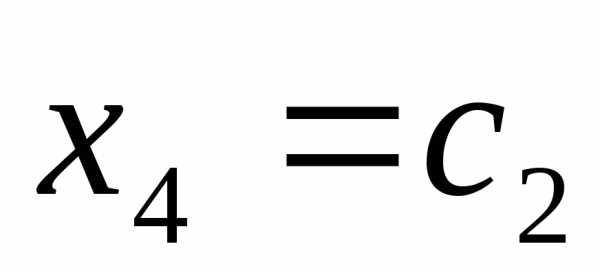 ,
, получаем общее решение в виде:
получаем общее решение в виде: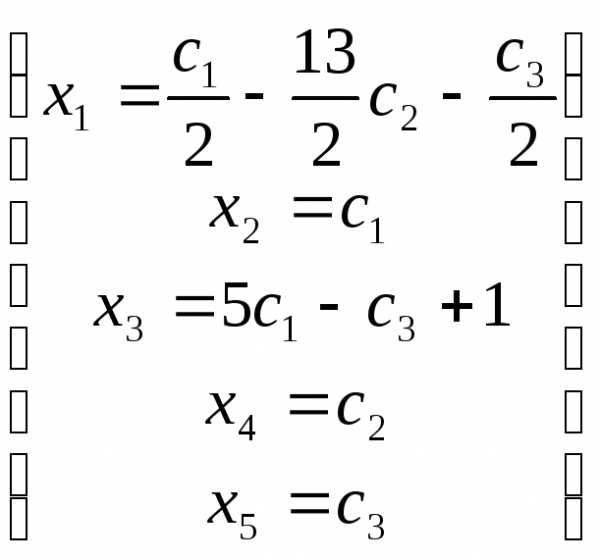 .
.
studfiles.net
Обратная матрица. Примеры вычисления
Нахождение обратной матрицы является важной составляющей в разделе линейной алгебры. С помощью таких матриц, если они существуют, можно быстро найти решение системы линейных уравнений.
Матрицаназывается обратной к матрице,если выполняются следующие равенства.
.
Если определитель матрицыотличен от нуля, то матрицу называют не особо или невырожденной.
Для того, чтобы матрица имела обратную необходимо и достаточно, чтобы она была невырожденной
Алгоритм нахождения обратной матрицы
Пусть имеем квадратную матрицу
и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:
1. Найти определитель матрицы. Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной
2. Найти алгебраические дополнения элементов матрицы . Они равны минорам, умноженным на в степени суммы строки и столбца, для которого ищем.
3. Составить матрицу из алгебраических дополнений элементов матрицы матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается .
4. Разделить присоединенную матрицу на детерминант . Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.
--------------------------------------------
Пример 1.
Найти матрицу, обратную к матрице (Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")
1) (1.127)
2) (1.130)
3) (1.133)
Решение.
1)Находим определитель матрицы
Так как детерминант не равен нулю (), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений
Матрица дополнений примет вид
Транспонируем ее и получаем присоединенную
Разделим ее на определитель и получим обратную
Видим, что в случае, когда определитель равен единице присоединена и обратная матрицы совпадают.
2) Вычисляем определитель матрицы
Находим матрицу алгебраических дополнений
Конечный вид матрицы дополнений
Транспонируем ее и находим союзную матрицу
Находим обратную матрицу
3) Вычислим детерминант матрицы. Для этого разложим его на первую строчку. В результате получим два отличны от нуля слагаемые
Находим матрицу алгебраических дополнений. Расписание определителя проводим по строкам и столбцам, в которых больше нулевых элементов (обозначены черным цветом).
Конечный вид матрицы дополнений следующий
Транспонируем ее и находим присоединенную матрицу
Поскольку определитель матрицы равен единице то обратная матрица совпадает с присоединенной. Данный пример назад.
При вычислениях обратной матрицы типичными являются ошибки связанные с неправильными знаками при вычислении определителя и матрицы дополнений.
--------------------------------------------
------------------------------
yukhym.com
Нахождение обратной матрицы: три алгоритма и примеры
Нахождение обратной матрицы - задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
,
произведение на которую матрицы А справа является единичной матрицей, т.е, . (1)
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
,
произведение на которую матрицы А справа является единичной матрицей, т.е, . (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и b равно единице: ab = 1. Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Для неособенной квадратной матрицы А обратной является матрица
, (2)
где - определитель матрицы А, а - матрица, союзная с матрицей А.
Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
Пример 1. Для матрицы
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу , транспонированную относительно матрицы A:
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
Следовательно, матрица , союзная с матрицей A, имеет вид
Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
.
В результате должна получиться обратная матрица.
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование - это система линейных уравнений, вид которой будет приведён ниже в алгоритме.
Алгоритм нахождения обратной матрицы методом линейных преобразований
1. Для данной невырожденной матрицы A составить линейное преобразование - систему линейных уравнений вида
,
где aij - элементы матрицы A.
2. Решить полученную систему относительно y - найти для предыдущего линейного преобразование обратное линейное преобразование
,
в котором Aij - алгебраические дополнения элементов матрицы A, Δ - определитель матрицы A. Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки - в столбце, а для элементов столбца - в строке.
3. Находим коэффициенты при y: , которые и будут элементами матрицы, обратной для матрицы A.
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований - это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.
Пример 4. Найти обратную матрицу для матрицы
.
Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:
.
Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:
Коэффициенты при иксах в обратном линейном преобразовании - это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:
Начало темы "Матрицы"
Другие темы линейной алгебры
function-x.ru
Метод присоединенной матрицы
Количество просмотров публикации Метод присоединенной матрицы - 502
Определение обратной матрицы
ОБРАТНЫЕ МАТРИЦЫ
ЛЕКЦИЯ 3
Обратная матрица Метод присоединенной матрицы. Матричные уравнения. Матричный способ решения систем линейных уравнений. Ранг матрицы. Метод окаймляющих миноров. Метод элементарных преобразований. Теорема о базисном миноре.
Матрица А–1 принято называть обратной матрицей по отношению к матрице А, в случае если выполняется равенство
AA–1 = A–1A = E. (3.1)
Из данного определения следует, что взаимообратные матрицы перестановочны. Это означает, что только квадратные матрицы могут иметь обратные. При этом не каждая квадратная матрица имеет обратную. Для того чтобы матрица А имела обратную, крайне важно и достаточно, чтобы ее определитель был отличен от нуля: detA¹0.
% Действительно, из определения обратной матрицы и свойств определителей получаем: det(A–1A)=detA–1detA=detE=1, откуда следует крайне важно е условие существования обратной матрицы: detA¹0 или detA–1¹0. Вопрос о доказательстве достаточности этого условия несколько сложнее. Для этого нужно указать алгоритм построения такой матрицы. По этой причине мы вернемся к этому вопросу позднее (см. метод присоединенной матрицы).
Отметим, что если обратная матрица существует, то такая матрица только одна. Действительно, пусть существует еще одна матрица В, удовлетворяющая условию АВ=ВА=Е, тогда можно написать:
BAA–1=(BA)A–1=EA–1=A–1,
BAA–1=B(AA–1)=BE=B,
откуда получаем В=А–1, ᴛ.ᴇ. обратные матрицы совпадают. &
Матрица, определитель которой отличен от нуля, принято называть невырожденной, или неособенной; в противном случае она принято называть вырожденной, или особенной. Необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: обратная матрица существует, причем только одна, тогда и только тогда, когда исходная матрица невырожденная.
Стоит сказать, что для невырожденных матриц справедливы следующие свойства:
| 1) detA–1=(detA)–1, | 2) (AB)–1=B–1A–1, | 3) (AT)–1=(A–1)T, |
| 4) (A–1)–1=A, | 5) (An)–1=(A–1)n. |
Матрица AÚпринято называть присоединенной к матрице A, если она является транспонированной к матрице A, а вместо элементоввзяты их алгебраические дополнения, ᴛ.ᴇ.
Теорема 3.1. Обратная и присоединенная матрицы связаны соотношением
(3.2)
% Действительно, рассмотрим произведение матриц
При этом учтем, что сумма произведений элементов некоторой строки или столбца на их алгебраические дополнения равно определителю матрицы (см. теорему о разложении определителя по строке или столбцу).Дополнительно мы воспользуемся еще одним свойством определителей: сумма произведений алгебраических дополнений некоторой строки или столбца на соответствующие элементы другой строки или столбца равно нулю. Это связано с тем, что такая сумма эквивалентна определителю, у которого две одинаковые строки или столбца, и, следовательно, он будет равен нулю. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, перемножая рассматриваемые матрицы, получим
Отсюда следует справедливость приведенной теоремы. Более того, фактически мы указали алгоритм построения обратной матрицы при помощи присоединенной матрицы и тем самым доказали достаточное условие существования обратной матрицы. &
Общая схема нахождения обратной матрицы (метод присоединенной матрицы):
1) Вычисляем определитель заданной матрицы, в случае если он равен нулю, то обратной матрицы не существует.
2) Транспонируем заданную матрицу.
3) Вычисляем все алгебраические дополнения транспонированной матрицы.
4) Составляем присоединенную матрицу, ᴛ.ᴇ. вместо элементов транспонированной матрицы ставим их алгебраические дополнения.
5) Записываем обратную матрицу. Для этого каждый элемент присоединенной матрицы делим на определитель исходной матрицы.
6) Делаем проверку.
Пример 3.1. Найти A–1, если
Решение. 1) detA = –4.
2)
3) Ищем алгебраические дополнения транспонированной матрицы (не забывать учитывать знаки алгебраических дополнений!):
4) Составляем присоединенную матрицу:
5) Записываем обратную матрицу:
6) Делаем проверку: AA–1 = A–1A = E:
Следовательно, обратная матрица найдена правильно. à
Пример 3.2. Найти обратную матрицу
Решение. Поскольку
и A11 = d, A12 = –c, A21 = –b, A22 = a, то
Эту формулу можно использовать для нахождения обратных матриц второго порядка. à
referatwork.ru
Обратная матрица и методы ее вычисления
Запишем вспомогательную матрицу
и приведем её, с помощью элементарных преобразований, к матрице, в которой единичная матрица будет слева. Переставим местами первую и вторую строки
Прибавим ко второй строке первую строку, умноженную на а к третьей строке первую, умноженную на
Прибавим ко второй строке третью, умноженную на
Умножим вторую строку на
Прибавим к первой строке вторую, умноженную на а к третьей вторую, умноженную на
Разделим третью строку на 3
К первой строке прибавим третью, умноженную на
Тогда обратная матрица равна
ru.solverbook.com
Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если выполняется условие: АА-1= А-1А=Е, где Е - единичная матрица того же порядка, что и матрица А. Обратная А-1матрица имеет ту же размерность, что и матрица А.
Определение. Квадратная матрица А=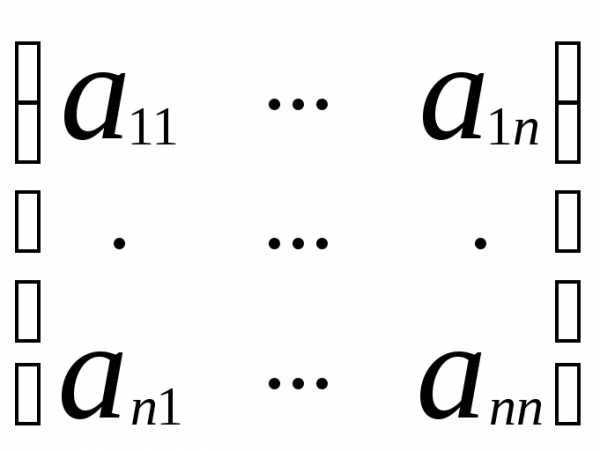 называется невырожденной, если её определитель неравен нулю, в противном случае матрица называется вырожденной.
называется невырожденной, если её определитель неравен нулю, в противном случае матрица называется вырожденной.
Теорема.Всякая невырожденная матрица имеет обратную.
Определение. Присоединенной матрицей к матрице А называется матрица вида:
к матрице А называется матрица вида:
 =
= , где Аij-алгебраическое дополнение элемента аij.
, где Аij-алгебраическое дополнение элемента аij.
Находят обратную матрицу поформуле: А-1=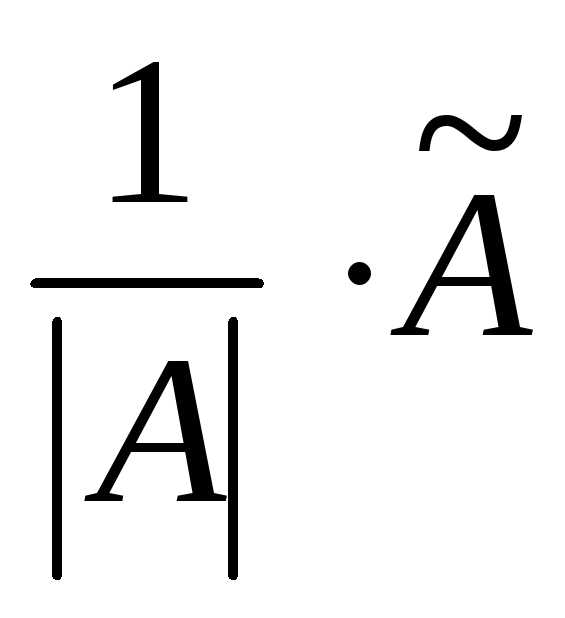 .
.
Пример 3.1
Найти обратную матрицу методом присоединенной матрицы.
А=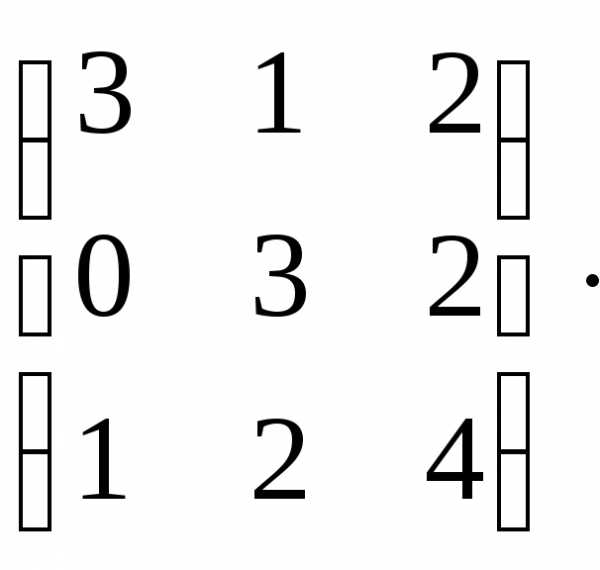
Решение.
Выясним, является ли данная матрица невырожденной. Для этого найдем определитель матрицы:
 =3(-1)1+1
=3(-1)1+1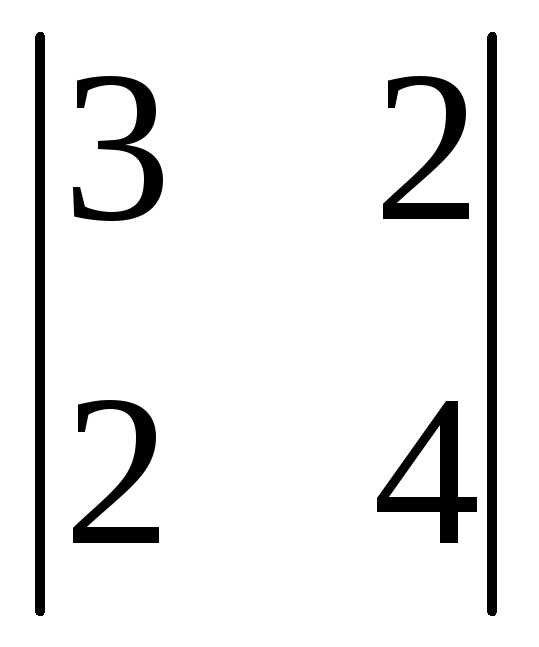 +0(-1)2+1
+0(-1)2+1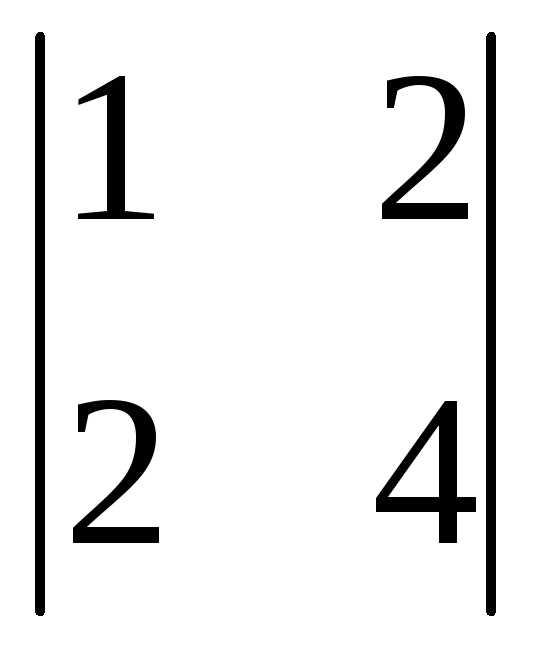 +1(-1)3+1=3(12-4)+0+(2-6)=24-4=20.
+1(-1)3+1=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0, следовательно, данная матрица имеет обратную.
0, следовательно, данная матрица имеет обратную.
Найдем транспонированную матрицу.
АТ=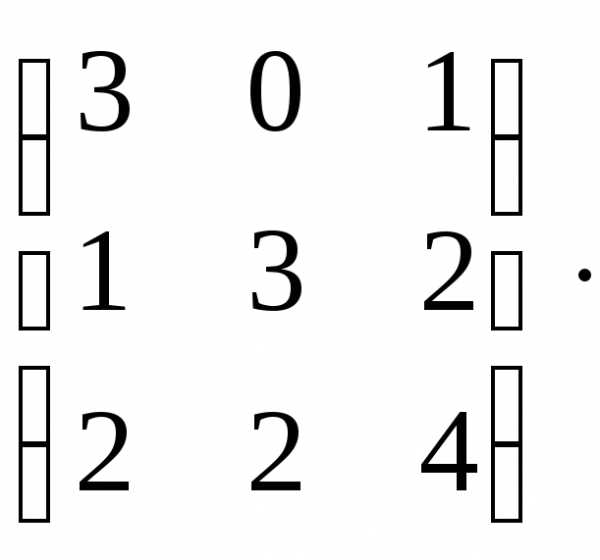
Вычислим присоединенную матрицу. Для этого найдем алгебраическое дополнение каждого элемента матрицы.
 = (-1)1+1
= (-1)1+1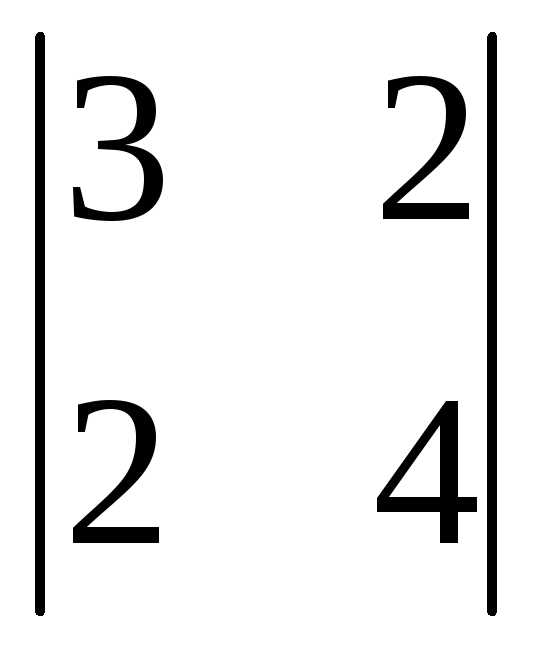 =12-4=8
=12-4=8
 = (-1)1+2
= (-1)1+2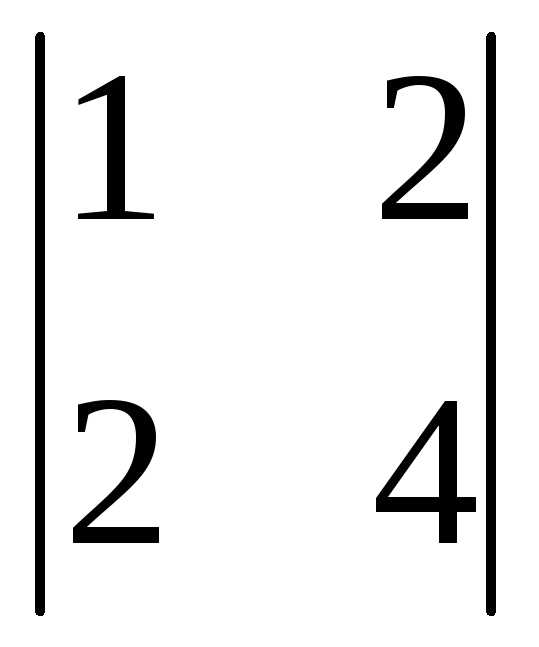 = -(4-4)= 0
= -(4-4)= 0
 = (-1)1+3
= (-1)1+3 = 2-6= -4
= 2-6= -4
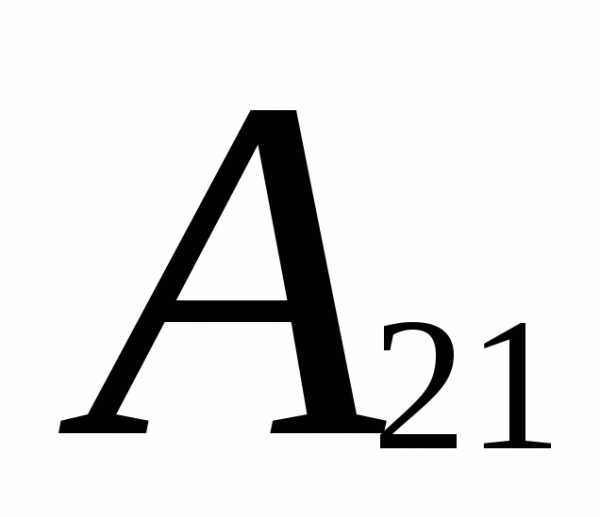 = (-1)2+1
= (-1)2+1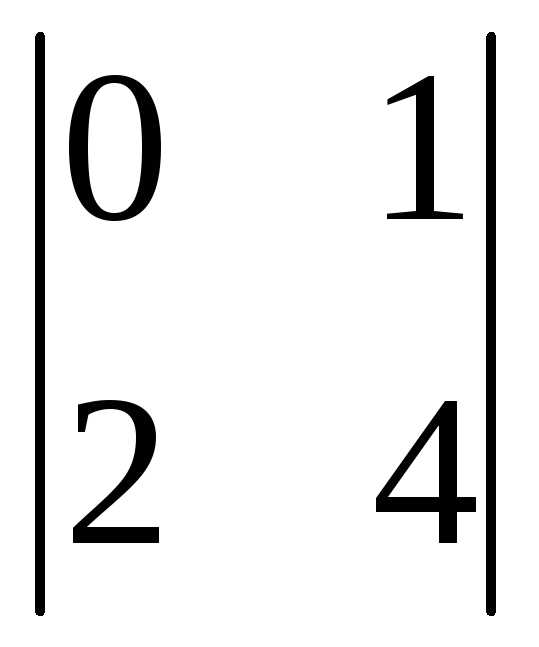 = -(0-2)=2
= -(0-2)=2
 = (-1)2+2
= (-1)2+2 = 12-2=10
= 12-2=10
 = (-1)2+3
= (-1)2+3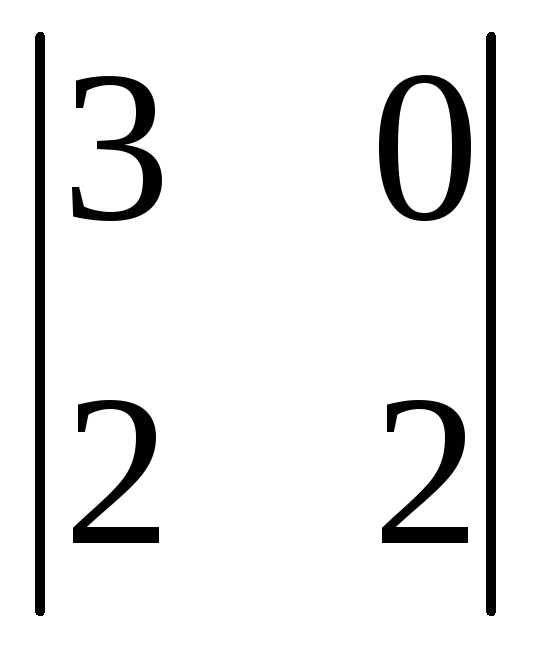 = -(6-0)= -6
= -(6-0)= -6
 = (-1)3+1
= (-1)3+1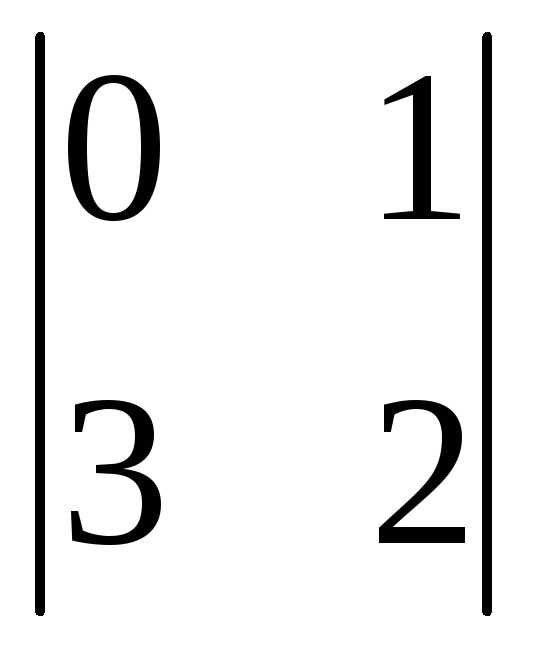 = 0-3= -3
= 0-3= -3
 = (-1)3+2
= (-1)3+2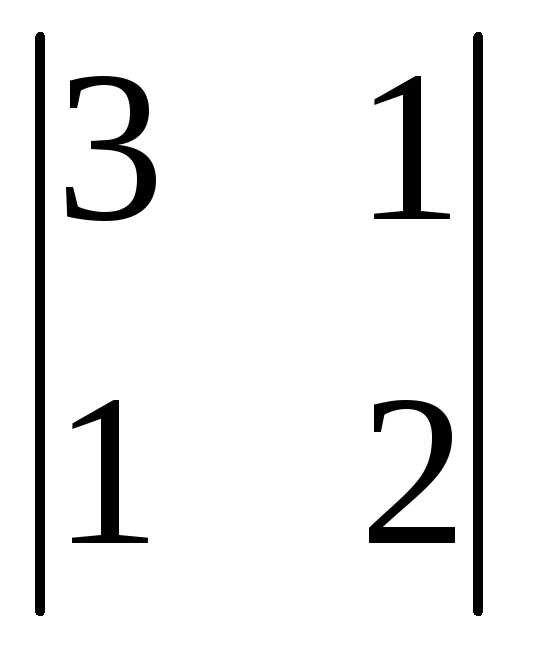 = -(6-1)= -5
= -(6-1)= -5
 = (-1)3+3
= (-1)3+3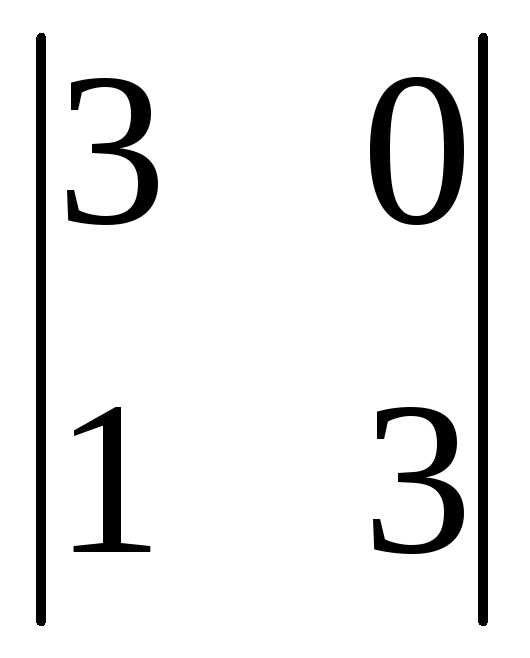 = 9-0=9.
= 9-0=9.
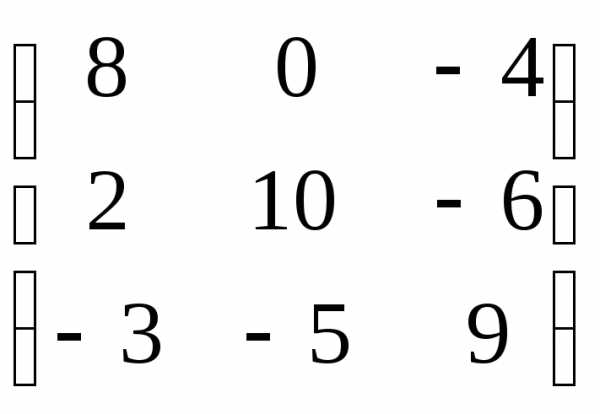
 =
=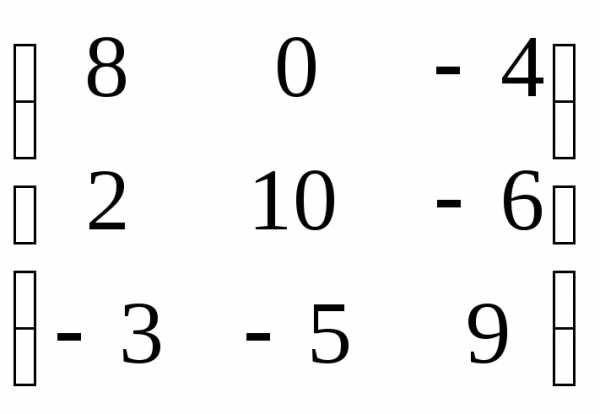
4. Воспользуемся формулой: А-1=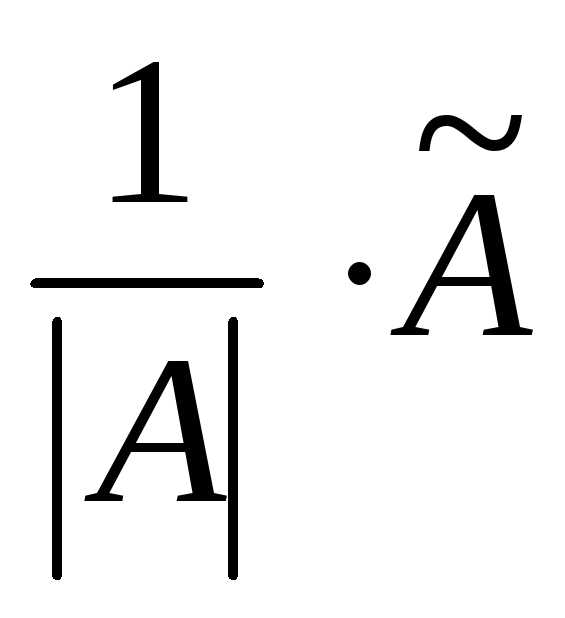 .
.
А-1=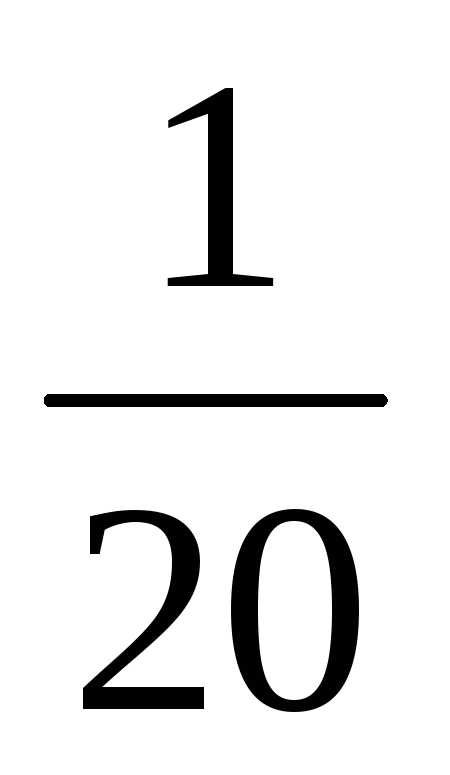
 =
=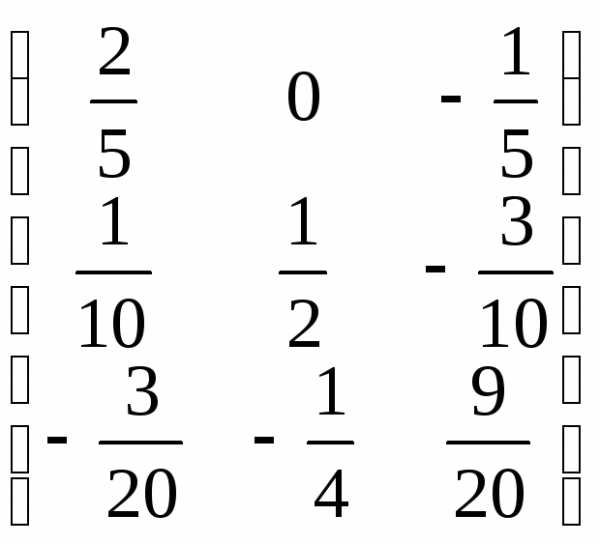 .
.
Решение систем линейных уравнений методом обратной матрицы
Пусть дана система линейных уравнений . Обозначим её через (1). Выпишим основную матрицу данной системы: А=
. Обозначим её через (1). Выпишим основную матрицу данной системы: А= , вектор-столбец неизвестных:X=
, вектор-столбец неизвестных:X=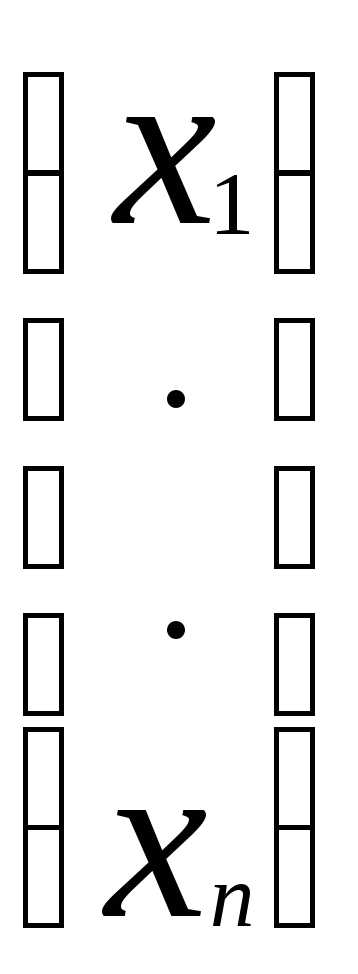 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B= . Теперь перепишем систему (1) в матричной форме:AX=B
. Теперь перепишем систему (1) в матричной форме:AX=B X=A-1B- решение системы (1).
X=A-1B- решение системы (1).
Пример 3.2
Решить систему линейных уравнений: 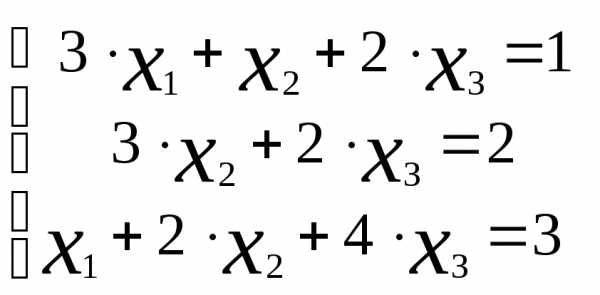 методом обратной матрицы.
методом обратной матрицы.
Решение.
Формула, по которой будем находить решение системы: X=A-1B.
Основная матрица системы А=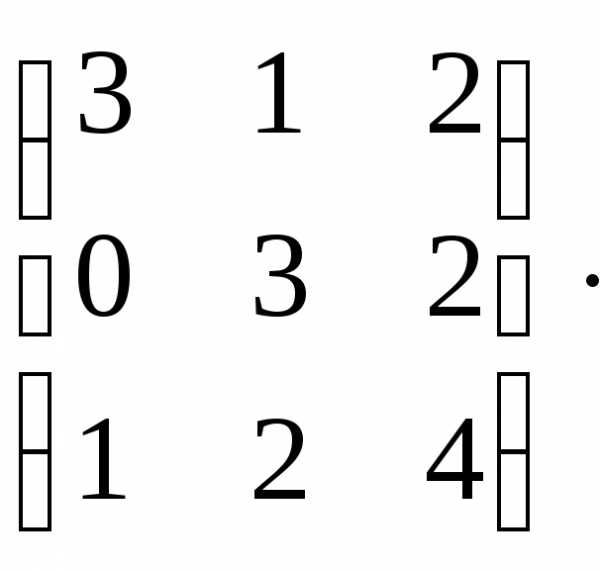 , вектор-столбец неизвестных:X=
, вектор-столбец неизвестных:X=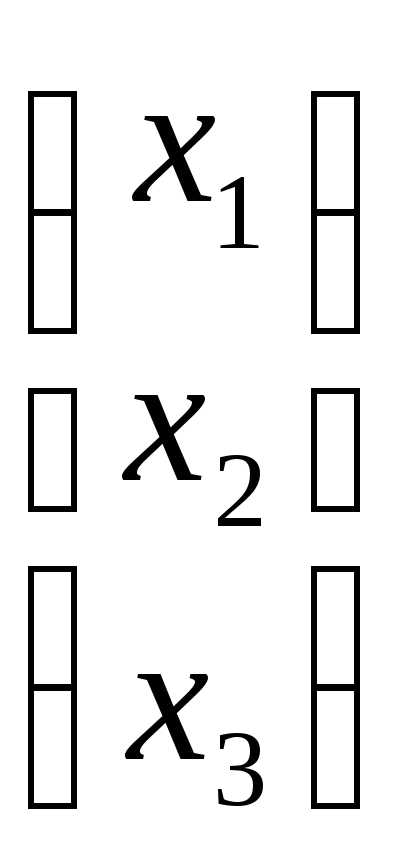
 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=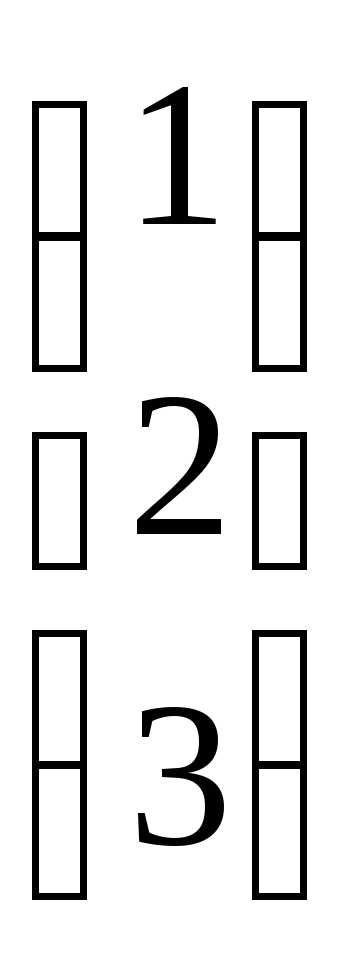 .
.
Найдем определитель  =3(-1)1+1
=3(-1)1+1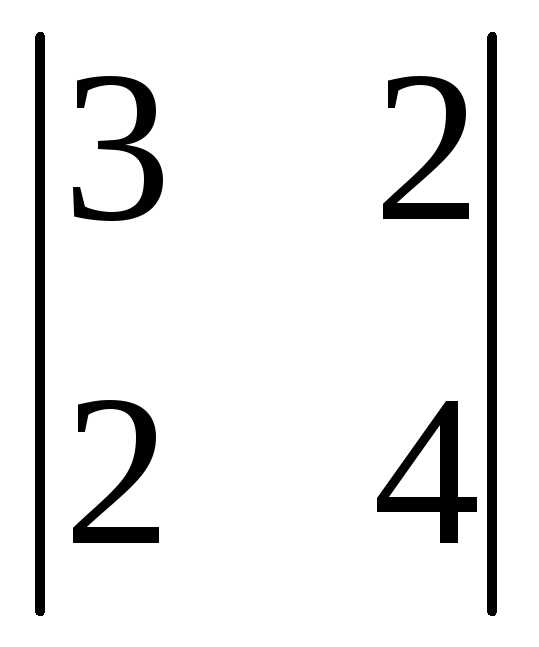 +0(-1)2+1
+0(-1)2+1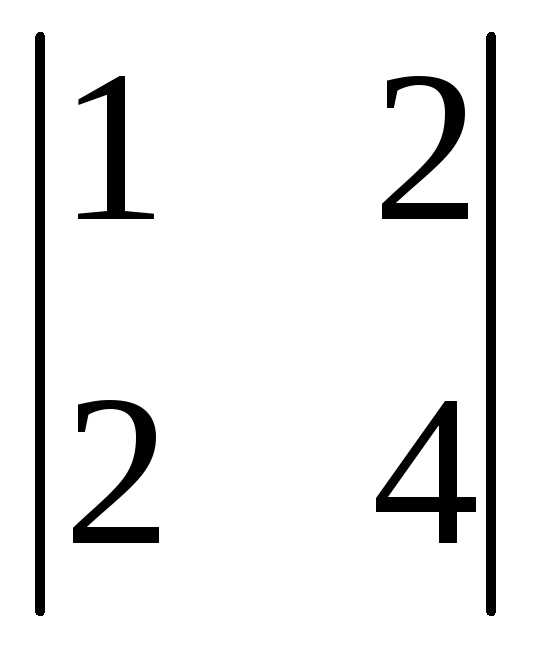 +1(-1)3+1
+1(-1)3+1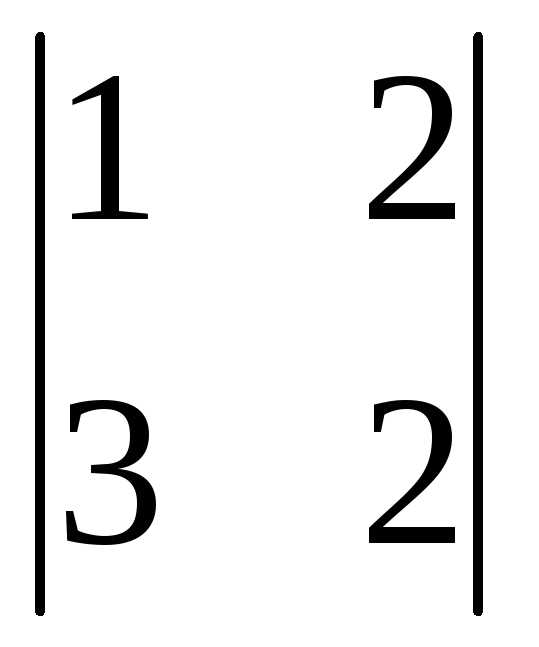 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0, следовательно, данная матрица имеет обратную.
0, следовательно, данная матрица имеет обратную.
Найдем обратную матрицу с помощью присоединенной матрицы (см. пример 3.1):
А-1=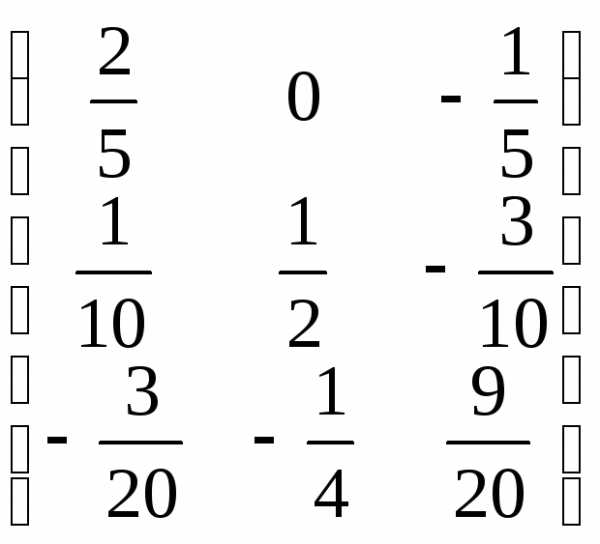 .
.
Подставим в формулу X=A-1B, получим:X=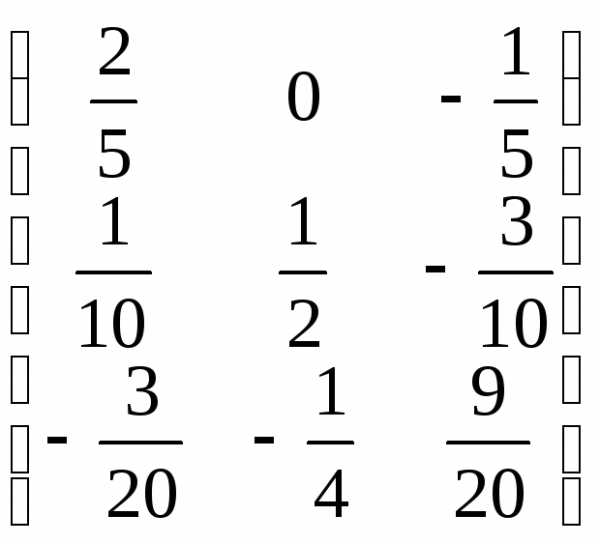
 =
= =
=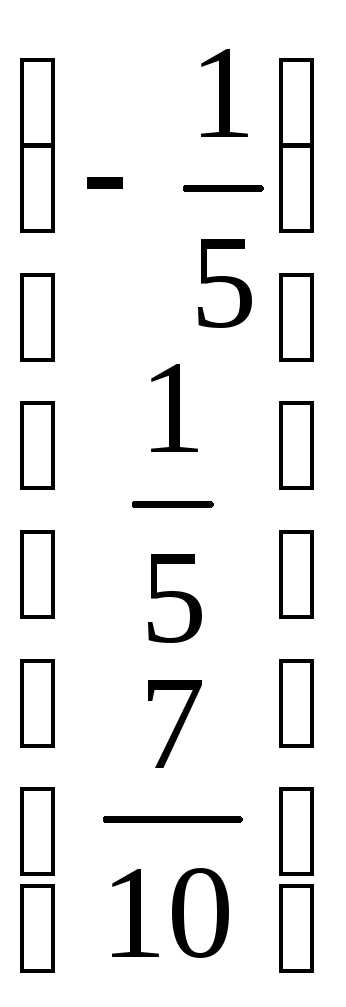
Ответ: 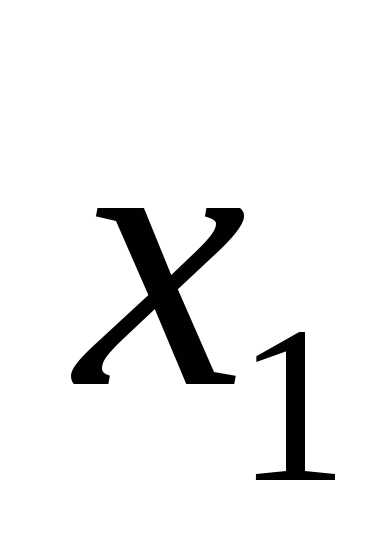 =
=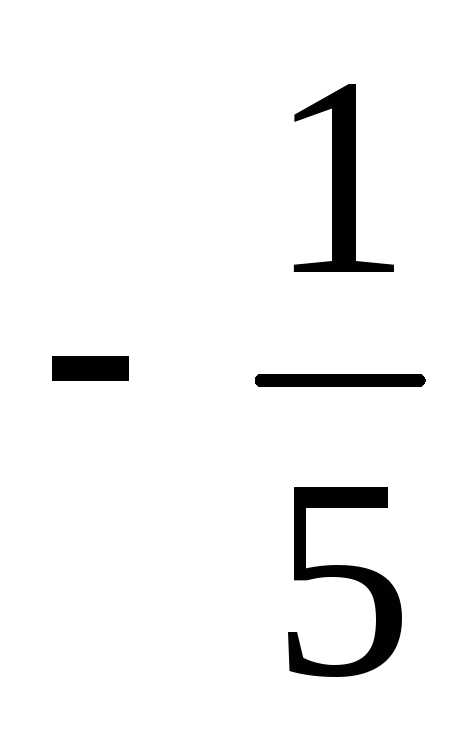 ,
, 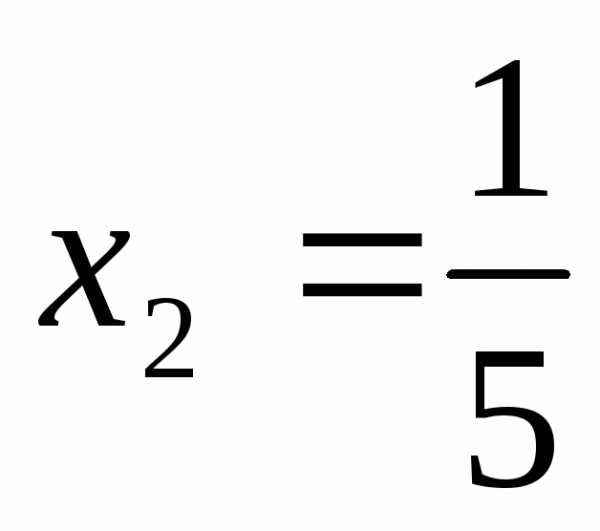 ,
,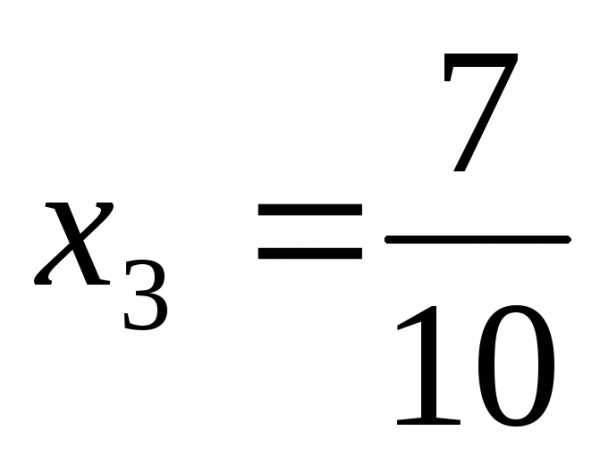 .
.
Правильность решения легко проверить, подставив полученные результаты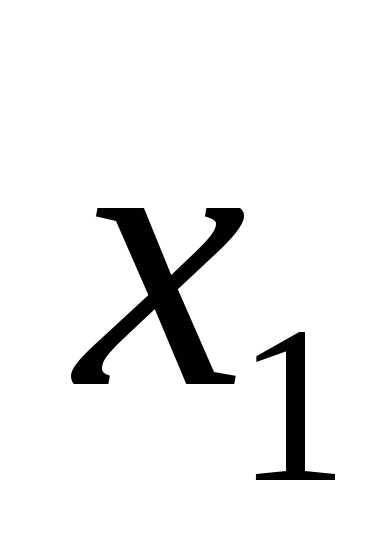 ,
, 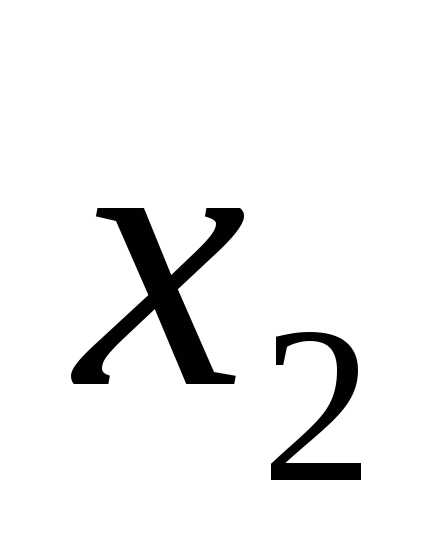 ,
, 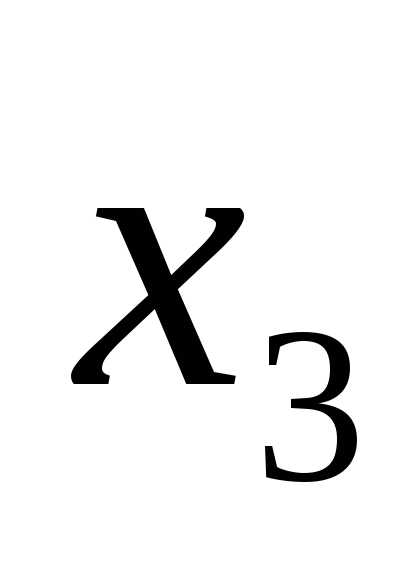 в данную систему уравнения.
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений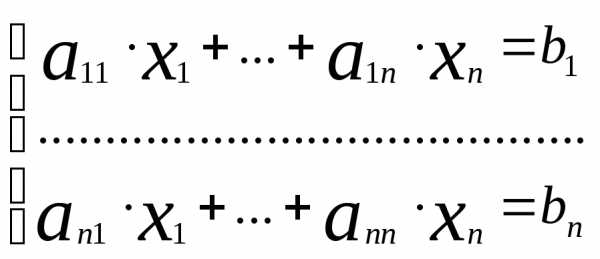 . Обозначим её через (1). Основная матрица данной системы: А=
. Обозначим её через (1). Основная матрица данной системы: А=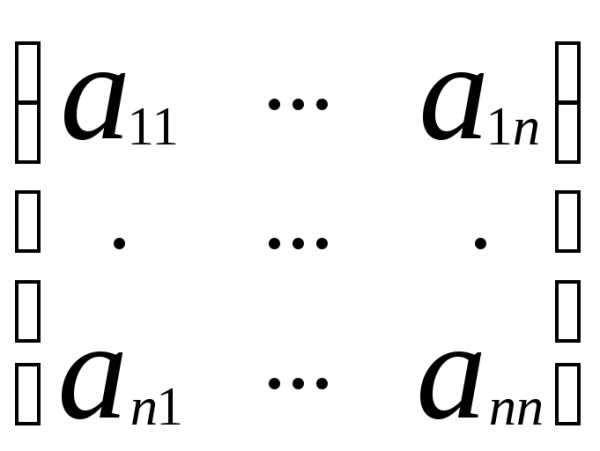 , вектор-столбец неизвестных:X=
, вектор-столбец неизвестных:X=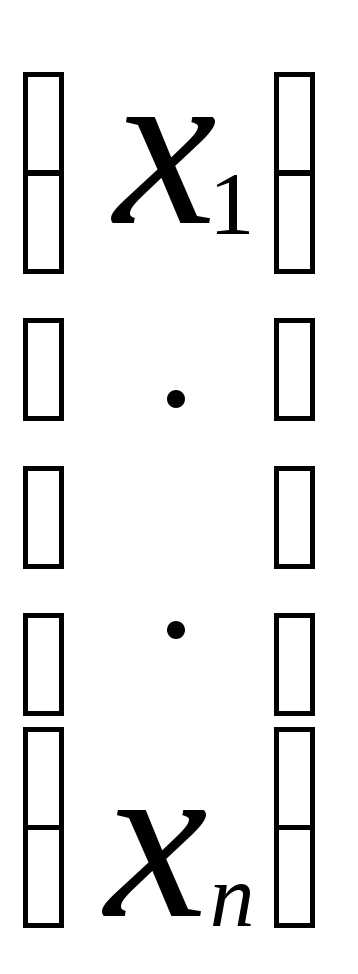 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=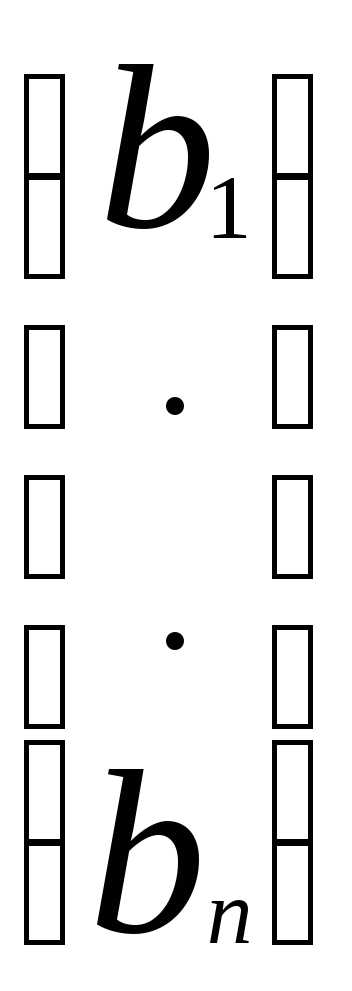 . Теперь запишем систему (1) в матричной форме:AX=B.
. Теперь запишем систему (1) в матричной форме:AX=B.
Теорема Крамера. Пусть  -определитель матрицы А,
-определитель матрицы А,  j-определитель матрицы, получаемой из А заменойj-го столбца столбцом свободных членов. Тогда, если
j-определитель матрицы, получаемой из А заменойj-го столбца столбцом свободных членов. Тогда, если
 0, то система имеет единственное решение:
0, то система имеет единственное решение: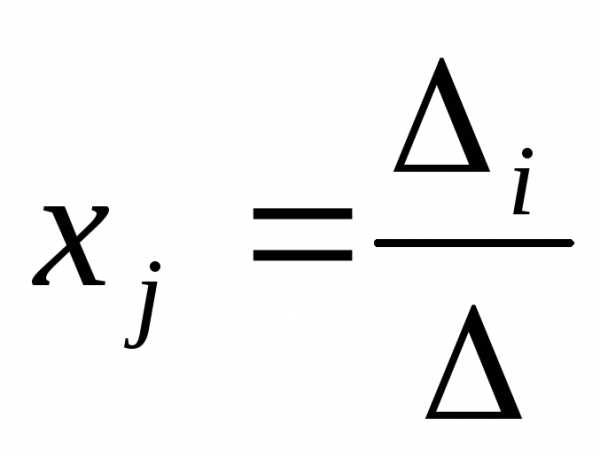 , (1jn).
, (1jn).
Пример 4.1
Решить систему линейных уравнений: 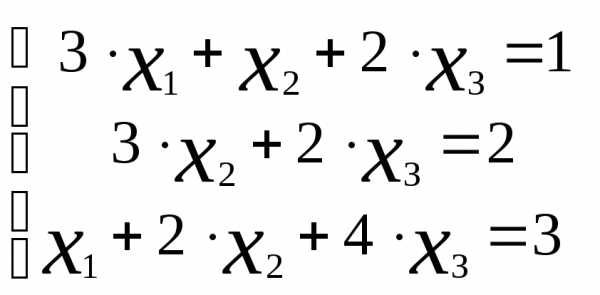 методом Крамера.
методом Крамера.
Решение.
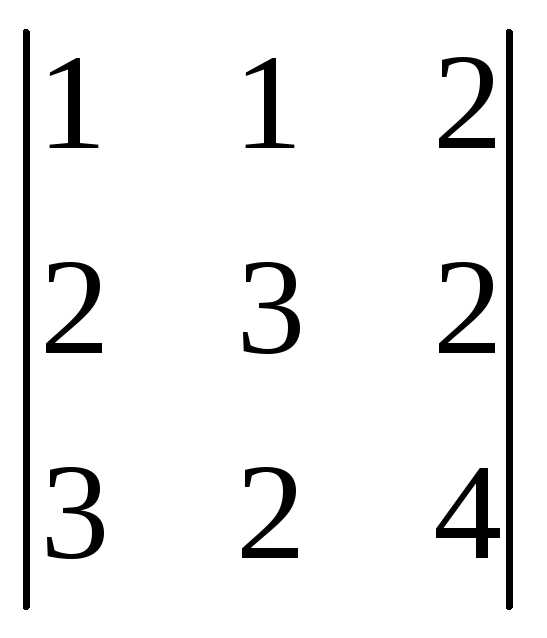
Основная матрица системы А=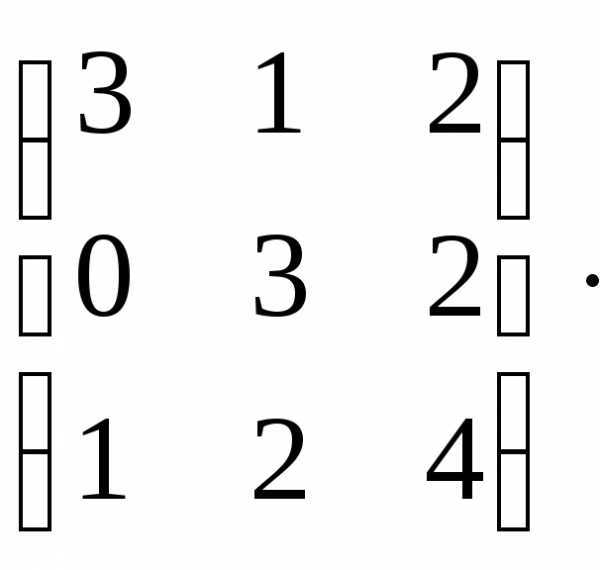 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=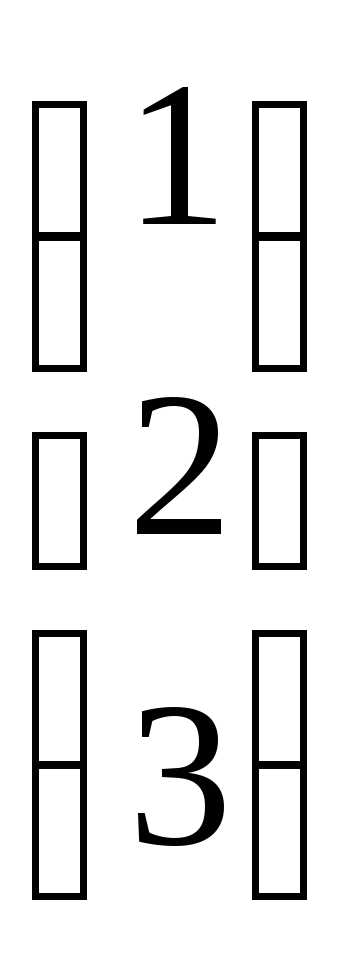 .
.
Найдем определитель  =
= =3(-1)1+1
=3(-1)1+1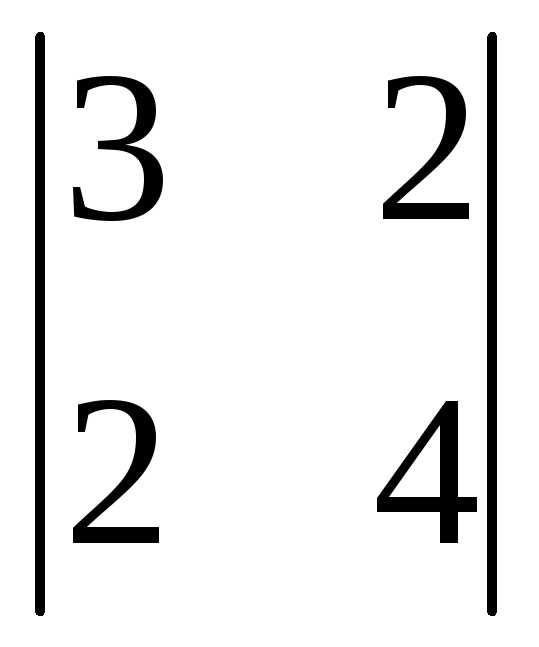 +0(-1)2+1
+0(-1)2+1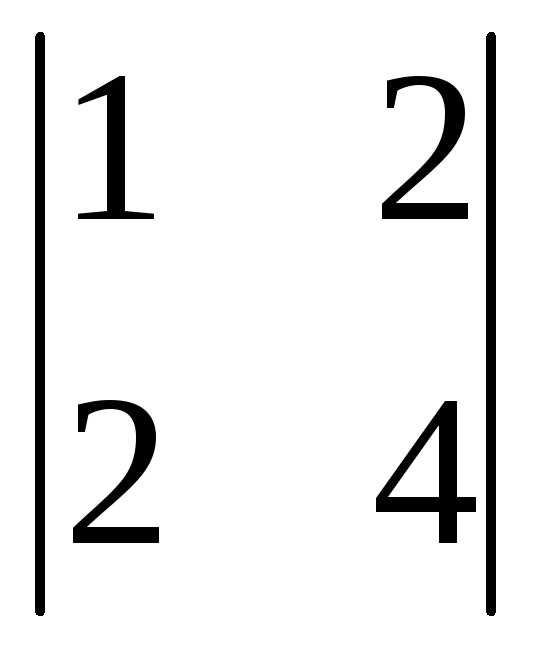 +1(-1)3+1
+1(-1)3+1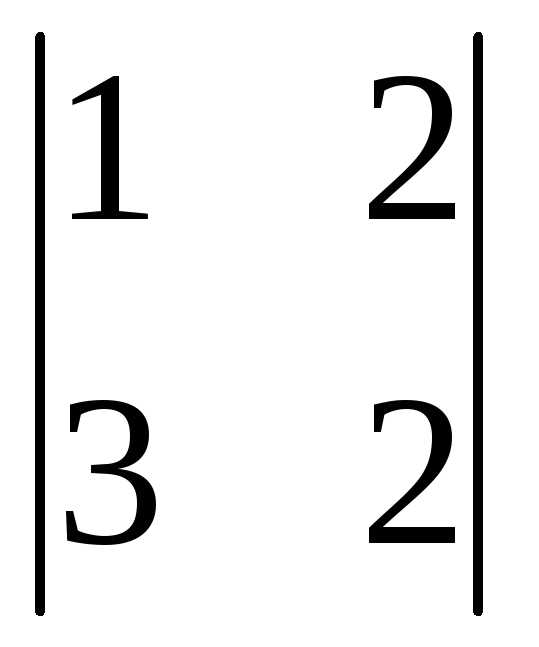 =3(12-4)+0+(2-6)=24-4=20. Т.к.
=3(12-4)+0+(2-6)=24-4=20. Т.к. 0, следовательно, можно применить формулы Крамера.
0, следовательно, можно применить формулы Крамера.
Найдем определители 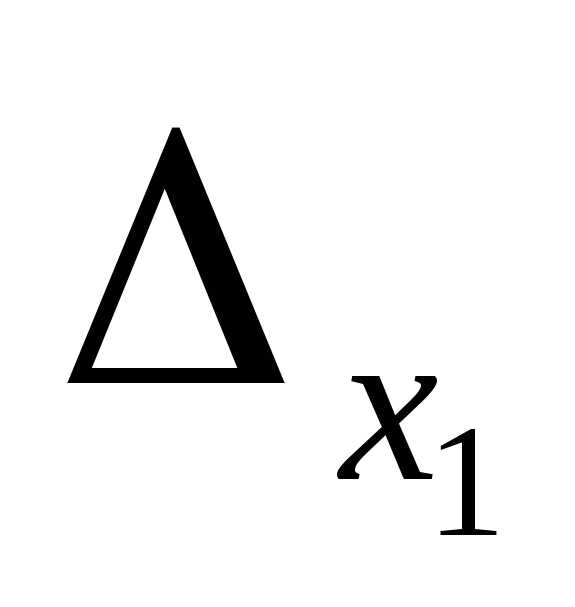 ,
,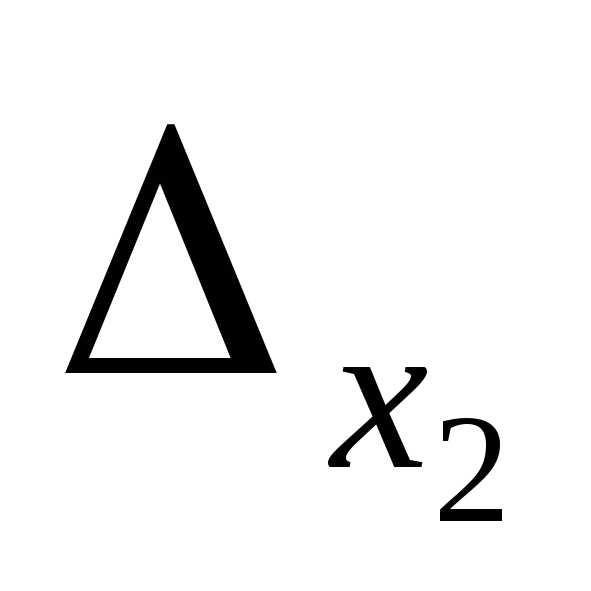 ,
,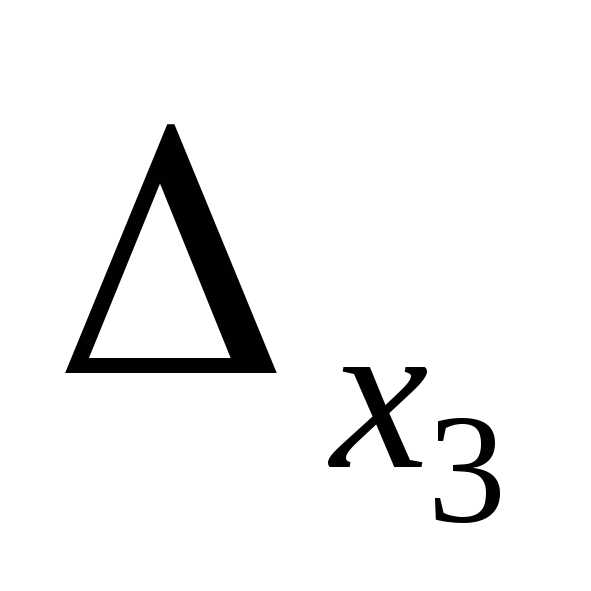 , полученные заменой соответствующих столбцов столбцом свободных членов:
, полученные заменой соответствующих столбцов столбцом свободных членов:
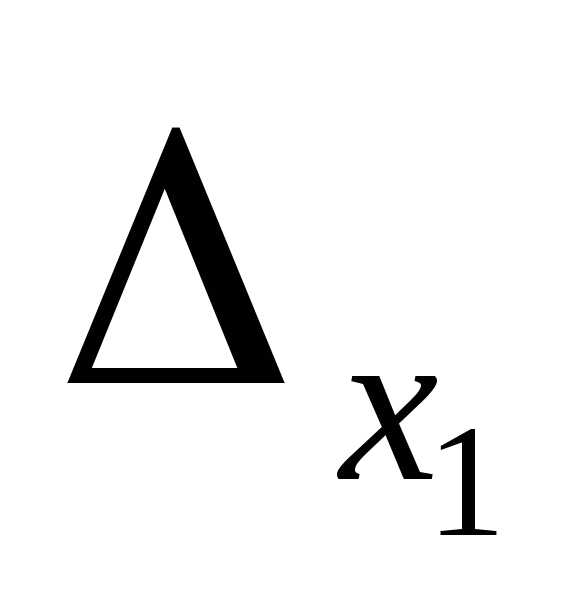 =
= =1(12-4)-1(8-6)+2(4-9)=8-2-10= -4;
=1(12-4)-1(8-6)+2(4-9)=8-2-10= -4;
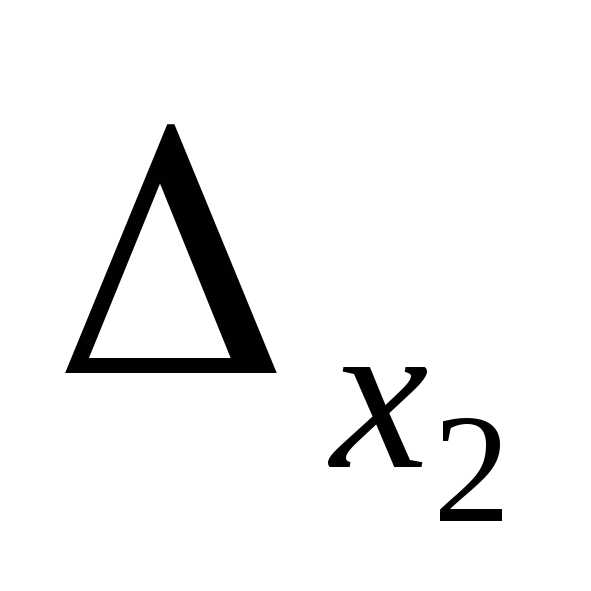 =
=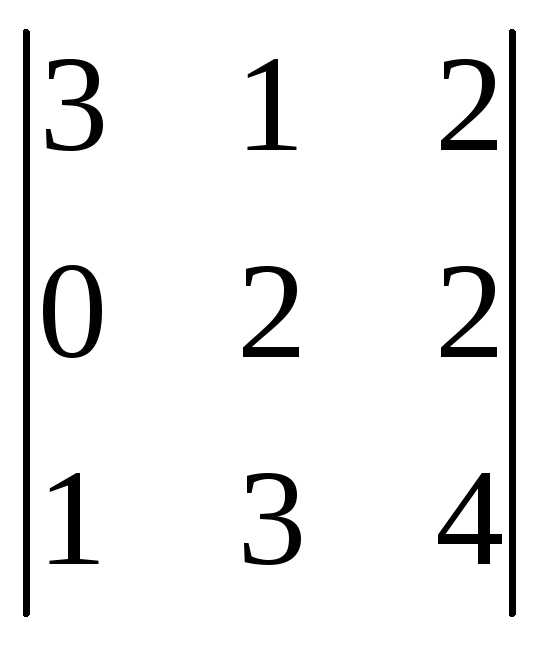 =3(8-6)-0+1(2-4)=6-2=4;
=3(8-6)-0+1(2-4)=6-2=4;
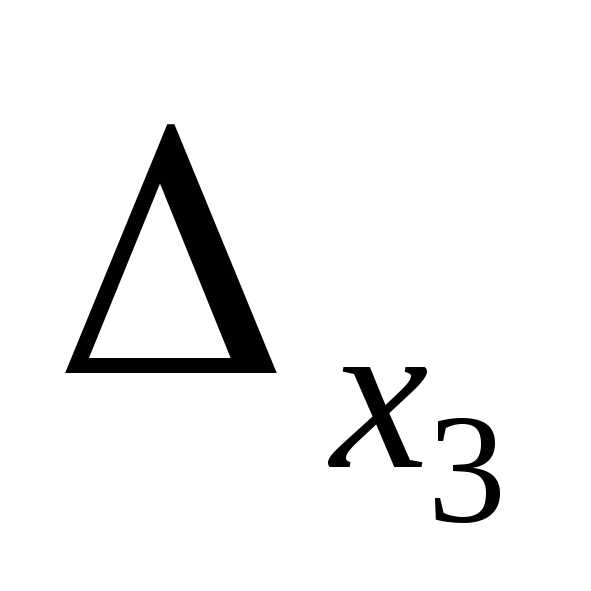 =
=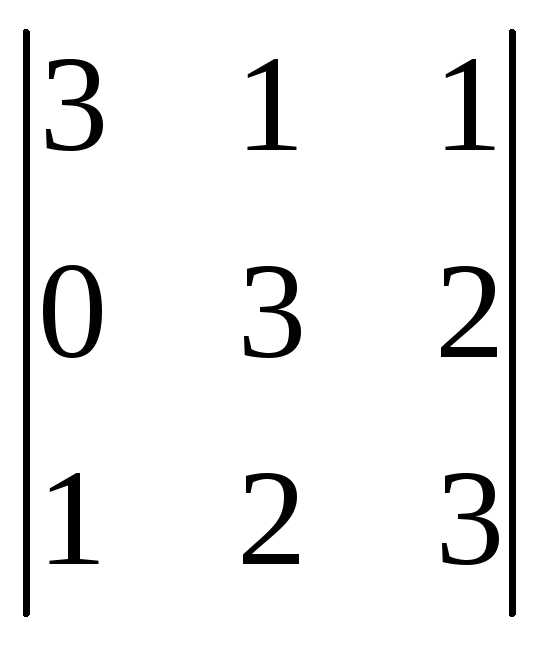 =3(9-4)-0+1(2-3)=15-1=14.
=3(9-4)-0+1(2-3)=15-1=14.
Тогда, по формуле Крамера:
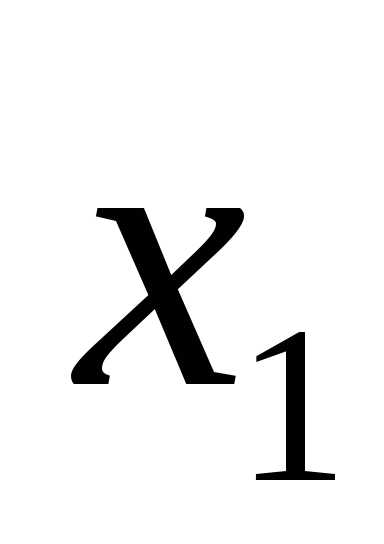 =
=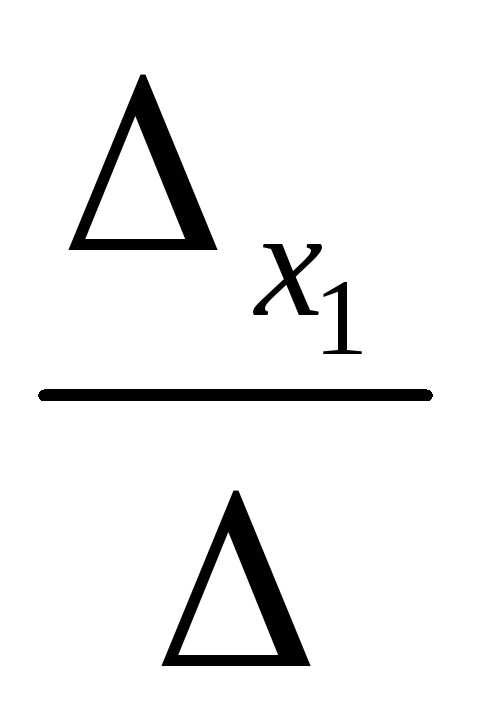 = -
= -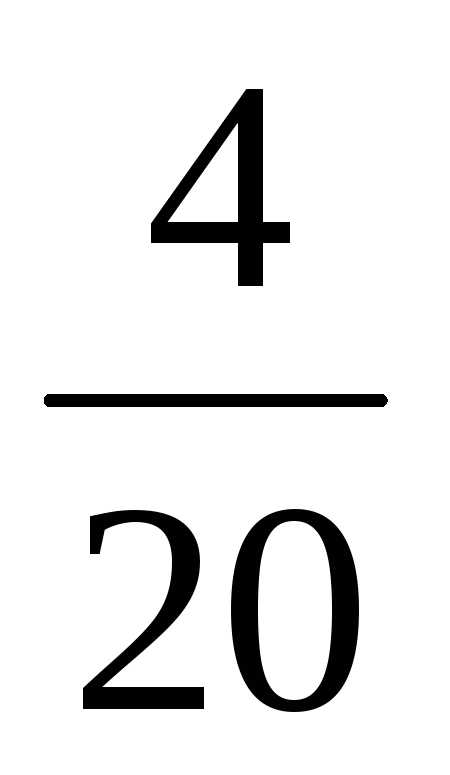 =
=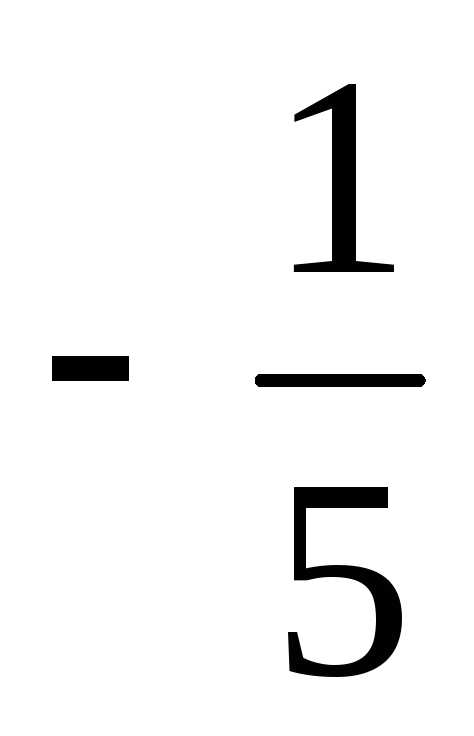 ;
;
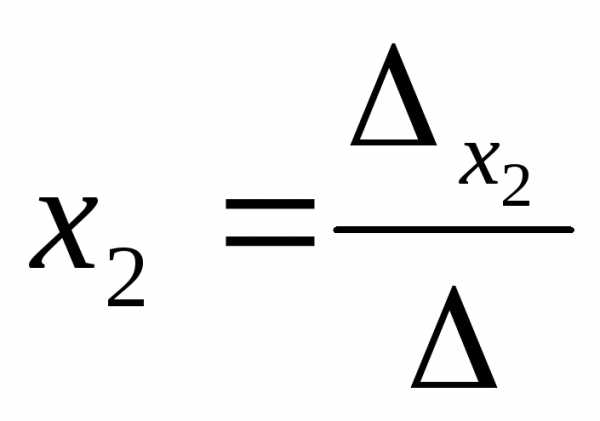 =
=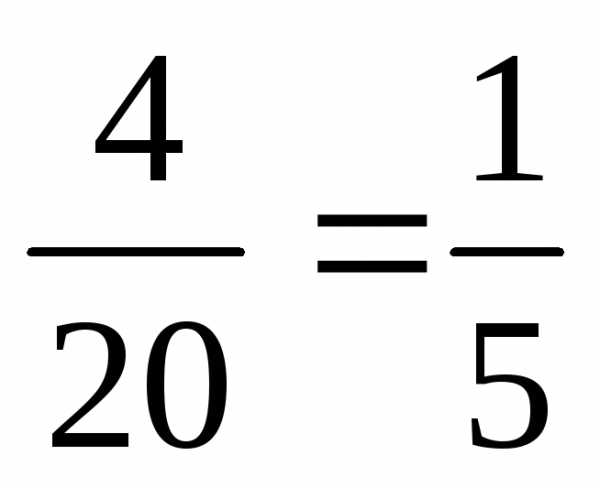 ;
;
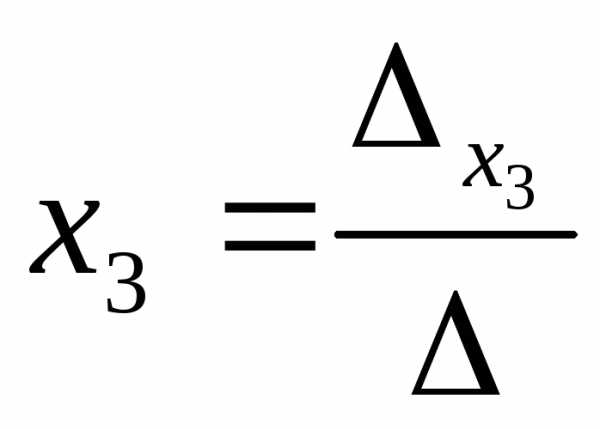 =
=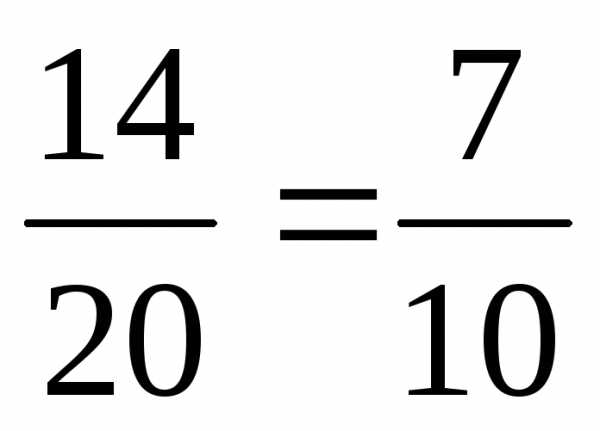 .
.
Ответ: 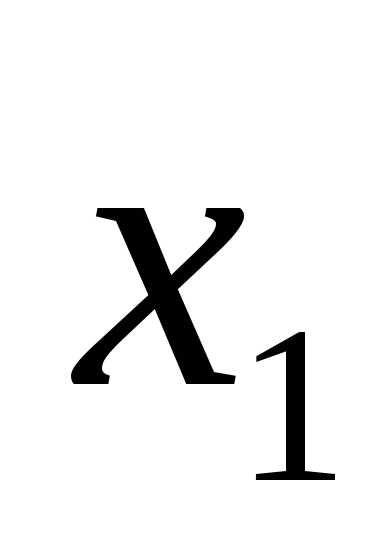 =
=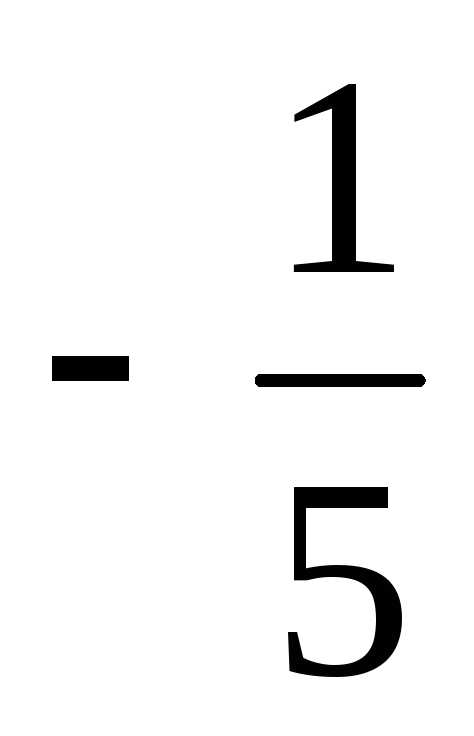 ,
, 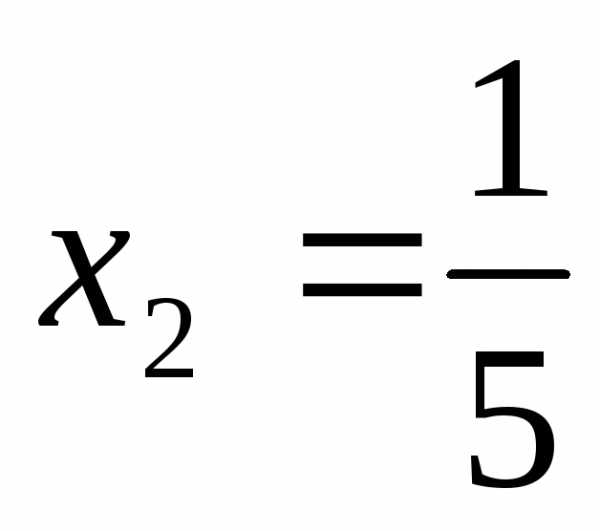 ,
,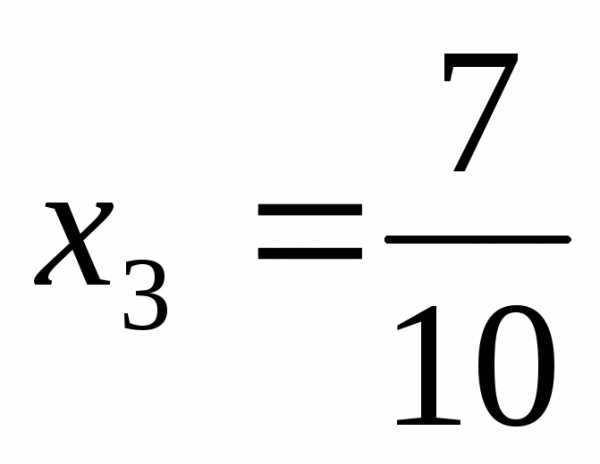 .
.
Решение систем линейных уравнений методом Гаусса
Пусть дана система линейных уравнений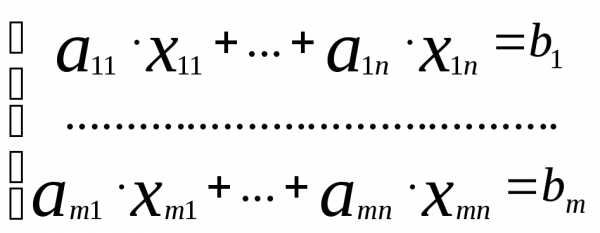 . Рассмотрим расширенную матрицу (АВ) данной системы и с помощью элементарных преобразований приведем её к ступенчатому виду, в результате получим расширенную матрицу (АВ).
. Рассмотрим расширенную матрицу (АВ) данной системы и с помощью элементарных преобразований приведем её к ступенчатому виду, в результате получим расширенную матрицу (АВ).
Если ранг основной матрицы системы меньше ранга расширенной матрицы r(A)<r(АВ), то система несовместна. Еслиr(A)=r(АВ)=n, гдеn-число неизвестных, то система совместна и определена. Еслиr(A)=r(АВ)<n, гдеn-число неизвестных, то система совместна и неопределенна.
Записываем систему линейных уравнений из полученной ступенчатой матрицы. Определяем базисные и свободные переменные, и выражая базисные переменные через свободные получаем решение системы.
Пример 4.2
Решить систему линейных уравнений: 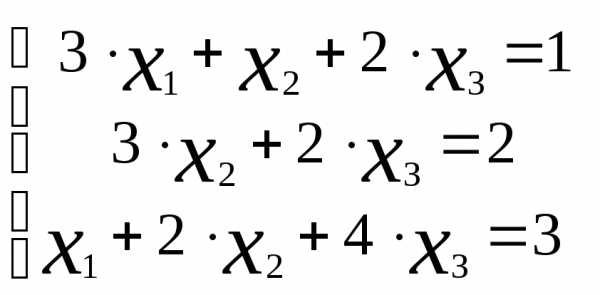 методом Гаусса.
методом Гаусса.
Решение.
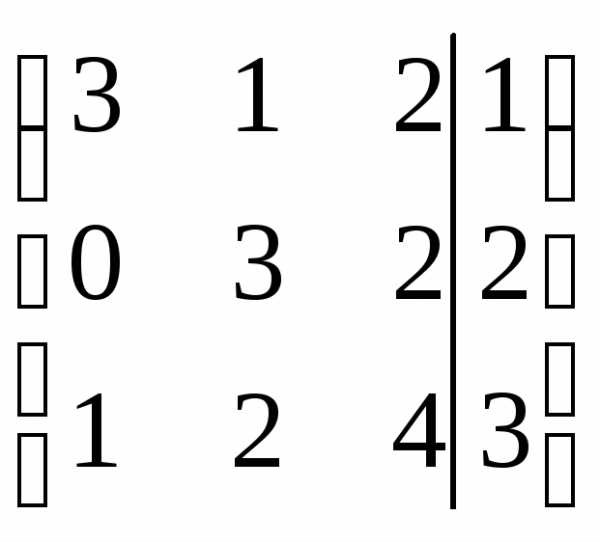

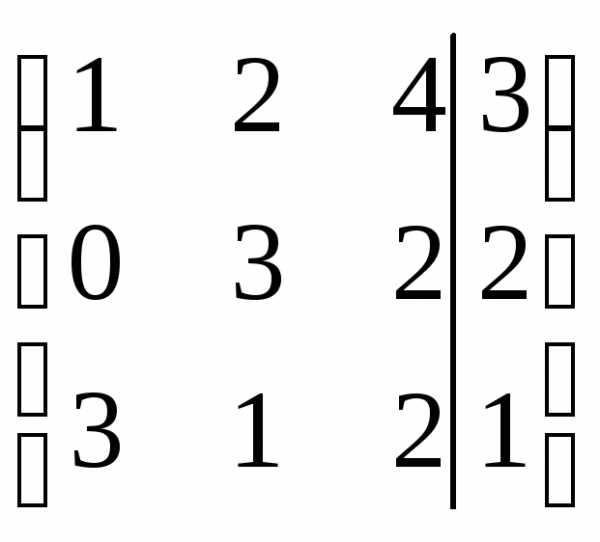
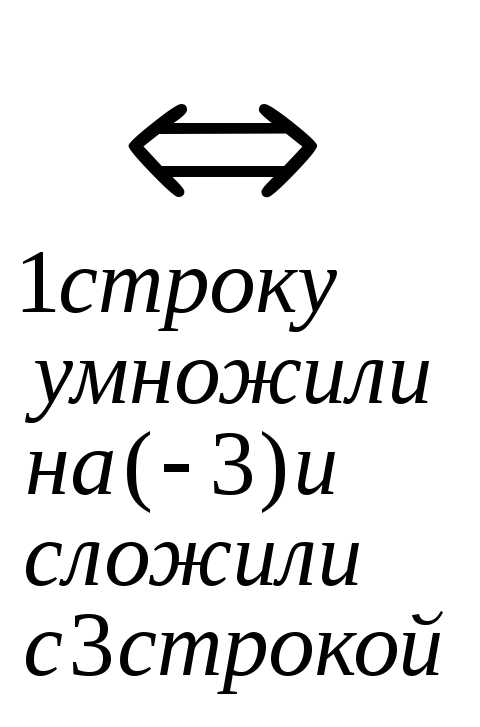
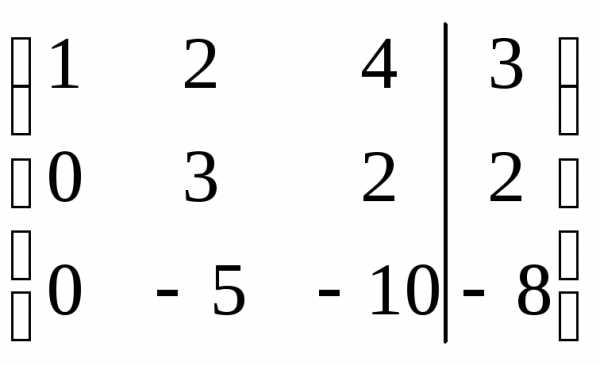
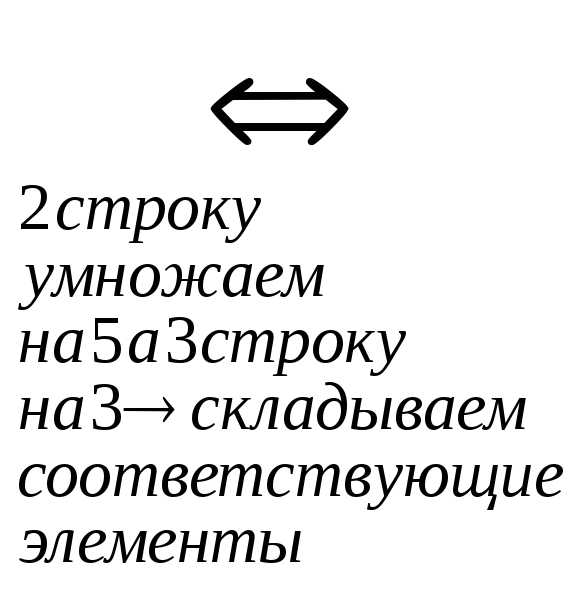
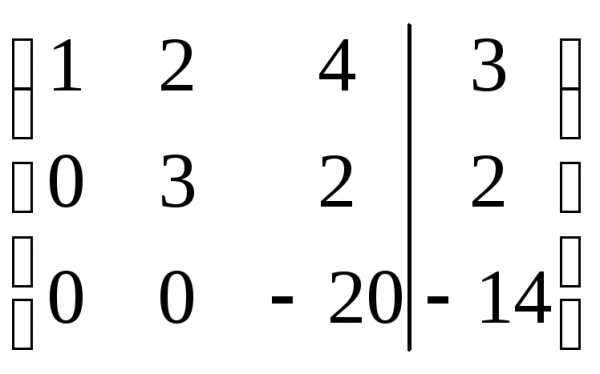
r(A)=r(АВ)=n система совместна и определена.
система совместна и определена.
Отсюда, запишем эквивалентную систему уравнений, имеем: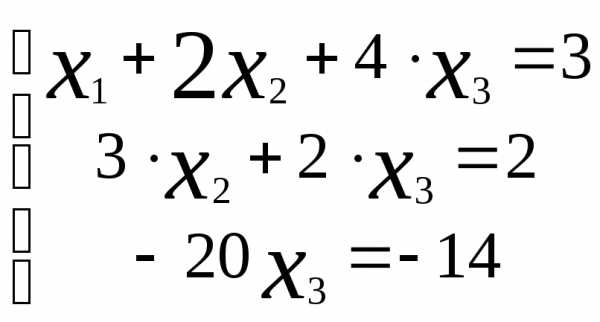
Решая её, получаем: 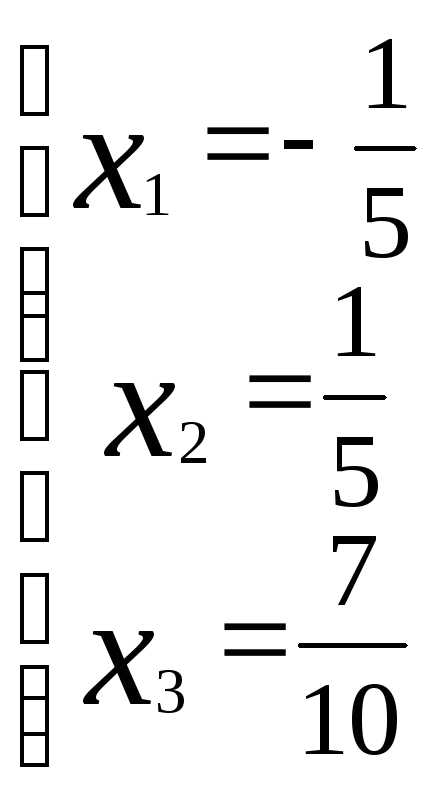
Ответ: 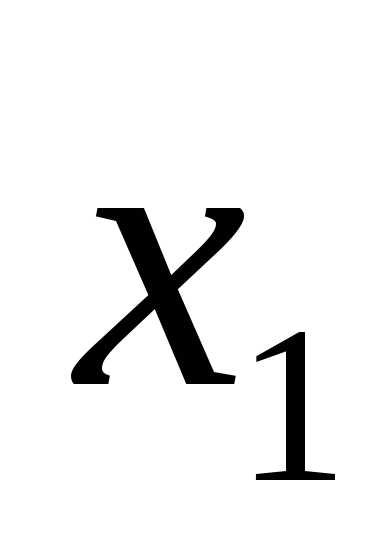 =
=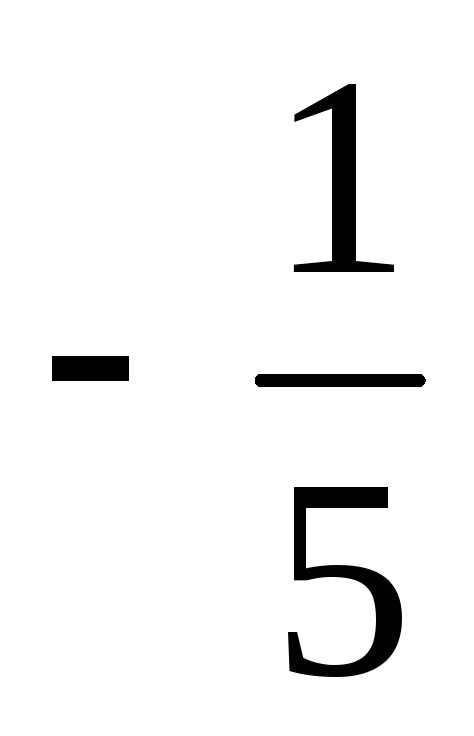 ,
, 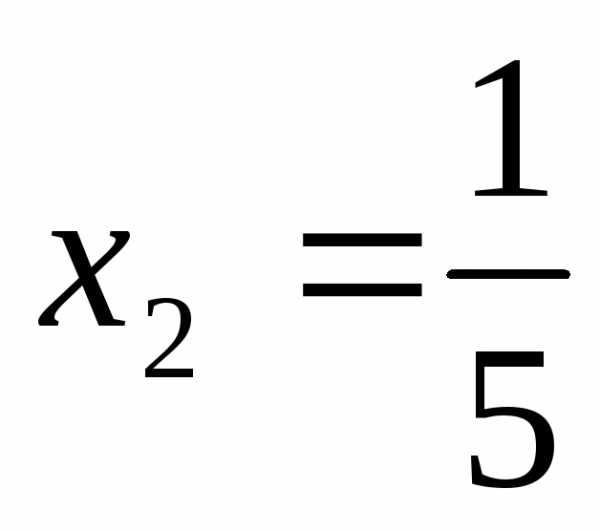 ,
,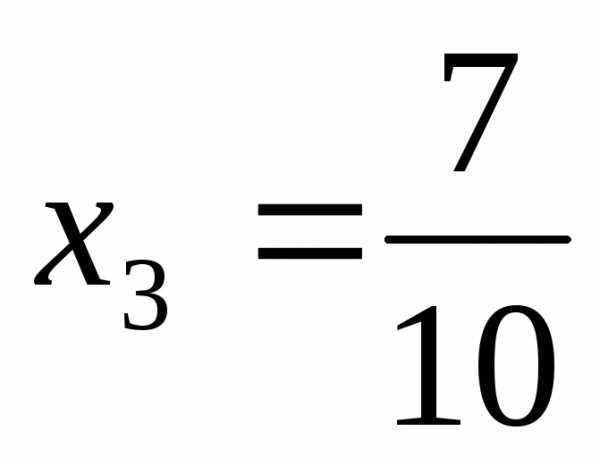 .
.
Пример 4.3
Найти общее решение системы: 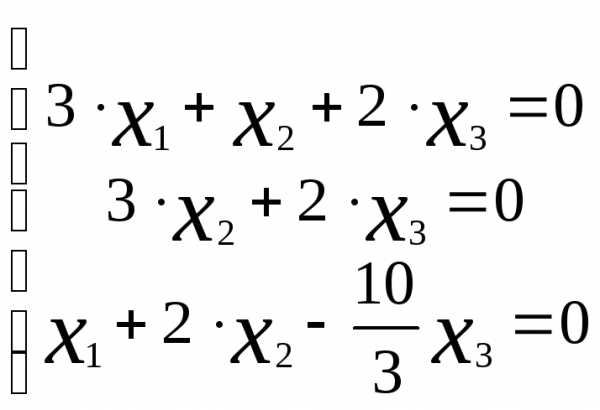 .
.
Решение.
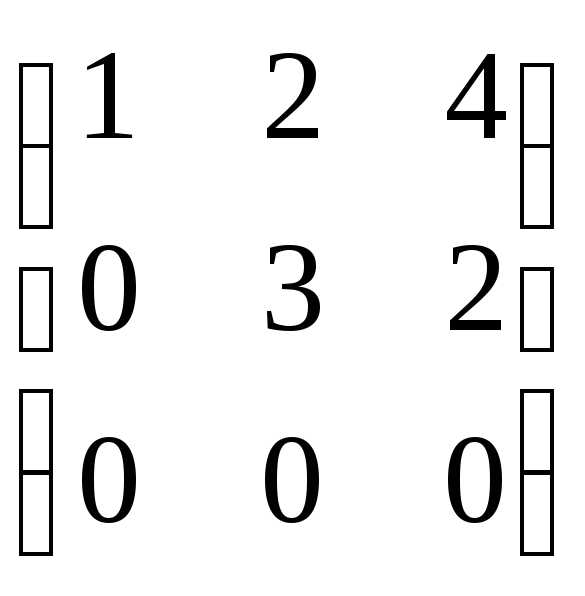
Составим матрицу системы: А=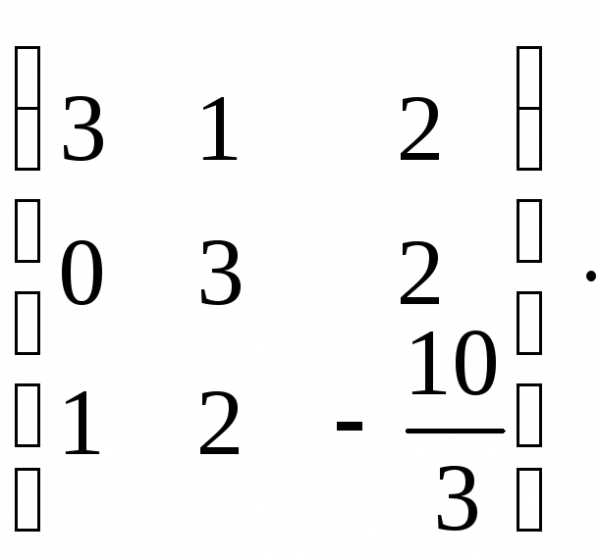
Приведем её к треугольному виду:
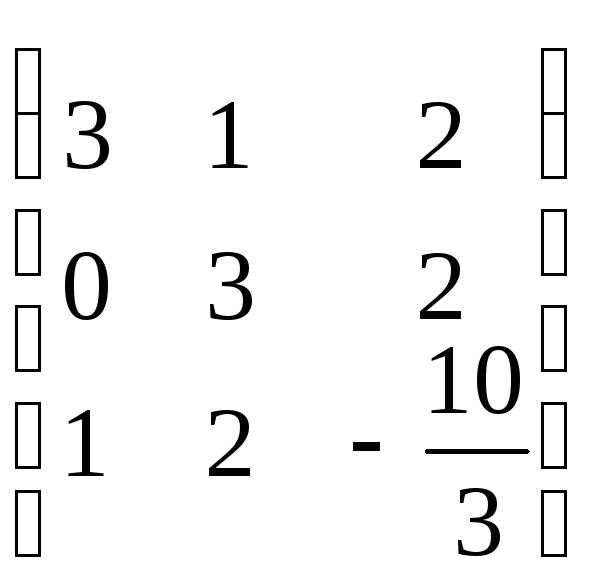

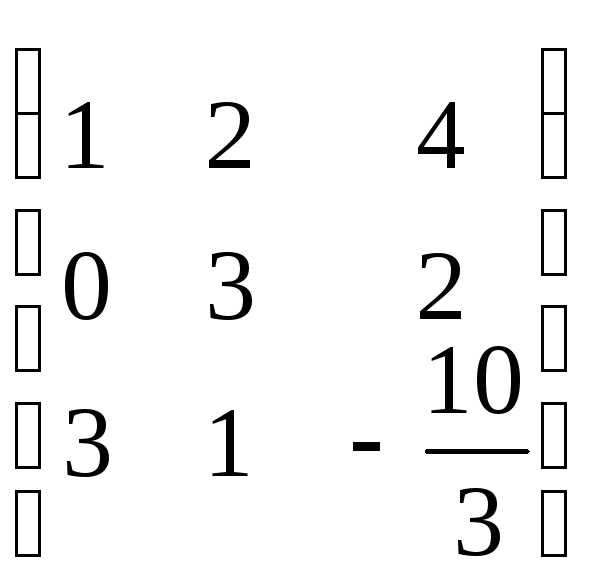
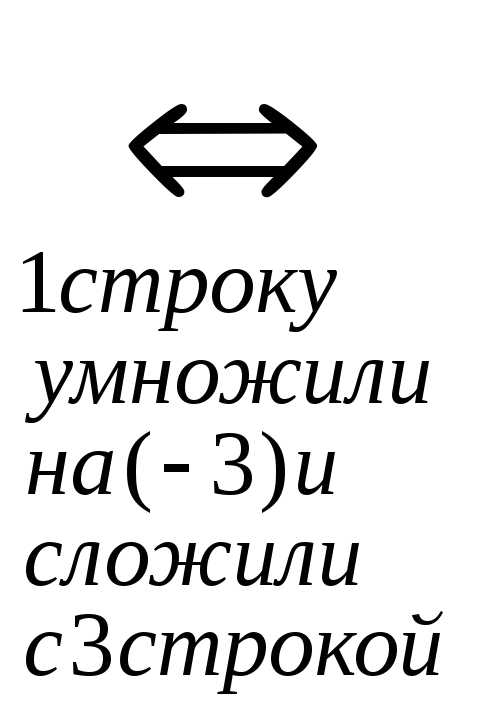
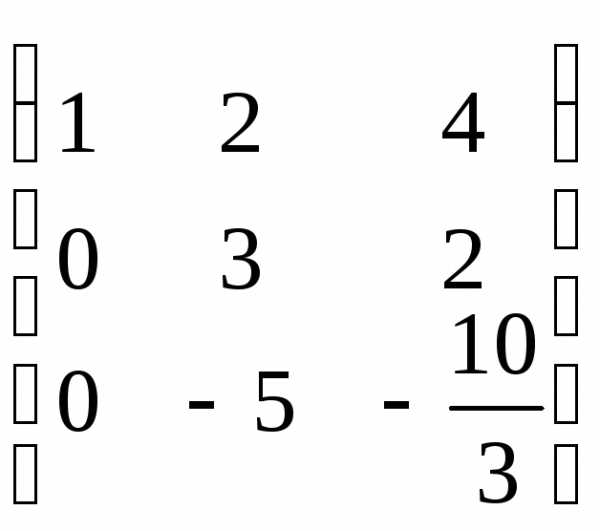
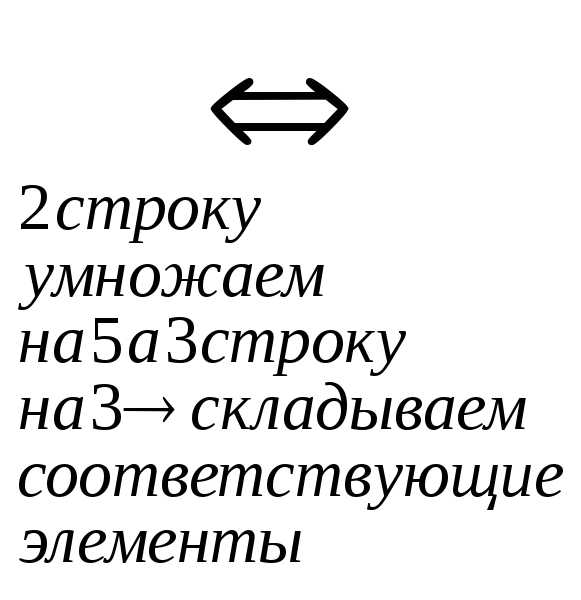
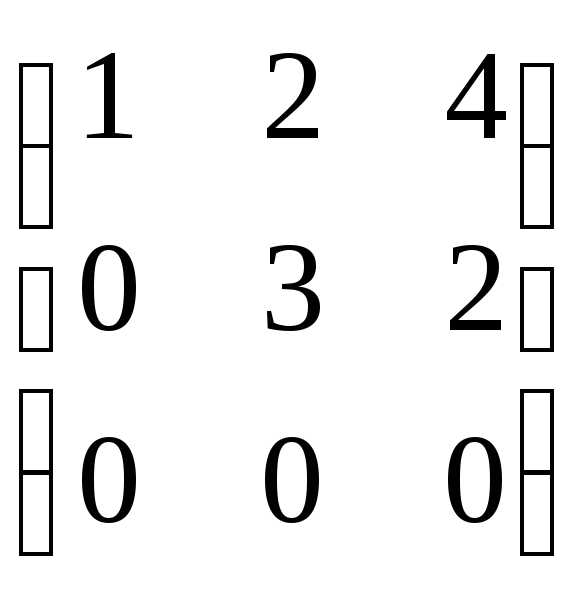
r(A)=2. Запишем эквивалентную систему уравнений: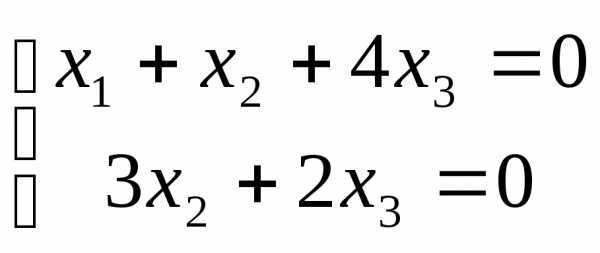
Примем за базисные переменные 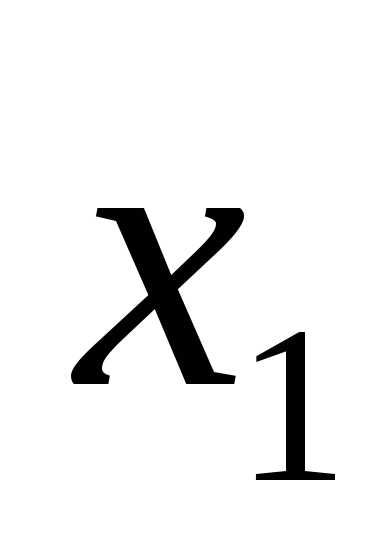 и
и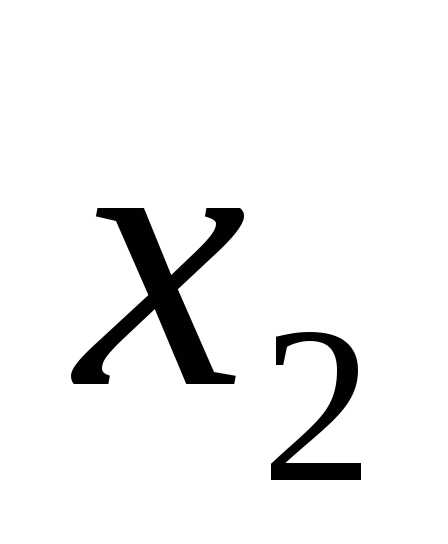 , а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (3-2)=1, т. е. у нас одна свободная переменная это
, а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (3-2)=1, т. е. у нас одна свободная переменная это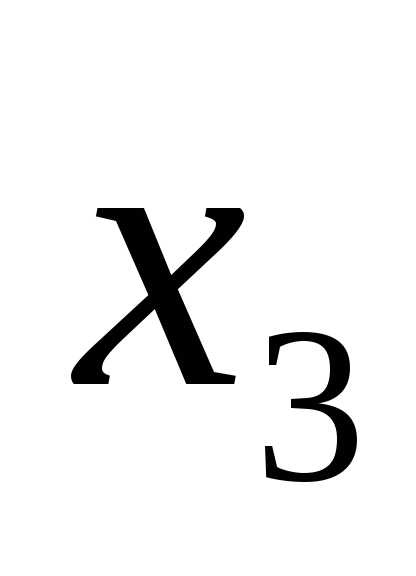 .
.
Выразим базисные переменные через свободные: 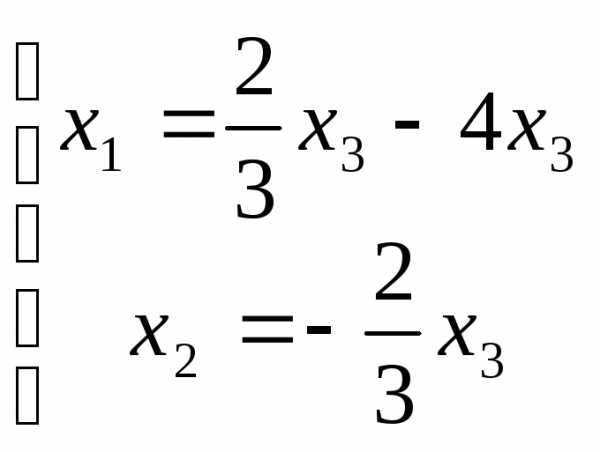

 . Обозначая свободную переменную:
. Обозначая свободную переменную: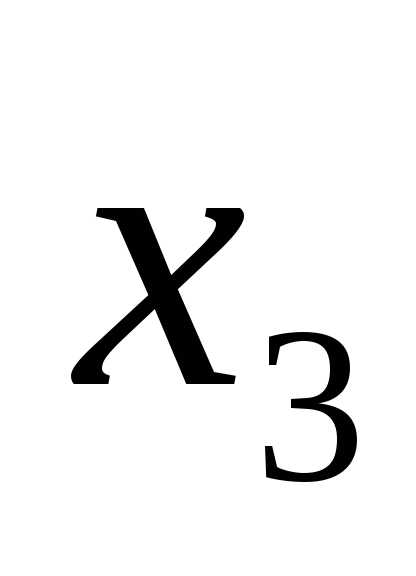 =
=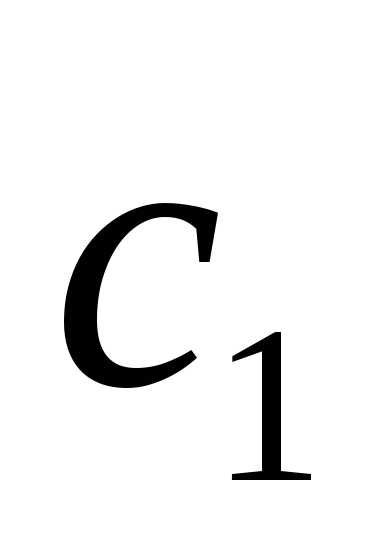 , получаем общее решение в виде:
, получаем общее решение в виде: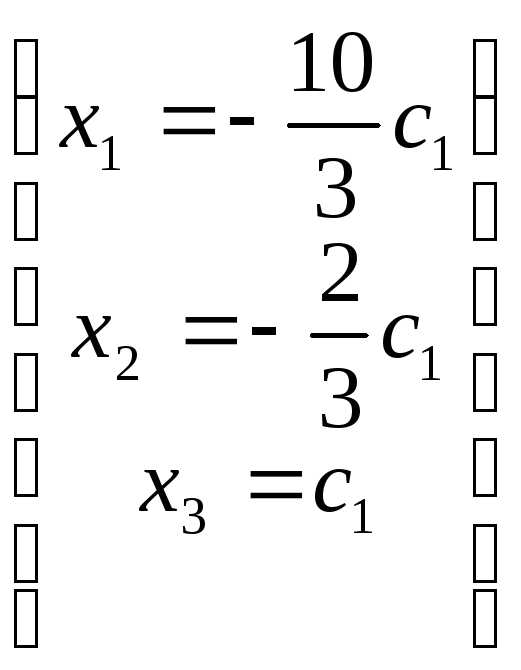
Пример 4.4
Найти общее решение системы: 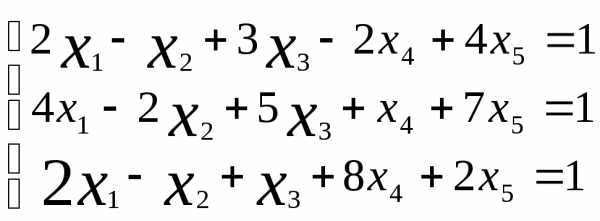
Решение.
Приведем расширенную матрицу системы к ступенчатому виду:
АВ= 


r(A)=r(AВ)=2<n, гдеn-число неизвестных, то система совместная и неопределенная. Запишем эквивалентную систему уравнений:
Примем за базисные переменные 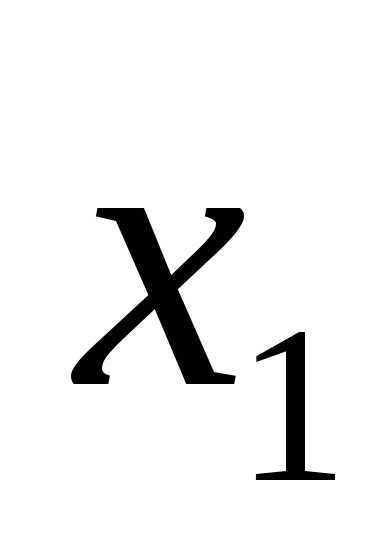 и
и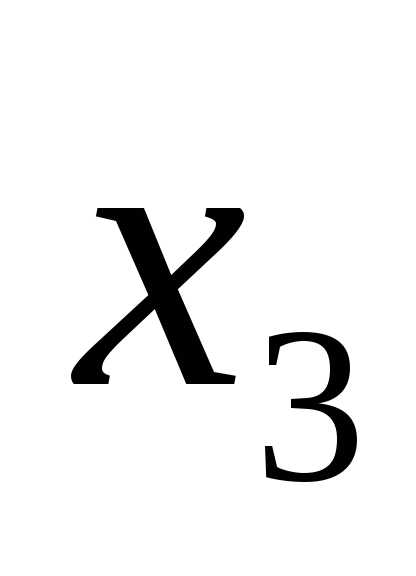 , а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (5-2)=3, значит
, а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (5-2)=3, значит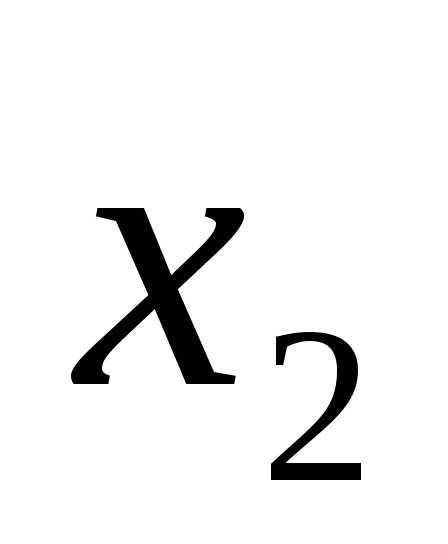 ,
,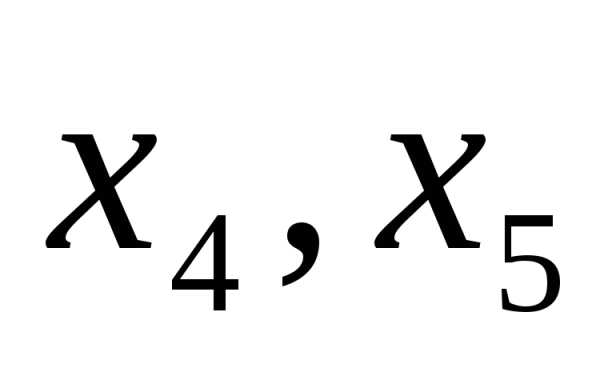 -свободные переменные.
-свободные переменные.
Выразим базисные переменные через свободные: 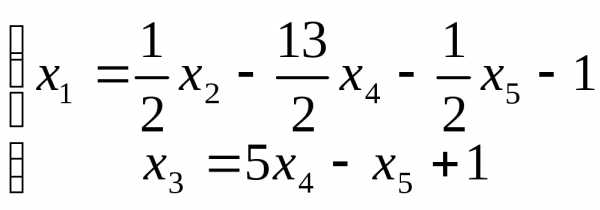 Обозначая свободную переменную:
Обозначая свободную переменную: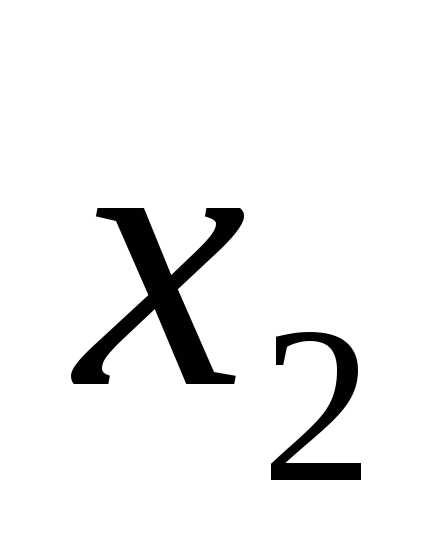 =
=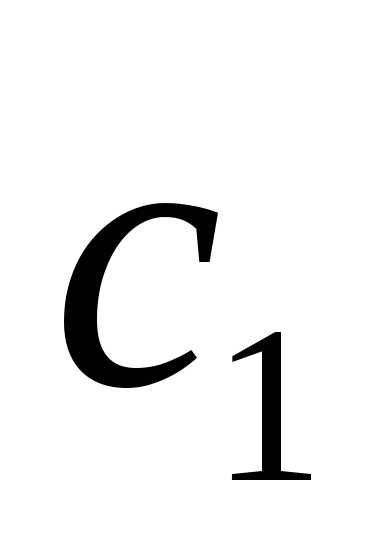 ,
,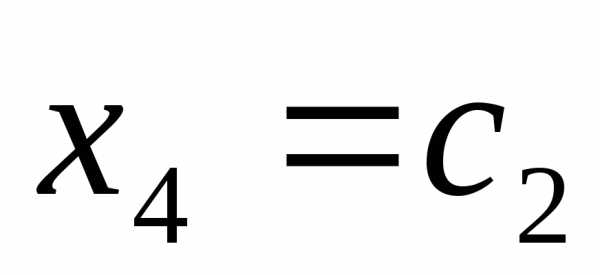 ,
,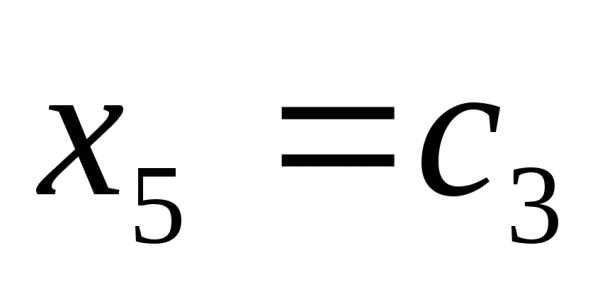 получаем общее решение в виде:
получаем общее решение в виде: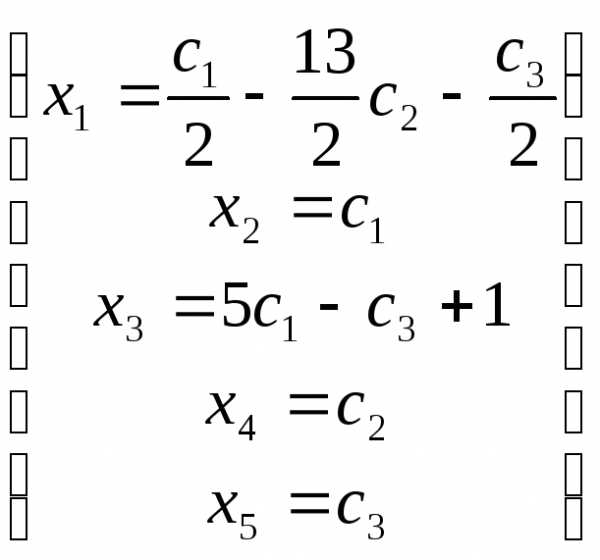 .
.
studfiles.net
Метод присоединенной матрицы
Количество просмотров публикации Метод присоединенной матрицы - 313
Определение обратной матрицы
ОБРАТНЫЕ МАТРИЦЫ
ЛЕКЦИЯ 3
Обратная матрица Метод присоединенной матрицы. Матричные уравнения. Матричный способ решения систем линейных уравнений. Ранг матрицы. Метод окаймляющих миноров. Метод элементарных преобразований. Теорема о базисном миноре.
Матрица А–1 принято называть обратной матрицей по отношению к матрице А, в случае если выполняется равенство
AA–1 = A–1A = E. (3.1)
Из данного определения следует, что взаимообратные матрицы перестановочны. Это означает, что только квадратные матрицы могут иметь обратные. При этом не каждая квадратная матрица имеет обратную. Для того чтобы матрица А имела обратную, крайне важно и достаточно, чтобы ее определитель был отличен от нуля: detA¹0.
% Действительно, из определения обратной матрицы и свойств определителей получаем: det(A–1A)=detA–1detA=detE=1, откуда следует крайне важно е условие существования обратной матрицы: detA¹0 или detA–1¹0. Вопрос о доказательстве достаточности этого условия несколько сложнее. Для этого нужно указать алгоритм построения такой матрицы. По этой причине мы вернемся к этому вопросу позднее (см. метод присоединенной матрицы).
Отметим, что если обратная матрица существует, то такая матрица только одна. Действительно, пусть существует еще одна матрица В, удовлетворяющая условию АВ=ВА=Е, тогда можно написать:
BAA–1=(BA)A–1=EA–1=A–1,
BAA–1=B(AA–1)=BE=B,
откуда получаем В=А–1, ᴛ.ᴇ. обратные матрицы совпадают. &
Матрица, определитель которой отличен от нуля, принято называть невырожденной, или неособенной; в противном случае она принято называть вырожденной, или особенной. Необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: обратная матрица существует, причем только одна, тогда и только тогда, когда исходная матрица невырожденная.
Стоит сказать, что для невырожденных матриц справедливы следующие свойства:
| 1) detA–1=(detA)–1, | 2) (AB)–1=B–1A–1, | 3) (AT)–1=(A–1)T, |
| 4) (A–1)–1=A, | 5) (An)–1=(A–1)n. |
Матрица AÚпринято называть присоединенной к матрице A, если она является транспонированной к матрице A, а вместо элементоввзяты их алгебраические дополнения, ᴛ.ᴇ.
Теорема 3.1. Обратная и присоединенная матрицы связаны соотношением
(3.2)
% Действительно, рассмотрим произведение матриц
При этом учтем, что сумма произведений элементов некоторой строки или столбца на их алгебраические дополнения равно определителю матрицы (см. теорему о разложении определителя по строке или столбцу).Дополнительно мы воспользуемся еще одним свойством определителей: сумма произведений алгебраических дополнений некоторой строки или столбца на соответствующие элементы другой строки или столбца равно нулю. Это связано с тем, что такая сумма эквивалентна определителю, у которого две одинаковые строки или столбца, и, следовательно, он будет равен нулю. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, перемножая рассматриваемые матрицы, получим
Отсюда следует справедливость приведенной теоремы. Более того, фактически мы указали алгоритм построения обратной матрицы при помощи присоединенной матрицы и тем самым доказали достаточное условие существования обратной матрицы. &
Общая схема нахождения обратной матрицы (метод присоединенной матрицы):
1) Вычисляем определитель заданной матрицы, в случае если он равен нулю, то обратной матрицы не существует.
2) Транспонируем заданную матрицу.
3) Вычисляем все алгебраические дополнения транспонированной матрицы.
4) Составляем присоединенную матрицу, ᴛ.ᴇ. вместо элементов транспонированной матрицы ставим их алгебраические дополнения.
5) Записываем обратную матрицу. Для этого каждый элемент присоединенной матрицы делим на определитель исходной матрицы.
6) Делаем проверку.
Пример 3.1. Найти A–1, если
Решение. 1) detA = –4.
2)
3) Ищем алгебраические дополнения транспонированной матрицы (не забывать учитывать знаки алгебраических дополнений!):
4) Составляем присоединенную матрицу:
5) Записываем обратную матрицу:
6) Делаем проверку: AA–1 = A–1A = E:
Следовательно, обратная матрица найдена правильно. à
Пример 3.2. Найти обратную матрицу
Решение. Поскольку
и A11 = d, A12 = –c, A21 = –b, A22 = a, то
Эту формулу можно использовать для нахождения обратных матриц второго порядка. à
referatwork.ru










