§ 9. Общий план исследования функций и построение графиков. Исследование графиков
Построить график функции y=f(x). Исследование функции онлайн.
Введите график функции
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно: a должно быть меньше b, иначе график не сможет построиться. Cледите за масштабом - если графика на рисунке нету, значит стоит поварьировать значения a и bПримеры
С применением степени(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)Квадратный корень
sqrt(x)/(x + 1)Кубический корень
cbrt(x)/(3*x + 2)С применением синуса и косинуса
2*sin(x)*cos(x)Арксинус
x*arcsin(x)Арккосинус
x*arccos(x)Применение логарифма
x*log(x, 10)Натуральный логарифм
ln(x)/xЭкспонента
exp(x)*xТангенс
tg(x)*sin(x)Котангенс
ctg(x)*cos(x)Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)Арктангенс
x*arctg(x)Арккотангенс
x*arсctg(x)Гиберболические синус и косинус
2*sh(x)*ch(x)Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
absolute(x) Абсолютное значение x(модуль x или |x|) arccos(x) Функция - арккосинус от xarccosh(x) Арккосинус гиперболический от xarcsin(x) Арксинус от xarcsinh(x) Арксинус гиперболический от xarctg(x) Функция - арктангенс от xarctgh(x) Арктангенс гиперболический от xee число, которое примерно равно 2.7 exp(x) Функция - экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) pi Число - "Пи", которое примерно равно 3.14 sin(x) Функция - Синус от xcos(x) Функция - Косинус от xsinh(x) Функция - Синус гиперболический от xcosh(x) Функция - Косинус гиперболический от xsqrt(x) Функция - квадратный корень из xsqr(x) или x^2 Функция - Квадрат xtg(x) Функция - Тангенс от xtgh(x) Функция - Тангенс гиперболический от xcbrt(x) Функция - кубический корень из xfloor(x) Функция - округление x в меньшую сторону (пример floor(4.5)==4.0) sign(x) Функция - Знак xerf(x) Функция ошибок (Лапласа или интеграл вероятности)В выражениях можно применять следующие операции:
Действительные числа вводить в виде 7.5, не 7,52*x - умножение 3/x - деление x^3 - возведение в степень x + 7 - сложение x - 6 - вычитаниеwww.kontrolnaya-rabota.ru
§ 9. Общий план исследования функций и построение графиков
Найти ОДЗ и точки разрыва функции.
Найти точки пересечения графика функции с осями координат.
Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
Найти асимптоты графика функции: а) вертикальные, b) наклонные.
На основании проведенного исследования построить график функции.
Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.
Примеры. Исследовать функции и построить их графики.
.
Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: x = 0,у=0.
Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).
. Критические точки: x1 = 1; x2= –1.
3.
а) Вертикальных асимптот нет
б) .
Асимптота – y = 0.
.
D(y)=(–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: .
.
а) Вертикальных асимптот нет
б).
Наклонных асимптот нет.
.
D(y)=(0; +∞). Функция непрерывна на области определения.
Пересечение с осью :
2.
3.
а) .
Вертикальная асимптота x = 0.
б).
Наклонная асимптота y = 0.
.
D(y)=( –∞;0)È(0;1)È(1;+∞).
Функция имеет две точки разрыва x= 0 и x= 1.
Точек пересечения с осями координат нет.
при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.
а
)
Вертикальные асимптоты x = 0, x = 1.
б)
Наклонная асимптота y = x + 1.
Раздел VI. Комплексные числа
§ 1. Основные понятия
Опр. 1. Комплексным числом называется выражение z=x+iy, (1) где х, у – действительные числа, а символ i – мнимая единица, которая определяется условием i2=-1. При этом число х называется действительной частью комплексного числа z и обозначается x=Rez, а у – мнимой частью z и обозначается Imz (от французских слов: reel – действительный, imaginare – мнимый). Выражение (1) называется алгебраической формой комплексного числа.
Опр. 2. Два комплексных числа z=x+iy и 
=x-iy, которые отличаются только знаком мнимой части, называются сопряжёнными.
Опр. 3. Два комплексных числа z1=x1+iy1 и z2=x2+iy2 считаются равными тогда и только тогда, когда равны их действительные и мнимые части:
§ 2. Операции над комплексными числами в алгебраической форме
Арифметические действия над комплексными числами, заданными в алгебраической форме, выполняются по обычным правилам действий над двучленами с учётом того, что i2=-1. Так, если z1=x1+iy1, z2=x2+iy2, то
1)
2)
3)
4)
studfiles.net
1. Исследование функций и построение графиков.
19
МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ И ПРОДОВОЛЬСТВИЯ УКРАИНЫ
ГОСУДАРСТВЕННЫЙ КОМИТЕТ РЫБНОГО ХОЗЯЙСТВА УКРАИНЫ
Керченский государственный морской технологический университет
Кафедра высшей математики и физики
ВЫСШАЯ МАТЕМАТИКА
Методические указания
по выполнению расчетно-графической работы раздела высшей математики
«Математический анализ»
( исследование функций и построение графиков, построение эмпирической формулы методом наименьших квадратов)
для студентов дневной формы обучения
специальности «Эксплуатация судовых энергетических установок»
направления 6.070104 «Морской и речной транспорт»
Керчь, 2009
Автор: Драчева И.А., ассистент кафедры высшей математики и физики КГМТУ
Рецензент: Моисеенко С.С., ст. преподаватель кафедры высшей математики и физики КГМТУ
Методические указания рассмотрены и одобрены на заседании кафедры высшей математики и физики КГМТУ,
протокол № от 2009 г.
Методические указания рассмотрены и рекомендованы к утверждению на заседании методической комиссии технологического факультета КГМТУ
протокол № от 2009 г.
Методические указания утверждены на заседании методического совета КГМТУ,
протокол №___ от _________2009 г.
© Керченский государственный морской технологический университет, 2009
Содержание
| Введение……………………………………………………………………… | 4 | |
| 1 | Исследование функций и построение графиков…………………………… | 5 |
| 1.1 | Определение функции. Основные характеристики……………………….. | 5 |
| 1.2 | Признаки монотонности функции…………………………………………. | 6 |
| 1.3 | Экстремумы функции……………………………………………………….. | 6 |
| 1.4 | Выпуклость вогнутость. Точки перегиба…………………………………… | 7 |
| 1.5 | Асимптоты……………………………………………………………………. | 8 |
| 1.6 | Общая схема исследования и построение графиков функции…………….. | 9 |
| 1.7 | Примеры выполнения РГР…………………………………………………… | 10 |
| 2 | Понятие об эмпирических формулах. Метод наименьших квадратов…… | 14 |
| 2.1 | Эмпирические формулы……………………………………………………... | 14 |
| 2.2 | Определение параметров линейной зависимости методом наименьших квадратов……………………………………………………………………… | 15 |
| 2.3 | Пример выполнения РГР…………………………………………………….. | 16 |
| Рекомендуемая литература………………………………………………….. | 18 |
Введение
Расчетно-графическая работа для студентов 1-го курса (I семестр 2-я четверть) специальности «Судовые энергетические установки» выполняется по следующим разделам математического анализа:
- приложение производной, исследование функций и построение графиков;
- функции нескольких переменных, построение эмпирической формулы методом наименьших квадратов.
В первом задании надо с помощью производной исследовать функции и поострить их графики, во втором задании методом наименьших квадратов составить эмпирическую формулу, выражающую зависимость между двумя величинами х иy .
В данных методических указаниях в краткой форме изложен теоретический материал по данным темам, разбираются решения подобных задач РГР. Методические указания должны помочь студентам в самостоятельном выполнении расчетно-графической работы, а также в подготовке к модульному и семестровому контролю.
Задания по РГР выдаются преподавателем, ведущим практические занятия по высшей математике. Расчетно-графическая работа должна быть выполнена студентом в отдельной тетради и сдана преподавателю на проверку. Работа выполняется аккуратно с подробным объяснением решения задачи. Студент должен защитить свою работу, решив подобную задачу или ответив на вопросы преподавателя по РГР.
Методические указания могут использоваться студентами других специальностей, как морского факультета, так и технологического.
Определение функции. Основные характеристики функций.
Если каждому значению переменной х из множестваХпо некоторому правилу поставлено в соответствие единственное вполне определенное значениеy,то переменнуюyназываютфункциейотх. Записываютили . Говорят ещё, что функция отображает множествоХна множествоY .
Множество Хназывается областью определения функции и обозначается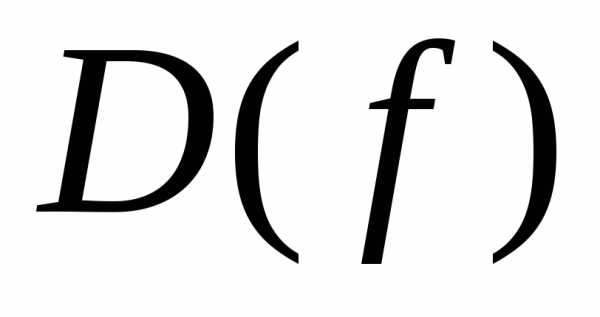
. Множество всех
называется множеством значений функции и обозначается
.х – независимая переменная величина или аргумент,y – функция или зависимая переменная.
Функция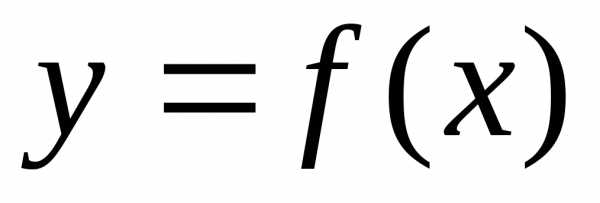 
, определенная на множестве
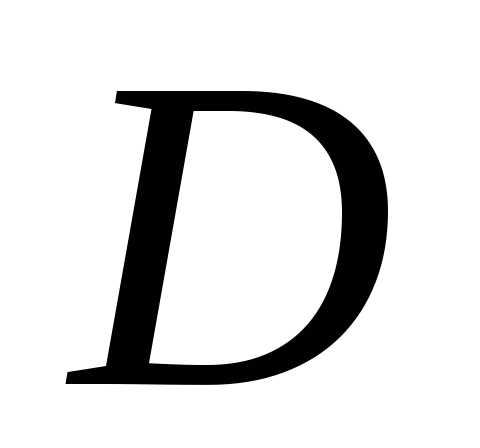называетсячетной, если для любого
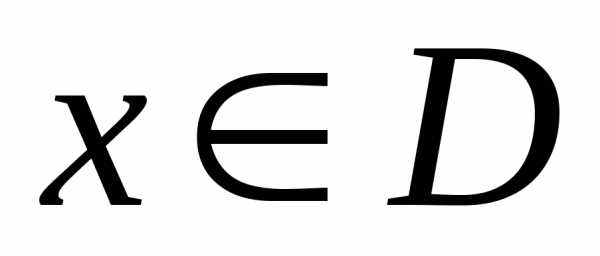выполняется условиеи;нечетной,если для любого
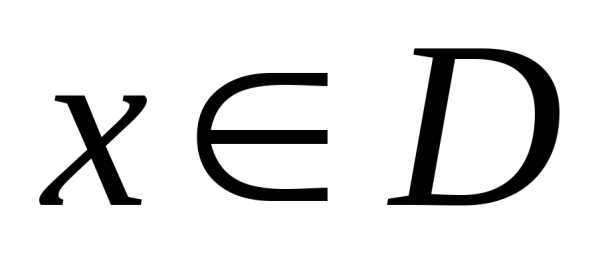выполняется условиеи.
График четной функции симметричен относительно оси Оy, нечетной – относительно начала координат.
Например: - четные функции; а- нечетные функции;- функции общего вида, т.е. не четные и не нечетные.
Функция называетсяпериодическойна множествеD, если существует такое числоТ>0, что при каждом значении
и. При этом числоТназываетсяпериодом функции.
Функция 
называетсявозрастающейв интервале
, если для любых двух точек
и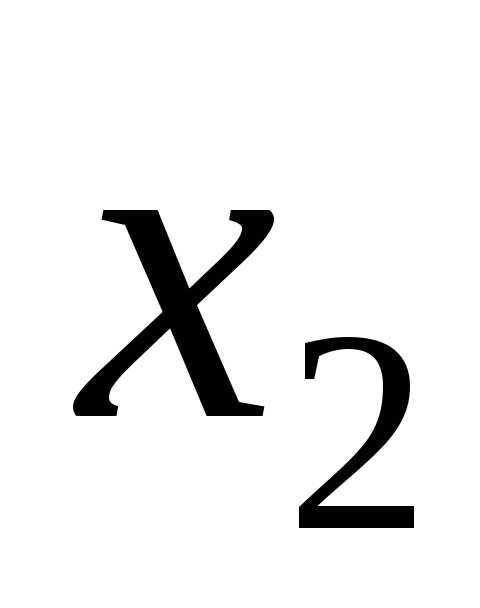
из указанного интервала, удовлетворяющих неравенству
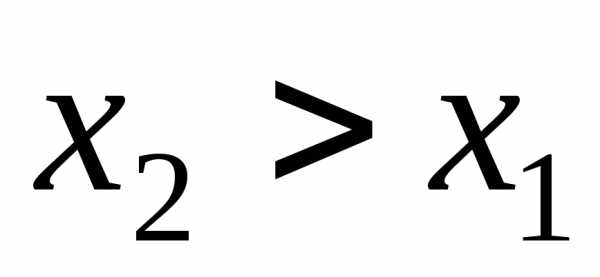, выполняется неравенство, если, функция называетсянеубывающей.
Иными словами – значения возрастающей функции увеличиваются одновременно со значением аргумента.
Функция 
называетсяубывающей в интервале
, если для любых двух точек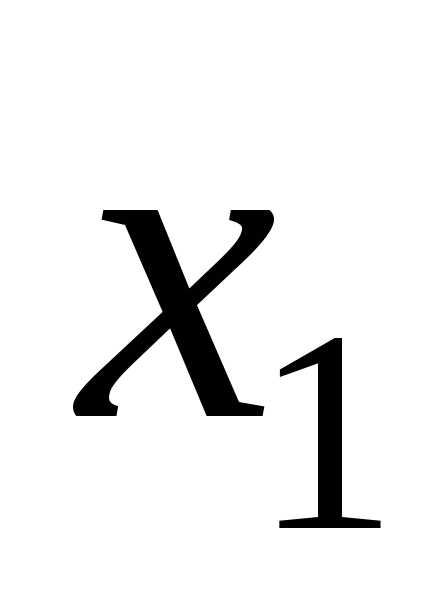
и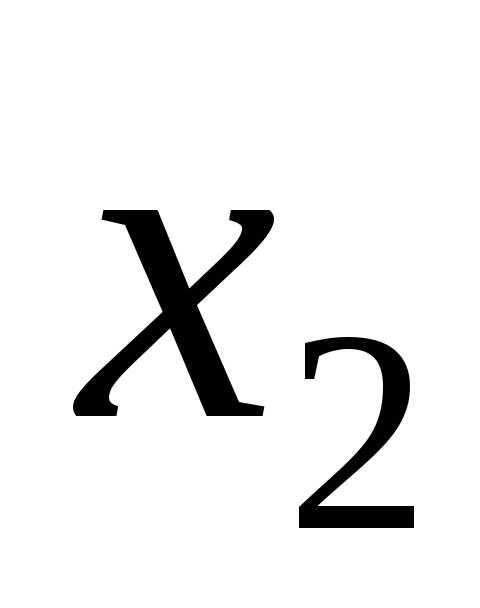
из указанного интервала, удовлетворяющих неравенству
, выполняется неравенство, если, функция называетсяневозрастающей.
Возрастающие, невозрастающие, убывающие и неубывающие функции называются монотонными. А возрастающие и убывающие –строго монотонными.
Функция, заданная графиком на рис. 1, убывает на интервале (-2; 1), не убывает на интервале (1; 3), возрастает на интервале (3; 5).
Признаки монотонности функции.
Если функция
дифференцируема на интервале
и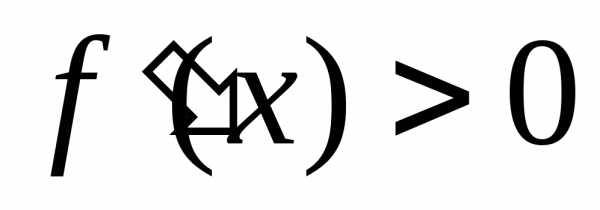
во всех точках интервала, то функция
возрастает на этом интервале.Если функция
дифференцируема на интервале
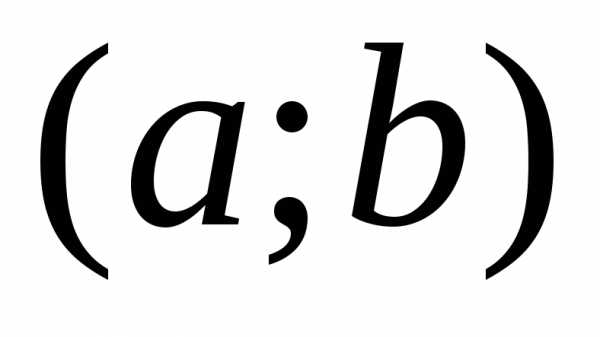и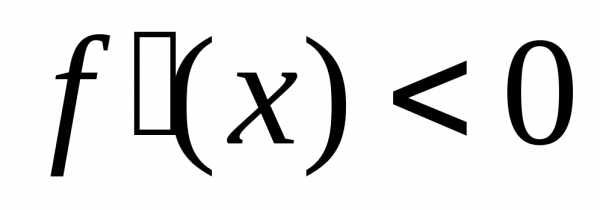
во всех точках интервала, то функция
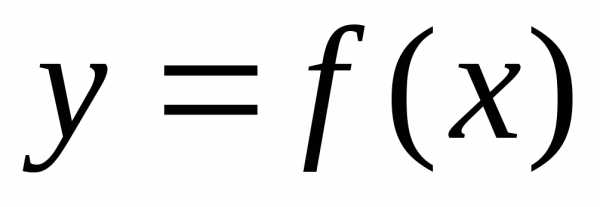убывает на этом интервале.Если
(
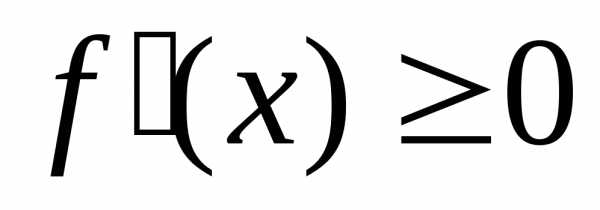) для всех точек интервала
, то функция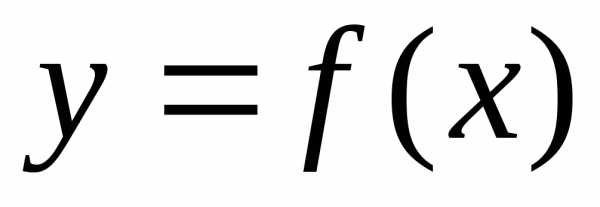
не убывает (соответственно, не возрастает) на этом интервале, т.е. для любых двух точек из интервала
из неравенства
следует(соответственно,).
1.3 Экстремумы функции.
Точка 
называетсяточкой максимумафункции
, если значение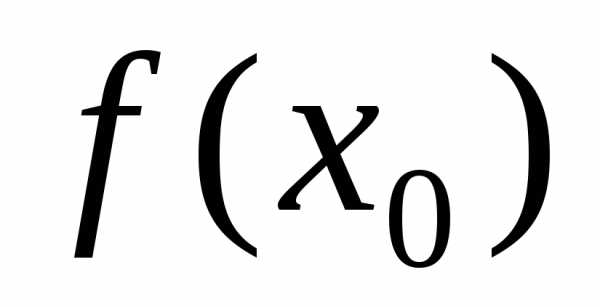
является наибольшим в некоторой окрестности этой точки.
Точка 
называетсяточкой минимумафункции
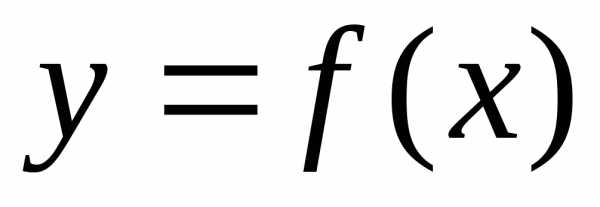, если значение
является наименьшим в некоторой окрестности этой точки.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках –экстремумами функции (рис. 2).
Теорема (Ферма – необходимое условие экстремума).Если
- точка экстремума для функции
, то в этой точке производная функции либо равна нулю, либо не существует.
Точки области определения функции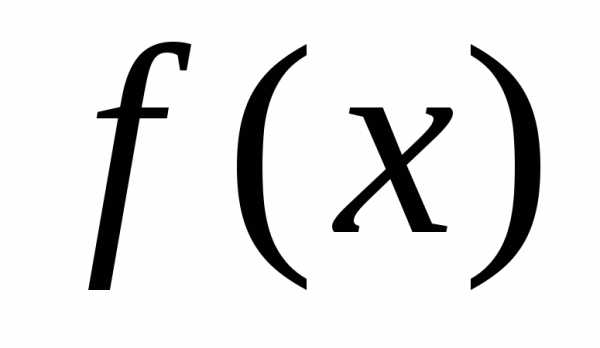 
, в которых ее производная не существует или равна нулю, называютсякритическими точкамифункции.
В силу теоремы Ферма экстремумы функции находятся среди ее критических точек.
Первое достаточное условие экстремума. Если при переходе (слева направо) через критическую точку
производная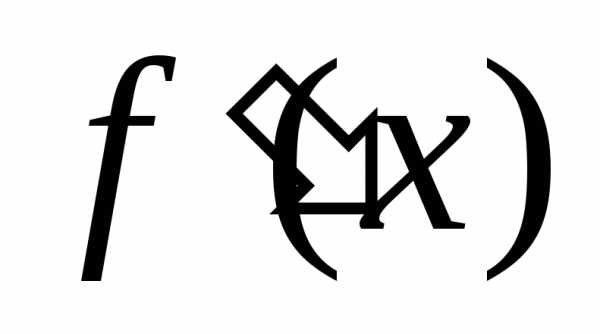
меняет знак с (+) на (-), то точка
является точкой максимума; если с (-) на (+), то точкой минимума; если знака не меняет, то экстремума нет.
Второе достаточное условие экстремума. Пусть в точке
производная равна нулю, а вторая производная. Тогда, если, то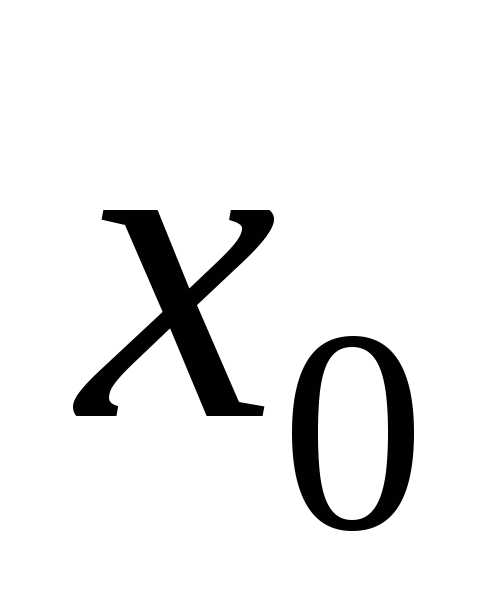
- точка минимума; если, то
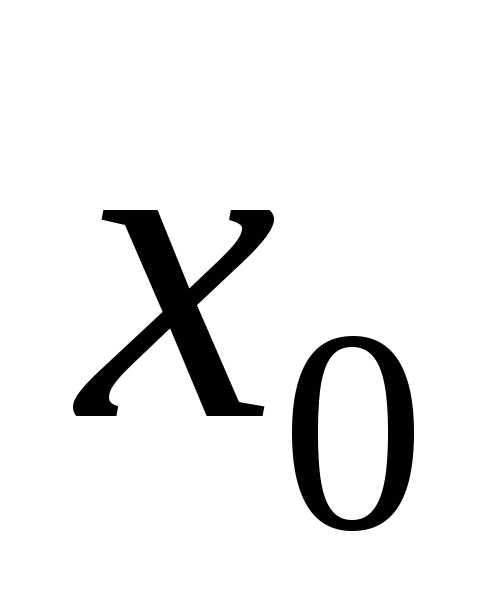- точка максимума.
studfiles.net
13. Общая схема исследования функций и построения графиков.
13.1 Общая схема исследования и построения графика функции заданной явно.
Общее исследование функции следует проводить по приведенной ниже схеме:
1.Определить область существования функции, область непрерывности, точки разрыва.
2. Найти асимптоты функции.
3. Выяснить вопрос о периодичности.
4. Выяснить вопрос о четности или нечетности.
В случае, если функция окажется четной или нечетнойдостаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
5.Найти точки пересечения графика функции с осями координат:
с осью абсцисс - точки , где-решение уравнения;
с осью ординат- точки , где.
6. Найти промежутки монотонности и локальные экстремумы.
7.Найти интервалы выпуклости и вогнутости, точки перегиба.
8. Составить таблицу
| Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | ||||
| знак | знак | знак | знак | ||||
| знак | знак | знак | знак |
Точки -все найденные в п.6-7 точки, в которых производные обращаются в нуль или не существуют.
9.На основании проведенного исследования построить график заданной функции.
Пример 26
Провести полное исследование и построить график функции .
Решение:
Область определения функции
Точка разрыва функции , функция непрерывна наи.
2. Асимптоты.
Вертикальная асимптота .
Поведение функции в окрестности :
Найдем наклонную асимптоту:
Прямая является наклонной асимптотой заданной кривой.
3. Функция не является периодической.
4. Четность функции
Условие четности или нечетности не выполнено. Заданная функция –функция общего вида.
5. Точки пересечения с осями.
График функции проходит через начало координат.
6. Промежутки монотонности, локальные экстремумы.
Найдем критические точки:
Исследуем знак производной методом интервалов:
знак
Найдем значения функции в критических точках:
7.Промежутки выпуклости и вогнутости. Точки перегиба.
Найдем вторую производную.
Точки, в которых равна нулю или несуществует:
Исследуем знак второй производной методом интервалов:
8. Составляем таблицу.
| 0 | - | ||||||
| + | 0 | + | - | - | 0 | + | |
| - | 0 | + | - | + | + | ||
| перегиб | разрыв | Мин. |
13.2 Общая схема исследования и построения графика функции заданной параметрически.
Функция задана параметрически
1.Исследовать область изменения ипри изменении параметра.
2. Найти значения параметра , при которыхи.
3.а)Найти значения параметра , при котрых. Найти вертикальную асимптоту
б) Найти значения параметра , при котрых. Найти наклонную асимптоту
,
4. Вычисляем и.Находим все значения параметра, при которых хотя бы одна из полученных производных обращается в нуль или терпит разрыв. Найденные значения параметра будем называть критическими.По формуле (9) определяем знак производнойв каждом из полученных интервалов.
5. Вычисляем вторую производную по формуле (16) или (17). Определяем значения параметрапри которыхобращается в нуль или терпит разрыв. Определяем промежутки выпукдости вогнутости согласно (40) и (41).
6. Строим таблицу
| Область изм. | Область изм. | Область изм. | Знак | Знак | Знак | Знак | Знак | Поведение |
7. Строим график функции.
Пример 27
Построить кривую (декартов лист), заданную параметрическими уравненниями:
Решение:
1.Обе функции определены при .
При этом
2.при
при .
3.а) При
При этом
Таким образом, вертикальных асимптот график функции не имеет.
б) Найдем наклонную асимптоту:
Таким образом, график функции имеет наклонную асимптоту:
4. Найдем производные и.
Найдем критические значения параметра
При обе производные терпят разрыв.
Таким образом, получаем следующие критические значения параметра :
Найдем по формуле (9):
5. Найдем :
6. Строим таблицу
| Область изм. | Область изм. | Область изм. | Знак | Знак | Знак | Знак | Знак | Поведение |
| убывает, вогнута | ||||||||
| убывает, вогнута | ||||||||
| возрастает, вогнута | ||||||||
| убывает, вогнута | ||||||||
| возрастает, выгнута |
7. Строим график
Задания 11. Провести полное исследование и построить график функции:
| 1. | 2. | 3. |
| 4. | 5. | 6. |
| 7. | 8. | 9. |
| 10. | 11. | 12. |
studfiles.net
Исследование функций методами дифференциального исчисления и построение графиков.
Решение.
1) Найдем область определения функции, интервалы непрерывности и точки разрыва функции:
Область определения: $x^2-1\neq 0\Rightarrow x\neq 1;\,\,\, x\neq -1$ $D(f)=(-\infty; -1)\cup(-1; 1)\cup (1; +\infty).$. Данная функция, как элементарная, непрерывная в каждой точке области определения. Точки $x=-1$ и $x=1$ - точки разрыва.
функция не является ни четной, ни нечетной.
Функция не периодичная.
Точка пересечения с осью Oy: .
Точка пересечения с осью Ox: $y=0\Rightarrow\frac{1}{x-1}=0.$ Следовательно, при всех из области определения. Т.е. кривая проходит через точку и не пересекает ось Ох.
2) Найдем асимптоты графика.
Вертикальные асимптоты могут быть в точках разрыва. Найдем односторонние пределы функции в этих точках.
. Таким образом, оба предела бесконечны и прямая является вертикальной асимптотой.
. Ни один из пределов не рамен бесконечности, то есть в этой точке асимптоты нет – в точке имеем устранимый разрыв.
Наклонные асимптоты задаются уравнением , где
.
Таким образом прямая - асимптота.
3) Вычислим производную функции и найдем ее интервалы монотонности и экстремумы.
Следовательно экстремумов функция не имеет.
|
x |
1 |
||
|
y' |
– |
Не существует |
- |
|
y
|
|
Не существует |
Производная всюду имеет знак «-». Следовательно, функция убывает на всей области определения.
4) Вычислим вторую производную и с ее помощью исследуем график на интервалы выпуклости и вогнутости и точки перегиба.
Следовательно, точек перегиба функция не имеет.
|
x |
1 |
||
|
y'' |
— |
не существует |
+ |
|
y |
не существует |
При , то есть функция выпукла вверх, При , то есть функция выпукла вниз.
5) Используя полученные данные, построим график.
kontrolnye.com
Анализ графиков. Базовые знания для любого трейдера
В каком бы сегменте финансового рынка вы ни работали, анализ графиков – лучший способ увидеть, как вела себя толпа на протяжении определённого времени. Причём время это может быть очень разным: хотите – увидите поведение за несколько минут, хотите – за пару десятков лет. А ведь именно толпа формирует цены, что бы там ни говорили – разумеется, за редким исключением.
Также по графикам можно легко просчитать предполагаемую прибыль; можно увидеть, где нужно закрыться, если вдруг прогноз не оправдается… Словом, это наилучший способ быстро оценить ситуацию на рынке. Чем, собственно, и занимается технический анализ.
Основные правила анализа графиков
Используя технический подход, трейдер автоматически принимает то, что здесь считается аксиомой: в графиках учтено абсолютно всё, каждый фактор. В этом можно сомневаться, что-то выяснять, но, если ваша цель заключается только в использовании чужих методов анализа и в успешной торговле, придётся согласиться. Или просто не углубляться мыслями в данную тему. Потому что веские аргументы есть и у сторонников данной теории, и у её противников. Тем не менее, во-первых, весь теханализ на этом базируется – отрицая то, что берётся за аксиому, вы отрицаете его полностью. А во-вторых, данный вид прогнозирования действительно работает, и это подтверждено не то что годами – веками.
Далее идут ещё две аксиомы. Вам нужно принять то, что цены стремятся к одному направлению. Именно это их свойство образует тренды и каналы на графиках. Толпа на время выбирает одно основное движение – вверх или вниз. А через какой-то промежуток направление будет изменено.
И последнее – «история повторяется». Разумеется, не в том смысле, что вы увидите совершенно одинаковые рисунки на графиках с одними и теми же котировками – нет. Но ценам свойственно задерживаться на одних и тех же уровнях, отскакивать от них. Это вы поймёте в процессе изучения графиков и теханализа.
Что должен понимать каждый трейдер
Глобальное видение рынка – первое, что отличает специалиста от дилетанта. Не пугайтесь – это вовсе не означает, что вам придётся читать экономическую литературу и смотреть новости трижды в день. Всё делается в рамках графического отображения цен.
Давайте подумаем, как обычно поступает среднестатистический трейдер-новичок? Узнав о том, что рынок можно анализировать, скажем, с помощью индикаторов RSI и Стохастик, он наносит их на график и ждёт сигналов, по которым будет открывать свои сделки. А ведь то, что он видит на экране – лишь малая часть того, что происходит на рынке. Допустим, используется таймфрейм Н1. И на нём есть некое направленное движение, хоть восходящее, хоть нисходящее, хоть боковое. Но ведь это лишь малая часть того, что есть сейчас в реальности на дневном графике. Потому что на самом деле значимый, казалось бы, тренд на Н1 может быть всего лишь коррекцией (возвратом цен) на D1. И, когда эта коррекция закончится, график развернётся. И для трейдера, который сам ограничил своё восприятие только таймфреймом Н1, данное событие будет внезапным.
Обычно достаточно – в рамках одной сделки – проанализировать только 1-2 временных периода выше того, который вы берёте для открытия позиций. Но если вы решили работать профессионально, не бегать в будущем с одной пары на другую, а просто выбрать несколько инструментов и торговать, то лучше сразу анализировать рынок глобально.
Предположим, вы решили взять для долгосрочной работы евро-фунт. Не обязательно это будет единственная пара – возможно, одна из многих, но сейчас посмотрим графики на её примере.
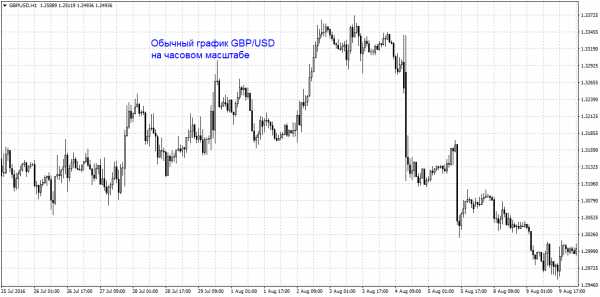
Начать стоит с самого крупного таймфрейма. Для пользователей МТ4 и большинства других терминалов это будет MN – график месячного изменения цен. Его, фактически, можно посмотреть один раз и возвращаться к нему всего несколько раз в год при необходимости. Он нужен нам, чтобы понять, что же происходит с котировками в целом.
На графике мы можем, не листая, видеть всю историю взаимодействия цен этих двух валют за последние более чем 20 лет. С 2001 по 2007 год наблюдался стабильный рост фунта против доллара. В 2007 цена достигла своего пика, после чего фунт с небольшой задержкой стремительно рухнул вниз – падение продолжалось в течение нескольких месяцев. Он упал даже ниже своего самого малого (на тот момент) исторического минимума. Несколько лет после этого – неопределённое состояние в целом, которое можно расценивать как рэндж. К июлю 2014 года цена поднялась до очень высокой на тот момент отметки и даже немного превысила её, но после опять начала снижение. На данный момент самый нижний исторический уровень пробит, продолжается падение фунта против доллара уже несколько месяцев. Нижняя граница текущего канала также пробита, что позволяет предполагать возможное дальнейшее снижение. В то же время цена на данный момент тестирует новый уровень, отмеченный красной горизонтальной линией. В какой-либо тренд котировки пока не вписываются. Это означает, что при открытии сделок трейдеру нужно быть осторожным, воздержаться пока от долгосрочных позиций, а на среднесрочных ставить жёсткие стоп-лоссы.
Если вы решите работать на валютной паре, где на данный момент подобная ситуация, то отслеживать таймфрейм MN желательно постоянно. Либо, по крайней мере, знать, какая цена является критичной – в данном случае это нижний исторический уровень, который пока не пробит. Также линия текущего канала и средняя горизонталь станут сопротивлением, если график пойдёт вверх.
Переключившись на таймфрейм W1, мы можем увидеть, что здесь текущую цену уже можно уместить в некие рамки, а именно – начертить небольшой канал. Тренд MN по-прежнему остаётся на графике и обозначен зелёным, а более мелкий канал, W1, выделен сиреневым цветом. Как видите, это всё тот же нисходящий тренд, только ускоренный. В данный момент цена находится на его верхней границе и даже пересекает её, хотя это нельзя считать уже сформировавшимся пробоем. Вариантов развития событий два. Если прорыва не произойдёт, и цена даст отскок вниз, то она пойдёт, как минимум, до нижней красной диагонали – исторического минимума. Если пробой всё-таки случится, то вполне возможна отработка фигуры «Двойное дно», которая уже сейчас чётко вырисовывается на графике, но пока не подтверждена.
Ситуация говорит о том, что на рынке в настоящее время большая неопределённость (именно на GBP/USD). Поэтому, если бы трейдер открывал свои сделки в рамках Н4, например, и совершенно не задумывался о том, что происходит в целом, то:
- Сначала он, возможно, получал бы прибыль.
- Затем с большой вероятностью он слил бы много денег в нескольких сделках из-за того, что ничего не знает об общем положении вещей.
Такие неопределённые ситуации, как то, что мы сейчас видим на фунт/долларе – лишь первая из причин, по которым нужно анализировать более масштабные графики. Вторая причина – то, что именно таким способом можно определить наиболее вероятное движение цены, чтобы открыть позицию на Н4 или D1. Это сделки с достаточно высоким для трейдера-новичка доходом, они существенно лучше и надёжнее, нежели скальпинг или торговля в течение всего нескольких часов. В то же время, это не долгосрочные позиции, где придётся долго ждать завершения. Но и для них метод хорош.
Не всегда ситуация на рынке бывает под вопросом. Нередко и MN, и W1, и D1 показывает сигналы в одном и том же направлении, и это означает, что вероятность успешной сделки возрастает втрое. Вам остаётся только найти точку входа.
Дополнительные особенности
Чтобы получить больше информации о вероятном движении цен в ближайшее время, используйте дополнительные инструменты анализа на крупных таймфреймах. Подойдут уровни Фибоначчи, японские свечи или индикаторы. Но применять лишь то, что вы уже лично протестировали на выбранном сочетании пары и таймфрейма. Это очень важно, потому что на крупных временных периодах большее значение имеют экономические события, чем, например, индикаторы.
Также осознайте, что анализ крупных масштабов даёт очень многое трейдеру, но будет совершенно бесполезен в том случае, если вы не освоите хотя бы самые основы графического прогнозирования. Без него невозможно оценить, что вообще происходит с ценами.
Также важно выставлять стоп-лоссы и соблюдать хотя бы на основном уровне мани-менеджмент. И, конечно, иметь свою тактику действий, пусть самую простенькую, но проверенную и в целом прибыльную.
Что делать скальпинг-трейдерам?
Если вы предпочитаете скальпинг, то наверняка задались вопросом, зачем вам всё это надо и надо ли вообще. Действительно, если трейдер торгует на 5-минутках, то ему не важно, что происходит на крупных таймфреймах. Но лишь при условии, что он всегда выставляет стоп-лосс. Если нет, то выбирайте: либо s/l, либо углубленный анализ. Иначе можно остаться без депозита, просто отлучившись на полдня от компьютера…
Также скальпинг-трейдерам имеет смысл применить эти правила в рамках своего «микромира» Форекс. Для них 5-15-минутные графики – то же, что для большинства – часовые и 4-часовые. Поэтому смело можно переключаться на 1-3 таймфрейма выше и анализировать, что же там происходит. Поверьте, это убережёт вас от ненужных сделок и улучшит ваши показатели в торговле в несколько раз.
tradingfin.com
Исследование функций и построение графиков
Количество просмотров публикации Исследование функций и построение графиков - 90
Полное исследование функции для построения ее графика включает следующие пункты (не обязательно именно в данном порядке).
1) Область определения функции (ООФ) и область ее значений (ОЗФ).
В случае если область определения функции не задана специально, то считают, что она совпадает с областью допустимых значений ее аргумента͵ ᴛ.ᴇ. с множеством всех точек х, для которых выполнима операция f. При нахождении ООФ используют ООФ элементарных функций , , , и др.
Область значений функции находят только в случаях, когда ее можно сразу указать, опираясь на свойства элементарных функций, к примеру, для функции , очевидно, .
2) Четность функции, ее периодичность.
Для установления четности (нечетности) функции , имеющей симметричную область определения, проверяют справедливость равенств ( ) для всех ООФ.
В случае четности или нечетности функции исследование ее поведения и построение графика можно проводить только для , а затем достроить график, используя симметрию: для четной функции график симметричен относительно оси OY, а для нечетной – относительно начала координат.
Для установления периодичности функции проверяют справедливость равенства для ООФ, где Т определяется видом функции. В случае периодической функции исследование проводят для одного промежутка периодичности.
3) Непрерывность функции, точки разрыва, вертикальные асимптоты.
Для определения промежутков непрерывности функции используют непрерывность базовых элементарных функций. В точках, ʼʼподозрительныхʼʼ на разрыв (отдельных точек, не входящих в ООФ), проверяют выполнение условий непрерывности. В случае если функция терпит разрыв в точке х0, то определют тип разрыва.
В случае если функция имеет бесконечный разрыв в некоторой точке х0, то прямая х = х0 является вертикальной асимптотой графика функции. В случае если только один из односторонних пределов при х0– 0 или х0+ 0 является бесконечным, то асимптота принято называть односторонней.
В случае если функция определена не на всей числовой оси, то крайне важно вычислить односторонние пределы функции в точках, ограничивающих промежутки ООФ. В случае если односторонний предел функции в точке а, ограничивающей промежуток ООФ, бесконечен, то х = а является односторонней вертикальной асимптотой графика функции. К примеру, в случае если ООФ: , то нужно найти ; если данный предел окажется бесконечным, то х = а является односторонней вертикальной асимптотой графика функции.
4) Промежутки монотонности и экстремумы.
Для определения промежутков монотонности функции используют достаточный признак монотонности.
Достаточный признак монотонности дифференцируемой функции:
если на интервале хÎ(а, b) производная сохраняет знак, то функция сохраняет монотонность на этом интервале, а именно: если , то f(x) возрастает, в случае если , то f(x) убывает.
Для установления точек экстремумов функции используют необходимый и достаточные признаки существования экстремума.
Необходимое условие существования экстремума функции: если непрерывная функция имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
Точки, принадлежащие ООФ, в которых производная равна нулю или не существует, называют критическими точками функции по ее первой производной (точками, ʼʼподозрительными на экстремумʼʼ).
Первый достаточный признак существования экстремума: если при переходе через критическую точку х0 (слева направо) производная изменяет свой знак, то в точке х0 есть экстремум причем это максимум, в случае если знак меняется с плюса на минус, и это минимум, в случае если знак меняется с минуса на плюс. В случае если при переходе через критическую точку х0 производная не изменяет свой знак, то в точке х0 нет экстремума функции .
Второй достаточный признак существования экстремума: если – дважды дифференцируемая функция в точке х0 и , тогда: если , то х0 – точка минимума функции, а если , то х0 – точка максимума.
Стоит сказать, что для нахождения точек экстремумов функции сначала находят критические точки по первой производной. После этого проверяют выполнение в них достаточных условий существования экстремума функции.
5) Промежутки выпуклости, вогнутости графика и точки перегиба.
Дуга кривой L принято называть выпуклой, в случае если все ее точки расположены не выше касательной, проведенной в любой точке этой дуги (рис. 27), и принято называть вогнутой, в случае если все ее точки расположены не ниже касательной, проведенной в любой точке дуги кривой.
Точки, принадлежащие кривой, и отделяющие участки выпуклости от участков вогнутости, называются точками перегиба кривой (рис. 27).
Достаточное условие выпуклости, вогнутости графика функции:если функция является дважды дифференцируемой и ее вторая производная сохраняет знак при всех xÎ(a;b), то график функции имеет постоянное направление выпуклости на этом интервале: при <0 – выпуклость вверх, при >0 – вогнутость (выпуклость вниз).
Необходимое условие для точки перегиба: если х0 – абсцисса точки перегиба графика функции , то ее вторая производная в этой точке равна нулю или не существует.
Точки, принадлежащие графику функции , в которых или не существует, называются критическими точками функции по ее второй производной (точками, ʼʼподозрительными на перегибʼʼ).
Достаточное условие для точек перегиба: если вторая производная при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. В случае если не изменяет знак при переходе через точку х0, то перегиба нет.
При нахождении промежутков выпуклости, вогнутости графика функции сначала находят критические точки по второй производной, после этого выделяют промежутки знакопостоянства второй производной на ООФ: если , то кривая вогнутая, а если , то кривая выпуклая. Точки перегиба определяют, используя достаточные условия перегиба.
6) Наклонные и горизонтальные асимптоты.
Асимптотой кривой, имеющей бесконечную ветвь, принято называть прямая, расстояние до которой от текущей точки М кривой стремится к нулю при удалении точки М от начала координат (рис. 28).
В случае если график функции имеет наклонную асимптоту с уравнением , то параметры k и b в уравнении асимптоты можно найти по формулам:
, (26)
. (27)
В случае если хотя бы один из этих пределов является бесконечным или не существует, то наклонных асимптот нет. В случае, когда k = 0, график имеет горизонтальную асимптоту с уравнением y = b.
В некоторых случаях (как правило, в случае если f(x) выражена через показательную или логарифмическую функцию), график может иметь асимптоты только при или только при .
Иногда ветви графика при и при имеют разные асимптоты.
7) Точки пересечения графика с осями координат или другие дополнительные точки графика.
Дополнительные точки графика находят в случаях, когда недостаточно информации для выбора масштаба по осям координат, ᴛ.ᴇ. когда на некотором промежутке ООФ нет ни точек экстремумов, ни точек перегибов, ни точек пересечения графика с осями координат.
Первообразная и неопределенный интеграл. Таблица интегралов
Функция F(x) принято называть первообразной для функции f(x) на интервале (a, b), в случае если для всех x из этого интервала выполняется равенство
. (1)
Неопределенным интегралом от функции f(x) принято называть множество всех первообразных этой функции, то есть неопределенный интеграл - ϶ᴛᴏ выражение вида , где .
Процедуру нахождения неопределенного интеграла называют интегрированием. При интегрировании используют: таблицу интегралов (таблица 2), свойства интегралов и специальные методы интегрирования, основные из которых – замена переменной и интегрирование по частям.
Таблица базовых неопределенных интегралов.
referatwork.ru
