Содержание
Схема развязок ЗСД — ЗСД СПб
Все развязки ЗСД достаточно сложны для понимания с первого раза. Поэтому для корректного движения по ним рекомендуется предварительно изучить схему проезда. Ниже будут показаны все развязки. Особое внимание следует обратить на то, что некоторые из развязок имеют несколько уровней.
Все развязки ЗСД
Схема пересечения с Зеленогорским и Скандинавским шоссе
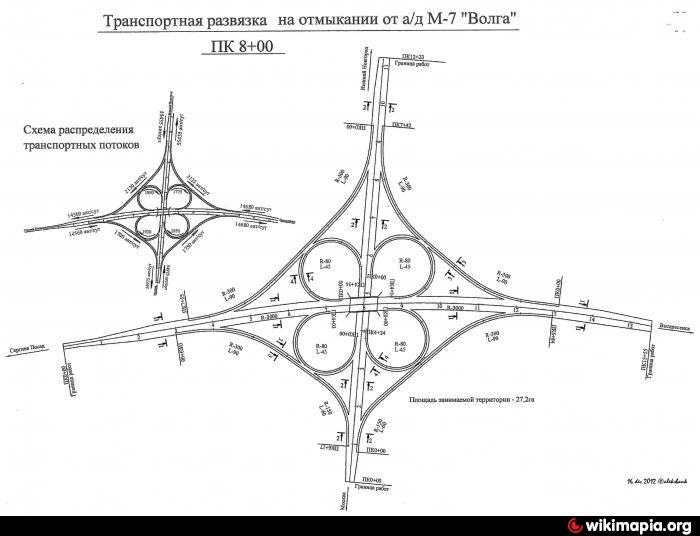
Схема пересечения с Новым шоссе
Схема пересечения с КАД и Левашовским шоссе
Схема развязки с Богатырским проспектом
Схема развязки с Приморским шоссе и ул. Савушкина
Схема развязки с проспектом Крузенштерна
Схема развязки с набережной реки Екатерингофки
Схема развязки с ул. Благодатная
Схема развязки с ул. Автомобильная, Краснопутилковская и Ленинским проспектом
Автомобильная, Краснопутилковская и Ленинским проспектом
Схема развязки с КАД, Дачным проспектом и Предпортовой улицей
Все карты ИНТЕРАКТИВНЫЕ, приблизьте их и вы увидите направления движения.
Вся трасса поделена на 3 участка — северный, центральный и южный, каждый из них имеет свои развязки.
Северный участок:
- Развязка с Зеленогорским и Скандинавским шоссе
- Развязка с Новым шоссе
- Развязка с КАД
- Развязка с Богатырским проспектом
- Развязка с Приморским шоссе и ул. Савушкина
Планируется: на пересечении Шуваловского проспекта и улицы Планерная сделать дополнительную развязку.
Центральный участок:
- Развязка на пересечении с проспектом Крузенштерна
Южный участок:
- Развязка с набережной реки Екатерингофки
- Развязка на ул. Благодатная
- Развязка с ул. Автомобильная, Краснопутилковская и Ленинским проспектом
- Развязка с КАД, Дачным проспектом и ул.
 Предпортовая
Предпортовая
Планируется: к 2022г соединить ЗСД со Шкиперским протоком, а в 2024г соеидинить с Витебским проспектом.
Схема пересечения с Зеленогорским и Скандинавским шоссе
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Санкт‑ПетербургСанкт‑Петербург — Яндекс.Карты
Схема пересечения с Новым шоссе
Развязка у Белоострова, открытая в сентябре 2019г поможет быстрее попасть на Приморское шоссе и далее в Курортный район. Жители Сертолово, посёлков Песочный и Левашово получили возможность удобного выезда на ЗСД, что по сравнению с загруженным выездом через Выборгское шоссе сократит путь в центр на 30 минут. Для тех жителей, которые уже сейчас используют ЗСД, протяжённость поездки сократится на 12 км.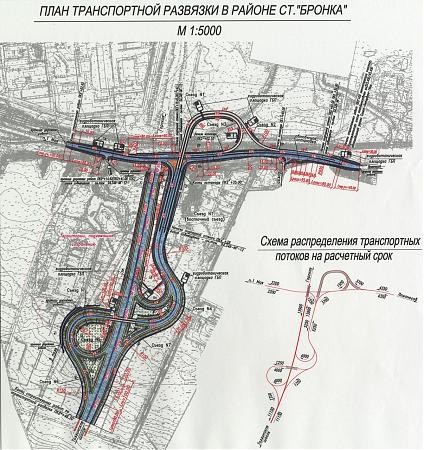
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
| — |
Развязка также позволит снять нагрузку с Выборгского шоссе в местах пересечения с Горским шоссе, Приозерским шоссе и Песочным шоссе. На ЗСД ожидают дополнительно 10 тысяч машин благодаря новой развязке.
Схема пересечения с КАД и Левашовским шоссе
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
| — |
Схема развязки с Богатырским проспектом
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Схема развязки с Приморским шоссе и ул.
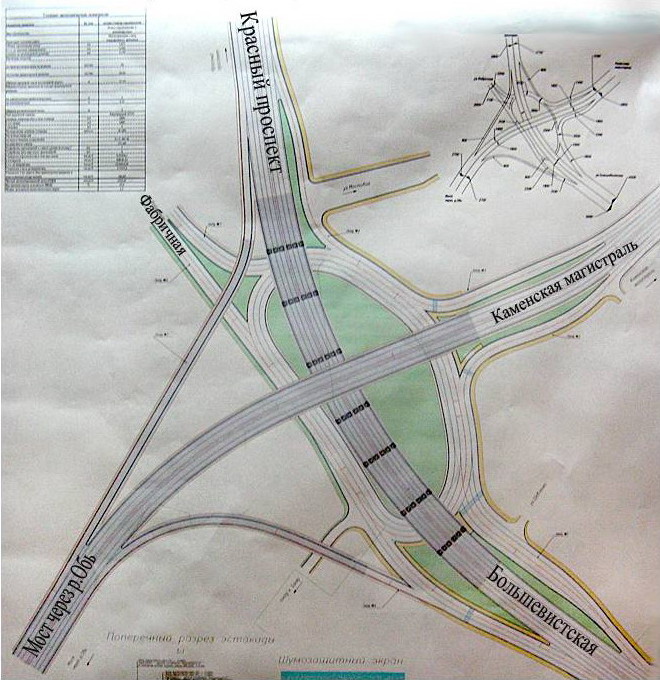 Савушкина
Савушкина
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Как съехать с ЗСД на Крестовский остров: съехать на Приморский проспект, далее проехать около 4км до Ушаковского моста. Проедите Большую Невку, Малую, далее свернете на Песочную набережную. Едите до Большого Крестовского моста.
Схема развязки с проспектом Крузенштерна
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Схема развязки с набережной реки Екатерингофки
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Чтобы с Обводного канала попасть на ЗСД в сторону Богатырского, вам нужно заехать на набережную реки Екатерингофки.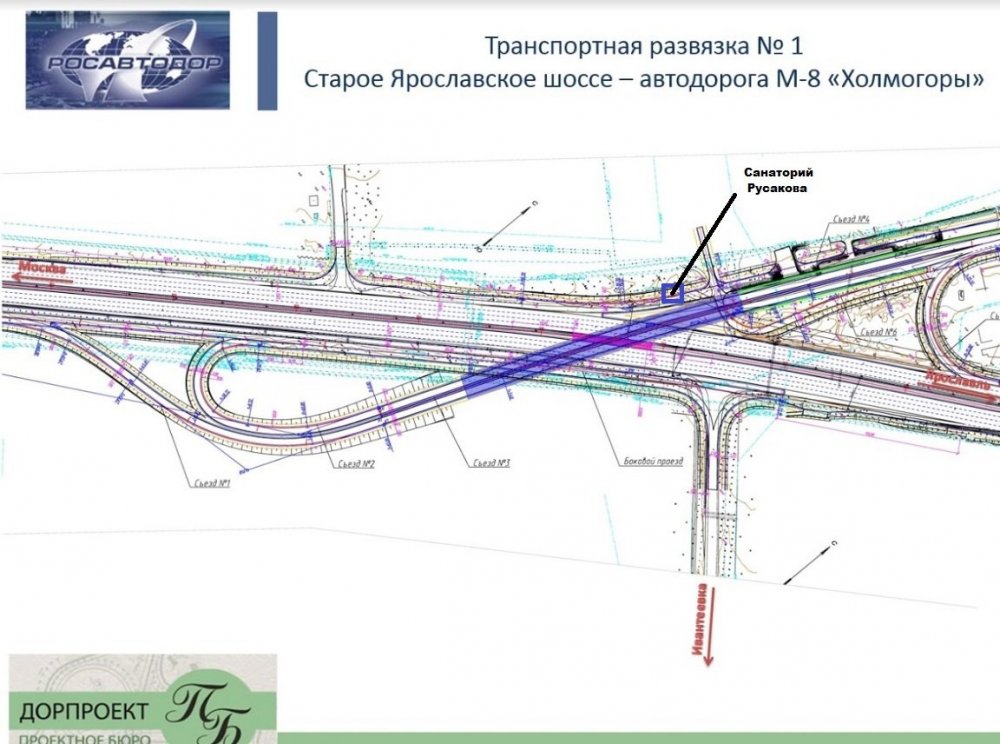
Схема развязки с ул. Благодатная
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Схема развязки с ул. Автомобильная, Краснопутилковская и Ленинским проспектом
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Схема развязки с КАД, Дачным проспектом и Предпортовой улицей
| Въезд/съезд | Соседние улицы и трассы | Крупные объекты рядом |
|
|
|
Развязки КАД Санкт-Петербурга 2023, схема кольцевой автодороги СПб
Развязки КАД Санкт-Петербурга 2023, схема кольцевой автодороги СПб — Karta-Ltd.ru
С картой найди дорогу! |
| ||
«КАРТА ТД» КАРТОГРАФИЧЕСКОЕ ИЗДАТЕЛЬСТВО |
| ||
+7 (812) 571-9350 |
Новинки | ||
Внимание! Уважаемые покупатели!
| |||
|
Информация по организации движения на развязках Санкт-Петербургской кольцевой автодороги дана по состоянию на 2023 год.
Ремонт КАД 2023
| |||
| |||
|
Издания, содержащие схемы развязок КАД
| ||
|
| |||
|
| |||
Схема развязки по току трехфазного инвертора с комплексным регулятором коэффициентов
- Чжэн, Синьсинь
- Сюй, Цзяньцзюнь
- Ши, Цзинкуй
- Хуан, Вэньсинь
- Ли, Циюэ
;
;
;
;
Аннотация
При управлении трехфазной системой сигналы переменного тока всегда преобразуются в сигналы постоянного тока путем синхронного преобразования координат. Предложена схема управления развязкой в синхронной системе отсчета dq (SRF) для реализации развязки по активному и реактивному току трехфазного инвертора. Комплексная модель борьбы с переносчиками установлена в SRF. В отличие от модели, установленной в статической системе отсчета, модель управления SRF может отражать характеристику связи активного и реактивного тока. В результате ПИ-регулятор с комплексным коэффициентом может применяться для реализации развязки по току. В данной работе анализируется характеристика связи трехфазной системы. Предлагается новый метод проектирования комплексного ПИ-регулятора на основе модели управления SRF, и рассчитываются коэффициенты. И дана его реализация в контуре управления. По сравнению с существующими ПИ-регуляторами с действительными или комплексными коэффициентами, предлагаемый комплексный ПИ-регулятор может полностью реализовать развязку активного и реактивного тока в трехфазной системе. Кроме того, схема управления может заставить токовую петлю соответствовать ожидаемой симметричной полосе пропускания, чтобы реализовать более высокую эффективную частоту отсечки.
Предложена схема управления развязкой в синхронной системе отсчета dq (SRF) для реализации развязки по активному и реактивному току трехфазного инвертора. Комплексная модель борьбы с переносчиками установлена в SRF. В отличие от модели, установленной в статической системе отсчета, модель управления SRF может отражать характеристику связи активного и реактивного тока. В результате ПИ-регулятор с комплексным коэффициентом может применяться для реализации развязки по току. В данной работе анализируется характеристика связи трехфазной системы. Предлагается новый метод проектирования комплексного ПИ-регулятора на основе модели управления SRF, и рассчитываются коэффициенты. И дана его реализация в контуре управления. По сравнению с существующими ПИ-регуляторами с действительными или комплексными коэффициентами, предлагаемый комплексный ПИ-регулятор может полностью реализовать развязку активного и реактивного тока в трехфазной системе. Кроме того, схема управления может заставить токовую петлю соответствовать ожидаемой симметричной полосе пропускания, чтобы реализовать более высокую эффективную частоту отсечки. В результате инвертор может достигать хороших динамических характеристик. Наконец, результаты моделирования и эксперимента приведены для проверки теоретического анализа.
В результате инвертор может достигать хороших динамических характеристик. Наконец, результаты моделирования и эксперимента приведены для проверки теоретического анализа.
- Публикация:
Journal of Electrical Engineering & Технология
- Дата публикации:
- Май 2022
- DOI:
10.1007/s42835-022-01097-0
- Биб-код:
2022JEET..tmp..130Z
- Ключевые слова:
- Раздельная схема управления;
- Синхронная система отсчета;
- Контроль тока;
- Трехфазный инвертор;
- Комплексный ПИ-регулятор
Помехоустойчивая схема динамической развязки импульсов для квантовой памяти
Модель квантовой памяти
Рисунок 1
(a) Двухуровневая структура типичной квантовой памяти, где два спиновых состояния \(\left| g\right\rangle\) и \(\left| s\right\rangle\) управляются последовательностью импульсов DD для увеличения времени хранения. (б) Эскиз зашумленного \(\pi\) импульса. Здесь это вращение вокруг оси x с углом \(\theta =\pi\). Из-за воздействия шумов возникают ошибки как по осям, так и по углу поворота. Сведение к минимуму этой импульсной ошибки является важной целью последовательности DD, состоящей из нескольких импульсов \(\pi\). 9{3+}:\hbox {Y}_{2}\hbox {SiO}_{5}\), как пример платформ квантовой памяти 14, 15 . В этих системах используется ансамбль ионов с двухуровневой структурой, включающей два спиновых состояния \(\left| g\right\rangle\) и \(\left| s\right\rangle\), как показано на рис. 1a. Мы используем спиновые состояния \(\left| g\right\rangle\) и \(\left| s\right\rangle\) для долговременного хранения, поскольку эти состояния имеют длительное время когерентности. Однако спиновые состояния в твердых системах, как правило, подвержены процессам декогеренции, источником которой являются различные источники, в том числе зарядовый шум, ядерные спиновые флуктуации, тепловые флуктуации и т.
(б) Эскиз зашумленного \(\pi\) импульса. Здесь это вращение вокруг оси x с углом \(\theta =\pi\). Из-за воздействия шумов возникают ошибки как по осям, так и по углу поворота. Сведение к минимуму этой импульсной ошибки является важной целью последовательности DD, состоящей из нескольких импульсов \(\pi\). 9{3+}:\hbox {Y}_{2}\hbox {SiO}_{5}\), как пример платформ квантовой памяти 14, 15 . В этих системах используется ансамбль ионов с двухуровневой структурой, включающей два спиновых состояния \(\left| g\right\rangle\) и \(\left| s\right\rangle\), как показано на рис. 1a. Мы используем спиновые состояния \(\left| g\right\rangle\) и \(\left| s\right\rangle\) для долговременного хранения, поскольку эти состояния имеют длительное время когерентности. Однако спиновые состояния в твердых системах, как правило, подвержены процессам декогеренции, источником которой являются различные источники, в том числе зарядовый шум, ядерные спиновые флуктуации, тепловые флуктуации и т. д. При этом ведущим источником шума являются флуктуации спина расщепление энергии из-за взаимодействия с соседними ядерными спинами 17 . Чтобы преодолеть эту расфазировку, мы можем применить к этим спиновым состояниям последовательности DD (т. е. серию микроволновых или радиочастотных импульсов \(\pi\)). Импульсы \(\pi\) меняют населенность между спиновыми состояниями \(\left| g\right\rangle\) и \(\left| s\right\rangle\). Во вращающейся системе отсчета управляющих импульсов модельный гамильтониан для управления спиновыми состояниями может быть выражен как 15, 16, 20
д. При этом ведущим источником шума являются флуктуации спина расщепление энергии из-за взаимодействия с соседними ядерными спинами 17 . Чтобы преодолеть эту расфазировку, мы можем применить к этим спиновым состояниям последовательности DD (т. е. серию микроволновых или радиочастотных импульсов \(\pi\)). Импульсы \(\pi\) меняют населенность между спиновыми состояниями \(\left| g\right\rangle\) и \(\left| s\right\rangle\). Во вращающейся системе отсчета управляющих импульсов модельный гамильтониан для управления спиновыми состояниями может быть выражен как 15, 16, 20
$$\begin{aligned} H_{0}(t)=\frac{ \Delta}{2}\sigma_{z}+\frac{\Omega}{2}\sigma_{x}, \end{aligned}$$
(1)
где \(\sigma _{x}\) и \(\sigma _{z}\) — операторы Паули, определенные в подпространстве \(\left| g\right\rangle\) и \(\left| s\right\rangle\), \(\Delta\) — частотная расстройка импульса (т. е. расщепление энергии между двумя уровнями), а \(\Omega\) — амплитуда возбуждения импульса (т. {2}}}\right] , \end{align}$$
{2}}}\right] , \end{align}$$
(2)
, который производит поворот на угол \(\theta\) вокруг оси \(\Delta {\hat{z}} +\Omega {\hat{x}}\), как показано на рис. 1б. Здесь для удобства мы используем индекс 0 для обозначения случая без шумов и устанавливаем постоянную Планка \(\hslash =1\). Обычно мы предполагаем, что возбуждающая амплитуда намного больше, чем расстройка частоты как \(\Omega \gg \Delta\), тогда мы можем получить импульс \(\pi\) вокруг оси \({\hat{x}} \), удерживая \(\Omega\) постоянным в течение времени \(\pi /\Omega\).
Однако это предположение или приближение недействительно в различных схемах квантовой памяти из-за необходимой нам высокой точности. Что еще более важно, система испытывает два вида шумов: с одной стороны, неоднородное спиновое уширение и окружающие шумы добавляют к гамильтониану небольшую флуктуационную составляющую \(\delta \Delta\). С другой стороны, несовершенства приводят к деформации управляющих импульсов и, в свою очередь, структуры энергетических уровней. Помимо ошибки расстройки, эти управляющие шумы также приводят к возмущению \(\delta \Omega\) относительно амплитуды. Колебания параметров системы изменяют как оси, так и угол поворота, как показано на рис. 1b. Эта ошибка значительно снижает точность импульсов \(\pi\) и, следовательно, последовательностей импульсов DD. Чтобы решить эту проблему, мы разработали составной импульс для достижения высокой точности работы, поскольку он устойчив к шуму.
Помимо ошибки расстройки, эти управляющие шумы также приводят к возмущению \(\delta \Omega\) относительно амплитуды. Колебания параметров системы изменяют как оси, так и угол поворота, как показано на рис. 1b. Эта ошибка значительно снижает точность импульсов \(\pi\) и, следовательно, последовательностей импульсов DD. Чтобы решить эту проблему, мы разработали составной импульс для достижения высокой точности работы, поскольку он устойчив к шуму.
Общая стратегия проектирования защищенного от помех вращения
Цель состоит в том, чтобы спроектировать серию составных импульсов таким образом, чтобы все составляющие ошибки компенсировались друг другом. Существует много подходов к разработке этих составных импульсов 18, 19 , в то время как мы следуем идее динамически скорректированных вентилей, чтобы наметить подробную процедуру для схемы 37, 38 .
(i) Начните с шумного оператора элементарного импульса. Гамильтониан с шумами можно записать в виде 9{2}}}\справа] . \end{aligned}$$
\end{aligned}$$
(4)
На практике можно динамически управлять системными параметрами \(\Delta\) и \(\Omega\), значения которых ограничены от нуля до определенного максимального положительного значения . Это приведет к ограничению конструкции регулируемых параметров. В приведенных ниже расчетах мы рассматриваем эти два источника шума как квазистатические, где каждый шум моделируется случайным значением из распределения Гаусса со стандартным отклонением. Эволюция времени усредняется по многим повторениям, чтобы получить окончательный результат; для каждого повторения отбираются новые значения статического шума. 9{2}}}\right] \nonumber \\&\quad \times \left( I_{0}-i\sum _{k=x,y,z}\varepsilon _{k}\sigma _{k} \right) \nonumber \\&= {} U_{0}(\Delta {\шляпа{z}}+\Omega {\шляпа{x}},\theta ) \left(I_{0}-i\sum _{k=x,y,z}\varepsilon _{k}\sigma _{k}\right) . \end{align}$$
(5)
Здесь \(U_{0}(\Delta {\hat{z}}+\Omega {\hat{x}},\theta )\) — бесшумная импульсный оператор, \(I_{0}\) — обычный тождественный оператор, \(\sigma _{k}\) — оператор Паули и \(\varepsilon _{k}\) — член ошибки из-за шума источники \(\delta \Delta\) и \(\delta \Omega\). (Мы можем рассчитать ошибки в этих операторах как функцию \(\delta \Delta\) и \(\delta \Omega\), подробности см. в дополнительной информации). 9{(n-1)} \nonumber \\&\quad \times U(\Delta _ {n}{\hat{z}}+\Omega _{n}{\hat{x}},m_{n} \pi -\theta _{n})\nonumber \\&= {} U(\Delta _{n}{\hat{z}}+\Omega _{n}{\hat{x}},m_{ n}\pi +\theta _{n}) \nonumber \\&\quad \times U(\Delta _ {n-1}{\hat{z}}+\Omega _{n-1}{\hat {x}},m_{n-1}\pi +\theta _{n-1})… \nonumber \\&\quad \times U(\Delta _{1}{\hat{z}} +\Omega _{1}{\шляпа{x}},m_{1}\pi +\theta _{1})U(\Delta _{0}{\шляпа{z}}+\Omega _{0 }{\шляпа{x}},2m_{0}\pi ) \nonumber \\&\quad \times U(\Delta _{1}{\шляпа{z}}+\Omega _{1}{\шляпа {x}},m_{1}\pi -\theta _{1})…\nonumber \\&\quad \times U(\Delta _{n-1}{\hat{z}}+\ Omega _ {n-1}{\hat{x}},m_{n-1}\pi -\theta _{n-1}) \nonumber \\&\quad \times U(\Delta _{n} {\шляпа{z}}+\Omega _{n}{\шляпа{x}},m_{n}\pi -\theta _{n}). \end{выровнено}$$
(Мы можем рассчитать ошибки в этих операторах как функцию \(\delta \Delta\) и \(\delta \Omega\), подробности см. в дополнительной информации). 9{(n-1)} \nonumber \\&\quad \times U(\Delta _ {n}{\hat{z}}+\Omega _{n}{\hat{x}},m_{n} \pi -\theta _{n})\nonumber \\&= {} U(\Delta _{n}{\hat{z}}+\Omega _{n}{\hat{x}},m_{ n}\pi +\theta _{n}) \nonumber \\&\quad \times U(\Delta _ {n-1}{\hat{z}}+\Omega _{n-1}{\hat {x}},m_{n-1}\pi +\theta _{n-1})… \nonumber \\&\quad \times U(\Delta _{1}{\hat{z}} +\Omega _{1}{\шляпа{x}},m_{1}\pi +\theta _{1})U(\Delta _{0}{\шляпа{z}}+\Omega _{0 }{\шляпа{x}},2m_{0}\pi ) \nonumber \\&\quad \times U(\Delta _{1}{\шляпа{z}}+\Omega _{1}{\шляпа {x}},m_{1}\pi -\theta _{1})…\nonumber \\&\quad \times U(\Delta _{n-1}{\hat{z}}+\ Omega _ {n-1}{\hat{x}},m_{n-1}\pi -\theta _{n-1}) \nonumber \\&\quad \times U(\Delta _{n} {\шляпа{z}}+\Omega _{n}{\шляпа{x}},m_{n}\pi -\theta _{n}). \end{выровнено}$$
(6)
Здесь n обозначает уровень рекурсивной формы, \(m_{n}\) — целое число, \(\Delta _{n}\), \(\Omega _{n} \) и \(\,\theta _{n}\) — ось вращения и угол поворота, которые необходимо определить. Заметим, что эта рекурсивная форма имеет ряд преимуществ: во-первых, она имеет интуитивно понятную физическую картину, означающую, что составной импульс состоит из серии вращений с разными осями и углами на сфере Блоха. Во-вторых, он предлагает бесплатные параметры \(\Delta _{n}\), \(\Omega _{n}\) и \(\theta _{n}\) для каждого импульса, чтобы обеспечить шумоподавление всего импульса. последовательность. 9{(n)}\sigma _{k}, \end{aligned}$$
Заметим, что эта рекурсивная форма имеет ряд преимуществ: во-первых, она имеет интуитивно понятную физическую картину, означающую, что составной импульс состоит из серии вращений с разными осями и углами на сфере Блоха. Во-вторых, он предлагает бесплатные параметры \(\Delta _{n}\), \(\Omega _{n}\) и \(\theta _{n}\) для каждого импульса, чтобы обеспечить шумоподавление всего импульса. последовательность. 9{(n)}\sigma _{k}, \end{aligned}$$
(7)
, где \(I_{0}\) — стандартный тождественный оператор, \(\Theta _{k}\ ) — это член ошибки, возникающий из-за накопления членов шума \(\delta \Delta\) и \(\delta \Omega\). В расчетах мы можем выполнить матричное умножение, чтобы получить \(\Theta _{k}\) как функцию параметров импульса \(\Delta _{n}\), \(\Omega _{n}\) и \(\тета _{n}\).
(v) Настройте свободные параметры так, чтобы сумма всех составляющих ошибки каждого импульса равнялась нулю. Для целевой операции \(U(\Delta _{t} {\hat{z}}+\Omega _{t}{\hat{x}},\theta _{t})\) мы используем всю составной импульс как \(U_{c}={\tilde{I}}^{(n)}U(\Delta _{t}{\hat{z}}+\Omega _{t}{\hat{x }},\theta _{t})\) и получим выражение 9{(n)}\), мы можем выбрать параметры для выполнения уравнения
$$\begin{aligned} \varepsilon _{k}+\Theta _{k}=0. \end{aligned}$$
\end{aligned}$$
(9)
Следовательно, весь импульс \(U_{c}\) достигает целевой операции \(U_{0}(\Delta _{t}{\hat{z}} +\Omega _{t}{\hat{x}},\theta _{t})\), который также невосприимчив к ведущему порядку шумов.
Два репрезентативных случая помехоустойчивого импульса \(\pi }\)
Далее мы применяем описанную выше общую процедуру для явного построения помехоустойчивого импульса \(\pi\) около 9Ось 0068 x (т.е. целевая операция \(U(\Delta _{t}{\hat{z}}+\Omega _{t}{\hat{x}},\theta _{t}) \) где \(\Delta _{t}=0\), \(\Omega _{t}=1\), \(\theta _{t}=\pi\)). Здесь мы обсудим два репрезентативных случая, которые охватывают множество реальных ситуаций. В первом случае мы устанавливаем амплитуду возбуждения \(\Omega =1\) постоянной и расстройку частоты \(\Delta\) в качестве настраиваемого параметра.
Начнем с элементарного оператора и построим пятиуровневую последовательность импульсов для тождественного оператора 9{(5)}&= {} U(\Delta _{t}{\шляпа{z}}+{\шляпа{x}},\pi +\frac{\theta _{t}}{2} ) U(\Delta _{4}{\шляпа{z}}+{\шляпа{x}},\pi)U(\Delta_{3}{\шляпа{z}}+{\шляпа{x}} ,\pi ) \nonumber \\&\quad \times U(\Delta _ {2}{\шляпа{z}} + {\шляпа{x}},\pi )U(\Delta _{1}{\ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {0} {\ шляпа {z}} + {\ шляпа {x}}, 4 \ pi ) \ nonumber \\& \quad \times U(\Delta _{1}{\шляпа{z}}+{\шляпа{x}},\pi)U(\Delta_{2}{\шляпа{z}}+{\шляпа {x}},\pi )U(\Delta _{3}{\шляпа{z}}+{\шляпа{x}},\pi ) \nonumber \\&\quad \times U(\Delta _{ 4}{\шляпа{z}}+{\шляпа{x}},\pi )U\left(\Delta _{t}{\шляпа{z}}+{\шляпа{x}},\pi — \ гидроразрыва {\ тета _ {т}} {2} \ справа) . \end{выровнено}$$
\end{выровнено}$$
(10)
Здесь мы выбираем параметры угла как \(m_{0}=2\), \(m_{1,2,3,4,5}=1\), \(\theta _{ 1,2,3,4}=0\), \(\theta _{5}=\frac{\theta _{t}}{2}\) и один параметр расстройки как \(\Delta _{5} =\Delta _{t}\), и используйте другие величины расстройки \(\Delta _{0,1,2,3,4}\) в качестве свободных параметров.
Заметим, что из-за нелинейности уравнений свободных параметров не гарантируется вещественность и неотрицательность решений, как это требуется. Например, если выбрать 2-х или 3-х уровневую импульсную последовательность, численное решение этих уравнений всегда дает нефизическое решение параметров. На самом деле, более длинная последовательность, такая как 5-уровневая последовательность импульсов, обеспечивает достаточную свободу, так что шумоподавление всегда возможно для всех изученных нами случаев, что явно продемонстрировано в настоящей работе. Таким образом, выбор длины последовательности импульсов является компромиссом между более длинным импульсом для гибкости и более коротким импульсом для удобства. 9{(5)}U(\Delta_{t}{\шляпа{z}}+{\шляпа{x}},\theta_{t}) \nonumber \\&= {} U\left(\Delta _ {t} {\ hat {z}} + {\ hat {x}}, \ pi + \ frac {\ theta _ {t}} {2} \ right) U (\ Delta _ {4} \ hat { z} + {\ hat {x}}, \ pi ) U (\ Delta _ {3} {\ hat {z}} + {\ hat {x}}, \ pi ) \ nonumber \\ & \ quad \ times U (\ Delta _ {2} {\ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {1} {\ шляпа {z}} + {\ шляпа {x}} ,\pi )U(\Delta _{0}{\шляпа{z}}+{\шляпа{x}},4\pi ) \nonumber \\&\quad \times U(\Delta _{1}{ \ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {2} {\ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {3}{\шляпа{z}}+{\шляпа{x}},\pi ) \не число \\&\quad \times U(\Delta _ {4}{\шляпа{z}}+{\шляпа {x}},\pi )U\left(\Delta _{t}{\шляпа{z}}+{\шляпа{x}},\pi + \frac{\theta _{t}}{2} \right) , \end{align}$$
9{(5)}U(\Delta_{t}{\шляпа{z}}+{\шляпа{x}},\theta_{t}) \nonumber \\&= {} U\left(\Delta _ {t} {\ hat {z}} + {\ hat {x}}, \ pi + \ frac {\ theta _ {t}} {2} \ right) U (\ Delta _ {4} \ hat { z} + {\ hat {x}}, \ pi ) U (\ Delta _ {3} {\ hat {z}} + {\ hat {x}}, \ pi ) \ nonumber \\ & \ quad \ times U (\ Delta _ {2} {\ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {1} {\ шляпа {z}} + {\ шляпа {x}} ,\pi )U(\Delta _{0}{\шляпа{z}}+{\шляпа{x}},4\pi ) \nonumber \\&\quad \times U(\Delta _{1}{ \ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {2} {\ шляпа {z}} + {\ шляпа {x}}, \ pi ) U (\ Delta _ {3}{\шляпа{z}}+{\шляпа{x}},\pi ) \не число \\&\quad \times U(\Delta _ {4}{\шляпа{z}}+{\шляпа {x}},\pi )U\left(\Delta _{t}{\шляпа{z}}+{\шляпа{x}},\pi + \frac{\theta _{t}}{2} \right) , \end{align}$$
(11)
, где нижний индекс для ясности обозначает весь импульс как CP1. Отметим, что весь составной импульс представляет собой симметричную последовательность импульсов. Требование шумоподавления \(\varepsilon _{k}+\Theta _{k}=0\) приводит к набору нелинейных связанных уравнений для свободных параметров \(\Delta _{0,1,2,3,4 }\). Путем численного решения этих уравнений мы получаем требуемые расстройки частот и показываем результаты в таблице 1 (здесь мы установили \(\Omega =1\) в качестве базовой единицы энергии).
Путем численного решения этих уравнений мы получаем требуемые расстройки частот и показываем результаты в таблице 1 (здесь мы установили \(\Omega =1\) в качестве базовой единицы энергии).
Таблица 1 Параметры разработанного составного импульса в уравнении. (11).
Полноразмерная таблица
Таблица 2 Параметры расчетного составного импульса в уравнении. (14).
Полноразмерная таблица
Теперь рассмотрим второй случай, когда мы установили расстройку частоты \(\Delta =1\) как постоянную, а амплитуду возбуждения \(\Omega\) как регулируемый параметр. Поскольку расстройка \(\Delta\) имеет ненулевое значение, мы не можем напрямую добиться поворота вокруг оси x независимо от любого значения \(\Omega\). В качестве альтернативы мы используем трехступенчатый импульс для реализации x -вращение оси как
$$\begin{aligned} U(\Omega _{t}{\hat{x}},\theta _{t})=U(\Delta _{t}{\ шляпа{z}}+\Omega _{t}{\шляпа{x}} ,\pi )U(\Delta _{t}{\шляпа{z}},\theta _{t})U(\Delta _{t}{\hat{z}}+\Omega _{t}{\hat{x}},\pi ), \end{aligned}$$
(12)
(т. е. целевая операция равно \(U(\Omega _{t}{\hat{x}},\theta _{t})\), где \(\Delta _{t}=1\), \(\Omega _{t} =1\), \(\тета _{t}=\pi\)).
е. целевая операция равно \(U(\Omega _{t}{\hat{x}},\theta _{t})\), где \(\Delta _{t}=1\), \(\Omega _{t} =1\), \(\тета _{t}=\pi\)).
Рисунок 2
(a) Часто используемый прямоугольный импульс \(\pi\). Установка \(\Delta =0\) и \(\Omega =1\) на длительность \(\pi\) приводит к типичному \(\pi\) импульсу. 9{(5)}&= {} U\left( {\шляпа{z}},\pi +\frac{\theta _{t}}{2}\right) U({\шляпа{z}}+ \ Omega _ {4} {\ hat {x}}, \ pi ) U ({\ hat {z}} + \ Omega _ {3} {\ hat {x}}, \ pi ) \ nonumber \\&\ quad \times U({\шляпа{z}}+\Omega _{2}{\шляпа{x}},\pi)U({\шляпа{z}}+\Omega _{1}{\шляпа{ x}}, \ pi ) U ({\ hat {z}} + \ Omega _ {0} {\ hat {x}}, 2 \ pi ) \ nonumber \\ & \ quad \ times U ({\ hat { z}}+\Omega _{1}{\шляпа{x}},\pi)U({\шляпа{z}}+\Omega _{2}{\шляпа{x}},\pi)U( {\шляпа{z}}+\Omega _{3}{\шляпа{x}},\pi ) \nonumber \\&\quad \times U({\шляпа{z}}+\Omega _{4} {\шляпа{x}},\pi)U\влево({\шляпа{z}},\pi -\frac{\theta _{t}}{2}\right) . \end{выровнено}$$
(13)
Здесь мы фиксируем параметры угла как \(m_{0,1,2,3,4,5}=1\), \(\theta _{1,2,3,4}= 0\), \(\theta _{5}=\frac{\theta _{t}}{2}\) и один параметр амплитуды как \(\Omega _{5}=0\), и использовать другую амплитуду количества \(\Omega _{0,1,2,3,4}\) в качестве свободных параметров.
Наконец, мы вставляем тождественный оператор между \(U({\шляпа{z}}+{\шляпа{х}},\pi )\) и \(U({\шляпа{z}},\theta _ {t})\) в уравнении (12), и мы получаем симметричный составной импульс как
$$\begin{aligned} U_{cp2}&= {} U({\hat{z}}+{\hat{x}},\pi ) U \ влево ( {\ шляпа {z}}, \ pi + \ frac {\ theta _ {t}} {2} \ справа) U ( {\ шляпа {z}} + \ Omega _ {4} {\ шляпа {x}}, \ pi ) U ({\ hat {z}} + \ Omega _ {3} {\ hat {x}}, \ pi ) \ nonumber \\ & \ quad \ times U ({\ hat { z}}+\Omega _{2}{\шляпа{x}},\pi)U({\шляпа{z}}+\Omega _{1}{\шляпа{x}},\pi)U( {\шляпа{z}}+\Omega _{0}{\шляпа{x}},2\pi ) \nonumber \\&\quad \times U({\шляпа{z}}+\Omega _{1 }{\шляпа{х}},\пи)U({\шляпа{z}}+\Omega _{2}{\шляпа{х}},\пи)U({\шляпа{z}}+\ Omega _ {3}{\шляпа{x}},\pi ) \nonumber \\&\quad \times U({\шляпа{z}}+\Omega _{4}{\шляпа{x}},\ пи ) U \ влево ( {\ шляпа {z}}, \ пи + \ гидроразрыва {\ theta _ {t}} {2} \ справа) U ({\ шляпа {z}} + {\ шляпа {х}} ,\pi ), \end{выровнено}$$
(14)
, где мы обозначаем весь импульс как CP2. Требование нечувствительности к шуму дает набор связанных уравнений для переменных \(\Omega _{0,1,2,3,4}\). Мы определили результаты для этих регулируемых параметров, которые представлены в таблице 2. CP1 при установке \(\Omega =1\) и CP2 при установке \(\Delta =1\) соответственно) и обычно используемый прямоугольный импульс \(\pi\) (обозначается как RF). (a) Неверность как функция флуктуации расстройки частоты \(\delta \Delta /\Delta\). Симуляция находится под шумом \(\delta \Omega /\Omega =0.01\). (б) Неверность как функция колебания амплитуды возбуждения \(\дельта \Омега /\Омега\). Эволюция проходит под шумом \(\delta \Delta /\Delta =0.01\).
Требование нечувствительности к шуму дает набор связанных уравнений для переменных \(\Omega _{0,1,2,3,4}\). Мы определили результаты для этих регулируемых параметров, которые представлены в таблице 2. CP1 при установке \(\Omega =1\) и CP2 при установке \(\Delta =1\) соответственно) и обычно используемый прямоугольный импульс \(\pi\) (обозначается как RF). (a) Неверность как функция флуктуации расстройки частоты \(\delta \Delta /\Delta\). Симуляция находится под шумом \(\delta \Omega /\Omega =0.01\). (б) Неверность как функция колебания амплитуды возбуждения \(\дельта \Омега /\Омега\). Эволюция проходит под шумом \(\delta \Delta /\Delta =0.01\).
Полноразмерное изображение
Используя параметры в таблицах, мы разрабатываем защищенные от помех \(\pi\) импульсы, как показано на рис. 2. Для сравнения, рис. 2a представляет собой обычно используемый прямоугольный импульс, а рис. 2b,c представляют собой составные импульсы, основанные на рассчитанных расстройках частоты и возбуждающих амплитудах соответственно. Отметим, что прямоугольный импульс является физически идеальным случаем с приближением \(\Omega \gg \Delta\). Чтобы сравнить производительность различных импульсов, мы вычисляем точность импульсов при реалистичных шумах. Отметим, что типичный диапазон значений отношения шума к управляющему полю (\(\frac{ \delta \Omega }{\Omega }\) или \(\frac{\delta \Delta}{\Delta } \)) в твердотельной спиновой системе находится в пределах от 0 до 0,1 17, 33, 39 . Верность определяется формулой 40
Отметим, что прямоугольный импульс является физически идеальным случаем с приближением \(\Omega \gg \Delta\). Чтобы сравнить производительность различных импульсов, мы вычисляем точность импульсов при реалистичных шумах. Отметим, что типичный диапазон значений отношения шума к управляющему полю (\(\frac{ \delta \Omega }{\Omega }\) или \(\frac{\delta \Delta}{\Delta } \)) в твердотельной спиновой системе находится в пределах от 0 до 0,1 17, 33, 39 . Верность определяется формулой 40
$$\begin{aligned} F=\text {Tr(}\sqrt{\sqrt{\rho _{0}}\rho \sqrt{\rho _{0 }}}\text {)}, \end{aligned}$$
(15)
где \(\rho _{0}\) — матрица плотности системы без шумов и \(\rho\ ) — матрица плотности под шумами. На рис. 3 показана погрешность \(1-F\) для трех импульсов \(\pi\) при различных типах шумов. На рис. 3 мы видим, что помехоустойчивые импульсы обеспечивают компенсацию ошибок, а погрешность на несколько порядков меньше, чем у обычного импульса \(\pi\). На рис. 3а мы сохраняем амплитудный шум \(\frac{ \delta \Omega }{\Omega }=0,01\) и исследуем влияние флуктуации частоты \(\delta \Delta\). Импульс CP1 \(\pi\) работает лучше всего и достигает погрешности ниже, чем \(0,01\%\), даже при наличии большого шума \(\frac{\delta \Delta}{\Delta}=0,1\ ). Импульс CP2 \(\pi\) достигает второй небольшой погрешности, а обычно используемый прямоугольный импульс \(\pi\) получает наибольшую погрешность. На рис. 3б мы рассматриваем основной шум, который исходит от флуктуации амплитуды \(\delta \Omega\). Импульс CP2 \(\pi\) работает лучше всего с погрешностью ниже \(0,001\%\) даже при большом шуме \(\frac{\delta\Omega}{\Omega}=0,1\). Как и ожидалось, импульс CP1 \(\pi\) занимает второе место, а обычный импульс \(\pi\) — последний.
3а мы сохраняем амплитудный шум \(\frac{ \delta \Omega }{\Omega }=0,01\) и исследуем влияние флуктуации частоты \(\delta \Delta\). Импульс CP1 \(\pi\) работает лучше всего и достигает погрешности ниже, чем \(0,01\%\), даже при наличии большого шума \(\frac{\delta \Delta}{\Delta}=0,1\ ). Импульс CP2 \(\pi\) достигает второй небольшой погрешности, а обычно используемый прямоугольный импульс \(\pi\) получает наибольшую погрешность. На рис. 3б мы рассматриваем основной шум, который исходит от флуктуации амплитуды \(\delta \Omega\). Импульс CP2 \(\pi\) работает лучше всего с погрешностью ниже \(0,001\%\) даже при большом шуме \(\frac{\delta\Omega}{\Omega}=0,1\). Как и ожидалось, импульс CP1 \(\pi\) занимает второе место, а обычный импульс \(\pi\) — последний.
Применение последовательностей импульсов DD
Последовательность импульсов DD состоит из двух основных процессов 16 . Одним из них является импульс \(\pi\) вокруг оси x (или другой оси), который описывается оператором \(U({\hat{x}},\pi )\). Другой — это свободная эволюция системы, которая задается оператором
Другой — это свободная эволюция системы, которая задается оператором
$$\begin{aligned} V({\hat{z}},\tau )=\exp \left[ -i\left( \ frac{\Delta}{2}\sigma _{z}\right) \tau \right] . \end{выровнено}$$
(16)
Здесь \(\tau\) — интервал времени между соседними \(\pi\) импульсами. Строительный блок последовательности DD записывается как
$$\begin{aligned} U_{{\hat{x}}}=V({\hat{z}},\tau)U({\hat{x }},\pi )V({\hat{z}},\tau ), \end{aligned}$$
(17)
, где нижний индекс обозначает импульс \(\pi\) около x оси для ясности. Механизм схемы ДД интуитивно понятен: поскольку ошибка в члене расстройки \(\Delta \tau\) имеет разные знаки до и после импульса \(\pi\), эффект неоднородного уширения или флуктуаций расстройки усредняется. Таким образом, последовательность импульсов DD может быть построена путем повторения основных элементов.
Существуют виды последовательностей импульсов DD, которые формируются из нескольких \(\pi\) импульсов в периодических или непериодических структурах 16 . Здесь мы сосредоточимся на трех примерах последовательностей DD, которые широко применяются в области квантовой памяти. Первый тип протокола DD представляет собой последовательность Carl-Purcell-Meiboom-Gilles (CPMG) 41, 42 . Последовательность CPMG состоит из двух импульсов \(\pi\) вокруг оси x , что является простейшим расширением обычного спинового эха. Последовательность импульсов CPMG можно описать как
Здесь мы сосредоточимся на трех примерах последовательностей DD, которые широко применяются в области квантовой памяти. Первый тип протокола DD представляет собой последовательность Carl-Purcell-Meiboom-Gilles (CPMG) 41, 42 . Последовательность CPMG состоит из двух импульсов \(\pi\) вокруг оси x , что является простейшим расширением обычного спинового эха. Последовательность импульсов CPMG можно описать как
$$\begin{align} U_{CPMG}&= {} U_{{\hat{x}}}U_{{\hat{x}}} \nonumber \\&= {} V({\hat {z}},\tau)U({\шляпа{x}},\pi)V({\шляпа{z}},\tau)V({\шляпа{z}},\tau)U({ \шляпа{х}},\пи)V({\шляпа{z}},\тау). \end{aligned}$$
(18)
Второй тип — это так называемая последовательность XY4 43 , которая состоит из четырех \(\pi\) импульсов с чередованием оси вращения вокруг x и и направлений. Последовательность XY4 введена для частичной компенсации ошибок амплитуды для любого начального состояния. Кроме того, последовательность XY4 в некоторой степени более устойчива к ошибкам в импульсах 44 . Его можно записать как повторение строительных блоков:
Его можно записать как повторение строительных блоков:
$$\begin{aligned} U_{XY4}&= {} U_{{\hat{y}}}U_{{\hat{x}}}U_ {{\ hat {y}}} U_ {{\ hat {x}}} \ nonumber \\ & = {} V ({\ hat {z}}, \ tau ) U ({\ hat {y}}, \pi)V({\шляпа{z}},\tau)V({\шляпа{z}},\tau)U({\шляпа{x}},\pi)V({\шляпа{z} },\tau) \nonumber \\&\quad \times V({\шляпа{z}},\tau)U({\шляпа{y}},\pi)V({\шляпа{z}}, \ тау ) V ({\ шляпа {z}}, \ тау ) U ( {\ шляпа {х}}, \ пи ) V ({\ шляпа {z}}, \ тау ). \end{aligned}$$
(19)
Третий тип — последовательность UDD 9{2}[j\pi /(2N+2)]\), где \(\tau _{D}\) — общая длительность последовательности импульсов.
В приложениях DD для квантовой памяти, чтобы увеличить время хранения, можно повторять последовательности несколько раз, например \(U_{{\hat{x}}}U_{{\hat{x}} }.. .U_{{\шляпа{х}}}U_{{\шляпа{х}}}\). Итоговые последовательности DD состоят из N последовательных поворотов на номинальный угол \(\pi\) вокруг определенной оси, где N обозначает количество \(\pi\) импульсов или длину последовательности. В идеальных условиях оператор эволюции всей последовательности DD соответствует операции тождества. Однако в реальных ситуациях мы должны учитывать кумулятивный эффект несовершенства импульса. Если фактическое вращение каждого импульса отличается на флуктуации \(\delta \Delta\) и \(\delta \Omega\), ошибка накапливается в течение N импульсов, и общий пропагатор последовательности DD становится равным
В идеальных условиях оператор эволюции всей последовательности DD соответствует операции тождества. Однако в реальных ситуациях мы должны учитывать кумулятивный эффект несовершенства импульса. Если фактическое вращение каждого импульса отличается на флуктуации \(\delta \Delta\) и \(\delta \Omega\), ошибка накапливается в течение N импульсов, и общий пропагатор последовательности DD становится равным
$$\begin{aligned} U_{dd}=I_{0}+i\sum _{k=x,y,z}D_{k}\ sigma _{k}, \end{aligned}$$
(20)
, где \(D_{k}\) обозначает ошибку из-за шумов в каждом импульсе.
Рисунок 4
Точность F в зависимости от числа импульсов \(\pi\) в последовательности DD. Нижний индекс 1 и сплошная линия обозначают последовательность DD, построенную с помощью помехоустойчивого импульса \(\pi\), а нижний индекс 2 и пунктирная линия обозначают последовательность с использованием импульса прямоугольной формы \(\pi\). Шумы в моделировании установлены как \(\frac{\delta \Delta}{\Delta}=\frac{\delta\Omega}{\Omega}=0,01\).
Увеличенное изображение
Для компенсации ошибок из-за шумов в расстройке и амплитудах, мы комбинируем помехоустойчивые импульсы с последовательностями DD. Мы можем использовать разработанный выше помехоустойчивый импульс \(\pi\) для замены шумного импульса \(\pi\) в последовательностях DD. Для сравнения мы также рассматриваем последовательность DD с использованием обычного импульса прямоугольной формы \(\pi\). Чтобы проиллюстрировать улучшение, мы исследуем точность различных последовательностей импульсов DD. Во многих случаях мы хотим количественно оценить согласие не между состояниями, а между двумя эволюциями. Соответствующая точность процесса может быть определена по аналогии с точностью состояния 9{\dagger}U_{B}}}} \end{aligned}$$
(21)
где \(U_{A}\) — целевой пропагатор, такой как единица в идеальной ситуации, и \ (U_{B}\) — фактический пропагатор, реализуемый импульсами DD.
На рис. 4 показаны смоделированные характеристики последовательностей DD в зависимости от длины последовательности импульсов. Фактический пропагатор, генерируемый обычным прямоугольным импульсом \(\pi\), имеет исчезающее перекрытие с целевым пропагатором, а точность операции равна нулю для долговременной последовательности. Напротив, мы обнаружили, что точность комбинированной последовательности DD значительно выше даже для последовательности большой продолжительности, в частности, для случая UDD. Эти результаты показывают, что последовательности DD более надежны и эффективны при использовании помехоустойчивых импульсов \(\pi\). Поскольку обычные последовательности DD были выполнены для продления срока службы квантовой памяти 17, 45 , можно ожидать, что предложенный здесь усовершенствованный метод DD может значительно увеличить время жизни квантовой памяти при увеличении числа импульсов DD.
Фактический пропагатор, генерируемый обычным прямоугольным импульсом \(\pi\), имеет исчезающее перекрытие с целевым пропагатором, а точность операции равна нулю для долговременной последовательности. Напротив, мы обнаружили, что точность комбинированной последовательности DD значительно выше даже для последовательности большой продолжительности, в частности, для случая UDD. Эти результаты показывают, что последовательности DD более надежны и эффективны при использовании помехоустойчивых импульсов \(\pi\). Поскольку обычные последовательности DD были выполнены для продления срока службы квантовой памяти 17, 45 , можно ожидать, что предложенный здесь усовершенствованный метод DD может значительно увеличить время жизни квантовой памяти при увеличении числа импульсов DD.
На рис. 4 показано, что вставка защищенного от шума импульса в последовательность XY4 мало что дает. Мы подозреваем, что есть две возможные причины. Одна из причин заключается в том, что последовательность XY4 определяется как чередование импульсов в направлении x и y , поэтому эффект вращения вокруг двух осей компенсирует друг друга.

 Предпортовая
Предпортовая
 Выполнен в удобном формате
Выполнен в удобном формате