ГлавнаяРазноеОпределить тип дифференциального уравнения

Как определять тип дифференциального уравнения первого порядка. Определить тип дифференциального уравнения


Определение типа дифференциального уравнения первого порядка

Для выбора пути решения заданного дифференциального уравнения первого порядка сначала надо определить тип, к которому оно относится. Для этого следует разрешить данное уравнение относительно производной, то есть привести его к виду 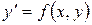. После этого надо посмотреть, не разлагается ли функция 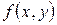на множители, один из которых зависит только от 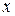, а второй – только от 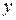. Если это возможно, то надо разделить переменные и интегрировать обе части получившегося равенства.

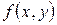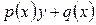Если переменные не разделяются непосредственно, то следует проверить, является ли данное уравнение линейным или уравнением Бернулли, то есть имеет ли функция вид или .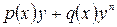

К уравнению Бернулли также сводятся уравнения вида 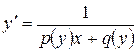(и более общего вида 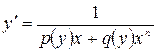). Для их решения надо поменять местами переменные 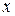и 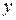и считать 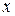функцией от 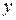. В результате для этой функции получим линейное уравнение: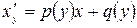

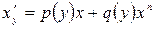(или уравнение Бернулли ). Например, уравнение 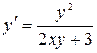, если 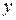считать аргументом, а 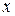– функцией, принимает вид 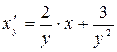, то есть становится линейным.

Если и этот метод не приводит к цели, следует проверить, не является ли 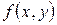однородной функцией нулевой степени. Наконец, если и этот метод окажется неудачным, надо записать заданное уравнение в виде 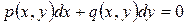и проверить, не является ли оно уравнением в полных дифференциалах.

 

Уравнения высших порядков

1.Дифференциальное уравнение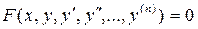

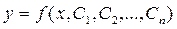называется уравнением п-го порядка. Его общее решение содержит п произвольных постоянных: , а решение задачи Коши требует задания при х = х0 значений функции у и ее производных до (п – 1)-го порядка включительно: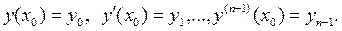

2.Если в дифференциальное уравнение не входит явным образом искомая функция у, то есть уравнение имеет вид

,

то можно понизить его порядок на k единиц, сделав замену: 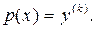Тогда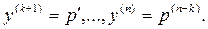

Типовой пример

Найти общее решение уравнения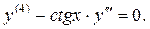

►Пусть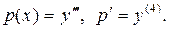

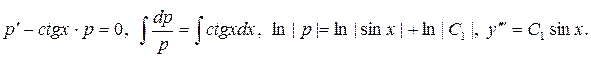Тогда Теперь трижды проинтегрируем полученное равенство по х: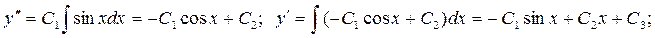

◄

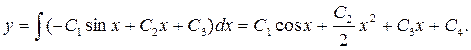3. Если дифференциальное уравнение не содержит явно независимую переменную х: 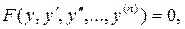то можно понизить его порядок на единицу, считая, что 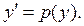Тогда 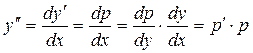, то есть вторая производная у выражается через первую производную р и т.д.

Типовой пример

Решить задачу Коши для уравнения 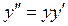, если у(1)=2, у’(1)=2.

►Замена приводит к уравнению

откуда:

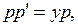
а) р = 0, у’ = 0, у = С, но у’ (1)=2 ≠ 0, значит, в этом случае решения нет;

б)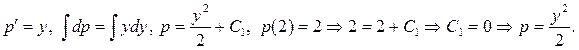

Тогда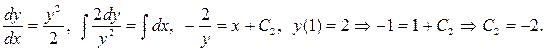

Следовательно, искомое частное решение имеет вид

◄

 

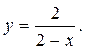Линейные дифференциальные уравнения и системы

Уравнение вида

,

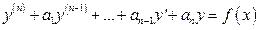где и непрерывные на промежутке 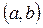функции аргумента 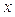, называется линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка.

ТЕОРЕМА

Если на отрезке 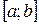коэффициенты 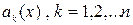и правая часть 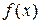уравнения непрерывны, то на всем этом отрезке существует, и притом единственное, решение дифференциального уравнения с начальными условиями 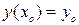, , 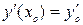… , , 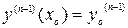где .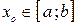

Если в данном уравнении 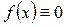, то уравнение называется линейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка. Обозначим 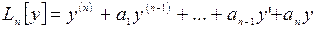левую часть линейного дифференциального уравнения и назовем линейным дифференциальным оператором n-го порядка.

Свойства линейного дифференциального оператора

. .

. .

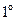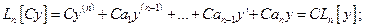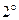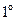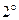Следствие. Из свойств и следует линейность оператора 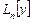, то есть

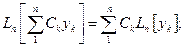
Система из 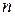линейно независимых (ЛНЗ) на промежутке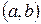

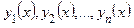решений для ЛОДУ n-го порядка называется фундаментальной системой решений (ФСР) этого уравнения.

ТЕОРЕМА

Пусть функции 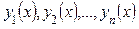являются решениями ЛОДУ n-го порядка 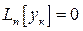с непрерывными коэффициентами. Тогда для того, чтобы система 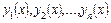была линейно независима на 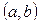, необходимо и достаточно, чтобы определитель Вронского

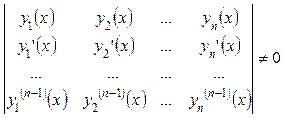
для любого .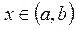

Типовой пример

Исследовать на линейную зависимость систему функций .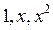

►Составим определитель Вронского:

.

Следовательно, система функций 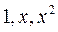– линейно независима.◄

Типовой пример

Исследовать на линейную зависимость следующую систему функций

.

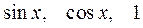►Составим определитель Вронского:

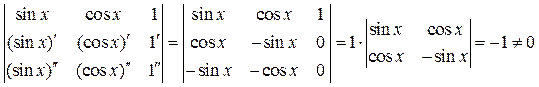
Следовательно, система функций 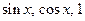- линейно независима.◄

Типовой пример

Исследовать на линейную зависимость систему функций .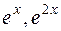

►Аналогично, 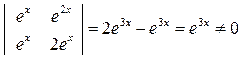для любого .

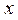Следовательно, система функций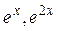

– линейно независима.◄

Таким образом, определитель Вронского играет определяющую роль в выяснении линейной зависимости системы функций.

Если определитель Вронского построен на частных решениях 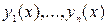дифференциального уравнения, то справедлива формула Лиувилля – Остроградского

,

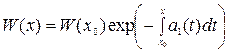где 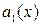– первый коэффициент дифференциального уравнения.

Для линейного однородного дифференциального уравнения второго порядка 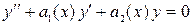фундаментальная система состоит из двух линейно независимых решений 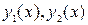; его общее решение находится по формуле .

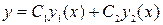Если для такого уравнения известно одно частное решение

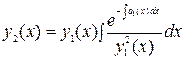, то второе его решение, линейно независимое с первым, можно найти по формуле, являющейся следствием формулы Лиувилля – Остроградского:

.

Типовой пример

Найти общее решение дифференциального уравнения 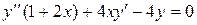, проверив, что одно его частное решение имеет вид .

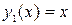►Разделим обе части данного уравнения на :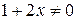

.

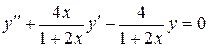Здесь коэффициенты 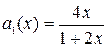и 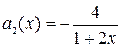непрерывны при 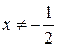, следовательно, решение дифференциального уравнения существует в области 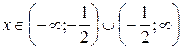. Подставляя 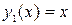, получим тождество, поэтому 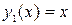является решением этого уравнения. Найдем второе частное решение по формуле. Сначала вычислим

.

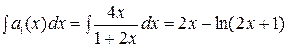Произвольную постоянную 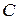при вычислении неопределенного интеграла можно не писать, так как нас интересует лишь одно частное решение.

Теперь найдем

.

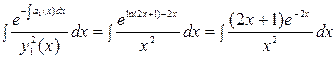Заметим, что подынтегральное выражение в последнем интеграле является производной от функции 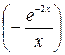, поэтому

.

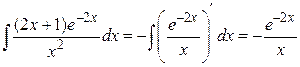(Постоянную 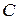здесь также можно не писать.)

Таким образом, второе частное решение исходного уравнения имеет вид

.

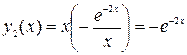Проверим, что два полученных решения линейно независимы. Вычислим определитель Вронского:

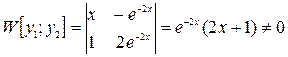при .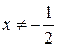

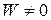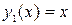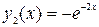В рассматриваемой области , откуда следует, что решения и линейно независимы. Тогда общее решение дифференциального уравнения будет иметь вид

,

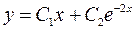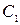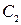где и - произвольные постоянные.◄

Читайте также:

lektsia.com

Как определять тип дифференциального уравнения первого порядка — КиберПедия

Ø Прежде всего, нужно знать типы всех уравнений и признаки каждого из них на память.

Ø Затем усвоить алгоритм распознавания типа дифференциального уравнения, который состоит из проверки признаков типов дифференциальных уравнений.

Ниже приводится сводная таблица типов дифференциальных уравнений первого порядка и их признаков.

Как только данное уравнение совпадает по признакам (или общему виду) с одним из типов, его следует решать, воспользовавшись соответствующим этому типу методом.

Чтобы определить дифференциального уравнения, его лучше записать либо в виде

, либо − как проще.

Дифференциальные уравнения второго порядка

Дифференциальное уравнение второго порядка имеет вид

(2.1)

или

. (2.2)

Общим решением уравнения (2.1) называется функция

(2.3)

Эта функция зависит от переменной x и двух произвольных постоянных , обращает данное уравнение в верное равенство.

Общее решение уравнения (2.1), заданное в неявном виде

, (2.4)

называется общим интегралом.

Частное решение

, (2.5)

где − фиксированные числа, получаются из общего решения (2.3) при фиксированных значениях .

Задача Коши. Найти решение дифференциального уравнения (2.1), удовлетворяющее условиям: .

Константы определяются из системы уравнений:

(2.6)

Дифференциальные уравнения второго порядка, допускающие

Понижение порядка

Рассмотрим три частных случая, когда решение уравнения (2.2) с помощью замены переменной сводится к решению уравнения первого порядка. Такие преобразования уравнения (2.2) называются понижением порядка.

Уравнения вида

Уравнение не содержит .

Уравнение интегрируется подстановкой , которая дает возможность свести его к уравнению с разделяющимися переменными .

Уравнения вида

Уравнение не содержитy.

Положим, как и в предыдущем случае, , тогда , и уравнение преобразуется в уравнение первого порядка относительно .

Уравнения вида

Уравнение не содержитx.

Вводим новую функцию , полагая . Тогда

.

Подставляя в уравнение выражения , получаем уравнение первого порядка относительно z как функции : .

Ниже приводится сводная таблица трех типов дифференциальных уравнений второго порядка, допускающих понижение порядка, и их признаков.

 

cyberpedia.su

37. Основные понятия и определения дифференциальных уравнений

В общем случае дифференциальное уравнение второго порядка можно записать в виде

где F− заданная функция указанных аргументов.  Если дифференциальное уравнение можно разрешить относительно второй производнойy'', то его можно представить в следующем явном виде:

В частных случаях функция fв правой части может содержать лишь одну или две переменных. Такиенеполные уравнениявключают в себя 5 различных типов:

С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка.  В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):

Итак, рассмотрим указанные случаи понижения порядка более подробно.

Случай 1. Уравнение вида  y''= f (x)

Если дано уравнение y'' = f(x), то его порядок можно понизить введением новой функцииp(x), такой, чтоy' = p(x). В результате мы получим дифференциальное уравнение первого порядка

Решая его, находим функцию p(x). Затем решаем второе уравнение

и получаем общее решение исходного уравнения.

Случай 2. Уравнение вида  y''= f (y)

Здесь правая часть уравнения зависит только от переменной y. Вводим новую функциюp(y), полагаяy' = p(y). Тогда можно записать:

и уравнение принимает вид:

Решая его, находим функцию p(y). Затем находим решение уравненияy' = p(y), то есть функциюy(x).

Случай 3. Уравнение вида  y''= f (y' )

В данном случае для понижения порядка вводим функцию y' = p(x) и получаем уравнение

которое является уравнением первого порядка с разделяющимися переменными pиx. Интегрируя, находим функциюp(x) и затем функциюy(x).

Случай 4. Уравнение вида  y''= f (x,y' )

Используем подстановку y' = p(x), гдеp(x) − новая неизвестная функция, и получаем уравнение первого порядка

Интегрируя, определяем функцию p(x). Далее решаем еще одно уравнение 1-го порядка

и находим общее решение y(x).

Случай 5. Уравнение вида  y''= f (y,y' )

Для решения такого уравнения, также как и в случае 2, вводим новую функцию p(y), полагаяy' = p(y). Дифференцирование этого равенства поxприводит к уравнению

В результате наше исходное уравнение записывается в виде уравнения 1-го порядка

Решая его, находим функцию p(y). Затем решаем еще одно уравнение первого порядка

и определяем общее решение y(x).  Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.

Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''

Если левая часть дифференциального уравнения

удовлетворяет условию однородности, т.е. для любого kсправедливо соотношение

то порядок уравнения можно понизить с помощью подстановки

После нахождения функции z(x) исходная функцияy(x) находится интегрированием по формуле

где C2− постоянная интегрирования.

Случай 7. Функция F(x, y, y', y'') является точной производной

Если удается найти такую функцию Ф(x, y, y'), не содержащую второй производнойy''и удовлетворяющую равенству

то решение исходного уравнения представляется интегралом

Таким образом уравнение второго порядка можно привести к уравнению первого порядка.  В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель.

studfiles.net

Определение типа дифференциальных уравнений и их решение. Система линейных неоднородных дифференциальных уравнений

Министерство Образования и Науки РФ

Новосибирский Государственный Технический Университет

Типовой расчёт по дисциплине

“дифференциальные уравнения”

Вариант 22

Факультет ПМИ

Группа ПМ-54

Студент: Чебукина С.В.

Преподаватель:

г.Новосибирск

2007г.

I. Определить тип и решить дифференциальные уравнения: 28, 35, 38 ,43

35. 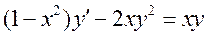 -  уравнение Бернули.

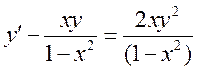
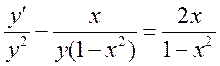
Что бы решить это дифференциальное уравнение, сделаем замену

тогда 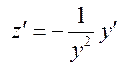, и

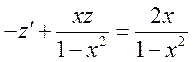
А такое дифференциальное уравнение решаем как однородное:

1.

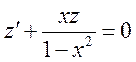
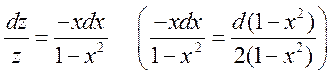
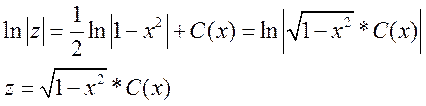
2.

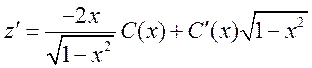
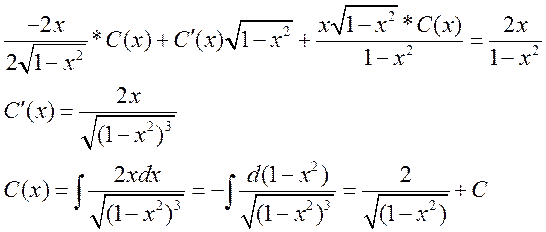
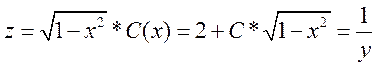
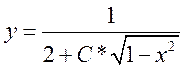
Ответ: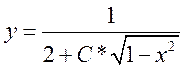

43. 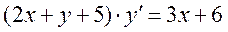 - однородное уравнение

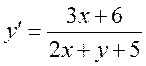
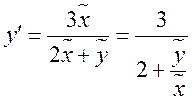
Делаем замену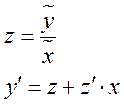

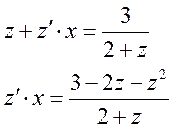
решаем последнее уравнение, как уравнение с разделяющими переменными.

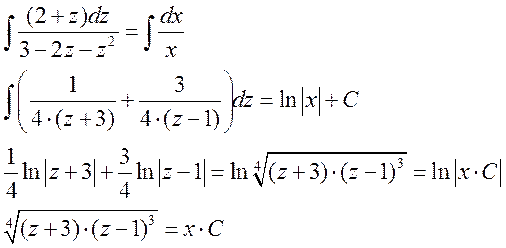
вспомним, что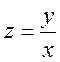

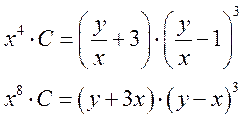
Ответ: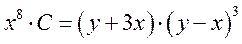

II. Рушить систему линейных неоднородных дифференциальных уравнений вида

                                       

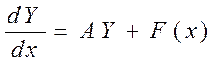
1. методом вариации постоянных.

найдем собственные значения матрицы А

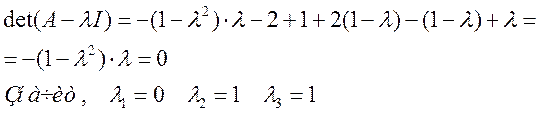
для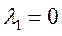

Значит, будет 1собственный вектор .

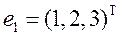
для

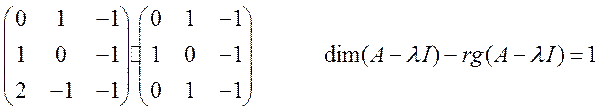
Значит, будет 1собственный вектор и 1 присоединенный вектор.

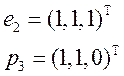
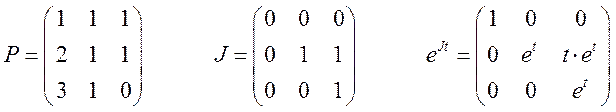
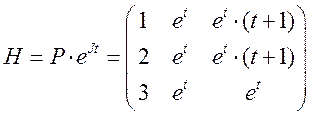
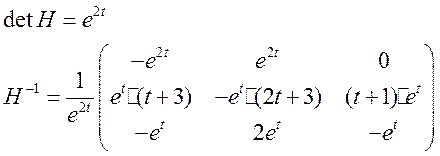
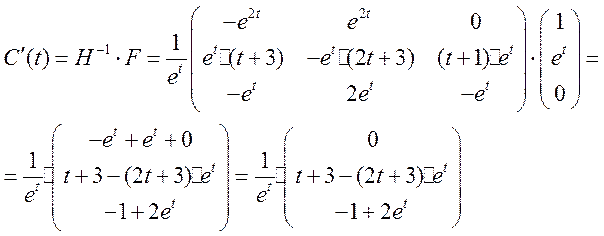
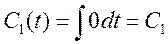
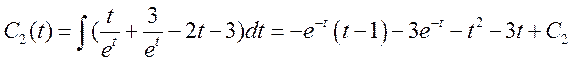
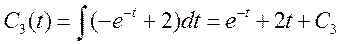
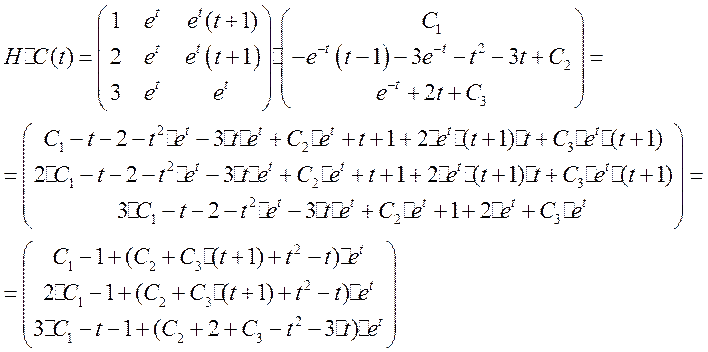
Ответ :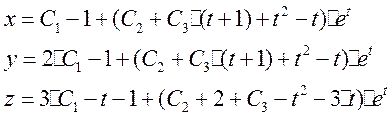  

 III. Решить неоднородное дифференциальное уравнение N-го порядка методом вариации постоянных.

20.   

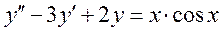
Решение однородного уравнения 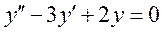 ищем в виде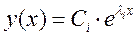

Характеристическое уравнение 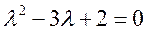 имеет корни

Общее решение однородного уравнения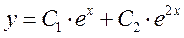

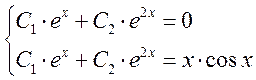
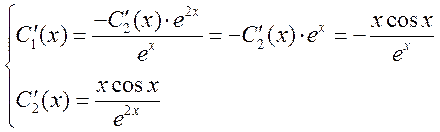
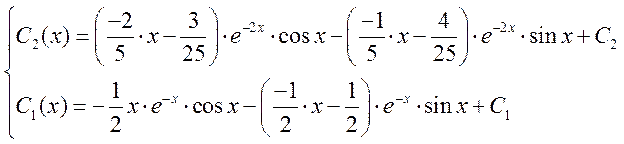
Ответ:

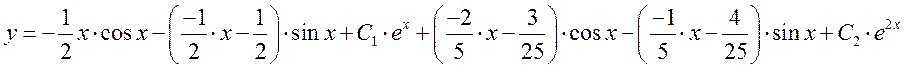
5.  

Характеристическое уравнение 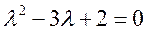 имеет корни

Общее решение однородного уравнения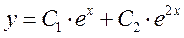

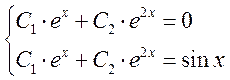
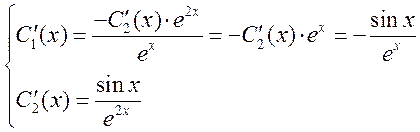
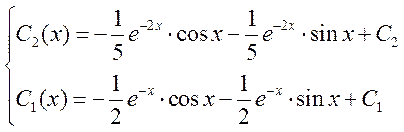
Ответ: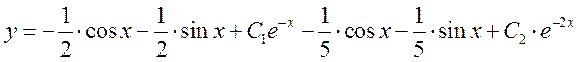  

vunivere.ru

Дифференциальные уравнения первого порядка

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Как решать дифференциальные уравнения первого порядка

Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:.Разделив это уравнение на , при , мы получим уравнение вида:,где .

Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:.

Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :.Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.

Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:,то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:.

Если и это не помогает, то пытаемся найти интегрирующий множитель.

Уравнения с разделяющимися переменными

;.Делим на и интегрируем. При получаем:.Подробнее >>>

Уравнения, приводящиеся к уравнениям с разделяющимися переменными

Делаем подстановку . Тогда;.Далее разделяем переменные и интегрируем.Подробнее >>>

Однородные уравнения

Решаем подстановкой:,где – функция от . Тогда;.Разделяем переменные и интегрируем.Подробнее >>>

Уравнения, приводящиеся к однородным

Вводим переменные и :;.Постоянные и выбираем так, чтобы свободные члены обратились в нуль:;.В результате получаем однородное уравнение в переменных и .Подробнее >>>

Обобщенные однородные уравнения

Делаем подстановку . Получаем однородное уравнение в переменных и .Подробнее >>>

Линейные дифференциальные уравнения

Есть три метода решения линейных уравнений.

1) Метод интегрирующего множителя.Умножаем уравнение на интегрирующий множитель :;.Далее интегрируем.Подробнее >>>

2) Метод Бернулли.Ищем решение в виде произведения двух функций и от переменной :.;.Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:.Определив , получаем уравнение с разделяющимися переменными для .Подробнее >>>

3) Метод вариации постоянной (Лагранжа).Здесь мы сначала решаем однородное уравнение:Общее решение однородного уравнения имеет вид:,где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :.Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .Подробнее >>>

Уравнения Бернулли

Подстановкой уравнение Бернулли приводится к линейному уравнению.

Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :.Подставляем в исходное уравнение:;.В качестве выбираем любое не нулевое решение уравнения:.Определив , получаем уравнение с разделяющимися переменными для .

Подробнее >>>

Уравнения Риккати

Оно не решается в общем виде. Подстановкойуравнение Риккати приводится к виду:,где – постоянная;   ;   .Далее, подстановкой:оно приводится к виду:,где .

Свойства уравнения Риккати и некоторые частные случаи его решения представлены на страницеДифференциальное уравнение Риккати >>>

Уравнения Якоби

Решается подстановкой:.Подробнее >>>

Уравнения в полных дифференциалах

При условии.При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:.Тогда.Отсюда получаем интеграл дифференциального уравнения:.

Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:;;;.Подробнее >>>

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция, при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.Подробнее >>>

Уравнения, не решенные относительно производной y'

Уравнения, допускающие решение относительно производной y'

Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, допускающие разложение на множители

Если удастся уравнение разложить на множители:,то задача сводится к последовательному решению более простых уравнений:;;;Подробнее >>>

Уравнения, не содержащие x и y

Здесь – постоянная:,где – корень уравнения.Подробнее >>>

Уравнения, не содержащие x или y

  или   Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда   или   .Далее интегрируем уравнение:;.В результате получаем выражение второй переменной через параметр .

Более общие уравнения:   или   также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .Чтобы выразить вторую переменную через параметр , интегрируем уравнение:;.Подробнее >>>

Уравнения, разрешенные относительно y

Уравнения Клеро

Такое уравнение имеет общее решениеПодробнее >>>

Уравнения Лагранжа

Решение ищем в параметрическом виде. Полагаем , где – параметр.Подробнее >>>

Уравнения, приводящиеся к уравнению Бернулли

Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .Подробнее >>>

Использованная литература:В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 20-05-2016

1cov-edu.ru

Дифференциальные уравнения без x или y

Здесь мы рассматриваем метод решения уравнений вида:(1)   ;(2)   .То есть это дифференциальные уравнения первого порядка, не разрешенные относительно производной, и которые не содержат одну из переменных в явном виде.

Общий метод решения

Решение таких уравнений мы ищем в параметрическом виде. Пусть – параметр. Тогда переменные и являются функциями от этого параметра :;.Производная также является функцией от параметра :.

Преимущество параметрического представления заключается в том, что его можно создать многими способами. В качестве примера рассмотрим функцию.В параметрическом виде ее можно представить так:.Или так:.То есть мы можем найти бесконечно много способов, чтобы создать параметрическое представление для одной и той же функции.

Мы будем использовать это преимущество параметрического представления при решении уравнений (1) и (2). Общий метод заключается в том, чтобы подобрать такую функцию , чтобы уравнения (1) или (2) можно было разрешить относительно переменной или .

Рассмотрим уравнение (1):(1)   .Пусть мы подобрали такую функцию , что при подстановке в (1), уравнение (1) удалось разрешить относительно . То есть мы получили параметрическое представление для переменной :.Тогда имея две функции и , мы можем найти . Для этого запишем дифференциал:.Интегрируя, получаем параметрическое представление для :.

Теперь рассмотрим уравнение (2):(2)   .Пусть мы подобрали такую функцию , что при подстановке в (2), уравнение (2) удалось разрешить относительно . То есть мы получили параметрическое представление для переменной :.Тогда имея две функции и , мы можем найти . Для этого запишем дифференциал:.Интегрируя, получаем параметрическое представление для :.

Уравнения, разрешенные относительно переменной

Рассмотрим наиболее простой случай, когда исходное уравнение(1)   удается разрешить относительно переменной :.В этом случае проще положить . Тогда .

Тогда имея две функции и , мы можем найти :;.

Аналогично, если исходное уравнение(2)   удается разрешить относительно переменной :.То положим . Тогда .

Имея две функции и , мы можем найти :;.

Пример

Решить уравнение:(1.1)  

Решение

Это дифференциальное уравнение первого порядка, не разрешенное относительно производной. Оно не содержит переменную в явном виде. Ищем решение в параметрическом виде, введя параметр . Это уравнение разрешено относительно переменной . Поэтому делаем подстановку:(1.2)   .Тогда(1.3)   .

Итак, мы выразили переменную через параметр . Теперь осталось выразить через параметр переменную . Для этого запишем дифференциал переменной :.Отсюда получаем дифференциал переменной :(1.4)   .Распишем дифференциал , используя (1.3):;(1.5)   .Подставляем (1.2) и (1.5) в (1.4):.Интегрируем:.

Итак, мы получили решение в параметрическом виде:(1.6)   ;(1.3)   .

Далее мы можем явно выразить y через x. Для этого перепишем уравнение (1.6):.Решаем квадратное уравнение:.Заменим постоянную ::.Подставляем в (1.3):

Ответ

.

Уравнения, не разрешенные относительно переменной

Теперь рассмотрим более общий случай. Рассмотрим уравнение (1):(1)   .Если это уравнение не удается разрешить относительно переменной , то у нас нет гарантий, что мы можем получить решение. Но мы можем попытаться найти такую функцию, чтобы подставив в (1), можно было выразить переменную через параметр . Если это удастся сделать, то у нас будут две функции, зависящие от параметра :;.Подставляя их в выражение для дифференциалаи интегрируя, мы найдем .

Аналогично поступаем для уравнения (2):(2)   .Нашей задачей является найти такую функцию, чтобы подставив в (2), можно было выразить переменную через параметр . Если это удастся сделать, то у нас будут две функции, зависящие от параметра :;.Подставляя их в выражение для дифференциалаи интегрируя, мы найдем .

Пример

Решить уравнение:(2.1)   .

Решение

Это дифференциальное уравнение первого порядка, не разрешенное относительно производной. Оно не содержит переменную в явном виде. Ищем решение в параметрическом виде. Нашей задачей является найти такую подстановку , чтобы из уравнения (2.1) можно было выразить переменную через параметр .

Можно увидеть, что такой подстановкой является(2.2)   .Подставляем в исходное уравнение (2.1):;;;(2.3)   .

Итак, мы выразили переменную через параметр . Теперь осталось выразить через параметр переменную . Для этого запишем дифференциал переменной и выразим его через параметр ..Подставим (2.2):.Здесь – функция от , определяемая из (2.3).Интегрируем по частям и подставляем (2.3):;;.

Ответ

;.

Автор: Олег Одинцов.     Опубликовано: 22-08-2012   Изменено: 01-04-2016

1cov-edu.ru

Как определить тип дифференциального уравнения

В математике существует множество различных типов уравнений. Среди дифференциальных также различают несколько подвидов. Отличить их можно по ряду существенных признаков, характерных для той или иной группы.

Вам понадобится

Инструкция

completerepair.ru